基于主元增广矩阵的SVM故障检测

郭金玉，李 涛，李 元

沈阳化工大学信息工程学院，辽宁沈阳110142

现代工业生产高度智能化，对复杂工业过程而言，有效提高控制系统的故障检测性能变得尤为重要．近年来，基于数据驱动的多元统计分析方法被深入研究和应用，并在工业过程领域取得了快速发展[1-4]．该方法只需在实际工业生产过程中获取历史数据，再通过数据建立监测模型，从而实现工业过程的故障检测，过程中不需要依赖先验知识和数学模型，因此备受关注．

主元分析(principal component analysis, PCA)是工业过程中故障诊断和检测的典型算法，已被广泛用于多种场景[5-6]．PCA算法是一种线性降维的方法，它将过程数据投影到低维空间，保留主要变量，实现降维目的，主要针对相关过程中因变量引起的共线性问题．在主元子空间和残差子空间中，该算法使用平方预测误差(squared prediction error, SPE)和Hotelling’sT2指标对样本状态进行监控[7]．由于PCA算法处理的数据需满足高斯分布的假设前提，对非线性工业过程的故障检测效果不佳．为此，SHIOKAWA等[8-10]提出核主元分析(kernel principal component analysis, KPCA)算法，但由于KPCA算法是用SPE和Hotelling’sT2指标监控过程变量，而这2个指标需要数据服从多元高斯分布且样本间相互独立，导致它们的故障检测效果较差．在现代工业生产过程中，变量之间常存在较强的非高斯特性和样本自相关性，很大程度上影响了故障检测的性能．

支持向量机(support vector machine, SVM)因有强大的泛化能力和解决各种分类问题等优势，被广泛研究学习[11-12]．采用SVM对数据进行故障检测时，需同时使用正常数据和故障数据来训练模型，学习两种数据的特征变化．针对高维数据，GUYON等[13]提出支持向量机递归特征消除(support vector machine recursive feature elimination, SVM-RFE)算法．SHIEH等[14]通过使用总体排序或特定类型的排序来选择关键特征，提高线性SVM-RFE对样本特征的提取．但由于故障检测与诊断并不只是线性问题，XUE等[15]用高斯核SVM-RFE提取非线性特征进行故障检测与诊断，该方法关键是核参数的选择，通过对比选择出最优参数，建立一种先进的故障检测与诊断框架．针对非线性过程中SVM检测性能不足的问题，ZHANG等[16]结合核独立元分析(kernel independent component analysis, KICA)、KPCA和SVM的优点，开发了一种非线性动态故障检测方法．

对于高维数据，SVM的运行时间较长．为减少SVM的运行时间，需对数据进行特征提取和降维．但是，SVM算法性能的优异依赖数据特征提取的能力．传统的PCA算法对数据进行特征提取和降维，获得的主元和残差中仍具有较强的自相关性，这会降低Hotelling’sT2和SPE控制图的故障检测性能．为减少SVM的运行时间，本研究运用时滞和时差特性降低样本自相关性，减少分类过程中类别与附加维度的重叠，提高SVM的故障检测性能，提出一种基于主元增广矩阵的SVM(SVM based on principal component augmented matrix, PCAM-SVM)故障检测方法．通过建立PCA模型提取数据的得分矩阵，对得分引入时差和时滞输入特性，将3者组合成增广矩阵作为SVM的输入，再运用SVM模型对数据进行故障检测．该方法考虑到了样本的空间和时间分布情况，通过引入时滞和时差输入特性，有效降低了样本间的自相关性，减少了分类过程中类别与附加维度的重叠，提高了SVM算法的故障检测性能．

1 PCAM-SVM故障检测

1.1 SVM

SVM[11-12]作为机器学习中的经典分类算法，在处理小规模数据集和非线性问题上有许多优点．对线性数据，SVM能够建立最大分离超平面对数据进行分类；对非线性问题，需先将数据投影到高维空间，去除数据非线性再建立最大分离超平面，使数据被有效分类．由于分离平面是基于支持向量构造的，所以SVM是一种很好的解决高维问题的方案．

假设样本训练集为H={(x1,y1),(x2,y2),…,(xm,ym)}， 样本类别yi∈{-1, 1}， 在样本空间中需要找到一个最大分离超平面，将样本划分为不同类别．SVM对指定数据分类的超平面(w,b)满足

wTx+b=0

(1)

其中， 权重向量w=(w1,w2, …,wm)Т；b为位移项；xi为样本空间中任意点．若(w,b)能够将样本正确分类，则对于(xi,yi)∈H， 有

(2)

距离超平面最近的样本点使式(2)成立，此类样本点即为支持向量．两个异类支持向量到超平面的距离之和为间隔γ． 为找到最大间隔的超平面，实现最大程度分类，需找到满足式(2)的参数w和b， 即SVM的基本型为

(3)

考虑到一些无法分类的样本，以及SVM在一些样本上可能分类错误，引入惩罚因子C和松弛变量ξi， 则式(3)可改写为

(4)

其中，ξi≥0，C>0．

将式(4)转化为对偶问题，使用拉格朗日乘数法求解，则该问题的拉格朗日函数为

(5)

其中，拉格朗日乘子αi≥0，μi≥0，α=(α1,α2, …,αm)，μ=(μ1,μ2, …,μm)．

令L(w,b,α,ξi,μ)对w、b和ξi的偏导为0，可得

(6)

(7)

C=αi+μi

(8)

对式(4)求解，得到模型

(9)

假设样本为非线性数据，为更好地实现分类，通过非线性映射φ(x)将数据投影到高维空间．为避免高维运算，引入核函数

K(xi,xj)=[φ(xi),φ(xj)]=

[φ(xi)]Tφ(xj)

(10)

则通过核函数计算后模型(9)变为

(11)

因此，无论是在对线性还是非线性数据进行分类时，SVM都可将其有效转化，实现对数据高效准确地分类．

1.2 基于主元增广矩阵的SVM算法

在多元统计分析中，PCA能够达到降维并提取原始数据主要特征的目的．假设随机变量xi的样本集表示为X=[x1,x2, …,xm]，m为样本数，xi∈Rn(i=1, 2, …,m)， 则定义标准化后X的协方差矩阵为

(12)

对S进行特征值分解，计算特征值和特征向量，并按照特征值降序排列，再求取主元个数z． 现有的选择主元得分个数的方法包括累计方差贡献率(cumulative percent variance, CPV)、碎石检验、平行分析和重建误差准则等方法，何种方法最佳，目前尚未达成共识．由于当CPV≥85%时，所获得的主元能够代表样本的主要特征[17-18]，因此，本研究采用CPV方法．CPV的计算式为

(13)

其中，λi为协方差矩阵的特征根．由前z个特征向量构成的矩阵就是负载矩阵P， 则得分矩阵为

T=XP

(14)

在动态主元分析(dynamic principal component analysis, DPCA)中，KU等[19]通过引入时滞特性实现了对过程静态信息和动态信息的同步提取，提高了故障检测性能．CHIANG等[20]指出，用时滞特性解决样本自相关性的思想在分类问题中能够减少类别与附加维度的重叠，只要数据充足并且增加维度合理，引入时滞特性就会带来良好的检测结果．ZHANG等[21]运用时差思想，通过建立不同的统计信息，消除了样本非线性对故障检测的影响，提高了工业过程的故障检测性能．本研究通过同时引入得分矩阵的时滞和时差特性来提升SVM算法的性能．

由式(14)可得正常数据在时刻t的得分Tn(t)， 然后构造时滞输入特性Tn(t-1)和时差输入特性Tn(t)-Tn(t-1)， 并组合成增广矩阵

Tnormal=[Tn(t),Tn(t-1),Tn(t)-Tn(t-1)]

(15)

在故障操作条件下获取故障数据，同样通过PCA模型计算得分矩阵为Tf， 在主元空间中构造出故障数据的增广矩阵为

Tfault=[Tf(t),Tf(t-1),Tf(t)-Tf(t-1)]

(16)

将Tnormal与Tfault作为SVM模型的训练数据，即Ttrain=[Tnormal,Tfault]， 对SVM训练后获得判别分类函数．建立模型后，SVM能学习正常和故障数据的特性，进而对数据正确分类．将测试数据输入模型，通过超平面划分，将正常数据划分成一类并标记为0，故障数据划分成另一类并标记为1．

1.3 基于主元增广矩阵的SVM故障检测

PCAM-SVM方法故障检测流程如图1．该方法主要包括离线模型建立和在线故障检测两个步骤．

图1 PCAM-SVM方法故障检测流程图Fig.1 Flow chart of fault detection method using PCAM-SVM

离线模型建立具体步骤为：

1)采集正常操作条件下的数据集X1和故障操作条件下的数据集X2；

2)通过PCA建模在主元子空间分别计算正常和故障数据的得分矩阵Tn和Tf；

3)在时刻t的Tn(t)和Tf(t)中分别加入时滞输入特性和时差输入特性，并根据式(15)和(16)生成增广矩阵Tnormal和Tfault；

4)生成SVM训练数据集Ttrain并对Ttrain贴标签，正常数据标记为0，故障数据标记为1；

5)用Ttrain训练SVM模型,获得判别分类函数．

在线故障检测具体步骤为：

1)利用离线建模数据的均值和方差，对测试数据集xtest进行标准化；

2)将标准化后的测试数据投影到PCA模型上，采用式(14)计算得分矩阵Tt；

3)在时刻t的Tt(t)中加入时滞和时差输入特性生成测试数据集的增广矩阵

Ttest′=[Tt(t),Tt(t-1),Tt(t)-Tt(t-1)]

(17)

即SVM模型的测试数据集；

4)将测试数据集的主元增广矩阵Ttest′送入SVM模型进行分类，正常数据标记为0，故障数据标记为1．

2 仿真结果与分析

2.1 多变量动态过程数值仿真

根据文献[22]构造一个具有5个变量E(t)、Y(t)、V(t)、U(t)和W(t)的动态过程，对应的数值模型为

(18)

Y(t)=Z(t)+V(t)

(19)

其中，V(t)为均值为0、标准差为0.01的正态分布的噪声序列； 输入U(t)为

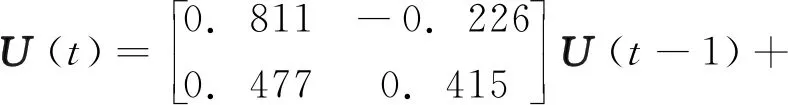
(20)

其中，W(t)是服从[-2，2]的均匀分布．当t=1时，设U(0)=[0 0]T，W(0)=[-1 1]T， 则由过程相关输入U(t)和输出Y(t)共同组成监控数据集．为验证PCAM-SVM的有效性，由上述模型生成1 000个正常样本，并引入两种类型的故障：① 对W(t)增加幅值在[0.1 -0.7]内的阶跃，产生400个阶跃故障；② 对W(t)增加斜坡信号为0.003×(i-1 400)的扰动(i为采样时刻)，产生400个斜坡故障．其中，斜坡信号斜率的变化范围是[0.000 8 -0.005 0]．

采用SVM、PCA-SVM和PCAM-SVM三种方法对不同幅值阶跃故障条件下的故障检测率进行仿真，结果如图2．由图2可见，在不同幅值情况下，PCAM-SVM方法的故障检测率最高．

图2 不同幅值的阶跃故障检测率Fig.2 Detection rates against step changed sizes

改变斜坡故障信号的斜率值，分别计算3种方法的检测率，结果如图3．由图3可见，在不同斜率的斜坡故障情况下， PCAM-SVM方法的故障检测率仍然最优．

图3 不同斜率的斜坡故障检测率Fig.3 Detection rates against slope sizes

值得注意的是，本例中斜坡故障信号的斜率范围较小，属于微小型故障，一般算法在故障特征提取上具有一定难度．PCAM-SVM方法通过引入时滞和时差输入特性来构建主元增广矩阵，增加了模型输入复杂度，减少分类过程中类别与附加维度的重叠，降低了样本间的自相关性，能有效提取数据的特征，提高SVM的检测效果．

图4为PCA-SVM主元得分和PCAM-SVM主元增广矩阵自相关性．由图4可见，PCAM-SVM方法在主元空间中通过时滞和时差输入特性构造的增广矩阵能有效地降低样本间的自相关性．

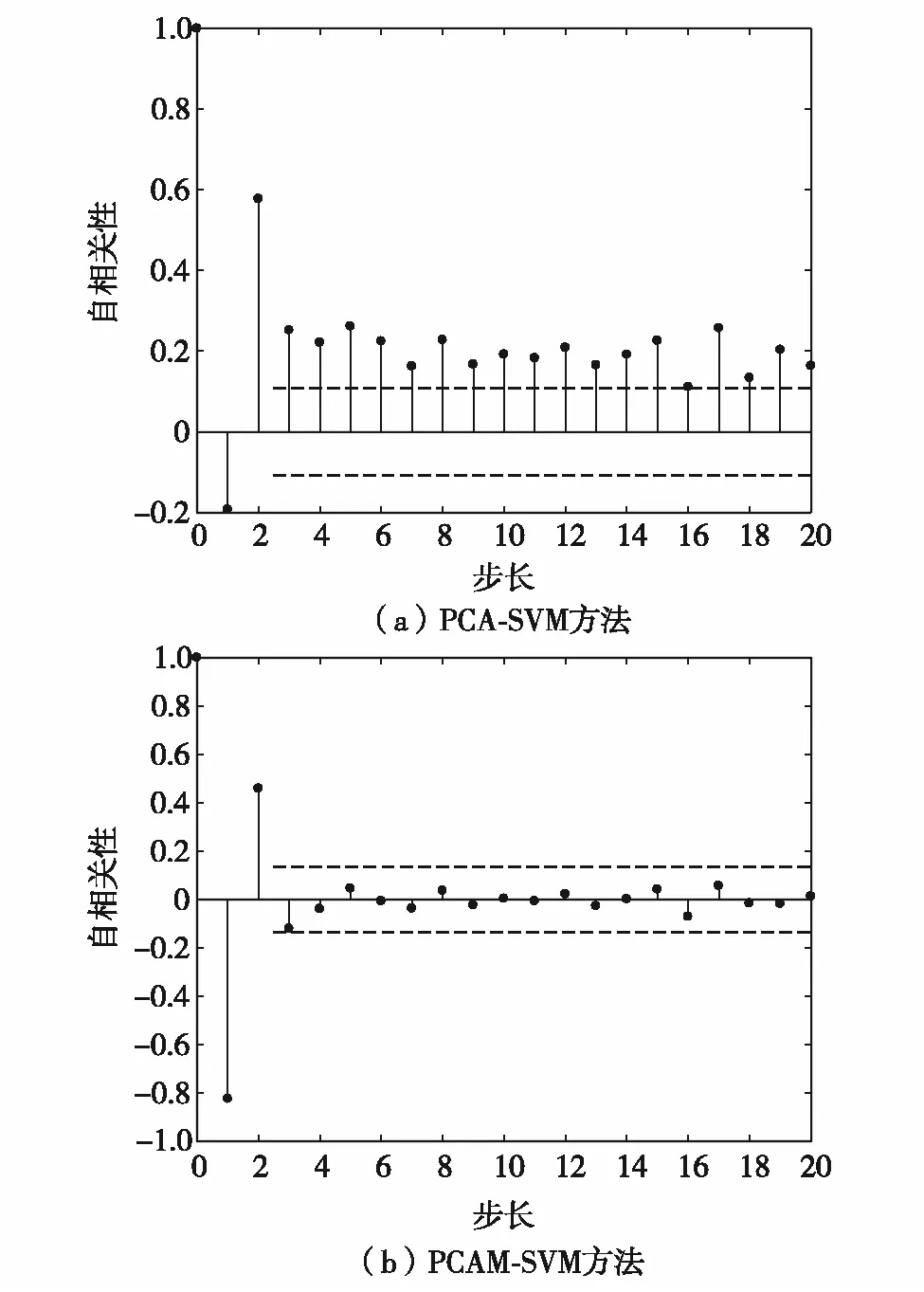
图4 PCA-SVM和PCAM-SVM方法的自相关性Fig.4 Autocorrelation of PCA-SVM and PCAM-SVM

2.2 TE过程仿真

田纳西-伊斯曼(Tennessee-Esatman, TE)过程是国际通用的模拟实际工业过程的仿真平台[23-24]，被广泛应用于过程监控领域．TE过程包括5个主要操作单元、4种气体进料、2个气液放热反应生成的2种主产品和2个衍生放热反应生成的2种副产品等，过程工艺复杂，涉及变量较多．TE过程具体的模型流程图如图5．其中，1～13表示13个检测点，每个检测点包含1个或多个变量传感器，用于数据采集．将TE过程产生的数据集用于仿真测试，该数据集是在TE仿真器中持续运行48 h获得，包含流量、压力、温度和液位等52个观测变量(41个测量变量和11个控制变量)，采样频率为3 min．

训练数据集包含正常样本和故障样本各500个，测试数据集包含160个故障样本．分别对训练集的正常样本和故障样本进行主元分析，获取对应的得分矩阵，然后进行时滞和时差操作并将数据进行组合， 再将相应的主元增广矩阵用于SVM模型训练．本研究通过寻优测试设置惩罚因子C=0.15， 窗宽g=0.45． 对PCA、ICA、KPCA、PCA-SVM和PCAM-SVM算法中主元和独立元个数的选取，采用85% CPV来确定，具体设置如表1．

图5 TE过程模型流程图Fig.5 Flow chart of TE process model

表2是6种故障检测方法对不同故障类型的检测率结果．由表2可见，使用PCAM-SVM算法，故障1、3、4、5、8、9、10、11、14、15、16、17、19、20和21的检测率，比其他检测方法都有不同程度的提高，平均故障检测率为99.49%，验证了该方法的有效性．

表1 五种故障检测方法的主元和独立元数量Table 1 Numbers of principal components and independentcomponents for five fault detection methods 个

表2 6种算法对TE过程故障检测率

(续表2)

结 语

提出一种基于主元增广矩阵的SVM故障检测方法，通过PCA提取得分矩阵，引入其时滞输入特性和时差输入特性，有效去除过程变量之间的自相关性，将3者组合成增广矩阵作为SVM的输入，运用SVM进行故障检测．将PCAM-SVM方法应用到多变量动态过程数值例子和实际的TE过程中，结果表明，与PCA、ICA、KPCA、SVM和PCA-SVM方法相比，PCAM-SVM方法有效提高了故障检测率．