多电飞机270 V高压直流电力系统小信号稳定性分析
2021-09-23刘勇智于锦禄陈俊柏
刘勇智, 聂 恺, 于锦禄, 陈俊柏
(1.空军工程大学航空工程学院, 西安, 710038; 2.空军工程大学研究生院, 西安, 710051)
为了解决传统飞机运行成本高、可靠性和稳定性较差的问题,多电飞机[1]的概念相继被提出。相比于传统飞机,多电飞机广泛使用电能来代替气压能和液压能,主要有两大优势:一方面随着大量的机电作动器和功率电传技术被应用,飞机的运行更加稳定,并且有效简化了系统的复杂性。另一方面,由于减少了传统液压管道,多电飞机的体积得以减小,与此同时又使燃油效率得到提升。在飞机上,与其他二次能源相比较而言,电能的优势尤其突出,可靠性大大增强。当飞机发生故障时,电能驱动的系统往往可以仅将故障点隔离出来,而传统的气、液压能一般会将整个系统电路全部进行隔离,使系统不能正常运作。除此之外,使用电能时,在相同状况下,故障发生的可能性仅是传统气、液压能系统的百分之一。但是,含有大量电力电子变换器件的系统中往往表现为恒功率负载的特性,使系统阻尼减小,更容易发生振荡,此时电力系统平稳运行尤为关键,小扰动稳定性问题成为研究重点。
飞机电力系统小信号模型建模方法[2-4]通常有3种:状态空间平均法(SSA)dq变换法和平均值建模法。相比于其他两种方法,dq变换法在飞机电力系统动态建模上具有突出优势[5-6],构建的状态方程阶数较少。文献[7]运用电压、电流双闭环反馈对电机进行控制,文献[8]提出了一种用于多电飞机电力系统的自耦变压器整流装置(ATRU)的动态模型。该模型大大降低了飞机动力系统建模的复杂性,使其在对电力系统进行暂态和稳定分析时更加实用。目前研究电力系统稳定性分析方法有阻抗分析法,李雅普诺夫稳定性判据等[9-11]。文献[12]提出了一种基于模块的小信号建模方法,为复杂多电飞机电力系统建模提供了新的思路。
对电力系统稳定性起到主要作用的参数往往难以选取,需要进行大量的筛选工作。利用参与因子可以很好地解决这一问题,故本文在建立飞机电力系统小信号模型的基础上,通过对其线性化得到系统特征值,并将参与因子与系统特征值结合[13-14],显示了各模态的参与因子与状态变量的关系,可以直观、快捷地找出主要参与因子,简化系统稳定性分析的过程。
1 系统小信号模型
本文研究的飞机电力系统概念图如图1所示。
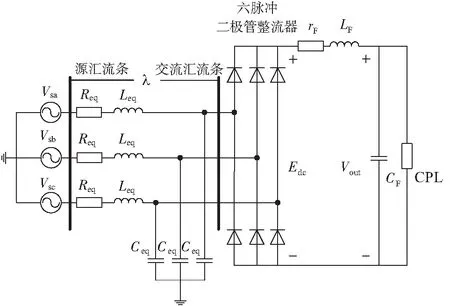
图1 飞机电力系统概念图
Req、Leq、Ceq分别是传输线上的等效电阻、电感、电容。CPL为恒功率负载。rF、LF、CF代表系统直流部分滤波器相应参数。
本文采用dq建模法,建立适合分析系统小信号稳定性的模型。
1.1 电力系统dq等效电路
飞机电力系统的数学模型建模方法主要有3种:dq变换法、平均值建模法和状态空间平均建模法。相比于其他两种方法dq变换法建立的模型可以使系统中各个部分很好地连接在一起。同时,dq变换法建立的电力系统数学模型具有更低的阶数,利于分析。因此,本文采用dq变换法对飞机电力系统进行建模。
图1对应的dq坐标系下的等效电路如图2所示。

图2 飞机电力系统等效电路
1.2 非线性动态模型和线性化模型
将基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)应用于图2的电路中,得到一组非线性微分方程。
状态变量:x=[IdsIqsVbus,dVbus,qIdcVout]
输入量:u=[VmPCPL]
输出量:y=[Vout]
系统非线性微分方程为:
(1)
假设飞机电力系统在正常运行状态下工作点不发生快速变化。因此,利用泰勒展开的一阶项对式(1)进行线性化处理,从而得到一组围绕平衡点的线性微分方程,则式(1)的dq线性化模型为:
(2)
其中:
(3)
(4)
(5)
由式(4)可知,线性化模型需要定义Vout,o、λo用于小信号仿真和稳定性分析研究。建立出电力系统单线图,得到潮流方程[15],通过牛顿-拉夫逊迭代法可以求得稳态点数据Vout,o、λo,系统中参数如表1所示。

表1 飞机电力系统参数
2 系统稳定性分析
2.1 系统特征值分析
由特征值理论可知:当求得的系统特征值全部处于坐标轴左侧时,此时所研究的飞机电力系统是稳定的;当求得的系统特征值存在于任一处坐标轴右侧时,所研究的飞机电力系统不稳定。已知电力系统小信号数学模型,由式(4)中的雅可比矩阵A(x0,u0)计算出特征值λ=δ±jω。
当特征值实部δ小于0,该系统处于稳定状态;当特征值实部δ大于0,该系统处于不稳定的振荡状态;当特征值实部δ等于0,该系统处于临界状态,即不稳定。将此系统用特征值法进行分析,可以快速、直观地观察系统的稳定性,并且整个计算过程简便,准确度高。经过计算,可得系统特征值分布如图3所示。

图3 系统特征值分布图
PCPL从0~30 kW变化时系统在不同功率下的特征值如图4所示。

图4 不同功率下的特征值(λ5,λ6)
图4中选取靠近坐标轴的局部特征值,随着PCPL的增大,该电力系统特征值λ5和λ6(分别位于图4的上半部和下半部)的实部由坐标轴负半轴逐渐过渡到正半轴,这也就表示系统的稳定性在逐渐变差。当PCPL=17 kW到PCPL=18 kW时,系统特征值开始越过坐标轴,系统失稳,即此时系统处于稳定性的临界点。
在0、0.4、0.6、0.9 s分别给定功率7、12、17、18 kW如图5所示。
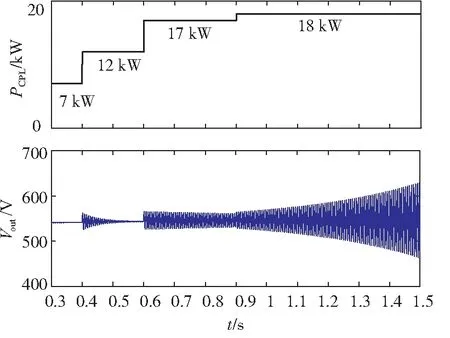
图5 负载功率改变时电压的变化情况
由图5可知,PCPL变化对输出电压的影响如下:当给定的功率逐渐增大,系统输出电压收敛到稳定的能力逐渐变差。给定功率为17 kW时,系统输出电压有收敛到稳定的趋势,当给定功率增加到18 kW时系统输出电压无法收敛,呈现发散趋势。该仿真验证了在18 kW恒功率负载值下发生失稳时的理论结果。这大于不稳定状态下的17 kW值。
2.2 特征值所对应模态参与因子分析
当系统受到小扰动后,系统的稳定性对每一个状态变量的反应程度均不同,采用参与因子来表示这种影响程度,设特征值的左、右特征向量矩阵分别为Ψ=(φ1T,φ2T,φ3T…)和Φ=(φ1,φ2,φ3…),Λ=diag(λ1,λ2,λ3…)表示所有特征值组成的对角矩阵。因而有如下关系式[16]:

(6)
参与因子pki可以由第k个状态变量对第i个特征值的相关性表示:
pki=φikφki
(7)
式中:φki和φik为矩阵Φ和Ψ中相应行和列的元素。
由图3特征值分布可知,其相对应的各模态参与因子与状态变量之间的关系如表2所示。

表2 各模态参与因子与状态变量
表2所示状态变量Vbus,d是模态λ1、λ2对应的主要参与因子;状态变量Vbus,q是模态λ3、λ4对应的主要参与因子;状态变量Vout是模态λ5、λ6对应的主要参与因子。
3 系统参数变化对系统稳定性影响
电力系统矩阵的特征值会根据参数值的变化而变化,特征根离虚轴的距离决定了其系统的稳定性。靠近虚轴的特征根称为主导特征根。由图3可选取此系统的主导特征根λ5、λ6。
本文选取了电力系统中具有代表性的参数:直流侧滤波器电容CF、直流侧滤波器电感LF、系统的频率ω。
在保证系统其他参数不变的前提下,分别给定系统直流侧滤波器电容CF的值为300、350、400、450、500、550、600、650 μF。得到电力系统直流侧滤波器电容CF增大时系统主导特征值λ5、λ6的变化轨迹如图6,其中300 μF≤CF≤650 μF。
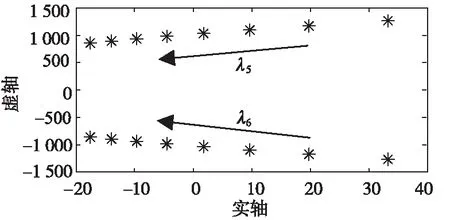
图6 CF增大时特征根变化趋势
由图6可知:随着CF的增大,λ5、λ6由坐标轴右侧逐渐移到坐标轴左侧,意味着实部由正数变为负数,整个系统由不稳定状态过渡到稳定状态,并且稳定性增强。此外通过表2可知Vout是模态λ5、λ6的主要参与因子,随着CF的增大,Vout的稳定性也随之增强。
在0.4、0.6、0.8、1.0 s时分别在系统中给定功率12、18、26、32 kW。并选取CF的值分别为300、500、700、900 μF如图7所示。
由图7可知,随着CF值的增大,相同条件下系统可承受负载越来越大,直流侧输出电压Vout收敛到稳定所需时间缩短。意味着CF越大,系统稳定性越好,同时可以准确的预估出CF的失稳点。由此可见,CF的值越大,系统失稳发生的概率越小。

图7 CF变化时系统的带载能力
在保证系统其他参数不变的前提下,分别给定系统直流侧滤波器电感LF的值为1、1.5、2、2.5、3、3.5、4、4.5、5 mH。得到电力系统直流侧滤波器电感LF增大时系统主导特征值λ5、λ6的变化轨迹如图8,其中1 mH≤LF≤5 mH。
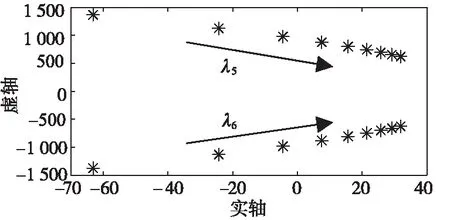
图8 LF增大时特征根变化趋势
由图8可知:随着LF的增大,λ5、λ6由坐标轴左侧逐渐移到坐标轴右侧,意味着实部由负数变为正数,整个系统由稳定状态过渡到不稳定状态。此外通过表2可知Vout是模态λ5、λ6的主要参与因子,随着LF的增大,Vout的稳定性也随之降低。
在保证系统其他参数不变的前提下,0.4、0.6、0.8、1.0 s时分别在系统中给定功率10、13、18、34 kW。并选取LF的值分别为1、2、3、4 mH如图9所示。
由图9可知,随着LF值的增大,相同条件下系统可承受负载越来越小,直流侧输出电压Vout收敛到稳定所需时间变长。意味着LF越大,系统稳定性越差,同时可以准确预估出LF的失稳点。由此可见,LF的值越大,系统失稳发生的概率越大。

图9 LF变化时系统的带载能力
在保证系统其他参数不变的前提下,分别给定系统频率ω的值为200、250、300、350、400、450、500、550、600 Hz。得到电力系统频率ω增大时系统主导特征值λ5、λ6的变化轨迹如图10,其中200 Hz≤ω≤800 Hz。
由图10可知,随着ω的增大,λ5、λ6由坐标轴右侧逐渐移到坐标轴左侧,意味着实部由正数变为负数,整个系统由不稳定状态过渡到稳定状态,并且稳定性增强。此外通过表2可知Vout是模态λ5、λ6的主要参与因子,随着ω的增大,Vout的稳定性也随之增强。

图10 系统频率增大时特征根变化趋势
在0.4、0.6、0.8、1.0 s时分别在系统中给定功率16、18、20、22 kW。并选取ω的值分别为200、400、600、800 Hz。带载能力如图11所示。

图11 频率变化时系统的带载能力
由图11可知,随着ω值的增大,相同条件下系统可承受负载越来越大,直流侧输出电压Vout收敛到稳定所需时间变短。意味着ω越大,系统稳定性越强,同时可以准确的预估出ω的失稳点。由此可见,ω的值越大,系统失稳发生的概率越小。
4 结语
本文针对飞机电力系统直流侧滤波器等参数对应系统的稳定域难以确定、参数主要参与因子选取困难的问题,提出了一种基于特征值及其参与因子分析系统稳定性的方法:通过对系统稳定点的分析,结合泰勒公式建立了飞机电力系统小信号模型,并运用特征值原理、参与因子原理分析系统的稳定性。此分析过程快速、便捷,并且分析结果具有高精度。通过与simulink仿真相结合,验证了模型的有效性和可行性。在分析过程中,通过对飞机电力系统中主要参数进行数值上改变,可以观察的系统稳定性的变化趋势,从而获取准确的稳定边界,结果表明:系统直流侧滤波器电容CF的值越大,系统越稳定。系统直流侧滤波器电感LF的值越小,系统越稳定。系统频率ω的值越大,系统越稳定。同时此方法为系统预测各参数失稳点提供了有效、快捷的解决办法。
