基于模糊控制的无人机集群视觉着降
2021-09-23吴贤宁梁晓龙张佳强任宝祥尹逢川
吴贤宁, 李 哲, 梁晓龙, 张佳强, 任宝祥, 尹逢川
(1.空军工程大学空管领航学院, 西安, 710051; 2.陕西省电子信息系统综合集成重点实验室, 西安, 710051)
随着国防技术不断取得新的进展,无人机在执行情报侦察与监视、攻防对抗等作战任务时所面临的情况越来越复杂,无人机集群作战的理念应运而生[1]。近年来,集群作战逐渐从理论走向工程实践,安全回收成为研究中的一个热点问题。自主着降是无人机安全回收的重要手段之一[2-3]。
目前,计算机视觉技术在无人机领域中飞速发展,无人机利用视觉信息进行目标检测,通过成像原理与投影关系进行目标定位已成为无人机导航的主要方式[4-6]。在实际环境中,如果采用GPS信号进行着降,由于GPS定位本身存在误差,且易受干扰,定位不稳定会导致无人机自主降落失误[7]。如果采用视觉方式着降,由于四旋翼无人机是一个四输入六输出的欠驱动、非线性、强耦合系统,易受风的干扰而影响其自身位置与姿态,导致与机体连接的视觉传感器存在测量误差[8]。另外,电机机械振动对视觉传感器的测量也存在一定干扰,电机转动速度越快,视觉传感器距离旋翼越近,振荡越剧烈[9]。在接近地面过程中,地面效应会对无人机产生空气动力干扰[10],这种非线性影响也是一个无法忽视的因素,常规PID控制难以达到有效的精度控制[11]。文献[12]在旋翼无人机的机载云台稳定控制中引入一个补偿控制器,提高了机载云台的稳定性。文献[13]分析了无人机姿态采集的误差,并引入互补滤波器消除误差。以上研究都是针对于单个无人机平台进行的推导与验证,关于无人机集群的自主着降鲜有人关注,目前在工程实践上,集群的自主回收大多是依靠人工降落,或者利用较宽阔的场地,使各无人机之间保持较大的安全距离。这样的方法会造成大量人力与场地的浪费,随着集群规模的不断增加,显然无法满足集群回收的需求。
本文将基于视觉信息的无人机决策与模糊控制相结合,提出了一种基于模糊控制的集群自主着降算法,增加了集群系统的鲁棒性,提高了无人机集群安全回收的效率。
1 单无人机的自主着降
1.1 旋翼无人机视觉着降的主要步骤
旋翼无人机视觉自主着降首先通过GPS、惯性导航等导航设备到达降落航点,进行图像采集与降落标识检测,计算其与图像中心(u0,v0)的像素距离:
(1)
通过对像素坐标进行矩阵转换,求得无人机与降落点的实际水平距离,该距离误差较小,该信息再与气压计、陀螺仪传感器信息结合来解算视觉导引信号,最后向飞控发送导引指令控制旋翼无人机往靠近目标点的方向飞行,满足无人机与降落标识的实际水平距离小于指定阈值的条件后,进行着降[14]。
四旋翼无人机的视觉着降策略主要有2种方案[15]:①当检测到降落区域时,先控制旋翼无人机偏航角,使其航向与降落区域方向一致,再控制无人机俯仰角,使其做俯仰运动实现视觉导引;②保持旋翼无人机机头指向不变,直接计算旋翼无人机与降落区域的相对方向,控制无人机使其同时做俯仰与横滚运动以实现视觉导引。采用方案①,旋翼无人机需频繁地调整偏航角,且会对视野范围造成旋转,导引过程较为复杂,故采用方案②。
在旋翼无人机定点降落的过程中,本文采用阶梯式着降方式,即无人机与着降点距离小于等于预设阈值时,旋翼无人机进入降落模式,下降一定高度后,视觉测量精度提高,再进入导引模式,进行无人机与着降点水平误差修正,两种模式交替执行,最终实现着降。当旋翼无人机下降到一定高度时,会受到地面效应的影响,该影响会随着飞行高度的降低而增大,这对飞行的稳定性以及降落的精度都会造成一定的干扰。
1.2 坐标系构建与转换
通过视觉数据得到降落区域与无人机的像素位置后,需要经过多个坐标系之间的转换得到无人机相对于降落区域的实际位置[16-17]。
在摄像机成像模型中,需要考虑4个坐标系,分别是世界坐标系(OwXwYwZw)、摄像机坐标系(OcXcYcZc)、图像坐标系(O1xy)、像素坐标系(Ouv)。通过旋转平移、成像原理可以得到世界坐标系到像素坐标系的变换矩阵,再通过实验采集的真实数据与像素数据进行对比拟合,可得到变换矩阵的参数。
世界坐标系通过旋转平移变换可以转换到相机坐标系:
(2)
式中:R为旋转矩阵;T为平移矩阵。
由三维相机坐标系转换到二维图像坐标系,通过图1中小孔成像模型可得到变换矩阵:

图1 小孔成像模型
(3)
式中:f为相机中光学透镜的焦距。
图像坐标系是在物理成像平面中建立的二维坐标系,通过数字信号处理可以得到像素坐标系图像,见图2,变换矩阵见式(4)。

图2 物理成像坐标系与像素坐标系
(4)
式中:dx、dy分别为横向、纵向每个像素在物理成像平面上对应的实际距离;u0、v0为图像坐标系的原点在像素坐标系中的坐标值。
由式(2)~(4)可得世界坐标系到像素坐标系的变换矩阵,见式(5):
(5)
式中:
(6)
1.3 PID控制
PID控制器应用广泛,具有原理简单、易于实现的优点,其基本控制规律只有3个:比例控制、积分控制和微分控制,可单独也可组合使用。
PID控制离散化公式为:
u(t)=
(7)
式中:Kp(比例系数)用来控制当前,增大系统的比例系数可以加快系统的响应,减小静态误差,但是过大的比例系数会使系统产生超调甚至震荡,使系统稳定性变差。
Ki(积分系数)用来控制过去,对过去一段时间内的误差值进行求和求平均,找到预定值的平均误差。积分环节可以消除系统多余的纠正,有利于减小超调量,消除震荡,增加稳定性,但是会使系统静态误差消除时间变长。
Kd(微分系数)用来控制将来,通过计算误差的一阶导,控制系统对输出结果做出更快速的反应。有利于加快系统响应速度,但是系统对扰动的抑制能力减弱。
常规PID控制适用于简单的、参数固定不变的系统,对于复杂非线性的系统具有对突变敏感、抗干扰能力差等问题[18]。
2 无人机集群的自主着降
2.1 无人机集群降落标识设计
降落标识采用红色圆形,每个圆有一个数字,数字不重复。集群中无人机通过检测含有不同数字的红圆,找到自己的降落位置,如图3所示,其中r为无人机的安全距离,即以无人机为中心,半径为r的圆周范围内应避免其他物体的介入。在实际的集群着降中,r需要按照无人机结构与尺寸、机载硬件性能进行调整。

图3 集群降落标识设计
2.2 集群着降流程
本文集群着降采用分布式控制方法。每架无人机搭载简易的图像采集设备与处理系统,利用GPS或惯性导航等到达指定降落航点后,通过图像采集与处理,采用目标检测算法,找到本机的降落点(降落标识)。由于无人机自身机械振动和复合风场环境等因素的干扰,机载传感器存在测量误差,误差来源见式(8):
N∝Vte+εde
(8)
式中:V为无人机的速度;te为目标检测算法处理1帧图像的时间;ε为由变换矩阵求出的像素比;de为目标检测框中心与真实目标中心的像素偏差。在PID控制下测量误差会引起无人机的过调,这种过调给集群着降带来了极大的相撞风险。
模糊计算对于灵敏度和精确度要求较低,而且可以突出传感器数据中的主要信息,保证信息处理的实时性、多功能性和满意性[19]。因此无人机集群分布式着降中采用模糊算法进行降落,降低干扰影响与相撞风险。基于模糊控制的集群分布式着降流程见图4。若连续10帧没有捕捉到对应的降落标识,则升高2 m扩大视野继续检测,若当前高度超过指定高度,则向地面站发送指令,请求人工降落。

图4 集群分布式着降流程图
3 模糊控制算法
3.1 模糊化输入
在视觉引导着降策略中,误差e为降落区域的像素位置与图像中心处的欧式距离通过像素比得到的无人机与降落区中心的实际水平距离,见式(9)。
e=εdt
(9)
式中:dt是像素距离。
取输入变量为误差e和误差变化率ec,输出变量为速度v与加速度a。将输入输出变量分为5个模糊子集:正大(PM)、正小(PS)、零(ZO)、负小(NS)、负大(NM)。输入输出变量的论域均为[-10,10]。
3.2 构建隶属度函数
输入输出变量的隶属度函数如图5所示。

图5 模糊控制的隶属度函数
3.3 模糊规则构建
模糊控制规则是模糊控制的关键,本文根据专家经验设计模糊规则,模糊规则设计的标准为:“误差越小,速度越小”“误差越大,速度越大”;“误差变化率越小,加速度越小”“误差变化率越大,加速度越大”。具体模糊规则如表1。
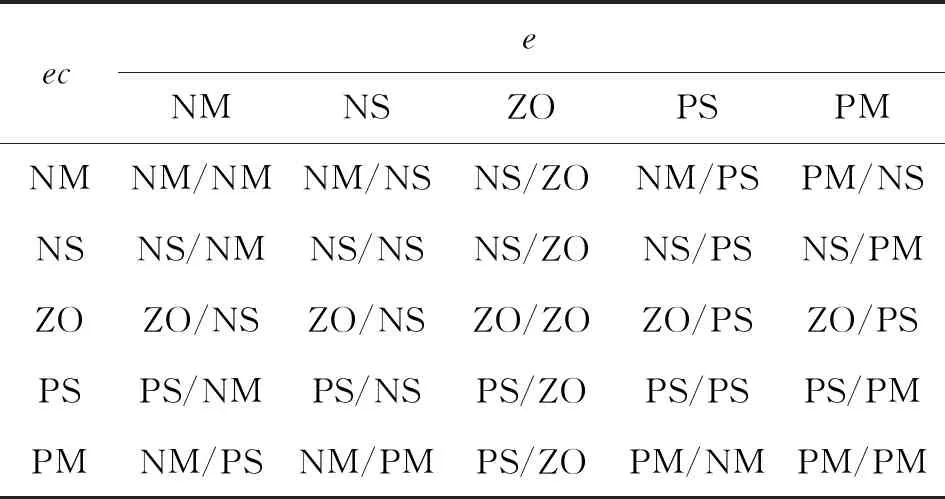
表1 模糊控制规则表
3.4 去模糊化
模糊控制输出的模糊量并不能直接用于控制执行机构,需要将模糊量去模糊化转换为一个精确量,本文采用重心法去模糊化[20]。
(10)
式中:μ(z)为输出量z所在模糊集合的隶属度函数,z0为模糊推理得到的精确量。z0的范围可能和执行机构要求的不一致,还需要进行论域变换:
(11)
式中:k=(umax-umin)/(zmax-zmin)为比例分子,[umin,umax]为实际控制量的变化范围,[zmin,zmax]为z0的变化范围。解算出v与a的精确量之后,采用加权和v=λv+(1-λ)a决定最终的速度控制量,使无人机飞行状态更加平滑。
4 实验与分析
4.1 模糊控制仿真实验与分析
为比较常规PID控制与本文提出的模糊控制在自主着降中的性能,使用MATLAB软件进行仿真验证。设置无人机的初始高度为30 m,目标在视野中的初始像素位置为u=350,v=250,通过对机载吊舱的标定,可以得到此时像素比ε1=0.024,由式(8)可得目标与视野中心的距离e=10.322 8 m。为防止降落高度后视野减小,丢失目标。当目标中心点与视野中心实际距离在0.2 m以内时,降落到当前高度的60%;当无人机高度小于8 m且目标中心点距离视野中心小于0.1 m时,则直接降落。
仿真中无人机的速度设置为0~10 m/s,de与te由网络模型和设备性能决定,对于目前的机载设备与目标检测模型,有te≤50 ms,de≤10 pixel,测量误差N与实际距离的比值N/e≤0.74。故在仿真的测量数据中叠加均值为0,标准差为0.1、0.3、0.5的随机白噪声以考证本文方法的有效性,仿真结果如图6。

图6 PID控制与模糊控制降落性能对比
可以看到,当σ=0.1时,PID控制与模糊控制性能差距较小,都能在6 s内成功降落;当σ=0.3时,PID控制在20 s内降落,模糊控制可以在10 s内降落,且模糊控制的速度曲线更为平滑;当σ=0.5时,PID控制在20 s内无法成功着降,模糊控制依然可以在10 s内成功降落。
进行1 000次Monte Carlo仿真实验,计算出PID控制与模糊控制的降落成功率和平均降落时间,如表2。降落成功率指降落成功次数在仿真总次数中的比例,平均降落时间指在降落成功的实验中降落时间的均值。

表2 PID控制与模糊控制降落成功率、平均降落时间对比
由表2可以看到,随着噪声方差的增大,PID控制的降落成功率快速降低,从100%下降到9.80%,模糊控制从98.20%下降到70.60%,显然,模糊控制鲁棒性优于PID控制。
值得注意的是,当σ=0.1时,PID控制的降落成功率为100%,而模糊控制为98.20%,这是由于模糊控制对于噪声的不敏感造成的,当误差较小时,模糊控制认为此时不需要改变控制量,而PID控制时刻对误差进行控制量调整。
4.2 无人机集群着降实验
实验平台为5架1 000 mm轴距四旋翼无人机,机载模块具体规格参数如表3所示。

表3 机载模块参数
实验的具体流程为:5架无人机在起飞区进行参数自检,并旋翼怠速旋转5 s,然后向地面站反馈自检结果。确认所有无人机状态正常后,发送起飞指令,所有无人机同时起飞,飞向指定降落航点。到达降落航点后,机载吊舱采集图像,并将图像传输给Jeston Xavier NX开发板,通过预训练好的YOLOv5算法检测无人机对应的降落标识,降落标识用含有数字1~5的红色圆形来表示,计算无人机与降落标识之间的水平距离,通过模糊控制处理得到控制指令,进行着降控制。为避免飞行过程中发生相撞,每架无人机飞行高度依次设置为6 m、8 m、10 m、12 m、14 m,利用高度差作为避撞措施。
本文使用模糊控制进行了2次5架机着降实现,每架机之间独立决策,等同于对模糊控制进行了10次实验。从图7无人机集群自主着降的整个过程拍摄实物图可以看出,无人机能够准确安全地降落在各自的降落点上。

图7 集群着降实验
本文对获得的实验数据进行了统计分析,得到不同初始高度下的平均降落时间与平均降落偏差,如表4所示。并对其中一组数据绘制了高度变化图和轨迹变化图,如图8和图9所示。发送起飞指令后,无人机依次响应,上升到指定高度,飞往对应的降落航点,检测对应的降落标识,经过调整后,高度小于9 m的无人机直接降落,高度大于9 m的无人机降落到当前高度的60%,继续进行检测与调整,达到降落要求后执行降落指令。在400 s内,所有高度无人机都可以成功降落。

表4 模糊控制平均降落时间、平均降落偏差

图8 集群着降实验高度变化图

图9 集群着降实验轨迹变化图
5 结语
本文针对无人机集群的自主着降问题,分析了单机着降与集群着降的区别,给出了集群着降分布式控制的方法。考虑到复合风场与传感器误差的影响,为防止过调造成的相撞风险,结合视觉导引信息,构建了一个模糊控制器,对传统PID控制与模糊控制进行了仿真对比,并进行5架无人机实飞实验。仿真实验与实际飞行实验表明,PID控制器对于噪声干扰的抑制效果很差,难以达到降落要求,模糊控制可以有效抑制干扰影响,防止无人机在着降过程中陷入死锁,提高集群着降速度与鲁棒性。
