不同影响因素下动态置换法压井参数研究

2021-09-22王志伟张伟国覃建宇王堂青

钻采工艺 2021年4期

王志伟, 陆峰, 张伟国, 金颢，覃建宇, 王堂青

1中海石油(中国)有限公司深圳分公司 2中国石油川庆钻探工程有限公司试修公司

0 引言

常规循环压井方法都是以U型管模型为基础，要求满足钻具与环空连通，钻头在井底，关井后不发生井漏等条件[1]。然而，对于异常高压、含硫化氢等特殊储层，井控风险大，井控难度高，且可能存在压井时钻具远离井底、钻具内通道堵塞，甚至井筒内无钻具的特殊情况，此时，常规压井方法收效甚微，需采用非常规压井方法[2]。非常规压井方法包括动力压井法、分步压井法、压回法、静态置换法和动态置换法[3- 6]。

分步压井法在实践时难以实现，动力压井法和静态置换法压井时间长、井口回压高、对井控设备要求高[4]。相比而言，动态置换法压井采用注液—排气同时进行的操作方法，大大减少了压井时间，降低了井口回压。任美鹏基于Wallis的液泛公式建立了动态置换法压井数学模型，但是该模型没有考虑井斜角、钻柱偏心和表面张力的影响。本文旨在建立新的动态置换法压井数学模型，讨论气柱体积、井斜角、钻杆偏心率、压井液黏度和表面张力对压井液最大注入排量和套压的影响规律，为动态置换法确定压井液最大注入排量提供理论基础。

1 动态置换法压井

动态置换法压井是一种准恒定井底压力的压井方法，压井液下落增加的静液柱压力等于排出井内气体降低的套管压力。与静态置换法相比，其不用等待压井液下落，可同时从压井管线注入压井液和从节流管线排出气体。动态置换法适用于钻柱堵塞、钻柱不在井底或井内无钻具等原因造成不能建立井口到井底循环的气井溢流或井喷[5]。

2 动态置换法压井数学模型

2.1 模型建立

2.1.1 压井液注入过程中井底压力恒定

为维持井底压力平衡，注入压井液与排出气体所产生的液柱压力之差等于套管环空压力的减小值，即：

ρkghk-g(ρg0hg0-ρghg)=pc0-pc

(1)

式中：ρk—压井液密度，kg/m3；

ρg0—初始时刻气体密度，kg/m3；

ρg—t时刻气体密度，kg/m3；

hk—井筒内压井液高度，m；

hg0—初始时刻井筒内气柱高度，m；

hg—t时刻井筒内气柱高度，m；

g—重力加速度，m/s2；

pc0—初始时刻套压，MPa；

pc—t时刻套压，MPa。

井筒内气柱气体的密度与压井液密度相比，可以忽略不计，因此式(1)可表示为：

ρkghk=pc0-pc

(2)

式(2)中，hk可由式(3)计算：

(3)

其中：

Qk=vskAe

(4)

同理：

Qg=vsgAe

(5)

式中：Qk—压井液排量，L/s；

Ae—等效环空横截面积，m2；

vsg—气体表观速度，m/s；

vsk—压井液表观速度，m/s。

2.1.2 气体排出过程满足物质守恒

根据物质守恒定律可知，t时刻注入压井液的体积等于排出气体的体积与因压力变化而减小的气体体积之和，即：

(6)

式中：Qk—压井液排量，L/s；

Qg—气体排量，L/s；

Cg—气体压缩系数，MPa-1；

Vg—井筒内气体体积，L。

2.1.3 压井液注入速度和气体排出速度满足液泛约束

式(1)和式(3)成立的前提条件是注入的压井液能够全部下落到井筒中，而压井液是否可以全部下落到井筒可根据液泛现象予以解释。

液泛指在流通通道内，气液两相逆流接触，当气体流速达到某一临界值，气体会把液体以液滴的形式携带至气体出口的气体携液现象。当气体的流速较小或为0时，液体会以光滑液膜的形式沿着管壁向下流动，随着气体流速的增加，液膜会呈波浪形并会伴有液滴随气流向上运动，随着气体流速继续增加，部分液膜的流动方向会发生改变，液体将会以液膜和液滴的形式随气体携带出去，随着气体流速的进一步增加，液膜的流动方向完全反转，所有液体都被气体带出去。如果在此时降低气体的泵入速度，则会出现部分大的液滴回落，液膜有向下流动的趋势，继续降低气体流速，会出现同时向上和向下运动的液膜，进一步降低气体流速，液膜和液滴将均向下运动[7- 10]。

选择合适的液泛关联式是动态置换法压井数学模型的关键，Wallis关联式没有考虑气柱体积、井斜角、钻柱偏心率、压井液黏度和表面张力的影响。本文以Drosos液泛关联式为基础，修正Drosos关联式，并定义环空等效直径，以讨论气柱体积、井斜角、钻柱偏心率、压井液黏度和表面张力对压井液最大注入排量的影响。式(7)～式(9)为修正后的Drosos液泛关联式[11]：

(7)

(8)

(9)

欲使压井液全部下落到井筒内，需满足式(10)：

(10)

式中：Frgs—气体Froude数；

Frks—液体Froude数；

Ka—Kapitza数；

cft—经验系数，0.0138；

De—环空等效直径，m；

θ—井斜角，°；

σ—表面张力，N/m；

μk—压井液黏度，Pa·s。

其中，环空等效直径由式(11)计算[12]：

(11)

(12)

(13)

式中：Do—井筒内径，m；

Di—钻柱外径，m；

P4(Z0)、P3(Z0)—4阶、3阶勒让德多项式；

ε—钻柱偏心率。

2.2 模型求解

联立式(1)～式(6)可得：

(14)

将式(14)与式(7)～式(10)联立可得压井液排量Qk关系式为：

(15)

将式(15)与式(2)联立可得t时刻套压随时间的关系式为：

(16)

2.3 模型验证

为了验证笔者模型的准确性，在井口温度为297 K，套管内径152 mm，气柱体积为6.3 m3，压井液密度为1.0 g/cm3，黏度为0.025 Pa·s，表面张力0.030 N/m，利用任美鹏模型[13]和笔者模型分别计算出在4.83 MPa和3.10 MPa井口压力下的气液表观速度比，与Ramtahal实验数据相对比，见表1。

表1 气液速度比

Ramtahal通过现场实验测定井口压力为0.103 MPa，井口温度为297 K，气柱体积为0.83 m3，压井液密度为1.0 g/cm3，黏度为0.025 Pa·s，表面张力为0.030 N/m，套管内径152 mm，分别在无钻具和钻杆外径51 mm下，测得最大注入排量分别为1.50 L/s和2.10 L/s。利用任美鹏模型和笔者模型在同等实验条件下，分别计算出最大注入排量，与Ramtahal实验数据相对比，如表2所示。

表2 最大注入排量

从表1和表2结果对比可以看出，本文所建立模型更接近Ramtahal实验数据，可以应用到动态置换法压井参数计算中。

3 影响因素分析

基于本文所建立的数学模型，单独分析气柱体积、井斜角、钻柱偏心率、压井液黏度和表面张力对压井液最大注入排量的影响规律，并分析井口套压随压井时间的变化规律。

3.1 气柱体积的影响

图1显示了井斜角为0，钻柱偏心率为0，压井液黏度为0.001 Pa·s，井口套压分别为3.0 MPa、4.5 MPa、6.0 MPa工况下，压井液最大注入排量随气柱体积的变化。可以看到：随着气柱体积增加，压井液最大注入排量减小。这是因为气柱体积增加，下落时间增加，要使压井液全部下落到井底，需减小注入速度。此外，随着井口套压增加，压井液最大注入排量降低，原因在于井口压力增加，导致气体密度增加，进而导致压井液受到气体的浮力增加，下落时间增加，因此，压井液最大注入排量减小。

图1 不同套压下气柱体积对压井液最大注入排量的影响

图2显示了初始套压为6.0 MPa，气柱体积分别为3 m3、9 m3、15 m3、27 m3条件下，井口套压随压井时间的变化趋势。可以看到：随着气柱体积增加，套压减小的越慢，套压降低至0 MPa时间越长，压井成功所需要的时间越长。这是因为如图1所示，气柱体积越大，压井液最大注入排量越小，导致压井时间增加。

图2 不同气柱体积下压井时间对套压的影响

3.2 井斜角的影响

图3显示了初始关井套压为6.0 MPa，气柱体积分别为3 m3、9 m3、15 m3、27 m3条件下，压井液最大注入排量随井斜角的变化规律。可以看到：随着井斜角增加，压井液最大注入排量减小，且减小的趋势越来越快。这是因为随着井斜角增大，压井液沿井轴方向所受重力减小，导致浮力与井轴方向重力差增加，进而导致压井液下落速度减小，因此，压井液最大注入排量减小。值得注意的是，气柱体积较大时，井斜角对压井液最大注入排量的影响不明显，这是因为当气柱体积较大时，压井液所受浮力主要取决于气柱体积，而压井液沿井轴方向所受重力的扰动对浮力与井轴方向重力差影响不大，压井液下落速度主要取决于浮力。

图4显示了初始关井套压为6.0 MPa，气柱体积为3 m3，井斜角分别为0°、30°、60°、90°工况下，井口套压随压井时间的变化趋势。可以看到：井斜角越大，套压减小速度越慢，当井斜角为0时，10 min内，套压降至2.8 MPa，降低幅度为3.2 MPa，井斜角为30°时，套压降至3.0 MPa，降低幅度为3.0 MPa，井斜角为90°时，套压降至5.7 MPa，降低幅度仅仅为0.3 MPa，几乎没有降低，这说明了井斜角越大，压井时间越长。原因在于如图3所示，当井斜角较大时，压井液最大注入排量急剧减小。

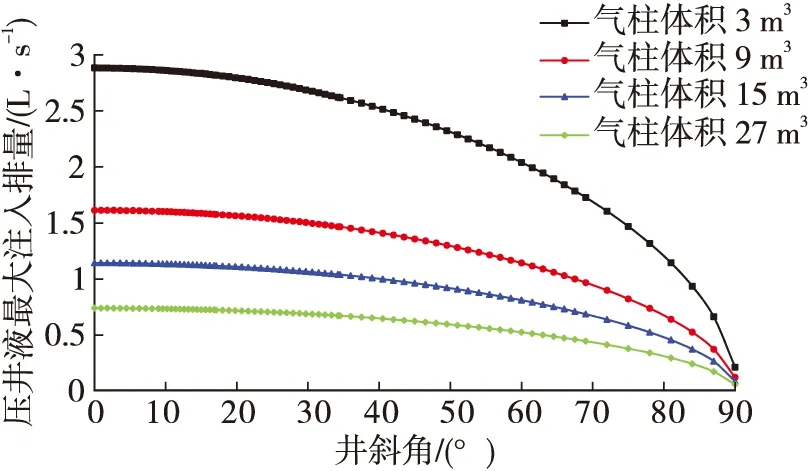
图3 不同立柱体积下井斜角对压井液最大注入排量的影响

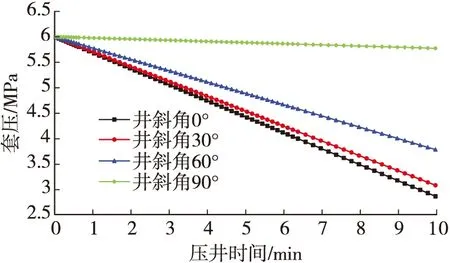
图4 不同井斜角压井时间对套压的影响

3.3 钻柱偏心率的影响

图5显示了初始关井套压6.0 MPa，气柱体积分别为3 m3、9 m3、15 m3、27 m3条件下，压井液最大注入排量随钻柱偏心率的变化趋势。可以看到：随着钻柱偏心率增加，压井液最大注入排量增加，且当钻柱偏心率超过0.4时，压井液最大注入排量急剧增加。这是因为，钻柱偏心率增加，导致井内等效环空直径增加，从而过流面积增加，当钻柱偏心率较小时，等效环空直径增加不明显，因此最大排量增加不明显，当偏心率超过0.4时，等效环空直径明显增加，最大排量也随之明显增加。

图5 不同气柱体积下钻柱偏心率对压井液最大注入排量的影响

图6显示了初始关井套压为6.0 MPa，气柱体积为3.0 m3，钻柱偏心率分别为0、0.25、0.5、0.75工况下，井口套压随压井时间的变化趋势。可以看到:随着钻柱偏心率增加，压井液最大注入排量越大，套压降低速度增加，所需压井时间越少。

图6 不同钻柱偏心率下压井时间对套压的影响

3.4 压井液黏度的影响

图7显示了在初始关井套压6.0 MPa，气柱体积分别为3 m3、9 m3、15 m3、27 m3条件下，压井液最大注入排量随压井液黏度的变化趋势。可以看到:当压井液黏度小于0.005 Pa·s时，压井液最大注入排量随黏度增加急剧减小，当黏度大于0.010 Pa·s时，排量随黏度增加减小，但减小不明显。这是因为，压井液黏度越大，压井液所受井壁、钻柱以及气体的摩擦力越大，导致下落速度减小，因此，压井液最大注入排量减小。当压井液黏度增加到一定程度时，继续增加黏度对摩擦力影响较小，导致压井液最大注入排量减小不明显。

图7 不同气柱体积下黏度对压井液最大注入排量的影响

图8显示了初始关井套压6.0 MPa，气柱体积为3.0 m3，压井液黏度分别为0.001 Pa·s、0.015 Pa·s、0.030 Pa·s、0.045 Pa·s工况下，井口套压随压井时间的变化趋势。可以看到:压井液黏度越大，套压降低速度越慢，当黏度为0.001 Pa·s时，10 min内便可压井成功；当黏度为0.015 Pa·s时，10 min后套压仅降至2.5 MPa左右。原因在于，黏度越大，压井液所受向上的摩擦力越大，减小了压井液下落速度，从而增加套压降至0的时间，延长了压井时间，当黏度大于0.030 Pa·s后，黏度增加对套压影响不大。

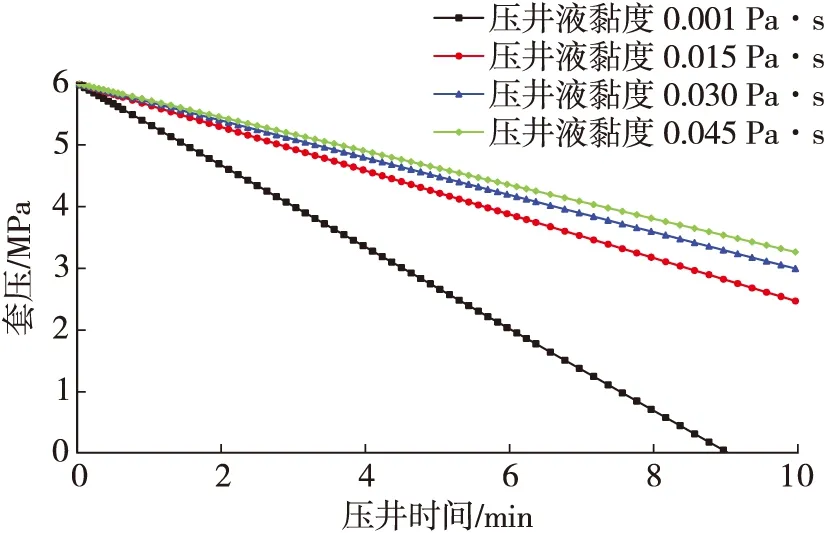
图8 不同压井液黏度下压井时间对套压的影响

3.5 表面张力的影响

图9显示了在初始关井套压6.0 MPa，气柱体积分别为3 m3、9 m3、15 m3、27 m3条件下，压井液最大注入排量随表面张力的变化趋势。可以看到:表面张力越大，压井液最大注入排量越大，表面张力小于0.010 N/m时，表面张力对压井液排量影响显著；当表面张力大于0.010 N/m后，影响不大。原因在于，表面张力越小，压井液越容易润湿井壁，造成压井液与井壁接触面积增大，压井液下落速度增大，进而导致压井液最大注入排量越大。