职业院校教学方案评价指标体系的构建
——以河北省职业院校技能大赛为例
2021-09-22谢珺
谢 珺
(河北师范大学,河北 石家庄 050024)
教学方案是对整个课程教学实施的计划安排。2020年9月份,由教育部等部门印发的《职业教育提质培优行动计划(2020-2023年)》指出职业教育教学评价体系要更具有职教特色。2020年10月,由中共中央、国务院印发的《深化新时代教育评价改革总体方案》提出要提高教育评价的科学性、专业性、客观性,但如何对职业院校教学方案进行科学、有效的评价,目前的相关文件政策并未说明。在中国知网以“教学方案评价”为关键词进行搜索,查阅相关文献500篇,涉及到“评价体系”的文献只有133篇,评价对象更多地集中在课堂教学质量,对教学方案评价的研究几乎寥寥。同时,教学方案也是全国职业院校教师教学能力大赛的一项主要评价内容,但目前更多地是依靠于评委经验进行评分,缺乏一个合理、科学的教学方案评价指标体系。因此,建立一个职业院校教学方案的评价指标体系是当前亟需解决的问题。从实证研究角度,本文采用因子分析法、AHP层次分析法、信度和效度分析拟构建一个合理、科学的职业院校教学教案评价指标体系。
一、确定评价指标
因子分析法最初是由英国心理学家C.E.斯皮尔曼提出,这种方法是将多个实测变量转化为几个无相关性综合指标的统计分析方法[1]。这种方法可在若干变量中找出具有代表性、潜在性和共同性的因子,再进行归类,将具有相同本质的变量归为一个因子里。运用这种方法,一方面能够减少变量的数目,另一方面也可检验变量之间关系的假设[2]。为了使职业院校教学方案的评价指标体系更具有科学性,将采用因子分析法确定评价指标。首先,考察原有的变量是否满足因子分析的条件。其次,将从若干个变量中提取公共因子,并确定公共因子的数量。最后,对公共因子进行命名。
(一)样本选取
依据职业教育教学的特点,并结合2020年全国职业院校技能大赛中的评价标准,并通过专家讨论,最终确定影响教学方案评价的十三个指标。确定的指标分别是“教学环节设计”“教学方法”“课后反馈”“教学策略”“教学目标”“学情分析”“信息技术应用”“教学模式”“外观保存”“结构完整”“教学内容”“教学重难点”“课后总结”。河北省职业院校技能大赛的评分专家根据确定的指标分别对河北省职业院校技能大赛的42份教案进行评分,因子分析的数据是根据以上的十三个指标所打出的42份教学方案的分数。
(二)因子分析的前提条件
在进行因子分析前,要考察运用此方法提取公共因子是否合适,进行适用性检测[3]。经检验,KMO值为0.885,大于0.6,较为适合做因子分析。其中,Bartlett 的球形度P值为0.000,P=0.000<0.05,解释为所有变量适合做因子分析,适用性检测通过。
(三)提取主成分确定公因子
表1给出了公共因子总方差的解释,即每一个公共因子对全部原始变量总方差的贡献率。从表格得知,提取的三个公因子解释了原始变量总方差的86.539%,其数值超过80%,表明提取的三个公因子在很大程度上描述了原始变量的信息。

表1 总方差的解释
(四)因子旋转和命名
通过因子旋转矩阵,我们取得了三个公因子,下表表示的是它所包含的变量。将公共因子一命名为“教案内容”;将因子二命名为“特色创新”;将因子三命名为“教案形式”,如表2所示。

表2 职业院校教学方案评价指标
二、模型建立
层次分析法是由美国运筹学家托马斯·塞蒂教授提出的,通过分析复杂的问题所包含的要素和其关联性,对多准则的决策问题作出科学且综合的评价[4]。本研究以河北省职业院校技能大赛的教案为研究对象,运用因子分析法提取主要指标,并结合层次分析法和综合专家意见,构建一个适用于职业教育使用的评价指标体系。本次模型建立共分为三个部分:
(一)构建判断矩阵
在一定的准则下,每一层的元素与同层元素相比,权重是不同的。因此,同一层的各元素的重要性需要进行两两比较来构建判断矩阵[5]。为了量化评价判断,在判断矩阵的构建过程中,采用表3所示的1-9比例标度法。根据1-9比例标度法,对同层的各因素进行两两比较评分。一共请八位专家进行评分,以下步骤将选取其中一位专家评分数据为例进行说明。例如:在一级指标判断矩阵中,教学内容Q2比特色创新Q3明显重要,其数值为“1/5”,其倒数则为:“5”。依照此方法,分别构造一级指标判断矩阵和二级指标判断矩阵,如表4、表5、表6、表7所示。

表3 1-9比例标度

表4 一级指标判断矩阵

表5 二级指标判断矩阵(一)

表6 二级指标判断矩阵(二)

表7 二级指标判断矩阵(三)
(二)层次单排序及一致性检验
层次单排序就是要计算判断矩阵的最大特征向量,把本层的各元素对上一层而言,各元素做出评比顺序。由于判断矩阵具有误差,在给各指标进行优先排序时可运用和积近似算法,不需要较高的精确度。相对重要度计算时,可先计算判断矩阵的最大特征根,其次计算其对应的特征向量[6]。以一级指标为例,其计算步骤如下:
首先,将判断矩阵各列正规化,公式如下:
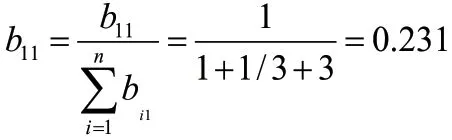
用同样的方法计算可得出正规化后的判断矩阵:

λmax=3.006计算具体过程如下:

然后再计算一致性指标CI,通常情况下,CI≤0,该判断矩阵具有一致性。其中如出现判断矩阵完全一致时,CI则等于0。

表8给出了随机一致性检验指标,首行是阶数,根据阶数找到相对应的RI值。

表8 1-9阶矩阵的平均随机一致性指标
随机一致性比例,记为CR,是CI与RI的比值。
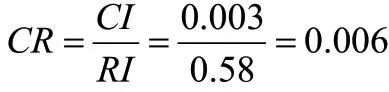
CR≤0.10,即通过一致性检验。CR≥0.10,即未通过一致性检验,则需要调整。
经过计算,得出一级指标权重及一致性检验,如表9所示:

表9 一级指标权重及一致性检验
(三)分析计算结果
对二级指标及其他七位专家的判断矩阵进行一次性检验,检验均通过。计算出相应的权重,将八位专家的权重向量进行加权平均,得出最终的指标体系。其中一级指标为教案形式,教学内容,特色创新,平均值分别为0.31,0.45,0.24。
一级指标教案形式下的二级指标外观保存,结构完整,平均值分别为0.52,0.48。一级指标教案内容下的二级指标教学目标,学情分析,教学内容,教学策略,教学环节设计,教学方法,教学重难点,课后反馈,课后总结的平均值分别为0.04,0.04,0.09,0.11,0.32,0.17,0.04,0.09,0.09。一级指标特色创新下的二级指标信息技术应用和教学模式的平均值分别为0.75,0.25。
(四)指标体系的应用
对八位专家的权重进行加权平均,得出权重,根据其权重,对每一项指标进行分值分配,建立评分表。评分表中的指标体系中分别设五级评分等级A、B、C、D、E,分别为1分、0.8分、0.6分、0.4分、0.2分。评分结果大于等于90分,设为优秀;80至89分,设为良好;60至79分,设为合格;小于60分,设为不合格。经过量化的教案评分表如表10所示。
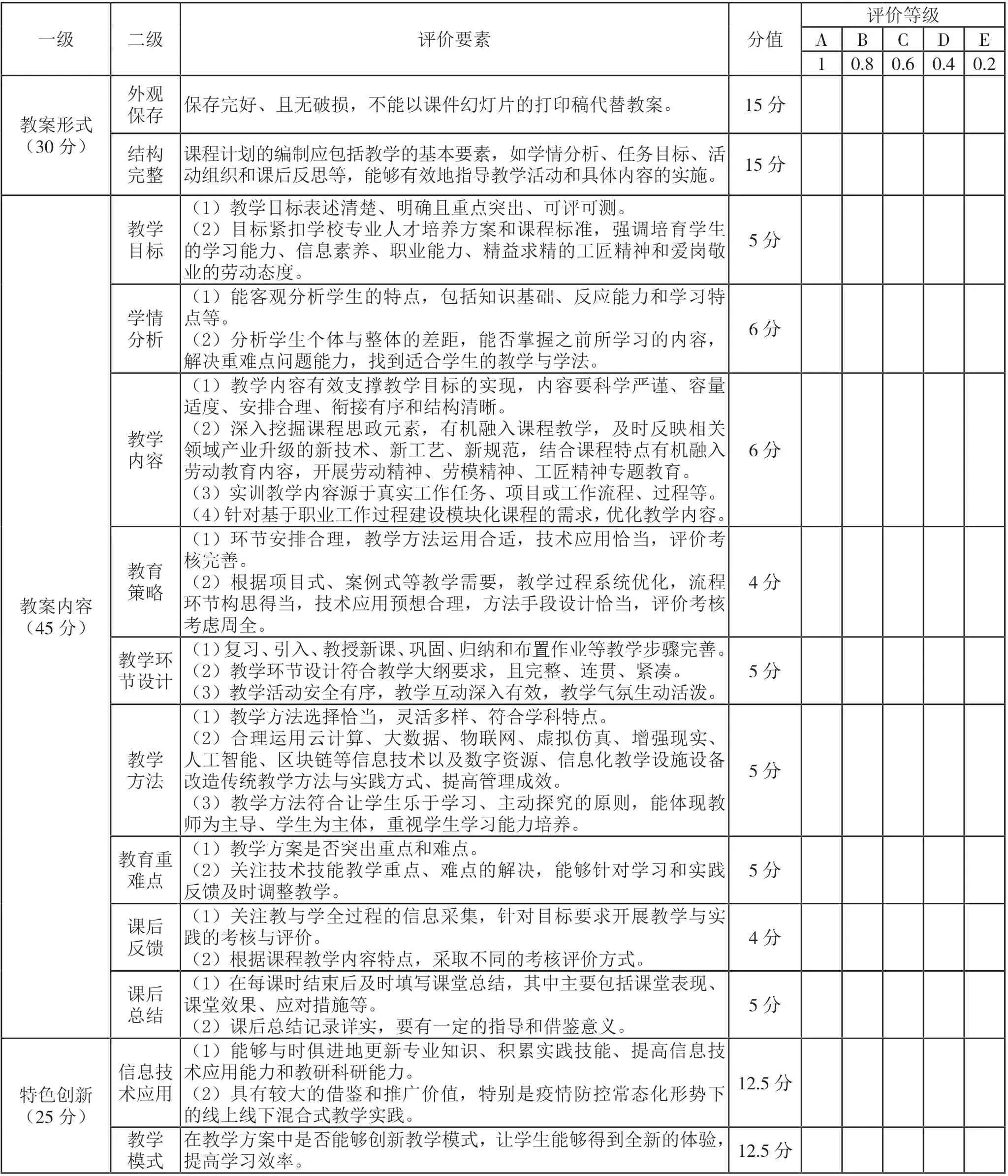
表10 教案评分表
三、信度与效度分析
为了检验该教案评分表是否具有可靠性、有效性和准确性,通过克朗巴赫α系数进行信度分析,通过效标关联效度分析法进行效度分析。
(一)信度分析
信度,广义上是指评价体系的可靠程度;狭义上则是指重复测量结果之间一致性的程度[7]。本文的信度分析则是对所构建的职业院校教学方案的评分表进行分析,测量其是否具有一定的稳定性和可靠性。
为了解本次所构建的职业院校教学方案评分表是否具有一定的可靠性和稳定性,以河北省职业院校技能大赛的教案评分数据为实例,根据评分数据对其信度进行分析,本次信度分析将采用克朗巴赫α系数进行分析。由信度分析结果可知,本次评分的指标有十三个,克朗巴赫α系数为0.939,此结果大于0.8,说明可靠性与稳定性高,其信度很好。
(二)效度分析
效度是指评价结果是否准确、有效,即测量是否达到了预期目标[8]。本文中的效度分析主要是对所构建的职业院校教学方案的评分表进行的测量和评价分析,了解评分表的准确性和有效性。
本研究将使用效标关联效度分析法,利用积差相关法分析评分表的效度。以河北省职业院校技能大赛的教案评分数据为实例,对比河北省职业院校技能大赛中的最终总得分,了解教案的得分情况是否影响总得分情况。得到教案得分与总得分的相关系数为0.960,说明本次考试与平时成绩的相关性较强,即本次评分表反映了河北省职业院校技能大赛的真实水平,有效性和准确性很好,符合效度要求。
四、结语
合理、科学的职业院校教学教案评价指标体系是审视职业院校教学效果的重要评价工具。本文以职业院校发展的特点,通过定量与定性分析,构建了涵盖一级指标三项,二级指标十三项的职业院校教学方案的评价指标体系。评价指标体系的应用有助于解决评价时主观性较强,不规范等问题,完善应用型人才培养体系。
