不同船速比对改向避让效果的影响
2021-09-18王兴华陈国权李丽娜李国定
王兴华,陈国权,李丽娜,李国定
(1.集美大学航海学院,福建 厦门 361021;2.集美大学船舶辅助导航工程国家地方联合研究中心,福建 厦门 361021)
0 引言
《国际海上避碰规则》(以下简称《规则》)首次被提案时,船舶之间的速度相差无几,且受当时通信条件限制,目标船速的获取较为困难,《规则》定义的避碰行为仅基于临近船舶的相对方位[1]。随着通信技术和船舶的多样化、大型化和高速化发展,目标船速度的获取较为容易,船速相差较大(K≥1.5)的情况也较为常见,船舶驾驶员在根据会遇态势制定避碰方案时,船速比已成为一个必须要考虑的重要因素。文献[1]在相对方位和速度比的基础上,用公式和曲线推导出避碰决策最有效的路径变化,但未建立船速比与改向幅度、施舵点的具体关系模型和避让优化方案;文献[2]提出基于多种群遗传算法自动生成最优避碰路径的船舶避碰辅助决策方法;文献[3-6]提出基于深度强化学习的船舶避碰方法;文献[7-8]提出根据目标船相对方位和船舶类型确定转向避碰的行动向量;文献[9]建立了基于涡旋势场的改向模型,根据旋涡势的矢量场引导船舶改向避开障碍物。文献[2-9]方法属于人工智能技术和方法,不考虑避碰问题中的抽象因素和避碰参数的量化问题,虽然理论可行,但实用性不足。文献[10-15]将避碰领域知识形式化,将定性的专家避碰经验知识与定量的数学模型进行有效融合,采用船舶相对运动几何建模,建立一系列的数学模型,构建动态避碰知识库,在自建推理机制的引导下,求取避碰决策方案。在船舶拟人智能避碰决策(personifying intelligent decision-making for vessel collision avoidance,PIDVCA)算法研究的过程中,发现基于《规则》进行改向避让的效果受船速比影响较大,会产生不合理的避让局面。因此,本文对船速比与施舵点、改向幅度关系进行建模,分析船速比(K≥1)分别对施舵点、改向幅度的影响,为自动避碰辅助决策研究提供参考。
1 船速比与改向幅度、施舵点的关系模型
1.1 目标交会特征分类
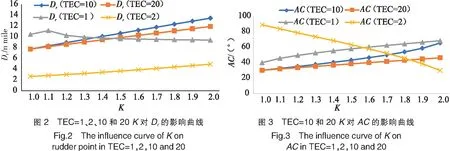
目标交会特征(target encounter characteristic,TEC)是指在根据目标船相对方位不同所形成的同一种会遇局面中,当本船速度Vo和目标船速度Vt的关系不同,以及目标船真航向Ct取值不同时,本船与目标船会存在不同的交会特征[1011]。通过计算两船的速度差Vt-Vo和航向差Ct-Co,并根据船舶相对运动航向Cr的取值范围来确定船舶会遇所属不同交会特征,如表1所示。例如,右舷前方区域交叉会遇,当目标船的相对运动航向Cr取值为180° 表1 目标交会特征取值表 表1中,当TEC=1,2,7,8,10,20,70,80时本船速度小于目标船,即Vo≤Vt。其中:TEC=1,2,10,20为前方交叉会遇局面;TEC=7,8,70,80为被追越或大角度交叉会遇局面。虽然不同目标交会特征下船速比与本船改向幅度、施舵点的关系模型不尽相同,但建模方法基本相同,故仅以TEC=10为例说明。限于篇幅,根据实际船舶航行会遇场景多为前方交叉局面且较为复杂,在分析船速比对改向避让效果影响时,仅以前方交叉会遇为例,取TEC=1,2,10,20进行分析。 (1) 其中:Cr与Crn分别代表本船改向前后目标船相对于本船的航向;sign(Dsa)为Dsa的符号函数,此例情况下sign(Dsa)=-1。 若本船单纯改向避让,新的相对运动速度Vrn和航向Crn的计算公式为: (2) Crn=180°+AC-arcsin[Vtsin(Ct-C0-AC)/Vrn]。 (3) 此时可得转向点N, (4) (5) 同时,对应的改向幅度AC=Crn-asin(sin(Ct-Crn-Co)×Vt/Vo)-180。其中:Crn=Cr+asin(Dsa/Dr)+asin(Dcpa/Dr) 同理,可得其他不同交会特征下船速比分别与改向幅度、施舵点的关系模型。 根据《规则》,在交叉相遇局面中,互见或能见度不良时,有他船位于本船右舷,本船应给他船让路,本船为让路船;互见中,他船位于本船的左舷,他船应给本船让路;能见度不良时,他船位于本船的左舷,本船亦有让路义务。因此,当TEC=2或20时,本船的避让时机为形成一般危险时,应避免进入紧迫局面。当TEC=1或10且互见时,本船为直航船,本船的避让时机为本船逼近到单凭让路船(目标船)的行动不能避免碰撞时,称为最晚施舵时机;当TEC=1或10且能见度不良时,避让时机与TEC=2和20一致。为便于对比说明,选取TEC=1、10且能见度不良和TEC=2、20互见本船避让时机一致的情况。 假定两船的船长、操纵性参数不变,目标船相对于本船的方位不变,两船安全会遇距离Dsa相同,设定为2 n mile,会遇距离不变,设定为14 n mile(nm),最近会遇距离Dcpa为0 n mile,本船速度设置为15 kn。交汇特征为TEC=1,2,10和20时,若本船向右等幅度改向30°,K值取1.0,1.1,1.2,…,2.0时,分析本船到施舵点的距离Dr的变化。当TEC=10和20时,本船向右改向30°,K对Dr的影响如下表2所示。 表2 TEC=10和20不同船速比与Dr的关系 若本船等距离改向,即Dr不变,其值取K=1.0时AC=30°的Dr,当K分别取值1.0,1.1,1.2,…,2.0时,分析AC的变化趋势。例如,当TEC=10和20时,Dr=7.727 n mile,K对AC的影响的变化如下表3所示。 表3 TEC=10和20不同船速比与AC的关系 为更直观,现将交叉局面TEC=1,2,10和20情况下,船速比K分别对本船到施舵点的距离Dr和改向幅度AC的影响用折线图展示,如图2和图3所示。 从图2和图3可以看出,在TEC=10且能见度不良时,本船按《规则》向右改向,若改向幅度不变,船速比K=2的施舵点几乎是K=1的二倍,即K=2的施舵时机要比K=1提早一倍;若本船的施舵点不变,K=2的改向幅度是K=1时的2倍。同理,TEC= 20且互见时,本船为让路船,当等幅度改向时,K值越大,施舵时机来的越早;当等距离改向时,K值越大,改向幅度越大。较为特殊的是TEC=1和TEC=2,当TEC=1且能见度不良时,若本船等幅度改向,随着K值的增大,施舵点呈现先升后降的趋势,这与本船过目标船艏或船尾有关,根据船舶相对运动几何变化规律亦可得出;当TEC=2且互见时,若本船等距离改向,随着K值的增大,改向幅度呈下降趋势。 为验证上述分析结论,在船舶智能操控仿真测试平台上对PIDVCA算法进行了大量仿真模拟实验。仿真实验表明,船速比较大的情况下(K≥1.5)若严格按照《规则》条款执行会出现不理想的避让效果,如图4所示。 TEC=20的交汇特征,目标船1设为本船,在互见情况下,按照《规则》的避让责任划分,本船为让路船,目标船2为直航船,本船按《规则》向右改向避让,因目标船速度远大于本船,本船的避让时机远远提前。由图4的仿真结果可以看出,本船的避让效果并不显著,即避让时机远远提前,其提前量取决于K值,其值越大,提前量越多。 现以能见度不良条件下左正横附近(247.5°<目标船相对方位<292.5°)来船且TEC=1为例,说明较高船速比对基于《规则》改向避让效果出现的不合理现象,并提出优化建议。如图5a)所示,在能见度不良情况下,目标船1和目标船2均应承担避让义务,目标船1因速度较小,避让时机较早,为了避开危险选择率先避让,目标船2在其避让时机到来时,因其碰撞危险消失而选择不采取避让行动,以致两船因相对运动速度很小而长时间僵持。显然,此种避让行为不利于船舶安全航行,不符合船舶避让的安全性、科学性和经济性。 为了解决上述问题,以航迹偏移量最小为目标,集成PIDVCA算法对避碰决策进行动态优化处理,优化结果如图5b)和图5c)所示。图5b)中,在能见度不良情况下,目标船1(互见低速直航船)的避让时机应选取互见情况下作为直航船的最晚施舵时机。图5c)中,在能见度不良情况下,避让方案的优化方法采取目标船2(互见高速让路船)主动提前履行避让义务,这时目标船1会因两船危险消失而保持直航。 由图5的模拟仿真例子可知,在能见度不良条件下,目标船1若按《规则》选择避让时机会形成不合理的避让效果,若按互见情况下选择避让时机,避让效果更优;或者,若“目标船2作为高速船能够承担更多的避让责任势必会使避让局势更和谐。 船舶智能避碰技术在应用过程中必须遵循《规则》要求,然而随着人工智能技术和计算机技术的迅猛发展推动着船舶向大型化、高速化、智能化方向发展,使得《规则》中的一些定义开始变得不够合理。《规则》定义的避碰行为通常只基于临近船舶的相对方位,在船速比相差无几且确定船速比较为困难的年代是完全合理的,但在高速船普遍存在和获取目标船船速较为容易的情况下,船速比对机器模拟船舶驾驶员制定改向避让方案的影响不可忽视。现将影响归纳如下: 1)互见情况下,在目标船与本船形成较高船速比的交叉会遇局面下,若本船按《规则》改向避让会出现避让效果不显著,即让路船的避碰行动远远提前,其提前量取决于K值,其值越大,提前量越多; 2)能见度不良情况下,在左正横附近(247.5°<目标船相对方位<292.5°)来船的交叉会遇局面下,按照《规则》改向避让在来船没有采取相应避让行动情况下可能产生安全隐患。 针对这些影响,建议在研究智能避碰决策时应“体现实践中对《规则》的合理延伸”来解决因严格按《规则》的避让行为所带来的避让效果不合理的现象。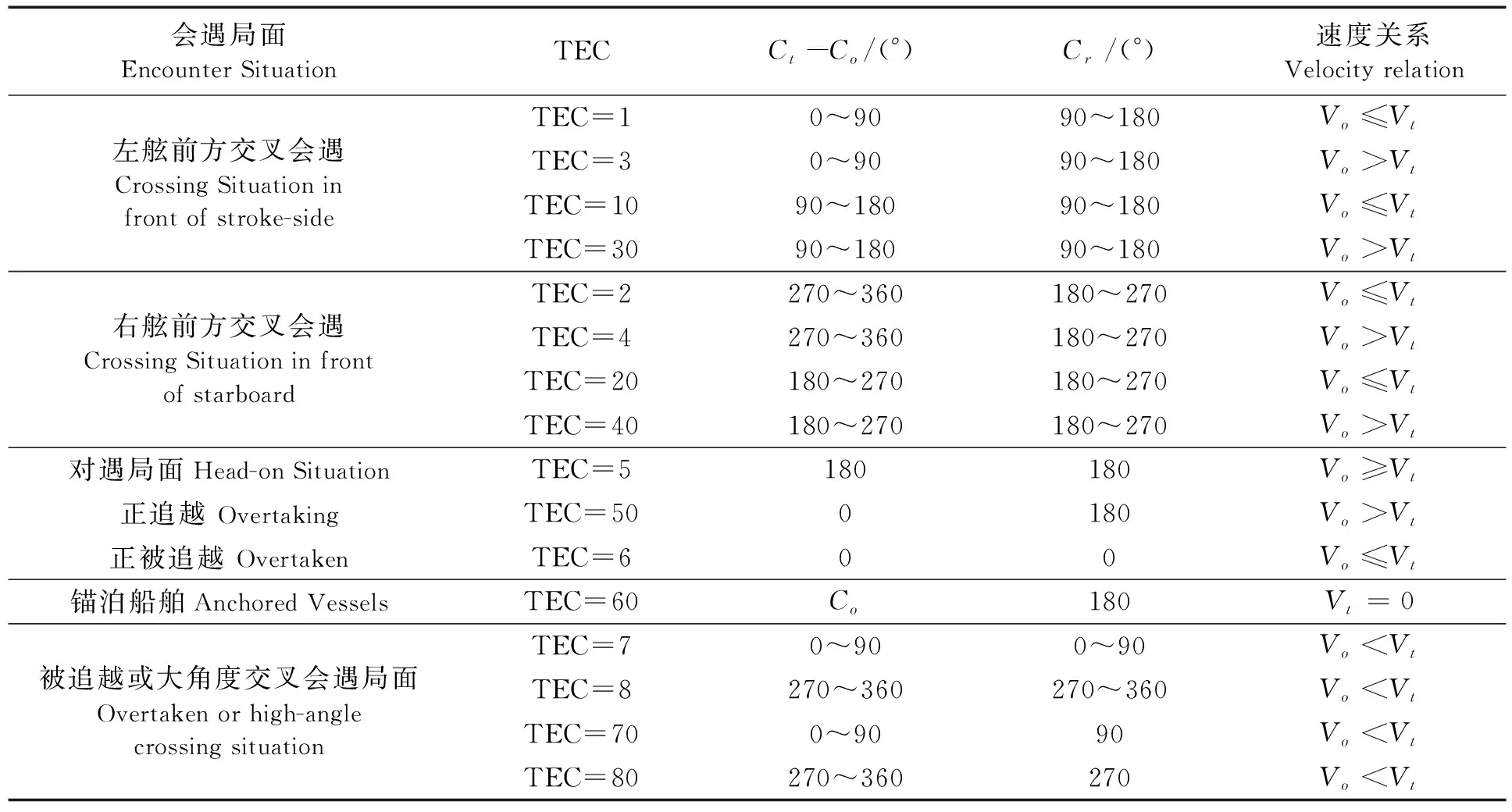
1.2 船速比与本船改向幅度、施舵点的关系模型

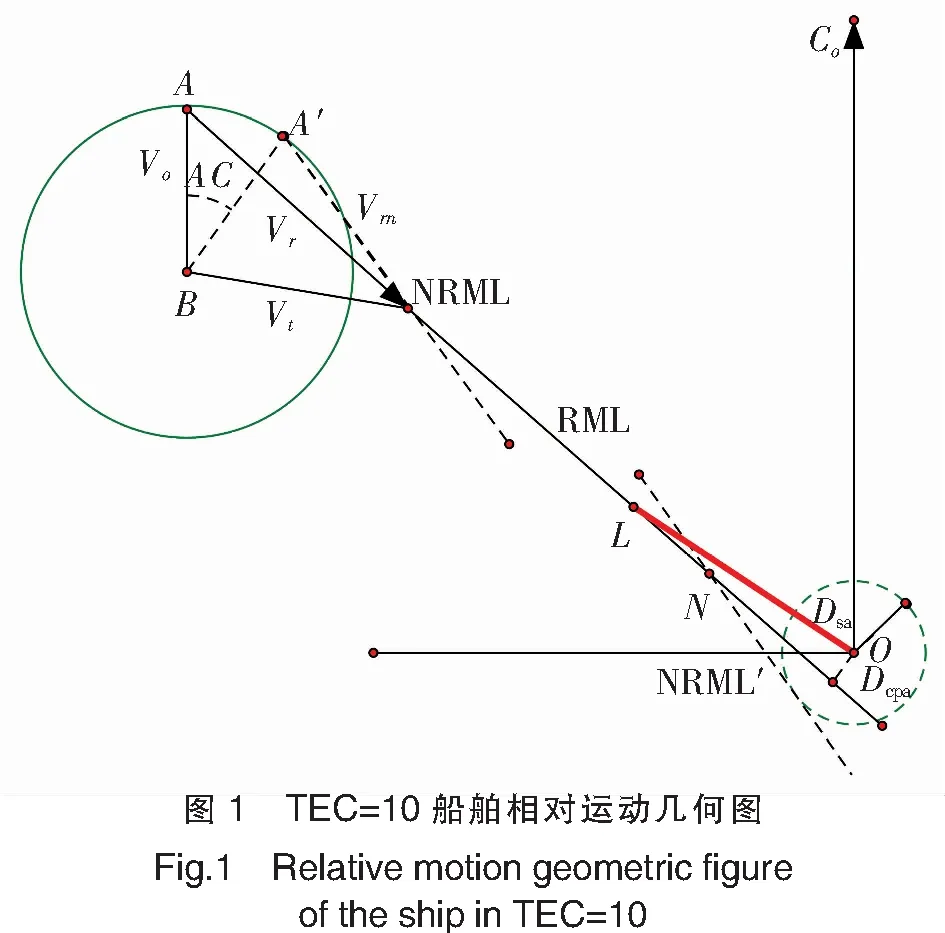


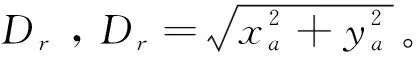
2 改向避让效果分析
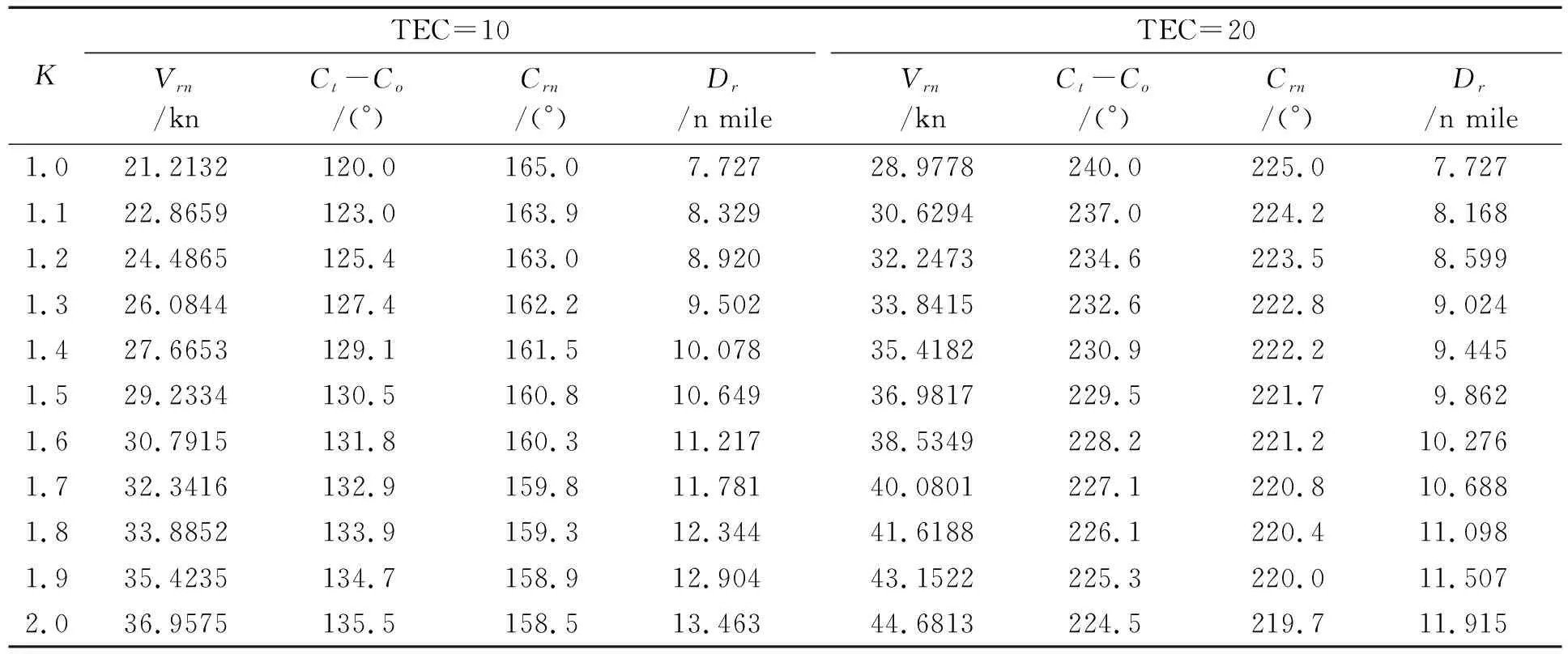

3 模拟仿真实验效果及避让决策优化


4 结论与建议
