连续性政策的效果评价方法研究

王 培

（浙大宁波理工学院，浙江 宁波 315100）

0 引言

改革开放以来，我国政府出台了大量的政策措施，对这些政策的实施效果进行科学地评价，其结果对深化改革的今天，有着重要的借鉴作用。但是，科学的政策评价对评价方法提出了较高的要求。

在政策评价的实际工作中，我们经常会面对针对某一目标的一系列政策，而单次政策出台的时间间隔通常不是固定的，政策的内容和力度也有所不同。如果我们仅关注这一系列连续性政策的整体最终效果，那么可以把它看成是一个整合在一起的单次政策效果评价，到目前为止，评价方法较为成熟，但是如果我们同时还关注各个单次政策出台后的中间效果，以便我们准确把握每个政策的具体方向与力度，那么之后的政策是对经济发展结果的适应性调整，也就是对之前的试点改革实施效果的适应。对连续性政策效果进行有效的评价，具有很强的现实意义。

1 政策评价模型介绍

1.1 DID 模型

倍差模型（difference in difference，简称DID）是政策评价的常用方法，基于微观数据，已有不少研究采用此模型对我国各种政策进行效果评价。郑新业等（2011）基于河南省数据估计了“省直管县”政策对经济增长的影响；针对多期（超过2 期）面板数据，戴嵘和曹建华（2015）采用DID 回归方程对我国首次“低碳试点”政策的减碳效果进行了估计。

DID 模型的思路是将样本分为干预组（受政策影响）和控制组（不受政策影响），假设在政策实施前后时期，被观察的个体保持不变，即样本数据为平衡面板数据，同时干预组和控制组中包含的个体不会发生互换。设哑变量：

ti表示个体i 所在时间：ti=0 政策实施前，ti=1 政策实施后。ri表示个体i 所在样本组：ri=0 没受到政策影响，ri=1 受到政策影响。

di=ri·ti，仅当干预组中的个体i 在时期2 时，有di=1。

根据潜在结果框架，每个个体无论在哪个时期，都可以同时出现两种情况：受到政策影响和不受政策影响。进而得到两种不同的结果，只是我们只能观察到其中的一种结果，另一种结果无法观察。针对每一个个体，我们有观察向量(Yt，r，t)，总体上的构成关系是：

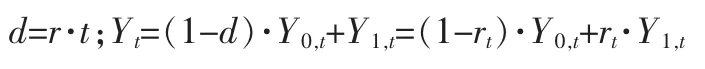
我们可以得到：

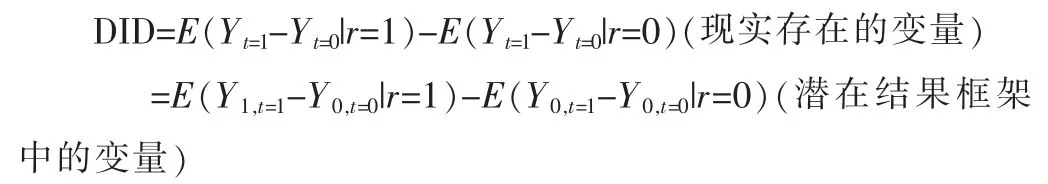
为了把DID 取值和政策效果联系起来，需要共同趋势假设：

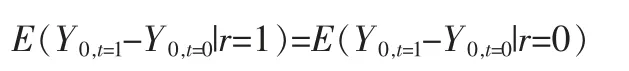
此假设要求如果没有政策的实施，干预组和控制组中个体变量变动的期望相同。若共同趋势假设成立，有：

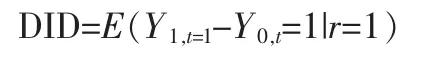
所以，DID 值即为干预组政策后的平均处理效应（ATT）。我们可以构造一个特有的线性回归方程，使DID 就是其中的一个交叉项前的系数，从而可以给出其渐进方差，进行显著性检验。线性回归方程是：

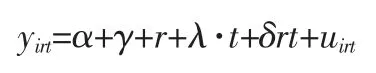
方程中的系数δ 即为我们感兴趣的DID 估计值。为了增强共同趋势假设成立的合理性，通常会利用加入控制变量Xrt对样本进行分层处理：

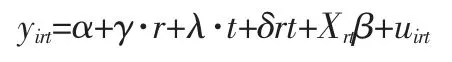
由于倍差模型思路清晰、方法简便，但其缺陷有：

（1）个体的内生性政策选择导致共同趋势假设不成立；

（2）倍差模型无法对连续性政策进行评价。

1.2 内生选择模型

上节说明，限制倍差模型应用的一个主要障碍是个体的内生性政策选择，这将导致共同趋势假设不成立，进而倍差模型不能适用。内生性政策选择是指个体可以根据自身状况选择性地接受政策的影响。比如小微企业通常会根据自身状况，选择性地接受一些财政金融扶持政策。

要解决这个问题，可以采用内生选择模型对政策进行评价。内生选择模型不仅考虑了每个样本个体对政策的选择性接受，同时还考虑了不同样本个体对政策的不同反应程度。内生选择模型可以构造如下参数模型：

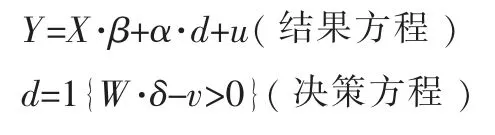
这里，X∈Rp，W∈Rq是由解释变量组成的向量，这两个向量中可以有重叠的元素，通常扰动项u 和v 是相关的，这使得u 和d 相关，产生内生性问题，我们不能单独对结果方程中代表政策效果的参数α 进行线性回归估计。

对此含有内生哑变元的政策评价模型，我们可以采用2 种方法进行估计：极大似然法和二步法。该模型不足之处为：

第一，要求服从正态分布，有较强的参数前提假定，而这对于微观样本来说，一般是难以满足的。

第二，政策效果参数α 针对不同的个体，是一个不变的常数。不允许个体对决策（政策）所做出随机的不同反应。

为了确保评价模型的稳健性，内生选择模型可采用半参数形式来构造。模型的构造如下：

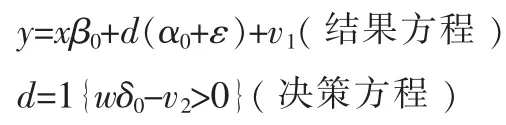
这里x，w 是由解释变量组成的向量，这两个向量中可以有重叠的元素。决策方程中展示的是政策选择的内部机制，包含一个潜在效用函数U=wδ0-v2，假设潜在的效应函数是线性形式；在结果方程中，d 是内生的哑变元，表示个体是否受到政策的影响，它带有一个随机系数α0＋ε。我们感兴趣的是政策效果参数α0，随机扰动项ε 反映了不同个体受到政策影响时的不同效果程度。

总之，如果我们能够得到一些影响政策选择的个体状况取值的话，利用上述参数或半参数内生选择模型，基本上能够解决政策评价中的内生性政策选择问题，但是仍旧无法处理连续性政策的评价问题。

1.3 回归合成法

在政策评价的实际操作中，我们经常会遇到干预组样本单一的问题，比如在对区域政策进行效果评价时，干预组通常只有唯一一个样本地区，而控制组的潜在样本有很多，但是并不确定。Hsiao 等（2012）提出的回归合成法解决了干预组样本单一问题。前面提到的谭娜和周先波（2015）与叶修群（2018）均采用此方法对区域政策的宏观经济指标效果进行了评价。

回归合成法采用回归的方法识别出处理前的干预组样本和其他控制组样本的相关性。然后利用这种相关性去预测干预组样本政策时点之后的潜在结果。注意这里并不需要共同趋势假设的成立。

具体我们设定N＋1 个观测个体，有T 期观测值。其中仅i＝1 为干预组样本，其他均为控制组样本，设政策干预时点为T0。设政策哑变量为：

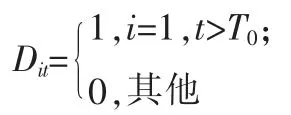
用（Y1ist，Y0ist）表示两个潜在结果，则有：

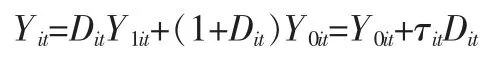
其中个体i 的第t 期政策效应为：τit=Y1it-Y0it

对于样本t≤T0，我们采用下列回归方程估计处理前的干预组样本和其他控制组样本的相关性：

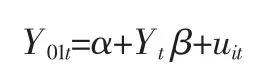
这里，Yt＝（Y2t，Y3t，…，YN＋1，t）。然后利用此方程的估计值，对政策时点之后的反现实结果进行预测：

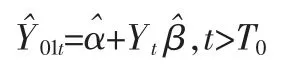
最后可得政策时点之后的干预个体政策效应估计：τ1t=

这里的控制组样本选择可以按照AIC 和AICC 标准进行选择，详见Hsiao 等（2012）的研究。回归合成法虽然方便地解决了干预组样本单一问题，同时也降低了控制组样本选择的主观性干扰，但是仍无法解决连续性政策的评估问题。

2 哑变量面板模型

为了对连续性政策进行动态效果评价，本文构造政策哑变量面板模型，分别识别出各次政策的效果，有助于后续政策的有效制定。

记Y1it，Y0it为对应干预哑变量Dit取值的两个潜在结果，这时Xit是可以观测的混杂因素，Ui是不可以观测的混杂因素且不随时间变动。如果所有混杂因素可观测，那么条件独立性假设成立，即：进而下面式子成立：

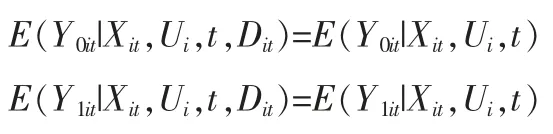
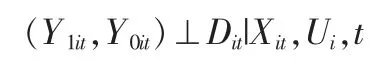
由此，以（Xit，Ui，t）为条件的干预组平均处理效应（ATT）为：

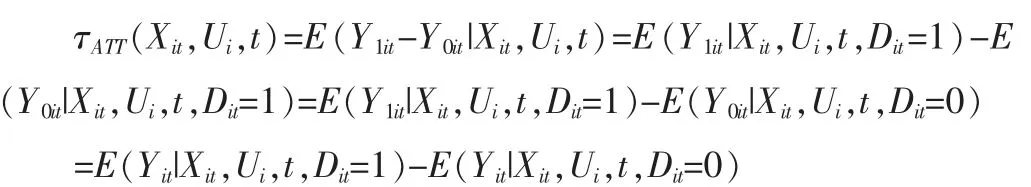
故如果混杂因素（Xit，Ui，t）可观测，理论上我们可以根据（Xit，Ui，t）的取值，对观测样本进行分组求和计算，然后根据（Xit，Ui，t）的取值概率Pr（Xit，Ui，t）进行加权求和，即可求得总体ATT 的估计值：

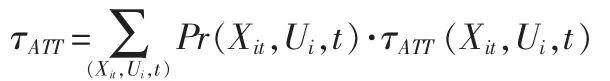
加入条件期望的线性假设：

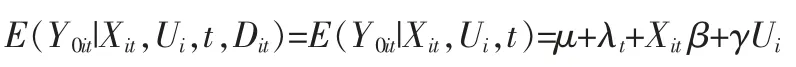
其中：λt为所有个体共同的时间变化趋势。

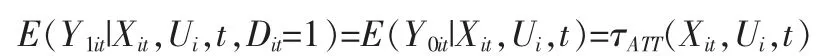
这时，观测值的条件期望为：

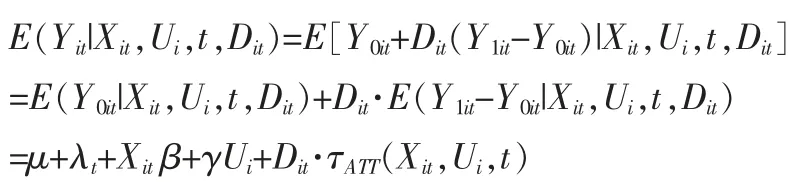
根据回归方程中的变量系数的含义，相应的回归方程为：

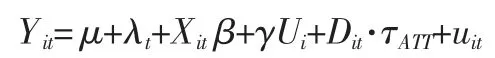
进一步定义个体异质性变量αi=μ+γUi，上面的回归方程变为：

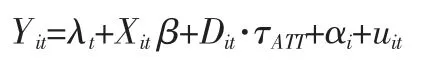
这就是一个典型的政策哑变量面板模型，考虑到个体异质性与回归变量的相关性，采用固定效应是适合的。政策哑变量前面的系数反映的即为总体ATT 值。

如果有k 个政策连续出台，相应设置k 个政策哑变量Dit1，进而得到连续政策评价模型：

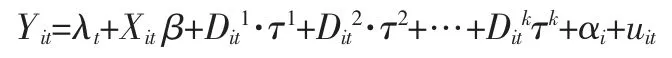
该模型可以对连续性政策进行动态效果评价。其中第k 个政策的有效性可以通过相应参数的显著性t－检验来识别。

该政策哑变量面板模型在进行政策评价时有如下优势。

（2）由于模型中存在非时变个体异质性，采用固定效应模型进行系数估计，可以在很大程度上控制政策选择的内生性问题。

（3）共同的时间变化趋势λ1可以采用设定不同时间的哑变量来替代。这些时间哑变量的加入，可以排除同时影响干预组样本与控制组样本的政策干扰，而这种情形在实证中是经常遇到的。

注意，政策哑变量面板模型的缺陷在于无法处理干预组单一样本问题。

3 结论

本文在系统梳理当前政策评价方法的基础上，构造出适于连续性政策评价的固定效应政策哑变量面板模型。该方法既可以动态识别单个政策的效果，也可以对混合政策效果的显著性进行检验，同时还可以在很大程度上控制政策选择的内生性问题，并可加入哑变量来控制整个宏观经济形势的影响。