考虑水流耦合效应的弧形闸门结构自振特性

2021-09-17丁俊丰翁光远张煜敏吴亚军

水利与建筑工程学报 2021年4期

丁俊丰，翁光远，张煜敏，吴亚军

(1.西安石油大学机械工程学院，陕西西安 710065；2.陕西省引汉济渭工程建设有限公司，陕西西安 710010)

大型水工弧形闸门结构构造复杂，且服役期间受环境激励、水流作用、洪水宣泄、引排水调控等因素的影响[1-2]，振动特性发生复杂变化，产生强烈振动现象，甚至引发闸门局部失效。如1995年7月，美国加利福尼亚州福尔瑟姆坝溢洪道闸门在例行开闸泄水过程中，闸门产生巨大振动，进而弧形闸门右支臂向内侧弯曲，闸门支铰铰轴被剪断，导致闸门破坏。针对大型复杂水闸结构的振动特性及共振问题，国内外学者开展了大量的理论分析和试验研究，取得了相应的研究成果[3-7]。付亮等[8]以湖南省柘溪水电厂7#和8#进水口工作闸门为研究对象，分析了闸门机组超负荷工作和高速水流导致闸门反向支撑损坏的安全隐患，并提出了相应的减震措施。李洪等[9]研究了汶川地震作用对紫平铺水利枢纽闸门影响和破坏，提出了闸门在地震发生时的应急抢救措施。文献[10]分析了角木塘水电站溢洪道表孔闸门的流激振动现象，研究了流激作用在弧形闸门上振动响应特性，改善了闸门的抗震性能。文献[11]以洹河景观水闸为研究对象，分别建立了流固耦合(FSI)与附加质量两种不同的固-液耦合形式的模型，提取结构固有模态，反映了水闸结构的工作特性和动力特性。文献[12]以某提灌工程输流管道为研究对象，对不同岔管接入角度模型进行流场分析，利用附加质量法建立流、固耦合模型，实现不同岔管接入角度的管道模态分析。文献[13]针对某农业灌区泄洪闸闸室静/动力稳定性问题，利用ANSYS建立三维模型，并计算闸室结构在有水、不考虑水流工况下静/动力特征。以上这些研究成果为闸门抗震设计提供了重要的理论依据，然而，在考虑水流-闸门相互作用的振动特性问题中，尚需要进一步开展理论分析、仿真模拟和现场实测[14-18]，本文以陕西省引汉济渭工程调水工程黄金峡水利枢纽的大型弧形钢制闸门为研究对象，设立不考虑水流、附加质量法考虑水流、流固耦合效应考虑水流3种模拟工况，研究弧形闸门在不同工况下的自振特性，为分析闸门的振动破坏机理及研究闸门-水流-地震相互作用提供了理论依据。

1 弧形闸门有限元模型结构

1.1 原型结构

引汉济渭工程是一项具有全局性、基础性、公益性、战略性的水利项目，对促进陕南循环经济，促进治理渭河水生态环境，推动全省实现区域协调可持续发展，具有十分重要的意义。黄金峡水利枢纽是引汉济渭工程重要的调水工程之一，采用的大型弧形钢制闸门具有启闭省力、运转可靠、闸墩厚度较小、泄流条件好等优点。弧形闸门结构复杂，工作时受水流冲击引发的闸门振动特性发生变化，为揭示水流对弧形闸门自振特性的影响，本文以黄金峡水利枢纽大型弧形钢制闸门为原型，采用ANSYS有限元软件建立计算模型结构，并结合现场实测，进行动力特性研究。该水闸结构主要由门叶结构、支臂桁架结构、支铰和链杆组成。支臂结构由上支臂结构和下支臂结构组成，上下支臂结构之间用横向桁架结构连接，增强水闸结构整体刚度，支臂结构一端用可转动支铰与闸墩结构连接，另一端采用连接件与门叶结构连接，弧形门叶为空心结构，门叶两侧与闸墩结构采用预埋钢制卡槽连接，形成门叶启闭的轨道，并设置止水装置。本文主要研究闸门结构考虑水流的自振特性，为了便于有限元建模和分析，因此，对黄金峡水利枢纽大型弧形闸门结构的细部构造进行了简化。

1.2 不考虑水流的弧形闸门有限元模型结构

利用Solidwork建立全尺寸黄金峡水利枢纽大型弧形闸门结构有限元仿真模型结构。模型结构主要分为门叶结构、支臂结构、支臂连接件、固定端铰支座和零件装配。

(1) 门叶结构。建立弧形闸门门叶结构，弧长为16 400 mm，半径为26 000 mm。选用Q345B钢材，面板加工厚度不小于25 mm，门叶厚度为2 000 mm，首先根据门叶结构的侧面平面图，通过拉伸建立门叶结构立体图，根据设计图纸及面板厚度，切除门叶部分实体单元，最后对弧形闸门门叶结构进行边界修正。

(2) 支臂结构。建立弧形闸门上下支臂结构，上支臂结构长为19 600 mm，下支臂结构与固定端相连长为24 000 mm，以门叶和支臂连接处为基准平面，建立支臂结构的平面图，通过拉伸相应长度建立上/下支臂结构实体单元，最后根据设计图纸对支臂结构进行抽壳，完成闸门支臂结构的建模工作。

(3) 支臂连接件。建立支臂结构横梁单元和次梁单元，以梁与门叶结构和支臂结构连接处为基准平面建立梁的平面图，通过拉伸相应的长度建立横/次梁的实体单元，由闸门的设计图纸对梁进行抽壳、倒角操作，完成闸门横/次梁连接件的建模工作。

(4) 固定端铰支座。闸门的铰支座分为上下两个支座，支座端的大小尺寸不同，根据闸门的设计图纸，建立闸门固定端上/下支座，通过拉伸、切除和倒角操作，完成闸门的铰支座建模工作。

(5) 零件装配。首先将以制作好的门叶结构、支臂结构和固定铰支座导入到Solidwork软件中，选用软件的装配体模块，对零件进行安装并给予各个装配体之间相应的约束(同心、固定、转动等)，最后将装配好的模型保存并退出。

图1为建立的黄金峡水利枢纽大型弧形闸门结构的全尺寸有限元仿真模型结构。该有限元模型结构使用Solid186单元进行建模，采用四面体和六面体网格进行剖分，网格总数为220 000，对闸门支臂端铰支座进行固定约束，弧形闸门两侧进行滑动约束，利用Modal模块进行弧形闸门模态分析模拟。闸门结构均采用Q345B钢材，弹性模量取2.01×1011Pa，泊松比为0.30。

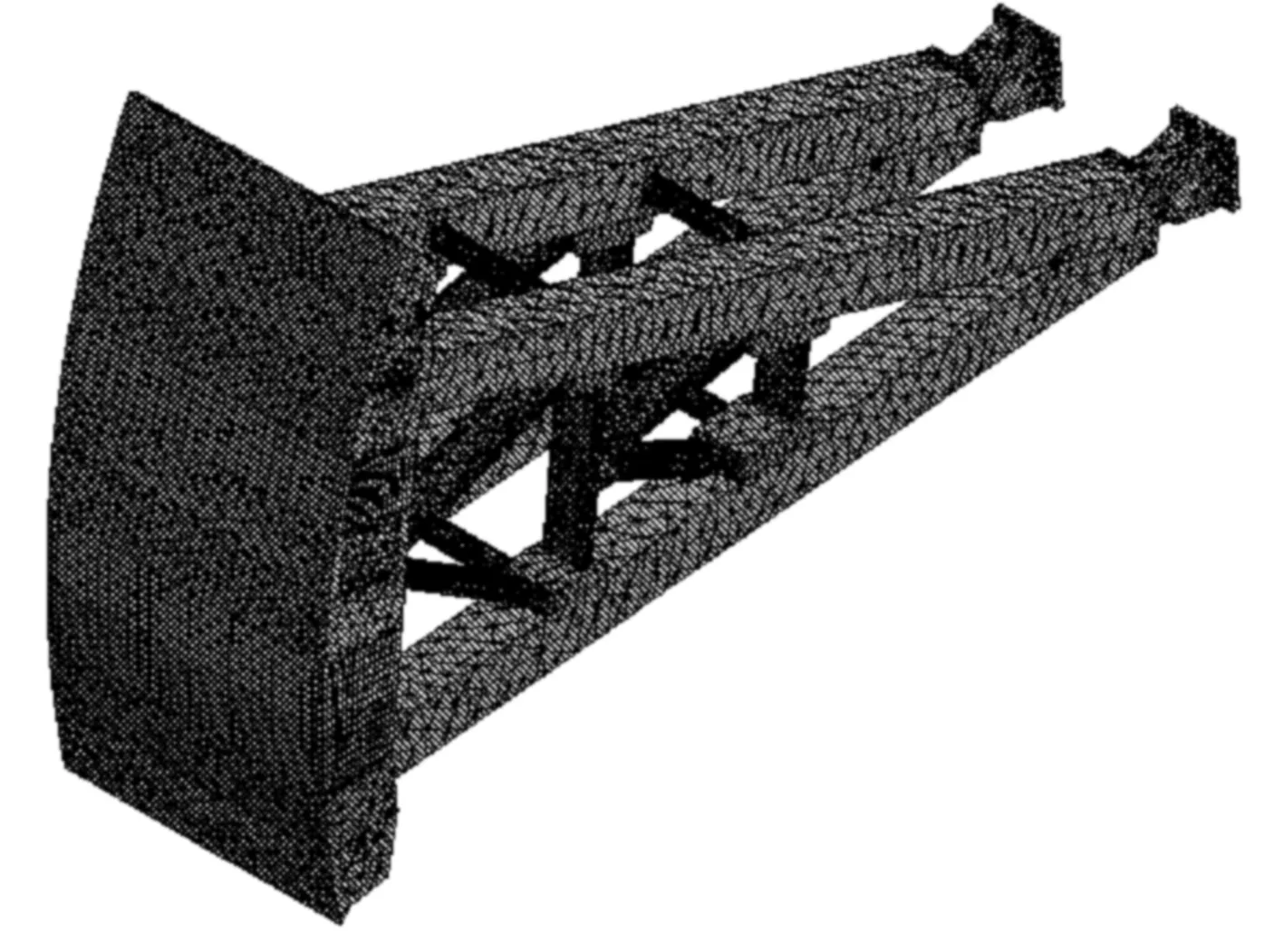
图1 全尺寸弧形闸门有限元模型结构

1.3 不同开度的弧形闸门有限元模型结构

考虑水流对弧形闸门结构自振特性的影响时，闸门开度是首先要考虑的因素之一。本文采用附加质量和流固耦合两种方法建立弧形闸门结构考虑水流的自振特性有限元计算分析模型，分别建立开度为0%、10%、20%、30%、40%、50%、60%、70%、80%、90%的水闸结构的附加质量有限元计算模型结构和流固耦合效应的有限元计算模型结构。

附加质量法是考虑流体介质与结构共同作用的自振特性分析的常用方法，在分析水体对闸门结构产生作用的过程中，为达到等效的动力响应，将动水压力以质量的形式施加在闸门结构上的一种分析方法，该方法是等效流体对闸门结构的作用因此误差较小，其中附加在结构上的质量的确定方法对模态计算和分析影响较大。本文按照参考文献[12]的方法计算考虑水流的弧形闸门的附加质量，在此理论基础上通过简化计算得出不同开度下水流的附加质量，每种开度工况对应的附加质量见表1。分别将每个开度对应的附加质量均匀施加在全尺寸弧形闸门有限元模型结构的门叶上，得到开度为0%、10%、20%、30%、40%、50%、60%、70%、80%、90%的附加质量有限元模型结构10种。

表1 不同工况的模型结构

直接将水流的附加质量均匀施加在门叶结构上的方法比较简便，但忽略了水流与闸门门叶之间的相互作用。本文利用ANSYS有限元软件的FLUENT-static structural-modal模块建立水流流体场和闸门结构考虑不同开度的流固耦合效应有限元计算模型结构，如图2所示。

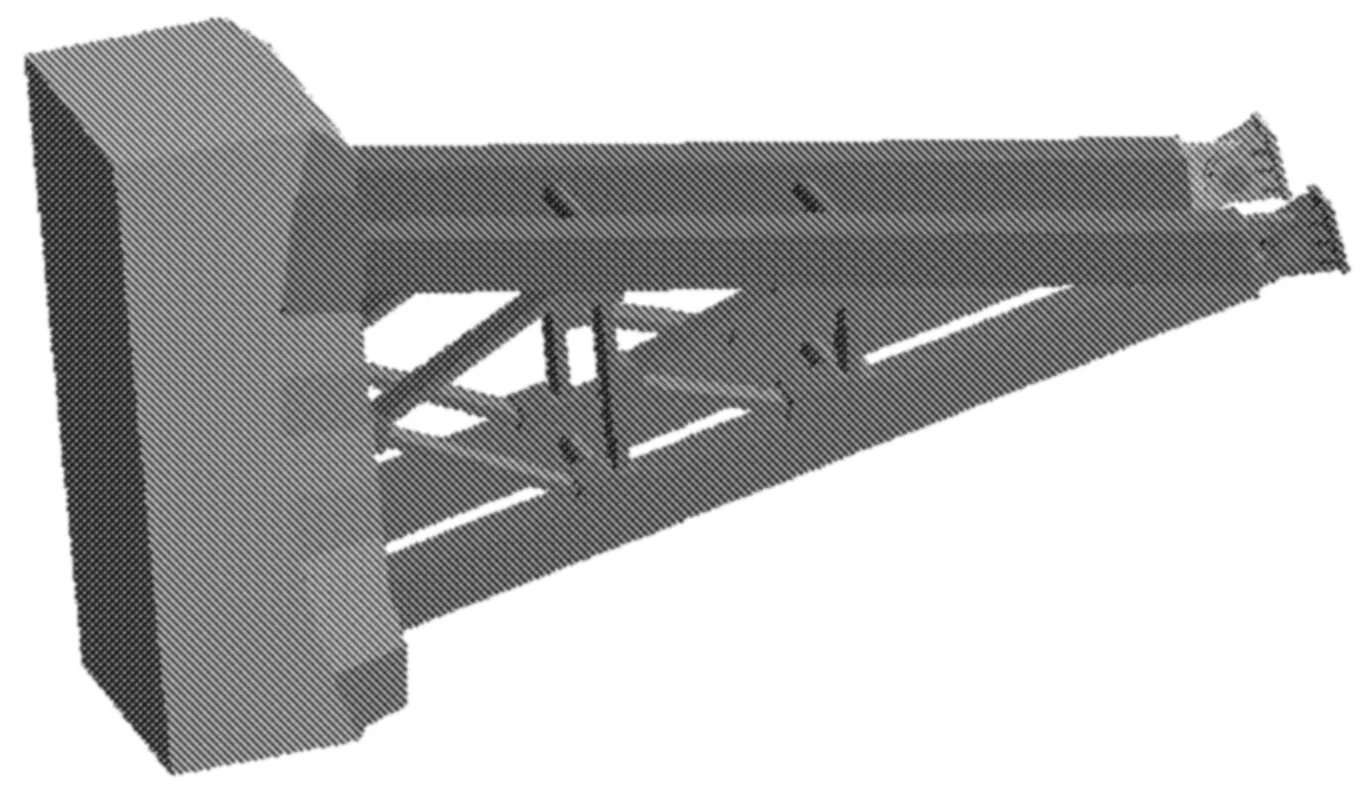
图2 考虑流固耦合效应的有限元模型结构

在不考虑水流的有限元模型结构的基础上，即图2所示的有限元模型结构的基础上，设置闸门结构水流影响的区域，图2中根据弧形闸门的形状、尺寸以及水流对闸门影响，经过计算得出闸门前5 m以外的水域对闸门影响较小，因此设置了闸门结构同高同宽、长度为5 m的水流域，水闸门叶迎水面与设置的流水域采用整体连接，水闸门支臂端处的铰支座采用固定约束，弧形闸门两侧设置成滑动约束，根据水流域内水位的高低来模拟水闸的不同开度，建立了开度为0%、10%、20%、30%、40%、50%、60%、70%、80%、90%的附加质量有限元模型结构10个。

本文建立了不考虑水流的有限元模型1个，不同开度的附加质量有限元模型10个，考虑流固耦合效应的有限元模型结构10个，分别对21个模型进行模态计算和分析。

2 结果分析

2.1 固有频率

2.1.1 闸门不开启的固有频率

分别对不考虑水流、附加质量、流固耦合效应的21个有限元模型结构进行模态计算和分析，提取了前20阶固有频率。不考虑水流的模型结构、开度为0%的附加质量模型结构、开度为0%的流固耦合模型结构的前20阶固有频率变化如图3所示。

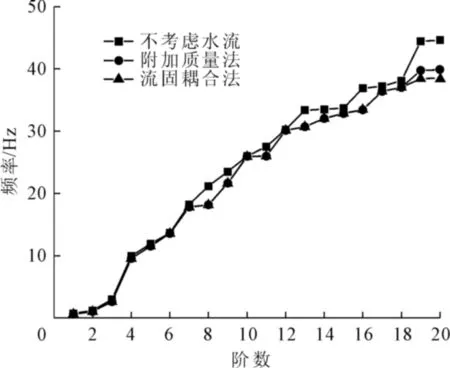
图3 弧形闸门不启闭的固有频率

由图3可以看出，水流对弧形闸门模型结构前6阶固有频率影响较小，在闸门结构振动情况相对简单的情况下，可忽略不计；第7阶以后的固有频率受水流影响较明显，用附加质量的方法和流固耦合的方法考虑水流对水闸结构自振特性的影响时，水闸结构的各阶固有频率较不考虑水流工况的模型结构对应的各阶固有频率呈下降趋势；附加质量的水闸模型结构和流固耦合的水闸模型结构的前18阶固有频率十分接近，图3中的曲线几乎是吻合的，从而说明，闸门振动相对复杂的情况下，采用附加质量的方法和考虑流固耦合效应的方法均能较好地揭示闸门结构的自振特性；当闸门结构振动情况特别复杂的情况下，采用附加质量法和考虑流固耦合效应的方法有着明显的差别，两种计算方法的最大差别为8.3%。复杂振动情况下，考虑水流与闸门之间相互耦合的作用，能更好地揭示闸门结构的自振特性。同时说明，当弧形闸门不开启时，水流对闸门自振特性有一定的影响，随着闸门开启，这种影响的机理更加复杂，泄洪时需要对闸门结构的自振特性进一步进行分析。

2.1.2 闸门启闭的固有频率

附加在闸门门叶的质量随着泄洪时闸门不同开度发生变化，流固耦合效应也随着闸门泄洪开度发生变化，因此，本文考虑了泄洪时闸门开度为10%、20%、30%、40%、50%、60%、70%、80%、90%的固有频率变化情况。采用附加质量的固有频率计算结果如图4所示。

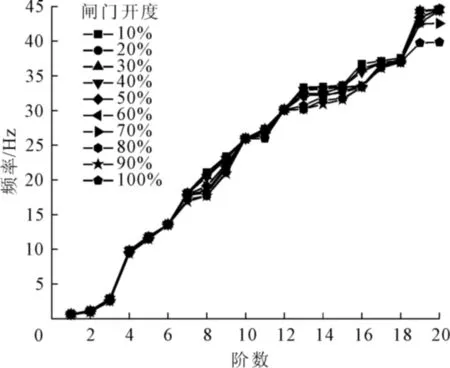
图4 不同开度附加质量的闸门固有频率

由图4可以看出，采用附加质量计算的闸门固有频率受泄洪时不同开度的影响，各阶固有频率随着闸门开度的增大呈现降低趋势，较不考虑泄洪开度影响的计算结果，闸门的固有频率下降的最大幅度为10.6%。同时，图4也表明了，闸门结构前6阶固有频率受水流影响较小，在振动不复杂的情况下，可以忽略水流对闸门结构自振特性的影响。

采用考虑流固耦合效应的有限元模型结构计算的闸门结构前20阶固有频率的结果如图5所示。图5表示了考虑流固耦合效应的不同开度闸门的固有频率。

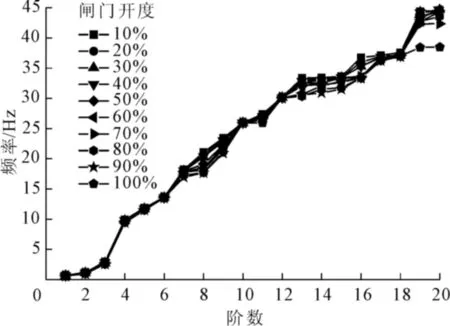
图5 流固耦合法闸门频率图

由图5可以看出，随着泄洪开度的增大，闸门结构的固有频率发生变化。当开度大于50%时，闸门结构的固有频率变化相对明显，以70%开度为例，和10%开度相比较，第20阶固有频率较附加质量下降了12.7%，开度为80%和90%时，第20阶固有频率较70%时都有所增大。从图5中的曲线可以看出，开度为70%时的固有频率变化较其他开度复杂，闸门结构在泄洪时，开度为70%时振动的情况更复杂。同时，通过对比图4和图5的计算结果可以发现，采用流固耦合效应的有限元模型结构分析闸门结构的自振特性时，固有频率的变化比附加质量的模型结构相对复杂，各阶固有频率频率既有呈下降趋势，也有呈增长趋势，水流和闸门之间的耦合效应对闸门结构的振动有一定的影响。

2.2 主要振型

2.2.1 不开启闸门的振型图

闸门开度为0%时，通过计算分析不考虑水流的有限元模型结构、附加质量有限元模型结构和流固耦合效应有限元模型结构，可以得到弧形闸门结构各种工况下对应的主振型频率和的主振型图。3种工况下，闸门不开启的主振型图相似，它们有着相同的变形特点。限于篇幅，以开度为0%，不考虑水流的有限元模型结构的振型图为例进行分析，图6给出了相应的振型图，其主振型频率为36.872 Hz。

图6 不开启闸门的振型图

由图6可以看出，在不考虑水流的工况下，闸门结构的整体变形呈现出对称性，门叶主要以发生弯曲变形为主，上支臂结构和下支臂结构分别在平面内发生了对称的弯曲变形，同时，支臂结构在振动中，伴随着扭转变形。

2.2.2 附加质量法闸门振型图

采用附加质量法对闸门进行模态分析，建立了不同附加质量的闸门结构有限元模型结构，假设水体为不可压缩性流体，水体的动力作用可以简化为在模型质量矩阵中加上附加质量矩阵。本文采用弧形水闸的附加质量有限元模型结构，模拟了闸门开度为10%、20%、30%、40%、50%、60%、70%、80%、90%等9种状态下的自振特征，提取了前20阶振型图。通过分析主要振型图，附加质量有限元模型结构在闸门不同开度下，对应的振型图相似，用附加质量考虑水流影响时，弧形闸门结构自振特征基本相同。限于篇幅，并结合前文分析，开度为70%时，自振情况相对复杂，因此，本节以开度为70%的附加质量有限元模型结构主要振型图为例，进行分析，相应的振型图如图7所示。闸门的主振型频率为30.705 Hz。

图7 附加质量有限元模型闸门结构振型图

由图7可以看出，采用附加质量有限元模型结构分析不同开度闸门结构自振特征时，附加质量对各阶振型有明显的影响，附加质量的弧形闸门结构的各阶振型变形在附加质量影响下不是完全对称的，在主振型图中，闸门门叶结构发生波浪式振动，门叶最大的弯曲位移发生在中间部位，靠近边缘位置，弯曲变形的位移达到了最大。上支臂结构和下支臂结构的变形以弯曲和扭转组合变形为主，对比图6和图7的主要振型，可以看出，附加质量对支臂结构振动的影响小于对闸门门叶结构的影响。

2.2.3 考虑流固耦合作用闸门振型图

泄洪时，闸门结构所处的水流环境，除水流质量发生变化外，水流速度变化引起作用在门叶结构的动水压力发生变化，从而影响闸门结构自振特性。本文采用弧形水闸的流固耦合效应有限元模型结构，模拟了闸门开度为10%、20%、30%、40%、50%、60%、70%、80%、90%等9种状态下的自振特征，提取了前20阶振型图。通过分析主要振型图，考虑流固耦合效应的有限元模型结构，在闸门不同开度下对应的振型图基本相似。限于篇幅，本节主要以开度为70%的考虑流固耦合效应有限元模型结构振型图为例进行分析，相应的振型图如图8所示。闸门的主振型频率为25.889 Hz。

图8 流固耦合下的闸门结构振型图

由图8可以看出，水流在闸门结构门叶上产生的水压力对闸门结构整体的自振特性有明显的影响。门叶部位的弯曲变形较附加质量模型结构更加明显，弯曲变形产生的最大位移位于门叶中间部位；上支臂结构和下支臂结构的弯曲变形较附加质量模型结构更大，其扭转变形下的最大扭转角位移位于支臂结构与闸墩固结的三分之一位置处，同时，支臂结构之间的连接构件产生较大的振动变形，在此类闸门结构设计时，应予以足够的重视。