基于有限元法的尾矿坝边坡三维稳定分析

苏振宁，邵龙潭

(大连理工大学 工业装备结构分析国家重点实验室， 辽宁 大连 116024)

尾矿库具有体量大，危险性高，失稳破坏性强等特点，是重大危险源之一。合理保障尾矿坝的稳定性和耐久性，对于保障矿业可持续生产，保证库区下游的生产生活具有重要的工程价值。对尾矿坝边坡一般选取典型断面以平面应变问题形式利用极限平衡法或强度折减法进行稳定分析[1-5]。但尾矿库一般为建于山谷中的典型三维结构体，二维稳定分析不能真实反映尾矿坝的稳定性。

陈顺良等[6]采用三维有限元分析了尾砂开采对坝体位移和应力的影响。邓红卫等[7]建立三维数值模型，采用渗流-应力耦合机理，研究了干滩长度对尾矿库坝体稳定性的影响。李洪梁等[8]利用无人机测量采集数据，建立三维模型计算浸润线分布，采用极限平衡法分析坝体稳定性。以上研究均对尾矿坝建立了三维模型，但稳定性仅采用定性的应力分析或二维安全系数结果。采用三维流固耦合模型有限元强度折减法能计算尾矿坝三维稳定安全系数从而对稳定性进行分析[9-10]，还能对尾矿坝三维失稳形态进行研究[11]。但有限元强度折减法存在边坡稳定判据影响安全系数的问题[12]，并且尾矿坝为非均质复杂边坡，能否对所有土层采用同一折减系数仍有待研究[2]。

有限元极限平衡法[13]根据“真实”应力场结果和基于极限平衡状态的安全系数定义，可以采用优化算法搜索区域内的临界滑动面。于斯滢等[2]采用二维有限元极限平衡法分析了尾矿坝稳定性，取得了很好的效果。三维有限元极限平衡法[14]同样具备计算效率高，无需折减迭代计算，滑动面和安全系数明确的特点，能给出局部安全系数分布，能为尾矿坝安全设计提供可靠依据和技术支持。本文即采用三维有限元极限平衡法对所研究的尾矿坝边坡开展三维稳定分析，并与有限元强度折减法的分析结果相比较，以期更好指导工程实践。

1 边坡稳定分析方法

1.1 二维极限平衡法

根据《尾矿库安全技术规程》[15](AQ 2006—2005)要求对典型断面使用瑞典圆弧法和Bishop法判断坝体稳定性。本文选取尾矿坝最大断面分别采用瑞典圆弧法、Bishop法和Morgenstern-Price(M-P)法计算安全系数。瑞典圆弧法和Bishop法要求滑动面为圆形；M-P法满足整体和每个土条的力与力矩平衡可适用于任意形状的滑动面。极限平衡法计算软件采用GeoStudio。

1.2 三维有限元强度折减法

有限元强度折减法在有限元计算过程中不断将土体的强度参数进行折减，直至边坡到达临界状态。当边坡达到临界状态时，强度参数的折减系数也就是安全系数。该安全系数表征着材料的强度储备，基于摩尔-库仑强度准则的强度折减法表达式为：

(1)

式中：c为土体黏聚力；φ为土体摩擦角；K为强度参数折减系数，当边坡达到临界状态，K即为安全系数。

在存在渗流的尾矿坝稳定分析中，有限元强度折减可采用流固耦合模型，进行渗流计算。强度折减法不需要提前设定滑动面，可通过临界状态时位移增量云图直接判定滑动面。

1.3 三维有限元极限平衡法

三维有限元极限平衡法基于“真实”的有限元应力场，有限元计算采用弹塑性-流固耦合模型，在计算中无需折减土体强度参数。该方法通过构造三角形网格滑动面，在有限元应力场的基础上根据整体安全系数定义计算滑动面安全系数，并通过优化方法寻找区域内最小安全系数以及其所对应的滑动面。该方法优点在于采用真实应力场计算，无需迭代计算，没有收敛性问题，物理意义明确，能给出准确的最危险滑动面和对应的安全系数以及滑动面局部安全系数分布，计算简单易于推广和工程应用。本文采用MATLAB软件编写了三维有限元极限平衡法程序，用以计算尾矿坝边坡安全系数。有限元极限平衡法由以下三个部分组成：

1.3.1 安全系数定义

三维有限元极限平衡法局部安全系数和整体安全系数分别被定义为：

(2)

(3)

式中：d为滑动面上滑动方向；τf为抗滑剪应力矢量，方向与滑动方向d相反，其值根据摩尔库仑强度准则计算；τ为滑动面上剪应力矢量；s为滑动面面积。局部安全系数是抗剪应力与剪应力在滑动方向上的投影的比值，其物理意义是一点在滑动方向上距离极限平衡状态的衡量。通过边坡整体极限平衡条件和积分中值定理[13]，可得整体安全系数，其表征滑动面上各点局部安全系数的中值。

对于存在孔隙水压力的边坡的稳定分析，强度计算应采用基于有效应力的方法，摩尔-库仑强度准则为：

τf=σ′tanφ′+c′

(4)

式中：σ′为滑动面上的有效正应力；φ′为有效摩擦角；c′为有效黏聚力。

有限元在流固耦合计算中应力采用的是有效应力与孔隙水压力相结合的形式。所以从有限元中导出的应力就是有效应力，可以使用式(3)直接计算。只需保证强度参数为有效应力强度参数。

1.3.2 滑动面构造

根据定义式(3)，有限元极限平衡法需要对滑动面上的变量进行积分，数值积分需要对积分域进行离散，采用三角形网格形式对滑动面进行划分。

采用改进椭球形表征滑动面。相比于使用圆心坐标(x，y，z)和三轴半径(a，b，c)作为参数的传统椭球滑动面，改进椭球形滑动面参数增加了椭球面绕z轴的旋转角度α和中间柱体宽度l，如图1所示。考虑到实际工程中受地形以及建模方向影响，椭球形滑动面的水平主轴方向未必是x和y坐标轴方向，所以增加了旋转角度α。在三维问题中，当边坡沿垂直于坡体断面方向延伸，边坡的安全系数越趋近于二维平面应变结果，其滑动面也更趋近于管状。所以增加了中间柱体宽度l。

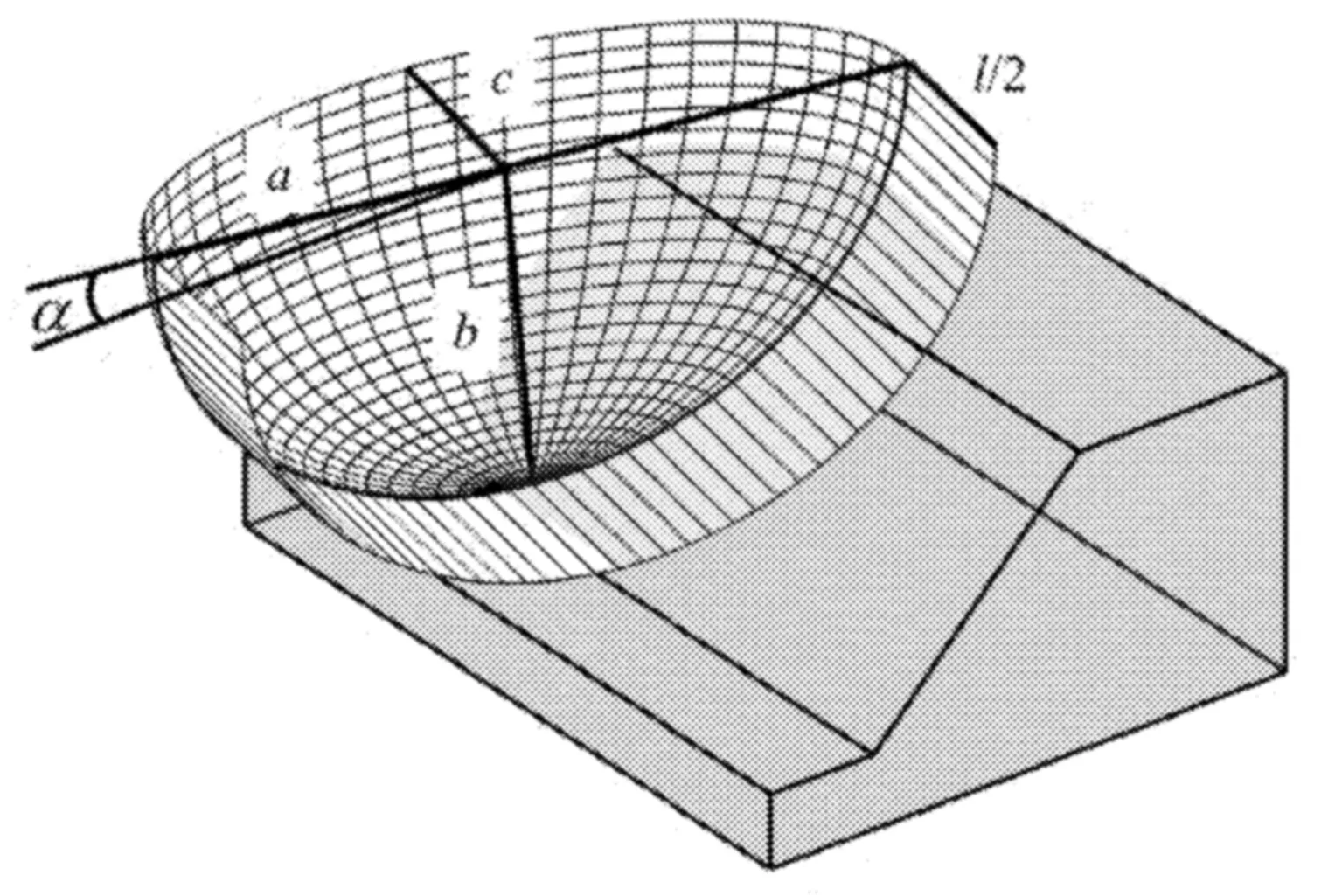
图1 改进椭球形滑动面

1.3.3 最危险滑动面搜索

三维有限元极限平衡法的滑动面搜索方法选择粒子群算法作为优化方法。粒子群算法是一种智能优化算法，具有良好的计算性能和出色的应用效果，在边坡最危险滑动面的搜索中有良好的效果[16]。

本文使用MATLAB的全局优化工具箱进行粒子群算法的最危险滑动面搜索，改进椭球形滑动面参数作为搜索参数，整体安全系数作为目标函数，具体流程见图2。

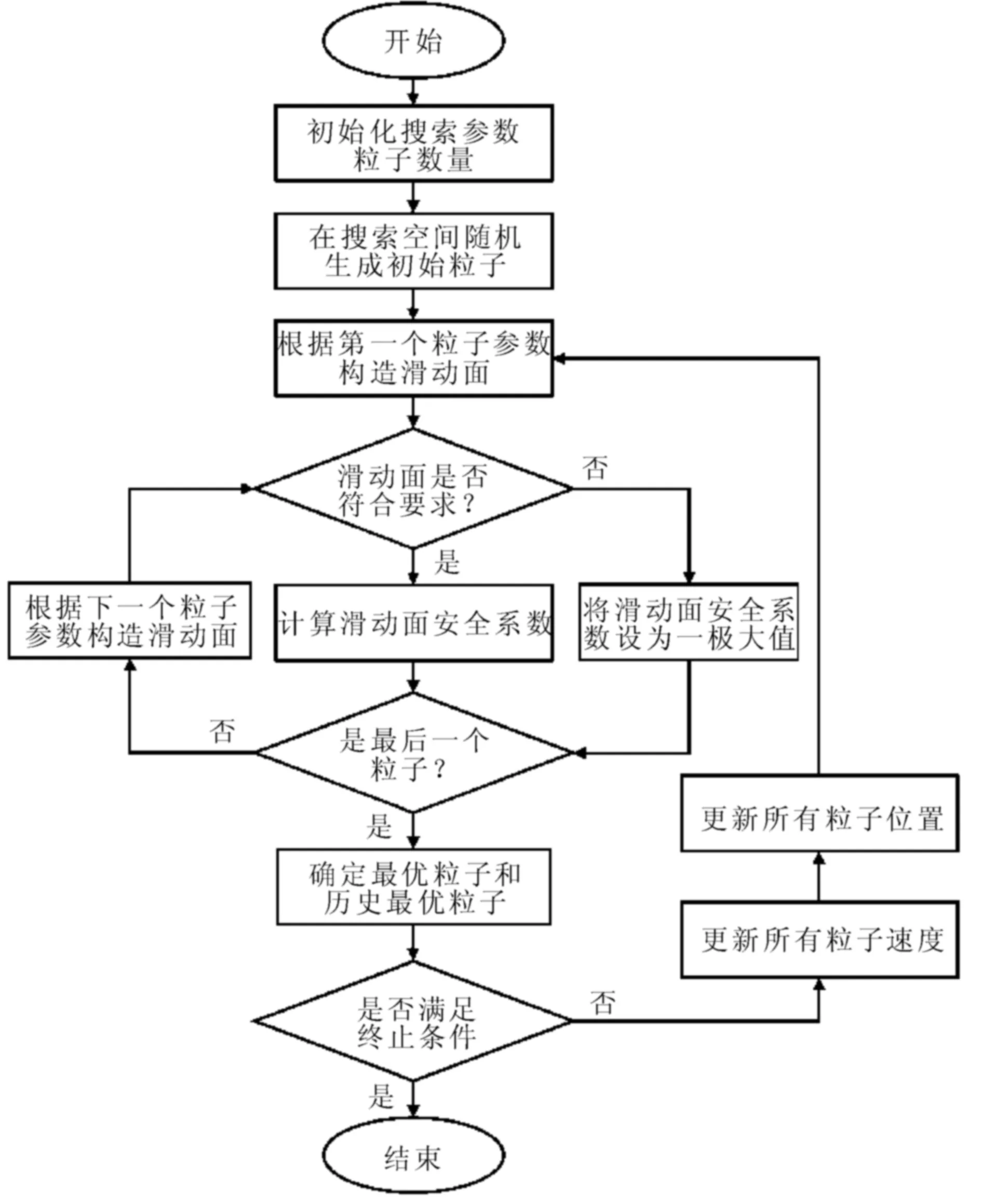
图2 粒子群算法流程图

2 尾矿库三维计算模型

2.1 工程概况

某待建尾矿库采用上游筑坝法建设工艺，库区内汇水面积8.9 km2，平均坡度达到8.92%，沟长约3.68 km。初期坝坝址选择在沟口处，初期坝采用库内开采的风化岩石筑透水坝，顶宽6 m，内外坡均为1∶2，坝顶标高1 665 m，坝底标高1 615 m，最大坝高50.0 m。后期子坝坝采用尾矿加高，坡比1∶5.0，终期标高为1 813 m，总坝高198 m。当坝高达到最终堆积标高1 813 m标高时，为二等尾矿库。

为确保坝体的渗透稳定，降低浸润线，初期坝顶以上每升高15 m，增设水平排渗盲沟，尾矿堆积坝上共需设9条水平排渗盲沟。排渗盲沟与堆积坝坝面水平距离为175 m。排渗盲沟由水平排渗盲沟和垂直盲沟的导水管组成，盲沟在尾矿沉积滩上开挖，平行坝轴线，每50 m盲沟设一条导水管，盲沟由反滤料外包土工布组成。

2.2 尾矿库有限元模型

尾矿料的物理力学性质和尾矿库堆积材料的概化分层根据相同矿区另一尾矿库勘察资料和工程经验综合确定。因为矿物开采自统一矿区且采用相同的选矿工艺，所以此勘察可以作为新建尾矿库中尾矿料参数的取值依据。尾矿材料分为尾粉砂，尾粉土和尾粉质黏土(见表1)。尾矿库区地形特征和尾矿材料概化分层，以及排渗盲沟设计建立尾矿库几何模型如图3所示，其中A-A是所考察的典型断面位置。

表1 尾矿材料计算参数表

图3 尾矿库几何模型

二维模型采用GeoStudio软件分析，稳态渗流计算采用SEEP/W模块，极限平衡法安全系数计算采用SLOPE/W模块。三维模型采用ABAQUS软件进行流固耦合计算。尾矿库内上游根据不同干滩长度设置水压边界条件，水压力设为0 kPa，排渗盲沟和初期坝设置自由渗出边界。初期坝和尾粉砂设置为非饱和状态下的参数，尾矿库底部为约束位移边界条件，采用摩尔库仑强度准则。计算分别采用三种工况：(1) 不考虑渗流的工况；(2) 洪水工况设计干滩长度是100 m；(3) 正常生产工况设计干滩长度是200 m。

3 计算结果

3.1 渗流计算对比

将三维与二维渗流计算结果在断面处对比，如图4所示。根据计算，在洪水工况下，三维和二维计算得到的浸润线未触及靠近坡顶的两条排渗盲沟。在正常工况下，三维浸润线触及靠近初期坝的四条排渗盲沟，二维浸润线均未触及排渗盲沟。同时，在两种情况下，靠近初期坝位置和初期坝内，二维计算浸润线埋深大于三维结果。造成以上情况的原因是随着靠近下游方向，谷口过水面积减小，二维分析无法反映这一特性，造成浸润线埋深较深。渗流计算结果显示，排渗盲沟是确保浸润线埋深的关键构造措施，此尾矿库管理应加强排渗盲沟的监控，确保排渗通畅。

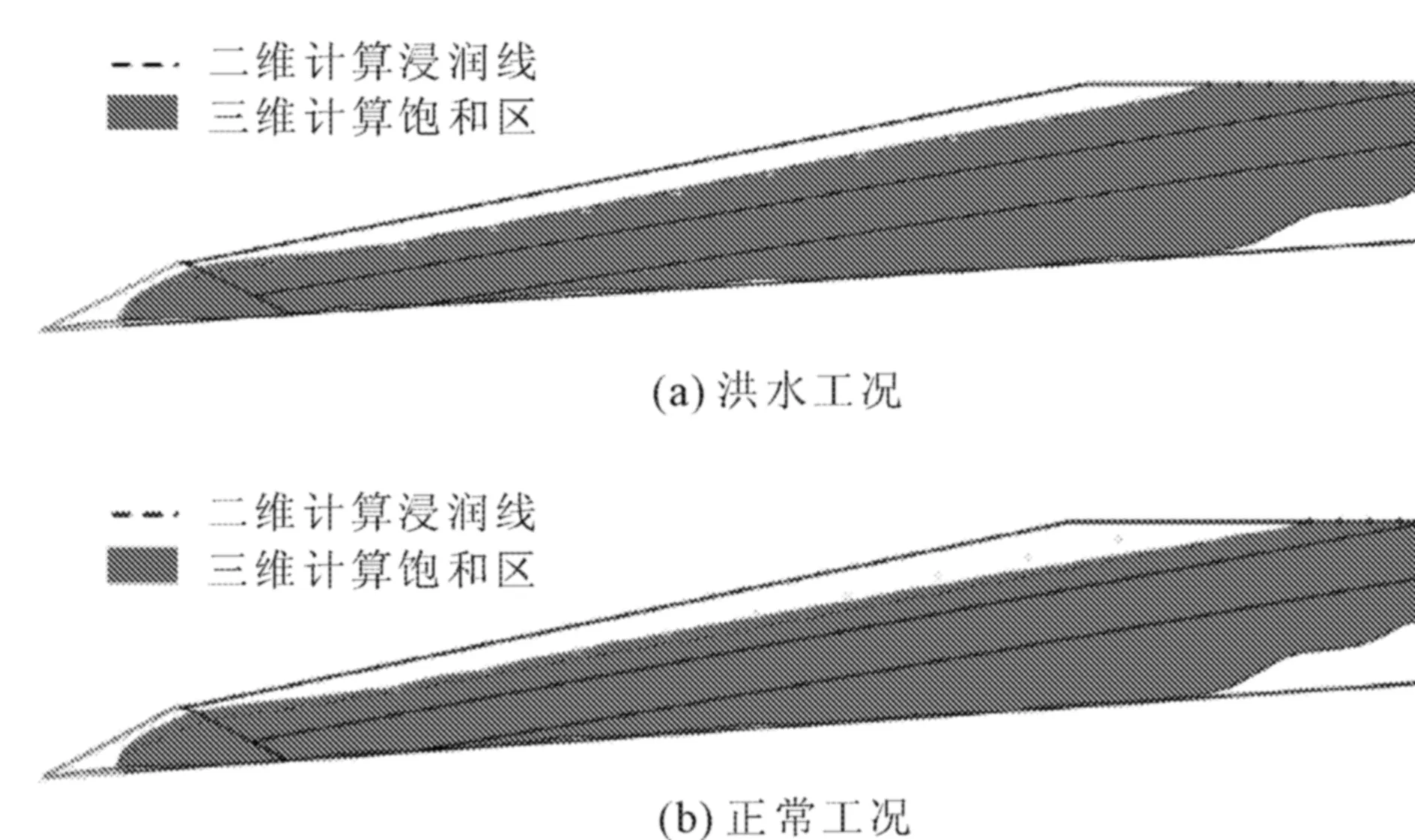
图4 二维与三维尾矿库渗流场计算结果

3.2 稳定性计算结果对比

3.2.1 二维极限平衡法

二维极限平衡法计算结果列于表2中，滑动面如图5所示。三种计算方法中，M-P法的安全系数最小，这是因为M-P法不要求滑动面为球形滑动面。与M-P法相比Bishop法误差在8.3%～11.8%之间，瑞典圆弧法误差在0.9%～5.1%之间。二维计算结果均满足规范要求。从滑动面可见，M-P法计算得到的滑动面位于下层尾粉质黏土区域面积大，因为尾粉质黏土与其他尾矿料相比强度参数更低。

图5 正常工况尾矿库断面位置的滑动面比较

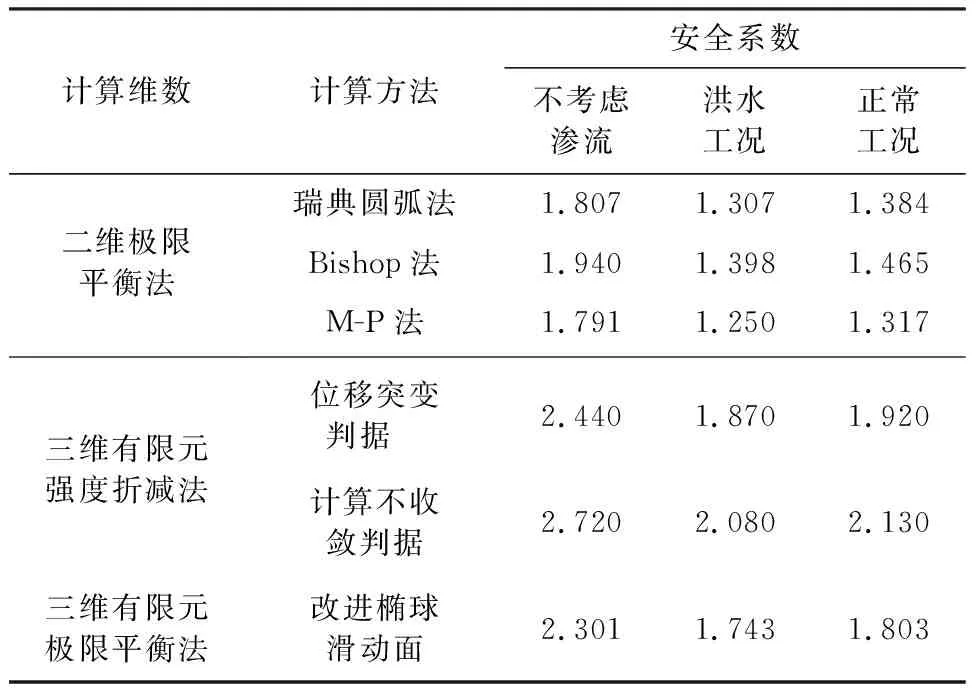
表2 不同方法安全系数比较

3.2.2 三维有限元强度折减法

不考虑渗流以及洪水工况和正常工况下，边坡的破坏形式与滑动区域相似，所以取正常工况为例进行分析。图6(a)为计算断面处以计算不收敛的前一个增量步的位移增量云图表示的滑动面俯视图。

图6 正常工况滑动区域俯视图

根据以往的研究[12]，采用特征点位移突变时的强度折减系数作为安全系数，是一种合理的有限元强度折减法失稳判据。因为尾矿坝破坏模式导致特征点位移曲线相对平滑，突变点不明显。将计算不收敛时x方向位移最大的点作为判断位移突变的特征点，正常工况下特征点的水平位移与折减系数关系如图7所示，水平位移与折减系数具有不同单位，不能直接判断突变点，将两者关系绘制于方形区域，并计算曲线段中的斜率变化角，将斜率变化角的极小值点作为水平位移的拐点。这种方法虽然获得的拐点位置，但仍添加了人为因素(选择方形区域绘制曲线)。根据这种方法计算得到的安全系数列于表2中，表2中同样列出了以计算不收敛作为失稳判据的安全系数，后者相对于前者的误差在11.2%～11.5%。

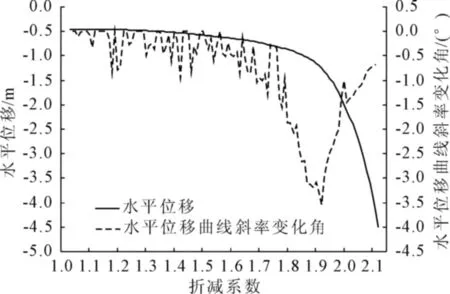
图7 根据特征点位移突变判据计算安全系数

3.2.3 三维有限元极限平衡法

三维有限元极限平衡法搜索得到的滑动区域如图6(b)所示，安全系数列于表2中。有限元极限平衡法滑动面是改进椭球形，当椭球形底部超过模型区域，滑动面会自动调整回模型底部，所以在图4中滑动面断面并非椭圆，而是与二维M-P法优化得到的滑动面形状相似。三维有限元极限平衡法能计算局部安全系数，图8为正常工况下的局部安全系数分布云图，图中可见不同材料强度参数对局部安全系数的影响，尾矿库区模型底部的几何也会对局部安全数产生影响。滑动面底部的局部安全系数最小，靠近初期坝位置有最大的局部安全系数，说明此处具有较大的安全余量。

图8 正常工况滑动面局部安全系数

3.2.4 对比分析

渗流会导致安全系数减小，二维极限平衡法中考虑渗流的影响要大于三维有限元方法。

三维有限元方法的安全系数要大于二维极限平衡法安全系数，有限元强度折减法安全系数要大于有限元极限平衡法安全系数。有限元强度折减法的安全系数相对偏于危险，尤其是采用不收敛作为判据时得到的安全系数。

在滑动面方面，图4和图6显示了三维有限元强度折减法和三维有限元极限平衡法滑动区域以及滑动深度相似，在考察断面，三维方法与M-P法也基本一致，仅在滑动面的滑入位置存在略微差异。

有限元强度折减法在确定精确的安全系数和滑动面都存在问题，并且尾矿库内材料复杂非均质，对不同土层采用同样的折减系数存在争议。有限元极限平衡法能准确的给出滑动面和对应的安全系数，并且还能对局部安全系数进行考察。两种方法能相互印证，互为补充，可以更好的分析尾矿坝的三维稳定性问题。

4 结 论

对某尾矿库进行三维数值建模，并在此基础上采用有限元极限平衡法和有限元强度折减对尾矿坝进行三维稳定性分析，并与二维极限平衡法结果进行了对比，具体结论如下：

(1) 三维稳定分析方法相比于二维方法，能反映三维地形和三维渗流场对稳定性的影响，避免了典型断面选取对计算的影响。三维有限元极限平衡法和有限元强度折减法计算结果显示尾矿坝溃坝呈现深层滑动整体破坏形式，得到尾矿坝破坏范围近似椭球形。

(2) 三维有限元极限平衡法根据其安全系数定义式能给出明确的安全系数和对应的临界滑动面，解决了强度折减法中存在的对尾矿坝边坡不同土层采用同一折减系数是否合理以及安全系数难以准确判定等问题。三维有限元极限平衡法还能显示出局部安全系数，更有利于指导工程实践。

在实际工程中建议使用三维有限元极限平衡和有限元强度折减法相结合，综合判断尾矿坝的稳定性。