花岗岩残积土中砾石颗粒的二维形状特征及其簇重构
2021-09-17关振长何亚军
关振长,何亚军,高 翔,邓 涛
(福州大学 土木工程学院, 福建 福州 350116)
花岗岩残积土由花岗岩母岩长期受物理、化学风化作用形成,在我国华东、华南地区有着广泛分布。花岗岩残积土的矿物成分多样、细观结构复杂,尤其是其砾石成分的形状特征对花岗岩残积土工程性质有重要影响[1-3]。因此,准确描述砾石颗粒的形状特征,是描述此类土体细观力学特性,构建宏观本构模型的关键。
李晶晶等[4]采用图像测量与处理技术,对四种不同类型粗骨料的轮廓形状、棱角性和表面纹理等形状特征进行量化研究。Wang等[5]通过数字图像处理技术获得了珊瑚砂的二维颗粒图像特征,运用数理统计和分形理论探讨了颗粒尺寸和分布特征对颗粒形状参数的影响。陈建湟等[6]基于图像处理技术探讨了矿物颗粒的球度、凸度和长宽比等形状特征。Maroof等[7]通过CT扫描获取颗粒三维形状轮廓,并基于球度比理论,对颗粒形状进行定量表征与分类。
近年来,基于颗粒形状特征统计和傅里叶描述子实现簇重构的方法,逐渐开始运用于离散元数值模拟中。丁珣昊[8]通过AIMS扫描建立粗集料形状样本库,并在颗粒形态特征量化分析的基础上遴选典型颗粒,实现其在PFC中的二维簇重构。林渝轲[9]和王雪奎等[10]通过图像处理技术分别获取道砟与黏土颗粒形状,统计分析了颗粒的宏细观形状特征参数,实现了颗粒形状特征量化分析。聂志红等[11]通过AIMS集料图像测量系统获取了道砟颗粒磨损前后的形状特征,分析道砟劣化过程中的级配和形状特征的变化。付茹等[12]通过CT扫描与图像处理技术获取花岗岩砂性残积土颗粒的球度、圆度等形状参数,并基于谐函数对砂粒进行重构。徐长文等[13]通过显微镜光学成像、数字图像处理方法获取了不同粒径区间颗粒的最大轮廓投影,分析了粗粒土的傅里叶描述子与粒径的关系。Yang等[14]基于图像处理技术,量化描述颗粒形状特征参数(伸长、球形、凹凸度和粗糙度),探讨了尾矿与天然砂的物理力学性质的差异。周剑等[15]通过CT扫描获取岩石颗粒的初始形状,并结合FDEM模拟颗粒的断裂和破碎,分析了岩石颗粒初始形状对其破碎的影响。
在前人研究基础上,本文通过图像分析法得到闽南地区典型花岗岩残积土中砾石颗粒的二维形状轮廓,进而对其形状特征进行量化统计分析,并据此对颗粒形状展开定量分类。进一步地,根据颗粒一维线轮廓的傅里叶描述子与形状相似度分析,遴选典型砾石颗粒并在PFC平台实现砾石颗粒的簇重构。
1 砾石颗粒形状的图像分析法
1.1 闽南地区典型花岗岩残积土的颗粒级配
花岗岩残积土在我国华东、华南地区有着广泛分布,以厦蓉高速公路扩建工程漳州段为典型代表,其花岗岩残积土的颗粒级配曲线如图1所示,其不均匀系数Cu=5.57、曲率系数Cc=1.12。对大量土样进行观测后,发现小于5 mm的颗粒基本趋于球形,形状特征不显著;因此本文仅针对最小粒径>5 mm(过5 mm筛后)的砾石成分展开细致研究。选取现场砾石颗粒200个,其部分颗粒如图2所示。
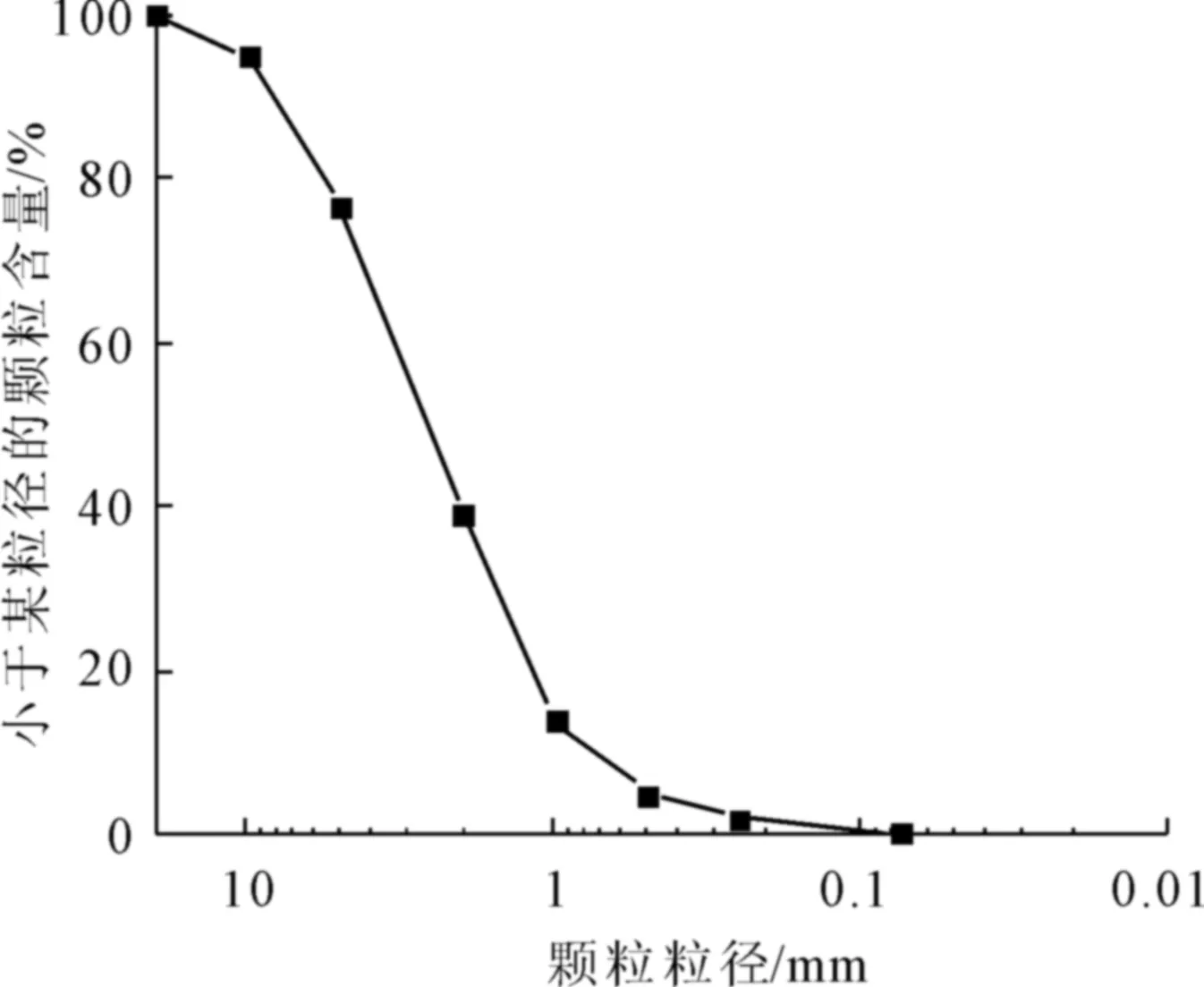
图1 花岗岩残积土的级配曲线

图2 花岗岩残积土中的砾石颗粒
1.2 图像分析法的基本流程
为了避免颗粒的阴影和表面纹理等不良影响因素对颗粒外轮廓的提取造成不良影响,设计了一种逆光箱装置来进行图像拍摄采集,如图3所示。将获得的二维图像通过去噪、阈值分割、边缘检测等算法处理,最终获得上述200个砾石颗粒的轮廓曲线,部分如图4所示。

图3 逆光箱装置

图4 砾石颗粒轮廓曲线
2 砾石颗粒二维形状特征的描述
砾石颗粒的形状特征具体包括形态、棱角性及表面纹理。形态是从宏观层面来描述颗粒整体的外轮廓变化;棱角性参数属于介观层面,表示整体外轮廓在角点处的变化剧烈程度;表面纹理属于颗粒局部的细观层面,反映颗粒表面的裂隙分布和粗糙性。除基本几何参数外,本文还引入若干高阶量化指标,来统计分析砾石颗粒的形状特征,如表1所示。

表1 砾石颗粒形状特征的描述
3 砾石颗粒二维形状特征的统计分析
3.1 高阶量化指标的统计分析
图像分析法获取了200个砾石颗粒的高阶量化指标,对其作直方图统计,如图5所示。进一步采用高斯概率密度函数对直方图进行拟合,如图5中虚线所示。得到各高阶量化指标的均值MN、标准差SD、分布区间,以及频数分布曲线的偏度SK和峰度KU,汇总于表2。

图5 高阶量化指标的统计直方图

表2 高阶量化指标的统计汇总
长细比AR反映颗粒形状轮廓偏离针状的程度,圆度RN反映颗粒形状轮廓偏离圆状的程度;特别地,标准圆的AR与RN均为1。由表2可知,AR、RN的主要分布区间分别为1.2~2.8、1.4~2.0,其均值分别为1.810、1.617,且均为右(正)偏态分布,表明实际砾石颗粒形状具有一定的狭长特征,但其长细比指标、圆度指标不会过大(分别不超过3.0与2.0),这是由于过长过细的砾石颗粒在自然堆积的过程中易发生破碎。
粗糙度C反映颗粒表面的粗糙程度,矩形度BL反映颗粒的饱满程度/棱角性;特别地,标准圆C与BL分别为1.000和0.785。由表2可知,C为右(正)偏态分布,而BL为左(负)偏态分布;粗糙度与矩形度中位数偏离标准圆的程度较小,表明具有狭长特征的砾石颗粒在运动过程中,由于不断碰撞、摩擦等作用导致颗粒表面棱角性减弱,进而不断变得平滑。
3.2 高阶量化指标与基本几何参数的相关性
进一步地,探讨高阶量化指标与基本几何参数之间的相关性。绘制高阶指标AR、RN、C和BL与基本几何参数Dfmax和d之间的散点图,进而根据散点分布趋势,采用合适的曲线方程对其进行拟合;各拟合曲线的相关系数汇总于表3。
由表3可知,长细比AR与费雷特最大直径Dfmax之间,矩形度BL与等效短轴d之间有较为显著的相关性,其散点图及拟合曲线如图6所示。需要说明的是,相关性分析前须对200个散点数据进行预分组处理。以图6(a)为例,按0.5 mm间隔,把Dfmax值从6.5 mm到17.5 mm分为22组;各组内求得其AR值的平均,进而绘制散点图并采用二次曲线拟合。
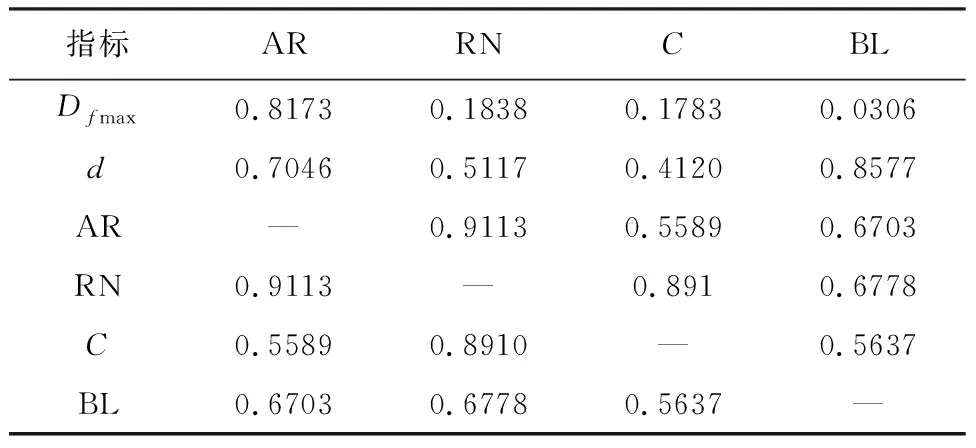
表3 各形状特征参数之间的相关系数
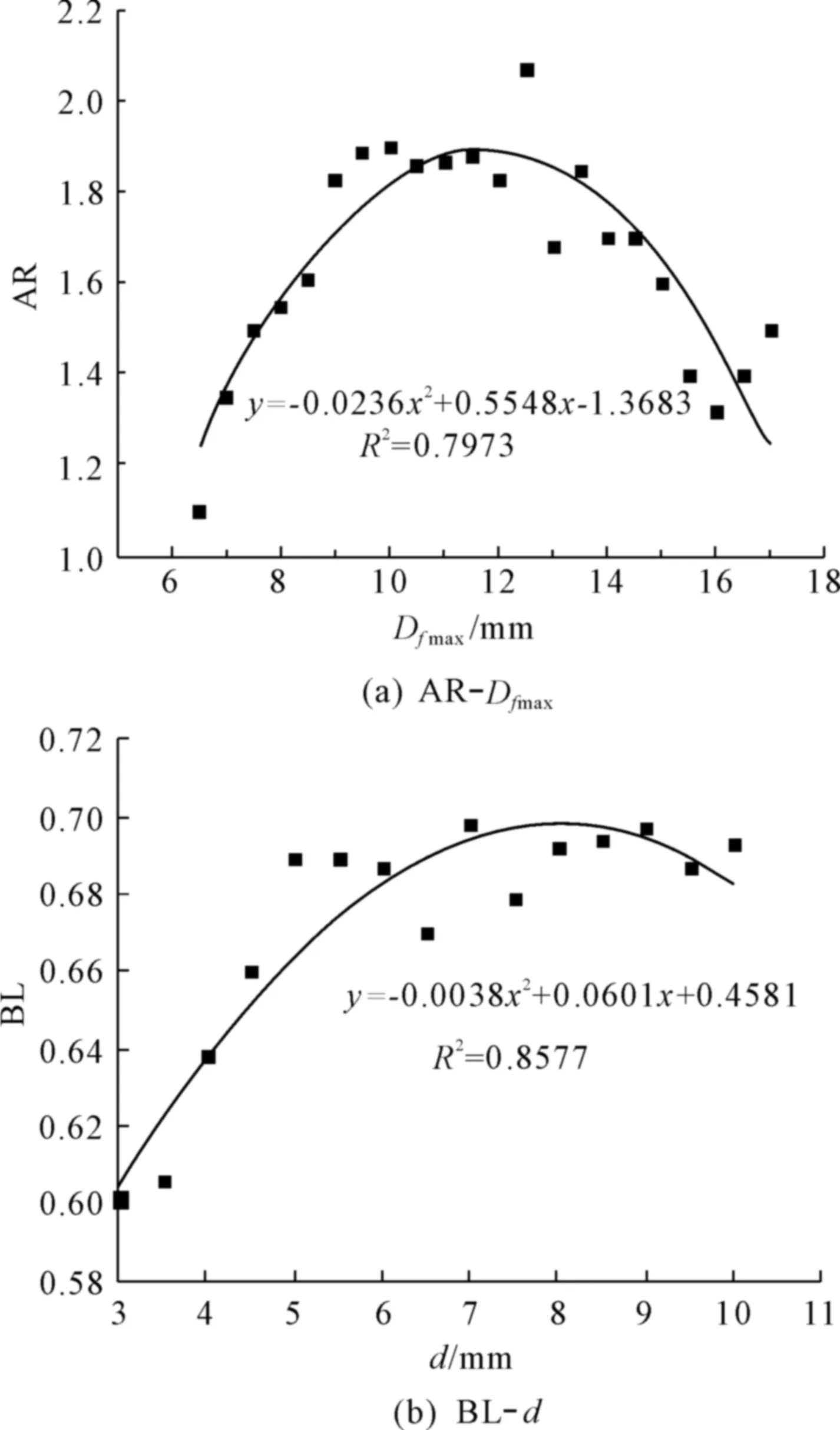
图6 高阶量化指标与基本几何参数之间的相关性
由图6(a)可知,随着Dfmax的增加,AR呈先增大后减小的变化趋势,较大或者较小粒径颗粒的长细比不会太大,其最大值出现在中位数12.2 mm附近,表明砾石颗粒的狭长形状特征在粒径区间两端逐渐弱化。
由图6(b)可知,BL随着d的增加先陡增而后趋于平缓;当d值小于5 mm时,其颗粒多呈现弯曲或中间大两头小的形状,当d值大于5 mm后,颗粒形状逐渐趋于球形。
3.3 高阶量化指标之间的相关性
类似地,探讨四个高阶量化指标之间的相关性。绘制高阶量化指标AR、RN、C、BL之间的散点图,根据散点分布趋势,采用合适的曲线方程对其进行拟合。各拟合曲线的相关系数汇总于表3中,可知长细比AR与圆度RN之间,圆度RN与粗糙度C之间有较为显著的相关性,其散点图与拟合曲线方程如图7所示。

图7 高阶量化指标之间的相关性
由图7可知,长细比AR和粗糙度C均随着圆度RN的增加大致呈线性增长。更为重要的是,RN与AR分别表示颗粒是否为针状和轮廓偏离圆的程度,且二者具有良好的线性相关特性(或者说线性可分特性),因此可将上述两个高阶量化指标作为后续颗粒分类的重要依据。
3.4 砾石颗粒形状的定量分类
通常可将砾石颗粒形状分为三种基本类型:类球形、半球形半棱形和类棱角形[17]。由于高阶量化指标RN与AR之间具有显著的线性相关性,可将其作为颗粒分类的重要依据。绘制200个颗粒的RN-AR散点图,如图8所示(部分颗粒有重叠);进而确定两条临界直线(有一定主观性),可将散点图分为类球形、半球形半棱形和类棱角形三大区域。上述方法为砾石颗粒形状划分提供了定量依据。

图8 砾石颗粒RN-AR的散点图
4 砾石颗粒的簇重构
离散元数值模拟中,簇颗粒形状对含砾花岗岩残积土数值模拟的真实性有重要影响,既往采用概化几何形状随机生成的簇颗粒,不能准确反映花岗岩残积土砾石颗粒的形状特征。在砾石颗粒形状特征的统计分析基础上,进一步构建花岗岩残积土砾石颗粒样本库,遴选典型颗粒形状,在PFC平台上对其进行簇颗粒重构[16]。具体步骤如下:
Step1:通过图像分析法得到200个颗粒的二维面轮廓,并将二维面轮廓转化为一维线轮廓函数。
Step2:针对单个颗粒,其一维线轮廓函数可以采用傅里叶级数进行拟合,即得到该颗粒的n阶傅里叶系数,进而以上述傅里叶系数构成列向量,作为该颗粒一维线轮廓的傅里叶描述子f。同理可得到200个砾石颗粒的一维线轮廓傅里叶描述子。
Step3:依据RN与AR,对前述200个砾石颗粒进行预分组,共分成60组别,并对每组颗粒占比进行统计。认为占比<1%的组别为次要组别(不进行典型颗粒遴选),最终得到25个主要组别,其占比如图9所示。
Step4:基于一维线轮廓的傅里叶描述子f,采用有限维向量相似的方法,对各组内颗粒进行形状相似度分析。形状相似度Da的值越大,说明该颗粒与同组别颗粒的相似程度越高,越能代表本组别的其他颗粒。最终遴选了25个典型砾石颗粒,作为25个组别的典型代表,如图9所示。
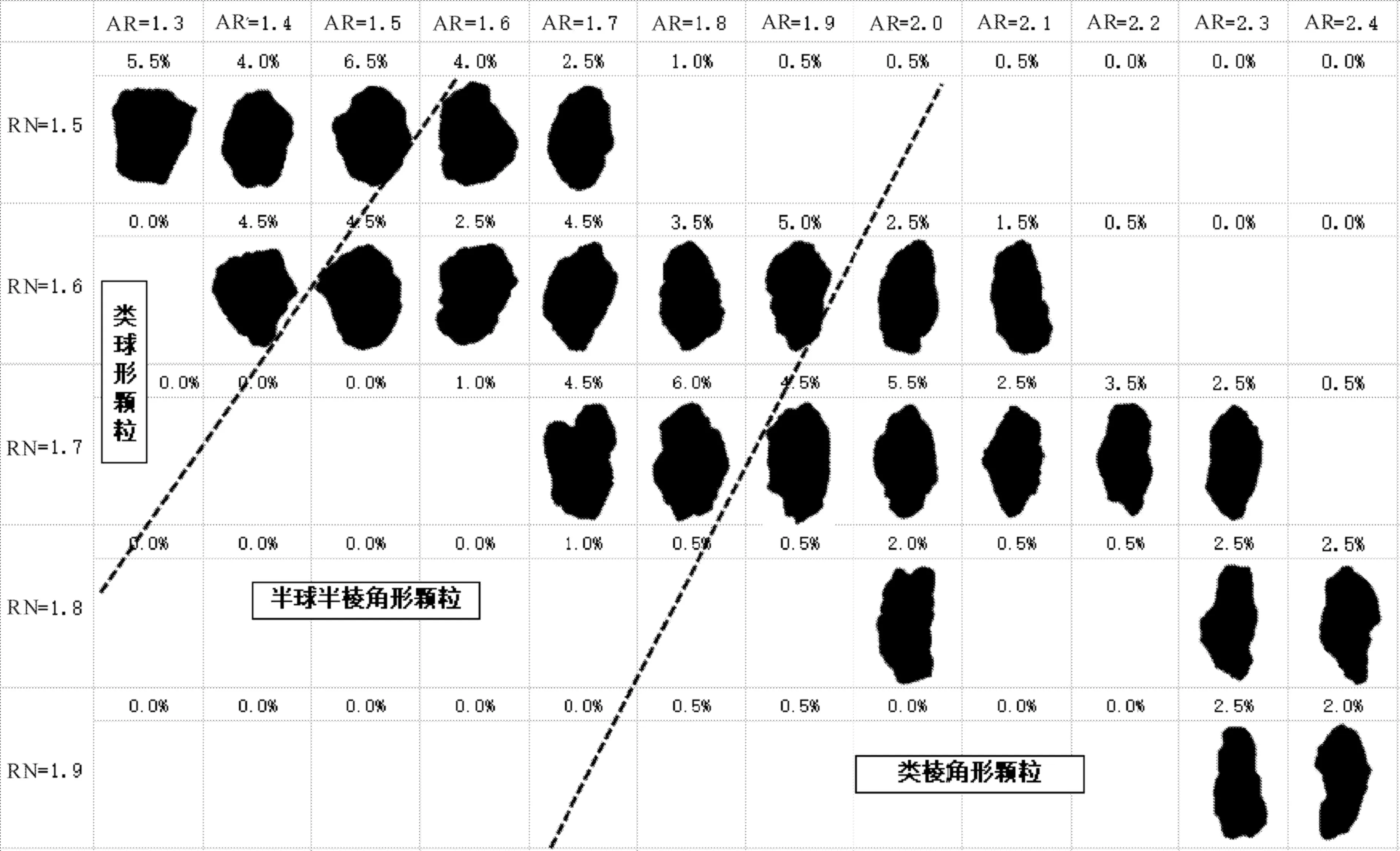
图9 典型砾石颗粒(25种)及其分类
Step5:根据遴选所得25个典型砾石颗粒的一维线轮廓傅里叶描述子f,在AutoCAD平台绘制其二维面轮廓,并分别保存为25个dxf文件。将上述dxf文件导入PFC平台,根据典型颗粒的二维面轮廓,由PFC中clump算法,对砾石颗粒进行簇重构,其结果如图10所示。

图10 典型砾石颗粒(25种)在PFC中的簇重构
依据上述步骤实现典型砾石颗粒的簇重构,为后续建立花岗岩残积土的精细化离散元数值模型,研究花岗岩残积土的宏/细观力学特性提供了基础支撑。
5 结 论
以闽南地区典型花岗岩残积土中的砾石颗粒为对象,首先通过图像分析法得到其颗粒的二维形状轮廓,进而引入一系列基本几何参数和高阶量化指标,来定量描述颗粒的二维形状特征;并在PFC平台实现典型砾石颗粒的簇重构。研究所得主要结论如下:
(1) 砾石颗粒的高阶量化指标的统计直方图表明,砾石颗粒形状具有一定的狭长特征,且过长过细的砾石颗粒在自然堆积的过程中会发生破碎,对其进行曲线拟合后,发现AR、RN和C为右偏态分布,而BL为左偏态分布,具有狭长特征的砾石颗粒在运动过程中,由于不断碰撞、摩擦等作用导致颗粒表面变得平滑。
(2) 高阶量化指标与基本几何参数的相关性分析表明,长细比AR随最大费雷特直径Dfmax呈先增大后减小的变化趋势,颗粒狭长的形状特征在粒径区间两端逐渐弱化;而矩形度BL随着等效短轴d的增加先急剧增大而后趋于平缓,小粒径颗粒多呈现弯曲或中间大两头小的形状,大粒径颗粒形状逐渐趋于球形。
(3) 圆度RN与长细比AR之间具有较为显著的线性相关性,因此可进一步通过两条临界直线,将颗粒形状定量地分为类球形、半球形半棱形和类棱形三大类。
(4) 通过颗粒一维线轮廓的傅里叶描述子与形状相似度分析,遴选了25种典型砾石颗粒,并在PFC平台实现砾石颗粒的簇重构;为后续建立花岗岩残积土的精细化离散元数值模型,研究花岗岩残积土的细观力学特性提供了基础支撑。
