非智力因素对初中学生数学问题提出能力的影响研究

向兴　彭乃霞　马威

[摘 要]数学问题提出能力是学生需要掌握的必备技能之一，非智力因素对其具有较大的影响作用。以都匀市七、八年级的学生为研究对象，采用问卷调查法，了解都匀市初中学生非智力因素和数学问题提出能力概况，并探讨都匀市初中学生的非智力因素对数学问题提出能力的影响。研究发现：都匀市初中学生的非智力因素处于中等偏上水平，数学问题提出能力处于中等水平;学生的非智力因素及其各维度与数学问题提出能力呈显著正相关，其中学习兴趣、学习习惯和自我效能感对学生的数学问题提出能力影响最大。因此，教师在教学过程中应培养学生的数学学习兴趣、良好的学习习惯、正确的自我效能感，提高学生的课堂参与，以此来培养学生的数学问题提出能力。

[关键词]非智力因素;数学问题提出能力;相关性分析

[中图分类号]G633.6[文献标识码]A[文章编号]1005-4634（2021）05-0081-07

1 问题提出

培养学生的创新思维是社会发展的需要。学生能否提出有价值的数学问题是学生具备创新思维的关键。教育部在2011年颁布的《义务教育数学课程标准》中对“提出问题”进行了落实，要求学生要“初步学会从数学的角度发现问题和提出问题，综合运用数学知识解决简单的实际问题，增强应用意识，提高实践能力”^[1]。2017年颁布的《普通高中数学课程标准》更是以提高学生从数学角度发现和提出问题的能力作为本课程的目标，其中还将提出问题作为六大核心素养的主要表现^[2]。由此可见，培养学生的数学问题提出能力是落实我国课程标准的基本途径之一。数学问题提出能力是指个体在数学学习过程中或在实际生活中能发现并提出具有一定价值的数学问题的综合素质。非智力因素是指除去包括观察力、记忆力、注意力和想象力等认知能力以外的一切因素，包括兴趣、动机、意志、信念、习惯和性格等，它们都会不同程度地对学生的学习起着调控作用。国内外有关问题提出能力的研究，主要有问题提出和问题解决的关系探讨、问题提出能力的培养策略研究、问题提出能力的评价研究和问题提出能力的影响因素研究。关于问题提出能力的影响因素方面，国内外大多研究者仅从学生的智力因素方面考虑其对学生问题提出能力的影响，从非智力因素方面探讨其影响的研究还比较匮乏。

因此，本研究以贵州省都匀市的初中学生为调查对象，了解都匀市初中学生的非智力因素和数学问题提出能力概况，探讨都匀市初中学生的非智力因素对数学问题提出能力的影响，以期获得关于培养学生数学问题提出能力的建议和对策。

2 研究设计

2.1 调查研究设计

研究选取都匀市内的初中学校（黔南师院附中、都匀三中、都匀十中、都匀五中、匀东中学）为调查基地，在各个学校的七、八年级分别随机选取两个班的全体学生作为调查对象。（由于调查所占学生课堂时间较长，且考虑到九年级学生的学业负担较重，研究未选取九年级学生作为被试）。本次调查共发放问卷1 000份，回收964份，剔除无效试卷121份，剩余有效试卷843份，有效回收率为87.4%，将所得数据录入EXCEL和SPSS25.0中进行分析。

2.2 研究工具

第一，非智力因素量表。本研究中的初中生非智力因素量表主要参照彭乃霞^[3]教授的《非智力因素调查问卷》和王光明^[4]教授的《非智力因素特征调查问卷》，并结合都匀市初中学生的特征进行改编，主要包含非智力因素中的学习兴趣、学习动机、学习习惯、学习信念、学习焦虑和自我效能感，共72题。采用利克特态度5级评分法，選择“非常符合”得5分、“符合”得4分、“基本符合”得3分、“不符合”得2分、“非常不符合”得1分，反向题与之相反，以平均分作为最后得分，共计30分。参照中学生非智力因素中数学焦虑的分法^[5]，将非智力因素及各维度（学习兴趣、学习动机、学习习惯、学习信念、学习焦虑、自我效能感）划分为3个等级。10分以下为非智力因素较低水平，记为等级1;11～20之间为非智力因素中等水平，记为等级2;21～30分之间为非智力因素较高水平，记为等级3。

第二，数学问题提出能力测试卷。本研究中的测试卷主要参考天津师范大学王蕾、西南大学蒋秋的硕士毕业论文以及蔡金法等人的研究成果进行改编，涵盖了初中的代数、几何、统计3个内容，并要求学生根据已有的问题情境尽可能多地从数学的角度提出数学问题，且无需对提出的问题作出回答。评价标准主要参照夏小刚等人编制的“学生提出问题能力”的评价量表^[6]、高岱亮等人编制的“提出问题能力”的PTA量表^[7]和徐斌艳等人在“数学问题提出”能力上的水平分层主张^[8]，从提出问题的数量、种类、创新性3个方面进行改编。具体见表1。

2.3 信效度分析

为检验量表所得数据的可靠性，本研究在回收初测卷后用SPSS25.0对非智力因素量表和数学问题提出能力测试卷的信效度进行分析。结果显示，问卷总信度系数为0.941，其中非智力因素量表信度系数为0.942，数学问题提出能力测试卷信度系数为0.614，数据表明问卷总体可信。此外，为检验问卷的效度，本研究采用“KMO”和巴特利特球形进行检测，得出KMO的值为0.775>0.7，P值0.000<0.001，巴特利特球形检验通过，表明问卷数据适合做因子分析。从以上数据可知，问卷的信效度较为理想，即问卷能有效地反映学生的非智力因素水平和数学问题提出能力，可以进行大面积实测。

3 调查数据分析

3.1 非智力因素概况分析

第一，非智力因素得分分析。数据结果显示（见表2），本次被试学生的非智力因素最高得分28分，最低11分，平均分为20.23，说明被试中大部分学生的非智力因素处于中等偏上水平。

第二，非智力因素等级分析。从表3中可知，被试学生中处于中等水平的占全体学生的47.2%，较高水平的占全体学生的52.7%，说明都匀市初中学生的非智力因素水平中等偏上。这是由于调查的学生大多数居住在都匀市内，家庭经济条件、受教育质量、生活环境相对较好。因此，学生的非智力因素水平较高。

第三，非智力因素各维度得分分析。非智力因素调查量表中各个维度总分为5分，从表4中可知，被试学生的非智力因素各个维度的平均值在3.176～3.865之间，说明被试学生的学习兴趣、学习动机、学习习惯、学习信念、学习焦虑和自我效能感都处于中等水平。通过各维度的平均值可看出，自我效能感的平均值为3.176，相较于其他几个维度来说处于较低水平。综合各方面分析，这是由于七年级学生刚从小学升入初中，出现知识难度、学习方式、环境变化等方面的不适应，造成学生的自我效能感低下。而八年级学生从代数知识转到学习几何知识，知识类型在变化，以至于學生的自我效能感较低。

3.2 数学问题提出能力概况分析

第一，数学问题提出能力得分分析。本研究中的数学问题提出能力测试卷总分为10.2分，0～3.4为数学问题提出能力较低水平（等级1），3.5～6.8之间为数学问题提出能力中等水平（等级2），6.9～10.2为数学问题提出能力较高水平（等级3）。根据表5中的数据结果显示，本次被试学生的数学问题提出能力最高得分9.2分，最低3.6分，平均分为6.496分，说明被试的学生大部分数学问题提出能力处于中等水平。

第二，数学问题提出能力等级分析。根据表6中的数据显示，被试学生的数学问题提出能力处于中等水平的占全体学生的52%，较高水平的占47.9%，说明都匀市初中学生的数学问题提出能力处于中等偏上。

第三，数学问题提出能力各指标得分分析。测试卷总共3道题，按照评分标准，问题的数量总分为12，问题的种类总分为9，问题的创新性得分为9。表7数据显示，问题的数量平均值为10.63，最小值为5，最大值为12;问题的种类平均值为4.5，最小值为2，最大值为8;问题的创新性平均值为2.23，最大值为7，最小值为0。说明大部分被试学生能提出一定数量的问题，但在提出问题的种类和创新性上还需加强。

3.3 非智力因素对数学问题提出能力的影响

第一，初中生非智力因素与数学问题提出能力的相关性分析。“衡量事物之间，或称变量之间线性相关程度的强弱并用适当的指标表示出来，这个过程就是相关分析。”^[9]为探讨初中生非智力因素与数学问题提出能力之间的相关性，研究主要采用等级变量的相关分析，与其相对应的相关系数是斯皮尔曼（Spearman）等级相关系数。根据非智力因素等级与数学问题提出能力等级的相关分析结果可知，学生的非智力因素及各个维度与数学问题提出能力之间相关性显著（见表8）。其中非智力的各维度对数学问题提出能力影响由高到低依次为：自我效能感、学习习惯、学习兴趣、学习动机、学习焦虑和学习信念。

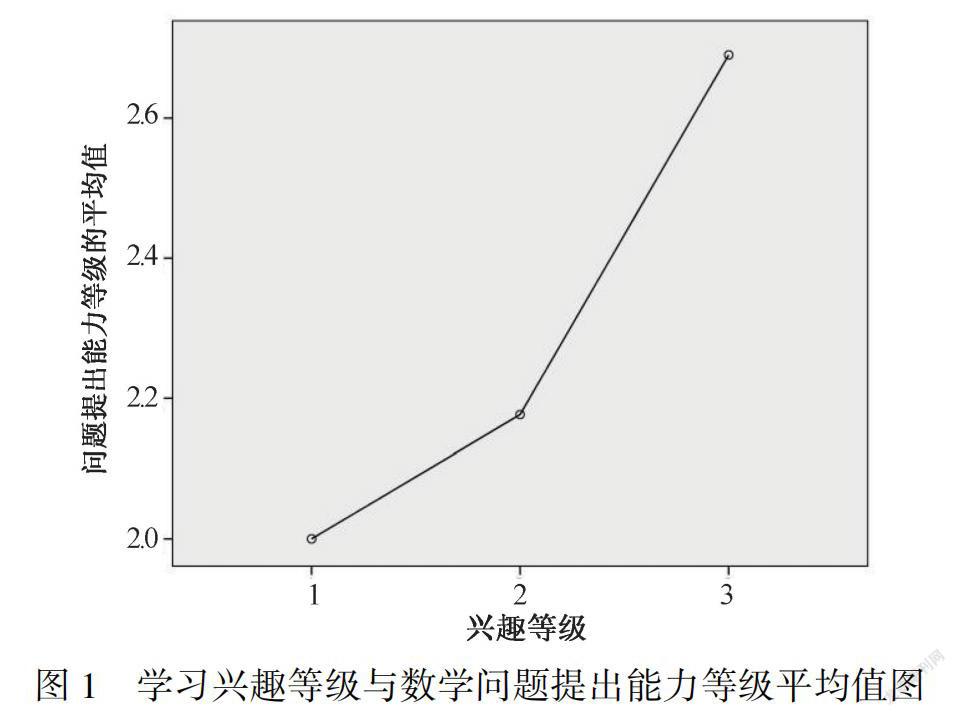
第二，学习兴趣与数学问题提出能力。从表9中可知，sig.=0.000<0.05，由此验证，学生的学习兴趣对数学问题提出能力有一定的影响作用。

从图1中可知，学生的学习兴趣越浓厚，其数学问题提出能力越强。因此，教师在进行数学问题提出能力的培养时，应注重从学生的学习兴趣入手，激发学生提问的兴趣。

第三，学习动机与数学问题提出能力。从表10中可知，sig.=0.000<0.05，由此验证，学生的学习动机对数学问题提出能力有一定的影响。

从图2中可知，学生的学习动机越强，其数学问题提出能力越好。也就是说，动机是学生提出数学问题的原动力。因此，在课堂教学过程中，教师应激发学生的学习动机，促使学生进行思考质疑，提出数学问题。

第四，学习习惯与数学问题提出能力。从表11中可知，sig.=0.000<0.05。由此验证，学生的学习动机对数学问题提出能力有一定的影响。

从图3中可知，学生的学习习惯越好，其提出数学问题的能力越好。良好的学习习惯是促进学生数学问题提出能力提高的重要因素之一。因此，一线教师应培养学生课前预习、课后复习、及时完成作业和反思的良好学习习惯。

第五，学习信念与数学问题提出能力。从表12中可知，sig.=0.000<0.05，由此验证，学生的学习信念对数学问题提出能力有一定的影响。

从图4中可知，学生的学习信念越强，其数学问题提出能力越好。因此，教师不仅要使学生树立正确的学习信念，更要端正自己的信念，才能引导学生往更好的方向发展。

第六，学习焦虑与数学问题提出能力。从表13中可知，sig.=0.000<0.05。由此验证，学生的学习焦虑对数学问题提出能力有一定的影响。

已有研究表明，适当的焦虑有利于学生学习，学生的数学焦虑既不能太高又不能完全没有，应处于一种理想状态^[10]。从图5中可知，学生的学习焦虑等级越高（学习焦虑所有题项是反向计分，若学生的学习焦虑得分越低，即等级越低，说明学生处于高焦虑状态），其数学问题提出能力越强。因此，在课堂教学过程中，消除学生过高的焦虑变得尤为重要。

第七，自我效能感与数学问题提出能力。从表14中可知，sig.=0.000<0.05。由此验证，学生的自我效能感对数学问题提出能力有一定的影响。

由图6可知，学生的自我效能感越强，其数学问题提出能力越强，但处于自我效能感中等水平及较低水平的学生其数学问题提出能力均呈现较弱状态。因此，教师应注重加强学生自我效能感的培养，以此提高学生的数学问题提出能力。

4 研究结论与建议

通过上述的数据分析可以得到以下结论：（1）都匀市初中学生的非智力因素处于中等以上水平;（2）都匀市初中学生的数学问题提出能力处于中等水平;（3）初中学生的非智力因素与数学问题提出能力之间呈显著正相关，其中相关性最强的是自我效能感、学习习惯和学习兴趣。下面从对学生数学问题提出能力影响最大的非智力因素入手，提出培养对策和建议，以期为一线教师进行数学问题提出能力的培养提供参考。

4.1 培养数学学习兴趣，提升学生数学问题提出能力

学习兴趣是推动学生求知的内在力量^[11]。由前述的分析结果可知，学生的学习兴趣与数学问题提出能力呈显著相关，培养学生的学习兴趣有利于提升学生的数学问题提出能力。下面主要从3个方面分析在课堂教学中如何培养学生的学习兴趣。

第一，激发学生提问的原生兴趣。原生兴趣来源于学生自身对知识本体的兴趣，是学生的认知基础及已有知识经验与将要学习的知识本体之间产生共鸣，从而激发学生学习新知的内在动力^[12]。根据原生兴趣的定义可知，要想激发学生提问的原生兴趣，就要使得学生在课堂开始时就对学习的知识产生兴趣。这就要求教师在备课时应思考如何设置恰当的教学情境触发学生记忆的开关，指引学生回忆相关知识，建立起新知与旧知之间的联系，引发学生思考，引导学生提出数学问题，提高学生的提问兴趣。

例如，在学习人教版数学教科书七年级上册“等式的性质”时，教师可在课堂开始之时板书本节内容标题，并询问学生“看到这个内容，你想知道什么？”“这个内容在小学的时候已经学过，为什么还要重新学习？”等问题，以此激发学生求知的原生兴趣。在此之后，教师便可通过年龄相等问题情境，设置数学问题，要求学生回答并仿造已有问题提出不同的数学问题。年龄情境最好附上相应的人物图片，可以是本班学生图片或是本班教师图片，通过图片的刺激及相关文字语言的叙述，唤起学生学习的欲望，激发学生的学习兴趣。

第二，创造学生提问的伴生兴趣。“伴生兴趣是指学生在教师的引导下，伴随着重难点的教学，在知识的解释、梳理、理解和应用中产生的兴趣。在该阶段学生的伴生兴趣主要来源于知识之间的内在联系、知识的性质和作用，等等。”^[13]因此，教师需挖掘教材与教材之间、知识与知识之间的内在关联，梳理知识网络，厘清知识之间的关系，做到心中有数，游刃有余。

例如，在学习人教版数学教科书七年级上册“解一元一次方程（合并同类项）”的过程中，教师可设置有趣的问题情境，吸引学生的眼球，让学生根据问题情境提出数学问题，并自主解决，在突破重难点的同时培养学生提出问题的能力。

第三，设置学生提问的衍生兴趣。衍生兴趣是指课堂教学结束之后，学生仍然保持想学习的兴趣。因为是课后兴趣，这就要求教师充分利用好课后探究，可以是阅读任务、难题解答，也可以是数学小实验、课后思考。

例如，在学习人教版数学教科书七年级上册“有理数的混合运算”结束之时，教师可设置一道有趣的数学小故事，比如：“有一个国王为了获得贫穷百姓的支持，决定施舍某个村庄中的每个男人1美元，每个女人0.4美元。为了不让自己花费过多，国王算来算去，想到一个巧妙的办法。决定在中午12点的时候施舍，因为他知道，在那个时候，村庄里有60%的男人都外出打猎去了，而外出打猎的都不用给钱。已知村庄里共有成年人口3 085人，儿童不计，女性比男性多。请问国王要施舍掉多少钱？”这个有趣的故事中并没有告诉村庄中到底有多少男性和女性，看起来是道怪题，实际上在这道题中国王要施舍的钱和男性的数量无关，也就是说无论村庄中的男性有多少，国王要施舍的钱是一样的。这道题可作为学生学习有理数的混合运算后的一道课后思考题，让学生自主发现这道怪题中的奥秘。

4.2 培养良好学习习惯，强化学生数学问题提出能力

学习习惯是在学习活动中规范自己学习的固定心理模式，学生只要能够建立起一个固定良好的心理模式，就能高效地学习。根据数据分析结果可知，学生的学习习惯对其数学问题提出能力有着较大的影响。培养良好的学习习惯是培养学生提出问题的基础，良好学习习惯包括反思质疑习惯，而反思质疑恰好是学生提问的来源，学生有了疑问就意味着学生有了问题。因此，学生在学习数学知识的过程中，教师应鼓励学生对学习内容进行反思，多问“为什么？”“是这样吗？”“还有没有其他方法？”“如果交换条件还会成立吗？”等。教师在面对学生的质疑时，应持有正确的态度，要做到允许学生的质疑，正视学生提出的问题。学生只有打破常有的思维定势，勇于质疑，善于反思，才有可能提出更多更好的问题。

4.3 树立正确的自我效能感，提高学生课堂参与

自我效能感是指学生对自己是否具备完成某项任务的自我判断，主要包括一般自我效能和学业自我效能。一般自我效能是指学生对待数学的态度，即对自己是否能够学好数学的能力判断;学业自我效能则是指在学习过程中，对待和处理数学问题的态度，也就是对自己能否成功发现问题、提出问题和解决问题的判断。自我效能感在学生学习过程中起着决定性作用，它不仅不同程度地影响着学生学习的兴趣、动机、习惯，还影响着学生的学习焦虑。特别是學业成绩处于劣势的学生，会更加认为自己无论如何也掌握不了数学中稍难的知识，久而久之便形成了一种恶性循环，只要遇到稍难点的知识或者问题，就会产生“不会做”“不懂”的心理暗示，随之便失去了克服困难的决心和学习的动力。同时，如若教师在课堂上鼓励学生提出问题，此类学生就会感到非常困难，并且会产生“只有学习好的人才能提出问题，我的学习不好，我提不出问题”的想法。为能更好地培养学生提出数学问题的能力，更多地培养创新型人才，以及提高学生的学业成绩，教师应注重学生自我效能感的发展，有针对性地、因材施教地关注学生，切实为学生着想，力求将每位暂时落后、对自己不自信的学生拉回到学习中。

课堂是师生交流互动的主要场所，自我效能感低下的学生大多不自信。因此，教师可在课堂活动中提高全体学生的参与度。课堂参与度的体现在学生对课堂问题的回答。为照顾不同水平的学生，教师要设置不同难度的问题。难度较大的题目让能力好的学生回答，能够充分激发学生的思考，不断提高学生的能力;难度较低的问题让能力较差的学生回答，不仅锻炼学生能力，还能增强学生的成就感。以求做到能力好的学生能创新，能力差点的学生能进步。

参考文献

[1]中华人民共和国教育部.义务教育数学课程标准（2011版）[M].北京：北京师范大学出版社，2012.

[2]中华人民共和国教育部.普通高中数学课程标准（2017版）[M].北京：人民教育出版社，2018：1.

[3]彭乃霞，向毅，姚惠.非智力因素对数学概括能力的影响研究——基于来自贵州少数民族地区的样本[J].数学通报，2015，54（5）：13-16+23.

[4]王光明，宋金锦，王兆云.高中生数学学习非智力特征调查问卷的编制[J].数学教育学报，2015，24（3）：17-27.

[5]彭乃霞，廖爽，吴现荣.贵州民族地区高中生数学焦虑成因调查分析与研究[J].数学通报，2010，49（5）：14-17+20.

[6]夏小刚，汪秉彝，吕传汉.中小学生提出数学问题能力的评价再探[J].数学教育学报，2008，17（2）：8-11.

[7]高岱亮，田春凤，陈云丽.评价学生提出问题能力的PTA量表初探[J].物理教师，2016，37（1）：2-4.

[8]徐斌艳，朱雁，鲍建生，等.我国八年级学生数学学科核心能力水平调查与分析[J].全球教育展望，2015，44（11）：57-67+120.

[9]杨晓明.SPSS在教育统计中的应用[M].北京：高等教育出版社，2012：178.

[10]彭乃霞，胡炜，胡云学.非智力因素对民族地区小学生数学学习成绩影响的调查与分析[J].黔南民族师范学院学报，2014，34（4）：69-72.

[11]张瑛，胡懿，邢焰，等.课堂教学“四点突破”教学理念的提出[J].黔南民族师范学院学报，2016，36（1）：74-77.

[12]黄应碧.“四点突破”教学范式兴趣创新的认识研究[D].都匀：黔南民族师范学院，2019.

[13]张宗娟.“四点突破”教学范式“激趣、培志、养成”功能的理论研究[D].都匀：黔南民族师范学院，2019.

Study on influence of non-intelligence factors on students′ ability of mathematical question-posing in junior middle school：take Duyun City as an example

XIANG Xing^1，2，PENG Nai-xia¹，MA Wei^1，2

（1.School of Mathematics and Statistics，Qiannan Normal University for Nationalities，Duyun，Guizhou558000，China;2.Tongren University Attached Middle School，Tongren，GuiZhou 554300，China）

Abstract The ability of mathematical problem-posing is one of the necessary abilities that students need to acquire，and non-intelligence factors have a great influence on it.Taking the seventh and eighth grade students in Duyun City as the research object，this thesis uses the questionnaire method to comprehend the general situation of non-intelligence factors and mathematical problem-solving ability of the middle school students in Duyun City，and explores the influence of non-intelligence factors of middle school students in Duyun City on mathematical problem-posing ability.The results show that  non-intelligence factors of the middle school students in Duyun City are above the average level，and the ability to propose mathematical problems is at the medium level. Students′ non-intelligence factors and other dimensions have a significant positive correlation with the ability to propose mathematical problems，among which learning interest，learning habit and self-efficacy have the greatest influence on the ability to propose mathematical problems.Therefore，teachers should cultivate student′s interest in mathematics learning，good learning habits，correct sense of self-efficacy and improve students′participation in class in order to cultivatetheir ability to propose mathematical problems in the teaching process.

Keywords non-intellectual factors; ability to raise mathematical questions; correlation analysis

[責任编辑 马晓宁]