稀土元素La掺杂对AlN性能影响的第一性原理研究

贾晓凤， 刘玉慧， 王 赫

(安阳工学院 机械工程学院， 安阳 455000)

1 引 言

纤锌矿构型的氮化铝(AlN)是目前常用的压电材料，在通讯设备中有广泛的应用，例如用于制备薄膜体声波谐振器(FBARs)以及固态装配谐振器(SMRs)等[1-3]. 此外，AlN具有非常高的居里温度(1423 K)，使其在高温下也可具有一定的压电性能[4]. 通常情况下，高居里温度材料的压电系数较低，较低的压电常数d33(5.5 pC/N)是制约AlN应用的最主要因素之一[5]. 因此，如何提升AlN的压电性能具有十分重要的研究意义和应用价值. 近年来，国内外有大量的学者通过掺杂合金元素对AlN的压电性能进行了改进. Yoshiki等[6]研究了一系列的二元合金元素组合共掺杂对AlN压电性能的影响，发现掺杂等量的Mg2+/Hf4+或者Mg2+/Zr4+时，体系具有非常出色的化学稳定性以及压电性能. Hiroyoshi等[7]研究了不同含量的Sc对AlN压电性能的影响，计算结果表明当Sc从0到0.75变化时，e33逐渐增大，C33逐渐降低，因此d33会随着Sc含量的增加会有大幅度的提升. 但对La掺杂AlN的电子结构、力学性能及压电性能的理论计算尚未见报道. 由于稀土元素La与Sc属于同族元素，且相对于Sc来说，La的原子半径更大、电负性更低，掺杂La对其压电性能的提升预期会更大. 因此本文采用基于密度泛函理论的第一性原理计算方法研究了稀土元素La掺杂对AlN力学性能、压电性能的影响，并对电子结构进行分析，揭示具体的作用机理.

2 计算方法

本文采用基于密度泛函理论的第一性原理计算程序VASP(Vienna Ab initio Simulation Package code)进行计算[8]. 交换关联泛函采用的是广义梯度近似框架下的PBE赝势[9]. 布里渊区中采用Monkhorst-Pack方法[10]划分网格，k点网格大小为5×5×2，截断半径为520 eV，电子自洽迭代的收敛标准为10-7eV，结构优化的收敛标准为体系中所有原子受力均小于0.01 eV/Å. 采用有限差分的方法计算了各体系的弹性常数矩阵，在此基础上进一步计算了一系列的力学性质. 压电应力张量矩阵通过密度泛函微扰理论进行计算[11, 12]. 最后，采用Lobster程序[13]对体系的化学键进行计算分析.

3 计算结果与分析

3.1 晶体结构优化

纤锌矿结构的AlN空间群为P63mc(No.186)，其中Al原子位置为2b (1/3, 2/3, 0.38)，N原子的位置为2b (1/3, 2/3, 0)，晶体结构模型如图1(a)所示. 为了研究La掺杂对AlN性能的影响，构建了2×2×2的AlN超胞，置换其中的一个Al原子为La原子，掺杂后体系的化学式为Al15La1N16，掺杂模型的原子结构示意图如图1(b)所示.

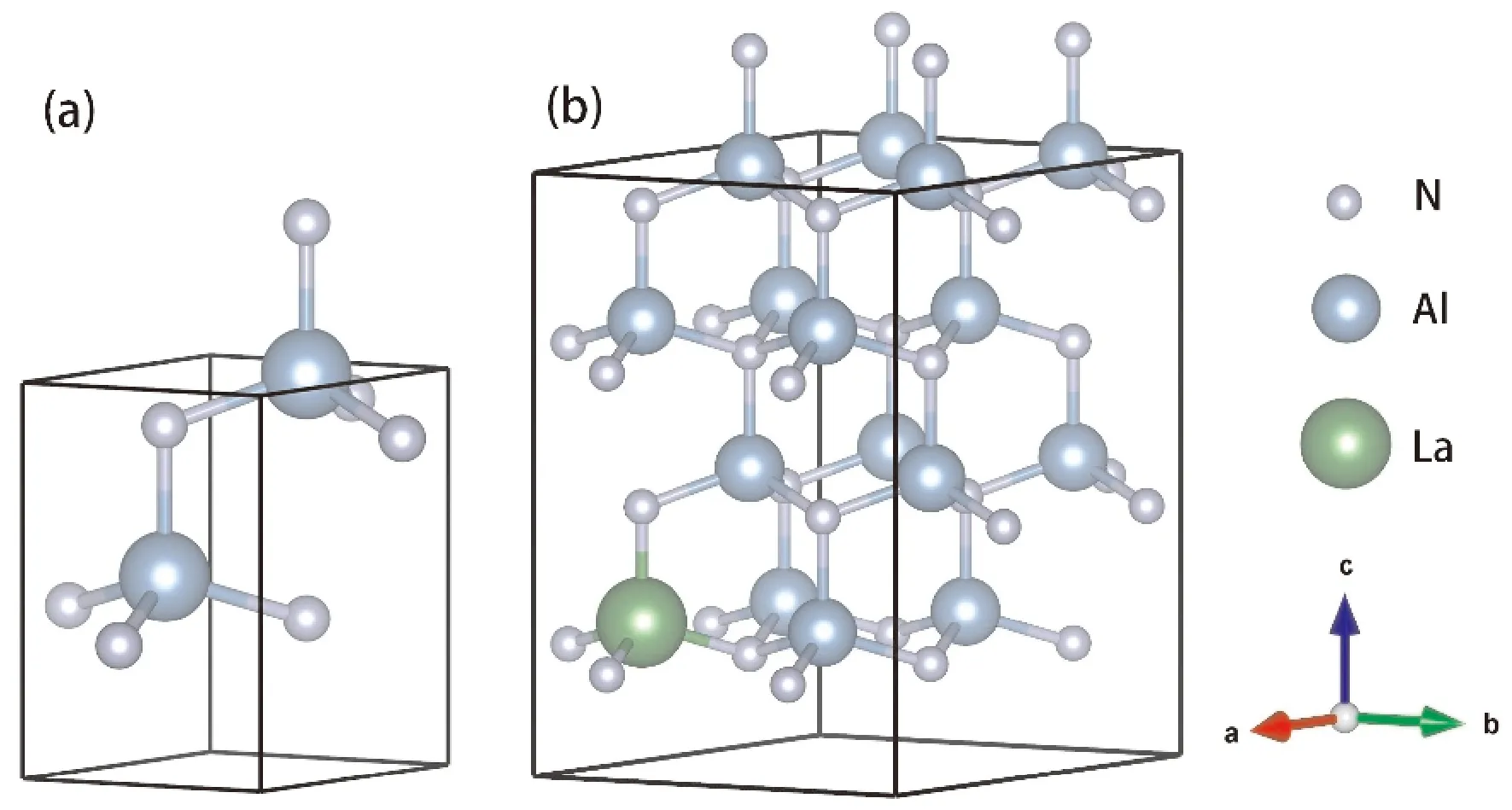
图1 (a) AlN的晶体结构模型 (b) Al15La1N16的超晶胞结构模型Fig. 1 (a) Crystal structure model of AlN (b) Crystal structure model of Al15La1N16

由于第一性原理计算是在0 K下进行的，0 K下的晶格常数与实验值有一定的差别，因此在进行第一性原理计算时首先要对晶体结构进行优化，得到最稳定的基态结构，在此基础上才可进行后续性质的计算. 计算得到的晶格参数列于表1中，计算结果与实验值[14]非常接近，这表明所选取的计算参数是十分可靠的，理论值略大于实验值是GGA近似的固有特征. 掺杂一个La原子后，体系仍保持原有的空间构型，a和b方向上的晶格矢量有略微的增大，这是因为La原子半径比Al原子半径大，而体系的c/a基本不发生改变.

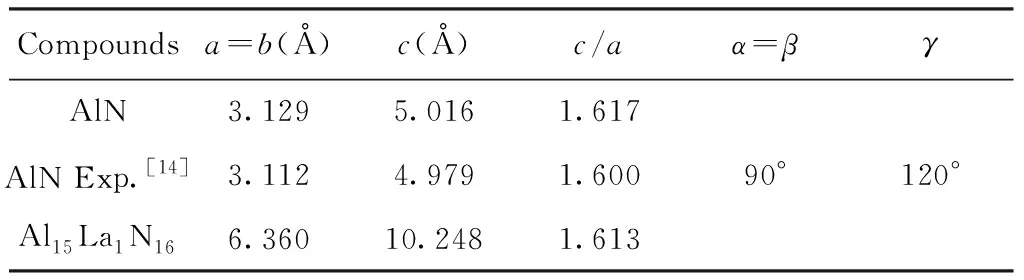
表1 纤锌矿结构AlN和Al15La1N16晶格常数

3.2 力学性质计算

材料的力学性质是评估其服役行为的一项重要指标. 通过实验测试各项力学性质成本太高，且耗时耗力，而采用第一性原理计算可方便、精确地计算出体系的各项力学性质. 首先采用有限差分法计算了各体系的弹性常数矩阵，由于晶体具有一定的对称性，弹性常数矩阵中的不同元素之间并不是完全独立的，计算得到的独立弹性常数结果如表2所示.

根据独立弹性常数首先可对体系的稳定性进行判定，AlN的空间群为P63mc，独立的弹性常数有五个：C11、C12、C13、C33、C44，其稳定性判据为：(i)C11> |C12|；(ii)2C132 0. Al15La1N16的空间群为P3m1，其独立弹性常数相比AlN增加了C14，其稳定性判据为：(i)C11- C12> 0 ；(ii)C132< 0.5C33(C11+C12) ；(iii)C142< 0.5C44(C11-C12) ；(iv)C44> 0[15,16]. 经验证，AlN与Al15La1N16均满足上述判据，表明这两种结构在力学上都是稳定的.

表2 计算得到的AlN和 Al15La1N16独立弹性常数

此外，通过独立弹性常数，根据V-R-H近似及相关理论，可进一步得到体模量B、剪切模量G、杨氏模量E、泊松比v等各项力学性质，相关结果列于表3中. AlN各项力学性质的计算值与实验值[17]十分接近，这表明本文的计算结果是十分可靠的. 掺杂La以后，体模量B、剪切模量G以及杨氏模量E均有一定程度的降低，意味着体系的强度有所降低. 材料韧脆性可由泊松比v、体模量与剪切模量之比B/G以及Cauchy压力C12-C44表征，当v> 0.26，B/G> 1.75，C12-C44> 0时，材料呈韧性，且其值越大韧性越好；反之材料呈脆性. 由计算结果可知，AlN为脆性材料，而掺杂La以后，体系呈韧性.

表3 计算得到AlN和 Al15La1N16的力学性能参数

3.3 压电性能计算

材料的压电性能是指在外力作用下，材料产生极化电荷的能力，是一种机械能向电能的转变过程，衡量AlN压电性能好坏的指标为压电常数d33. 在VASP中可以根据密度泛函微扰理论计算出压电张量矩阵得到e33，再由d33=e33/C33便可得到压电常数d33. 体系的压电效应由两部分贡献：一是晶格振动对外加力的响应所产生的极化，二是体系中电子对外加力的响应所产生的极化，两者之和便是总的压电张量矩阵. 相应的计算结果列于表4中. 可以看出，计算得到AlN的d33与实验值4.5～6.4 pC/N[18]非常接近，两者间的误差是由样品中所含的晶体缺陷造成的，这再次验证了本文计算的可靠性. 掺杂La以后，离子压电常数与电子压电常数都有一定的增大，但两者方向相反，总的e33略微升高，但掺杂后体系的C33有明显的降低，d33相对于AlN提升了15%左右.

表4 计算得到AlN和 Al15La1N16的压电性能指标

3.4 电子结构分析

上文计算结果表明，掺杂La以后体系的强度降低，韧性和压电性能均有一定的提升. 为了解释具体的作用机理，本小节对掺杂La前后体系的电子结构进行了分析.

图2为体系掺杂La前后的能带图，由计算结果可知，AlN的导带底和价带顶都在Γ点处取得，是一种直接带隙半导体，带隙大小为4.06 eV. 掺杂La以后，体系能带的展宽明显降低，这表明轨道间的作用强度变弱，即体系中原子间的化学键强度有一定程度的降低，从而降低了弹性常数. 此外，导带的能级明显地向低能级移动，导带底仍然位于Γ点，而价带顶位于K点，是一种带隙为2.44 eV的间接带隙半导体.

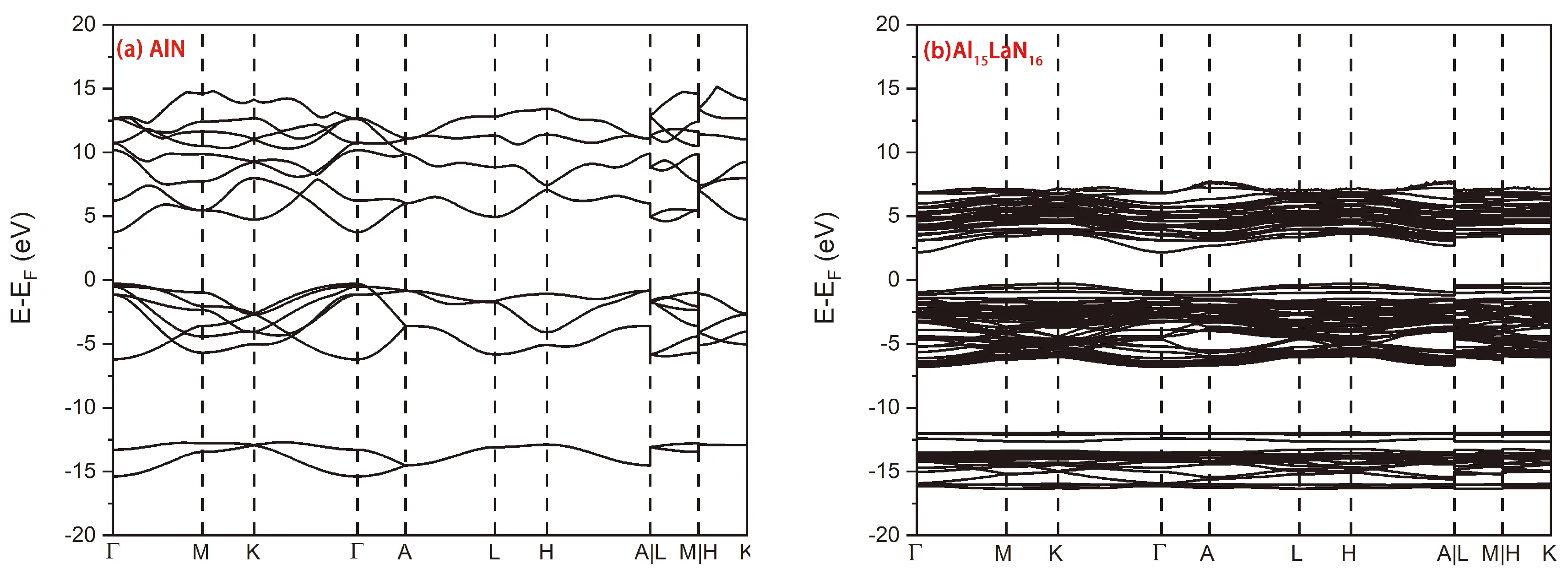
图2 (a) AlN的能带结构, (b) Al15La1N16的能带结构Fig. 2 (a) Band structure of AlN, (b) Band structure of Al15La1N16

图3为体系掺杂La前后的电子态密度. 从图3(a)可以看出，AlN电子的占据态主要集中在两个能级区间内：在-15 ～ -12.5 eV范围内的电子态由Al的s、p轨道以及N的s轨道贡献，且N的s轨道和Al的p轨道发生明显的杂化作用，产生Al-N共价键；从-6 eV到费米能级处的电子态由Al的s、p轨道以及N的p轨道贡献，同样地Al的p轨道与N的p轨道通过杂化作用生成Al-N共价键，这种强的共价键使体系非常稳定，难以进行弹性变形. 从图3(b)可以看出，掺杂La以后Al和N之间仍然存在强的杂化作用，此外La与Al和N只有在较深能级处才有强的杂化作用，而在费米能级附近，由于La的态密度非常小，产生的杂化效应十分有限，这意味着掺杂La会降低体系的强度，使得弹性常数有一定程度的降低.

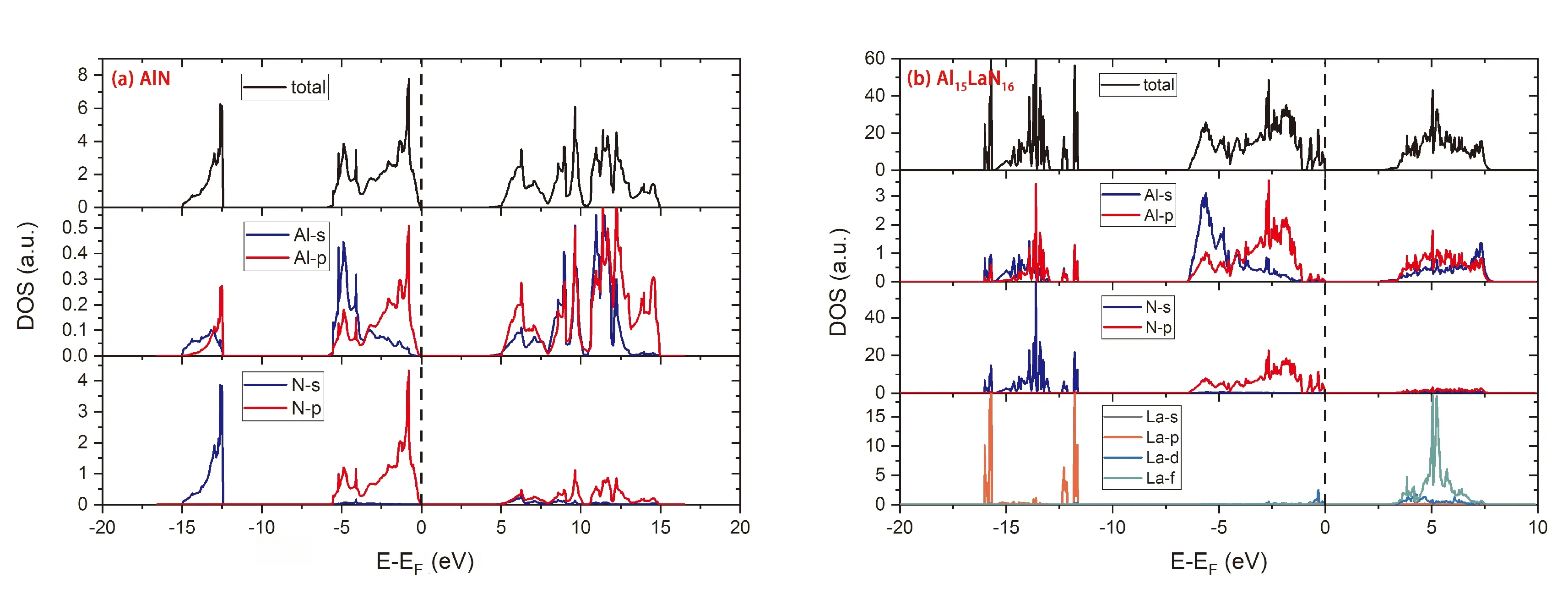
图3 (a)AlN的电子态密度, (b) Al15La1N16的电子态密度Fig.3 (a)Density of state of AlN, (b) Density of state of Al15La1N16

材料的强度、韧性与压电性能均与材料中化学键的强度相关，键强越大，材料的强度就越高，韧性就越差，在e33变化不大的情况下d33就越小. 在第一性原理计算中可通过晶体轨道哈密顿布局(COHP)分析成键态、反键态的贡献，进而定量地评估化学键的强度. 计算得到的晶体轨道哈密顿布局如图4所示. 图4(a)为AlN中Al-N键的COHP，负值代表成键态，正值代表反键态，可以看出，费米能级以下的电子态均为成键态，表明该化学键强度非常高，体系非常稳定. 图4(b)为掺杂La后体系中Al-N的COHP，可以看出在费米能级下方区域仍无反键态存在，但峰的强度有明显的降低. 图4(c)为掺杂La后体系中La-N键的COHP，可以明显的看出在费米能级以下存在反键态，对体系的稳定性有不利的贡献. 为了定量的评估化学键的强度，可对费米能级以下所有占据电子态的COHP进行积分，所得的积分值ICOHP即可定量地反映化学键作用的强度，即ICOHP的值越负，对应的化学键越稳定. 根据ICOHP的结果可知，掺杂La以后体系的Al-N键和La-N键的强度均比未掺杂的Al-N键低，表面掺杂La会降低体系的化学键强度，从而降低强度、增大韧性与压电性能.

图4 (a) AlN中Al-N键的COHP, (b) 掺杂La后Al-N键的COHP, (c)掺杂La后La-N键的COHPFig.4 Hamiltonian populations of the crystal orbitals of the bonds in AlN and Al15La1N16 for (a) Al-N bond, (b) La-doped Al-N bond, and (c) La-doped La-N bond

4 结 论

本文通过第一性原理计算从理论上预测了稀土元素掺杂对AlN性能的影响，得到的主要结论如下：

1)添加稀土元素La会降低体模量、剪切模量和杨氏模量.

2)添加稀土元素La会增大泊松比、B/G和Cauchy压力，使得AlN由脆性转变为韧性.

3)添加稀土元素La会使AlN的带隙减小，从直接带隙半导体变为间接带隙半导体，并使得体系的轨道作用强度变低.

4)添加稀土元素La会增大体系的压电常数d33.

5)添加稀土元素La会使得化学键的ICOHP升高，即降低化学键的强度，从而使得韧性增加，压电性能得到提升.