内地核中碳含量的第一性原理研究

陈 星， 刘 勋， 黄海军

( 武汉理工大学 理学院 高压物理和新材料研究中心 武汉 430070 )

1 引 言

地球形成过程会在地核及地幔中留下地球物理和地球化学方面的痕迹. 地震波观测表明，地核是由铁及少量轻元素组成. 确定地核中轻元素的种类和含量有助于构建早期地球形成的模型，解释地球物理现象以及预测地球未来的发展[1-5]. 由于碳元素在核-幔分离条件下对液态铁具有高亲和性，并且在太阳系和C1碳质球粒陨石中含量较高，被认为是地核中重要的轻元素之一[6, 7]. 地球内核具有异常高的泊松比，在众多候选轻元素(碳，氢，氧，硫和硅)中，只有铁碳化合物的泊松比接近内地核[8, 9]. 因此，碳可能是内地核中主要的轻元素，甚至一些研究表明内地核几乎完全是由铁碳化合物组成[9]. 通常认为内地核中铁碳化合物的存在形式是Fe3C和Fe7C3，目前这两种铁碳化合物都已得到广泛的研究[6, 10-16]. 虽然大部分研究认为在内地核条件下Fe7C3比Fe3C更稳定，但在最新的研究中Takahashi等人通过实验发现Fe3C在内地核条件下可以稳定存在[17].

约束内地核中碳含量最直接的方法是在地核条件下测量铁碳化合物的密度和声速，并将其与地震波模型(如初始地球参考模型-PREM)进行比较. 在内地核条件(330-360 GPa，5000-7000 K)下直接测量物质的性质仍然非常困难. 目前对Fe3C状态方程和声速的测量局限于相对较低的压力和温度条件. 实验测量的Fe3C声速数据即使在室温高压条件下也显示出很大的差异，将这些结果外推至内地核条件会带来很大的不确定性. 另一方面，基于第一性原理的模拟计算没有上述限制. 本文通过第一性原理GGA-PBE方法计算了0-K下Fe3C的状态方程和声速，并将这些结果外推至内地核温度条件，通过与PREM模型比较以限定内地核中的碳含量.

2 计算方法

常态下，Fe3C为正交结构(图1)，空间群为Pnma，其晶格常数为a=5.077 Å，b=6.724 Å以及c=4.515 Å[18]. 本文采取GGA-PBE方法进行赝势平面波计算[19]，计算选取的截断能为500 eV，Monkhorst-Pack网格为6×4×7，几何优化算法为BFGS[21]，采用超软赝势来描述离子-电子间的相互作用[20]. 模拟晶胞包含12个Fe原子和4个C原子，计算包含Fe 3d64s2和C 2s22p2电子. Fe3C在高压下经历了从铁磁性相(FM)到非磁性相(NM)的同构型转变，文献中报道的相变压力还存在争议(4.3-55 GPa). 为了研究Fe3C在高压下的磁性相变，我们对其进行了自旋限制和自旋非限制计算. 根据胡克定律计算了非磁性相Fe3C的弹性常数并进而得到其声速. 我们也对不同压力下的电子态密度进行了计算以获得其对热压的贡献.

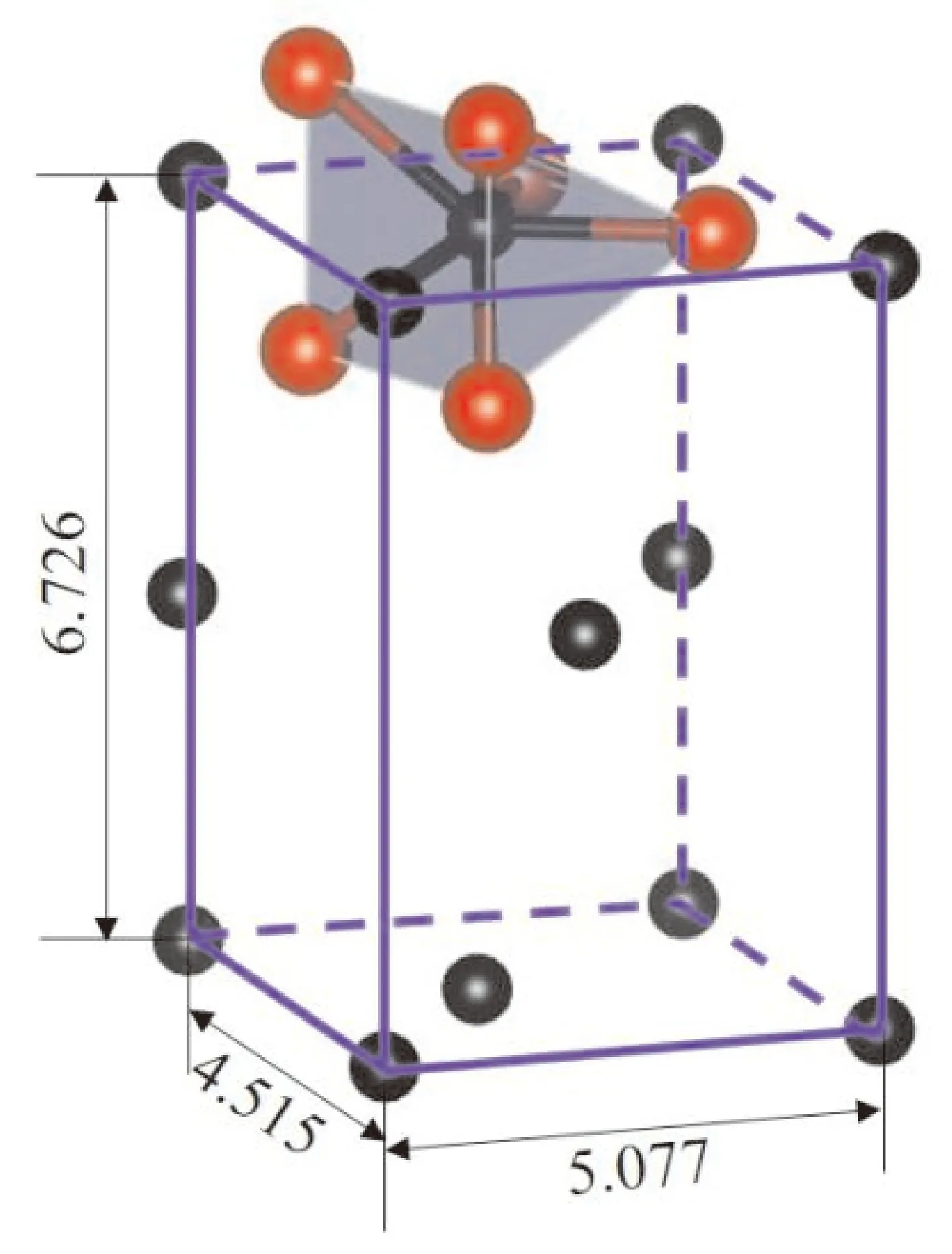
图1 Fe3C在常态下的晶体结构. 黑色和红色的球分别代表C和Fe原子，每个C原子被六个Fe原子包围形成一个八面体，此处仅显示一个八面体. Fig. 1 Crystal structure of Fe3C at ambient conditions. Black and red balls represent C and Fe atoms, respectively. Avery C atom is surrounded by six Fe atoms to form an octahedron, only one octahedron is shown here.

3 计算结果

图2显示了有和没有自旋限制的情况下，计算所得Fe3C的0-K等温线. 结果显示没有自旋限制的等温线在40 GPa处出现不连续，表明存在相变，相变处的密度增加了约2%，压力超过40 GPa后，这两者趋于一致. 计算的 Fe3C随压力变化的磁矩绘制在图3中，当压力小于40 GPa时，磁矩随着压力的增加而缓慢减小，当压力大于40 GPa时，磁矩突然下降至接近0，表明在40 GPa时Fe3C由铁磁相转变为非磁性相. 在静高压实验中，Fe3C的自旋相变已获得广泛的研究. 使用X射线发射谱，Lin等人报道Fe3C在25 GPa存在磁坍塌[22]. 基于同步辐射穆斯保尔谱测量，Gao等人报道Fe3C在4.3-6.5 GPa出现磁性相变[23]. 根据X射线磁圆二色性测量，Acet等人报道Fe3C在9 GPa附近存在磁性转变[24]. Ono等人通过X射线衍射技术测量了0-70 GPa压力范围内Fe3C的状态方程，他们发现在55 GPa处存在1.7%的体积塌缩并将其解释为磁性相变[25]. 最近，Chen等人通过X射线发射谱重新检测了Fe3C在高压下的磁性性质，他们的研究结果表明Fe3C在10-50 GPa之间会逐步发生铁磁性到顺磁性，再到非磁性的转变[8]，我们的计算结果与这个结论吻合. 计算得到的0-K等温线与静高压实验获得的300-K等温线数据也基本一致[16, 25-28]. 对铁磁性和非磁性相，使用三阶Birch-Murnaghan状态方程对计算结果进行拟合可得K0= 235 GPa，K0′= 4.0(铁磁相)和K0= 332 GPa，K0′= 4.6 (非磁性相)，其中K0为体积模量，K0′ 为其压力偏导数. 在表I中，我们将拟合获得的状态方程参数与实验结果进行了比较，对于铁磁性相，计算的体积模量略高于实验结果. 对于非磁性相，所得结果与Takahashi等人的最新结果非常吻合[17].

图2 Fe3C的静态等温线具有(蓝色实心圆)和没有(红色实心圆)自旋限制Fig. 2 Static isothermals of Fe3C calculated with (blue solid circles) and without (red solid circles) spin restriction

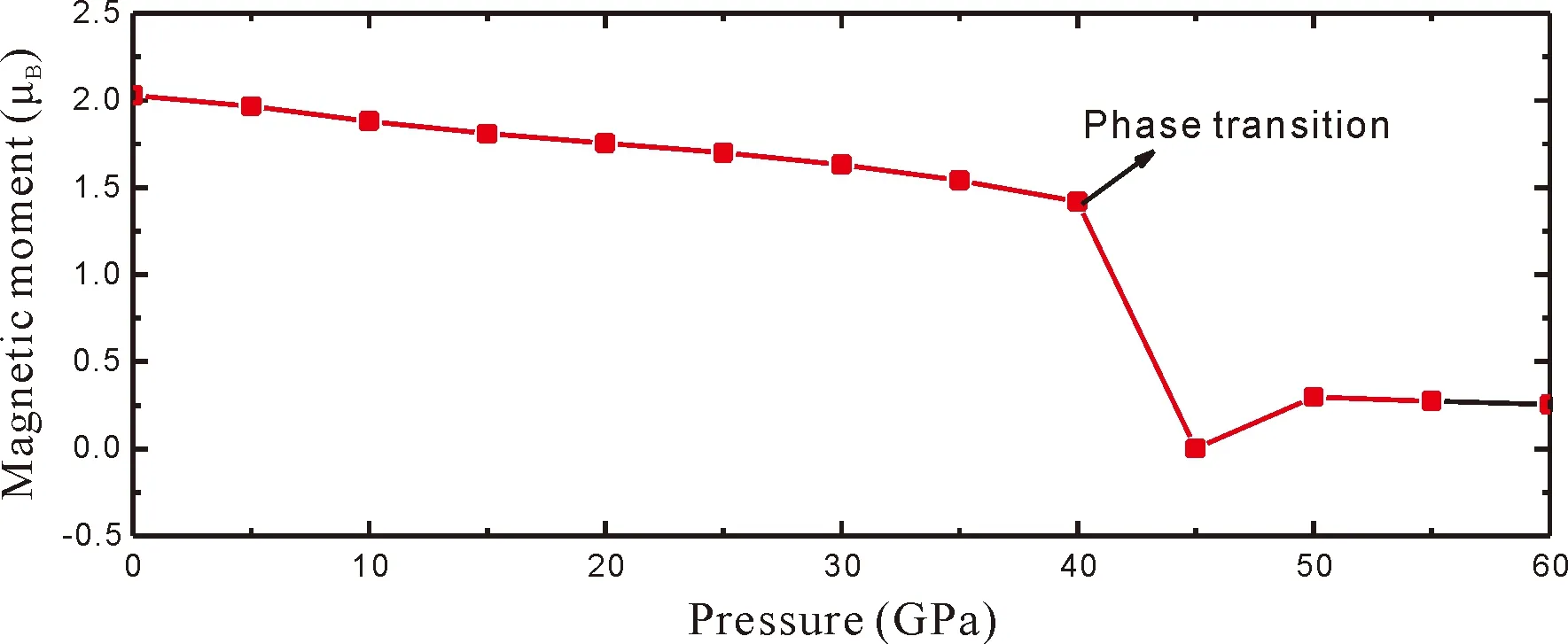
图3 高压下Fe3C的磁矩Fig. 3 Magnetic moments of Fe3C at high pressure

计算所得的弹性常数如图4(a)所示. 因为我们关注的是Fe3C在内地核压力下的性质，因而只计算了非磁性相Fe3C的弹性常数. 所有的弹性常数都随压力升高而线性增大. 发生弹性应变的晶体只有在其内能增加的情况下才保持稳定. 对于正交晶体如Fe3C，该稳定性判据表现为[29]：

表1 Fe3C的状态方程参数

C22+C33-2C23>0,

(1)

C11+C22+C33+2C12+2C13+2C23>0,

(2)

C11>0,C22>0,C33>0,

C44>0,C55>0,C66>0.

(3)

计算所得的C44在零压下为负值，表明非磁性相Fe3C在零压下不稳定. 但随着压力的增加，非磁性相稳定性增加，C44也变为正值. (C22+C33- 2C23)为正值，并且随着压力升高而增加，如图4(b)所示，表明非磁性相Fe3C在内地核压力下保持机械稳定.

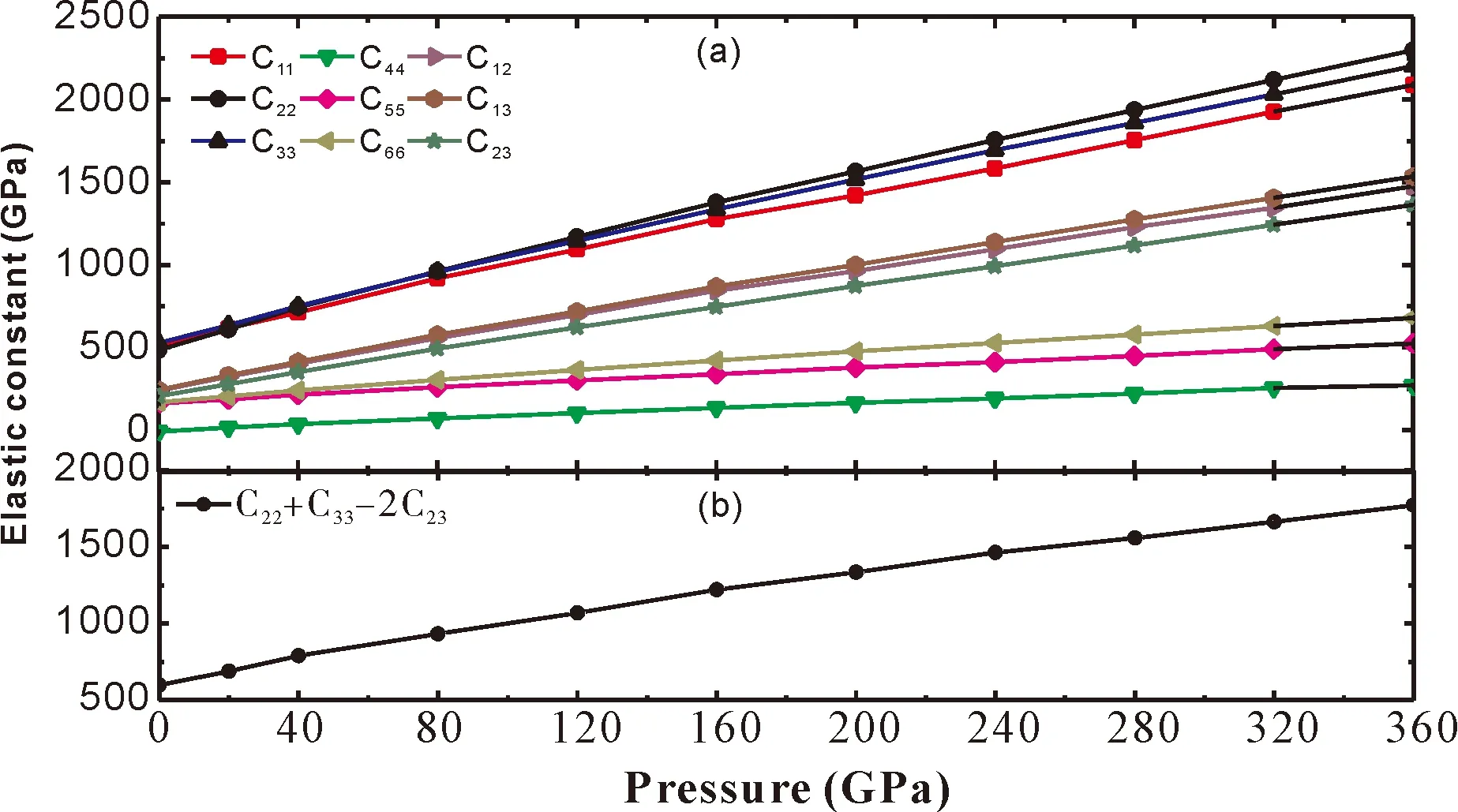
图4 (a)NM相Fe3C在高压下的弹性常数；(b)(C22 + C33-2C23)的值与压力的关系Fig. 4 (a) Elastic constants of NM phase Fe3C at high pressure; (b) The value of C22+C33-2C23 versus pressure

为了获得电子的热压贡献，我们在0 ～ 360 GPa压力范围内计算了非磁性相Fe3C的电子态密度，压力间隔为40 GPa，计算结果如图5(a)所示. 不同压力下的电子总态密度相似，费米能级处的电子态密度不为零，表明Fe3C在整个压力范围内为金属，因而其在极端条件下的电子热压贡献不可忽略. 图5(b)所示为P= 120 GPa时的部分电子态密度，可见主要贡献来自于铁的3d电子.

图5 (a)最高360 GPa，间隔为40 GPa的Fe3C的总电子态密度；(b)P = 120 GPa时的典型局部电子态密度，黑色虚线表示费米能级Fig. 5 (a) Total electronic DOSs of Fe3C up to 360 GPa with an interval of 40 GPa; (b) Typical partial DOS at P=120 GPa. Black dashed lines indicate Fermi level.

4 热力学计算和地球物理意义

地球内核处于高压高温状态，为了约束地核中的碳含量，必须将计算所得的0-K等温线外推至高温条件. 我们将热压写为：

(4)

其中V=1/r为比容，g为格林爱森参数. 晶格热容Cvib=3R/m，其中R为理想气体常数，m为摩尔质量. 电子热容Ce=β0(V/V0)γeT，其中b0为电子比热系数，ge为电子格林爱森参数[30]. 有效格林爱森参数可表述为[31]：

γ=(γvibCvib+γeCe)/CV,

(5)

其中gvib=gvib,0(V/V0)q为晶格对格林爱森参数的贡献，gvib,0是零压和零温下的晶格格林爱森参数，q为常数. 由上述表达式可以得到：

(6)

上式中有四个参数gvib,0，q，b0和ge需要确定. 一般需要通过计算声子谱来确定gvib，这里我们使用德拜格林爱森参数gD来代替，它与德拜声速vD的关系如下[32]：

(7)

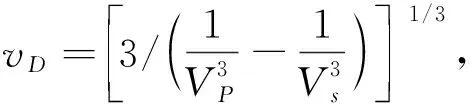
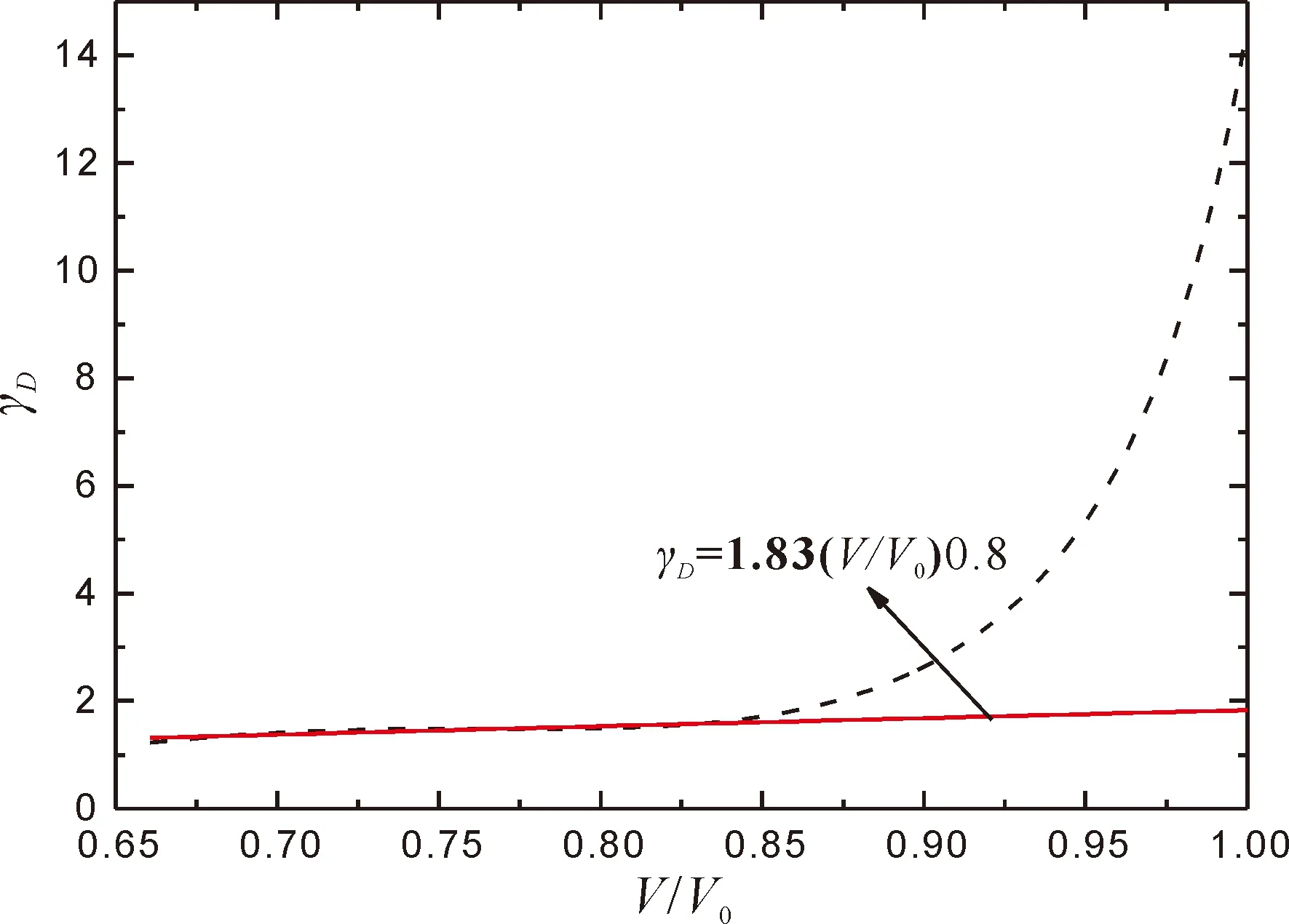
图6 计算所得高压下非磁性相Fe3C的德拜Grüneison参数gDFig.6 Calculated Debye Grüneison parameter gD of NM phase Fe3C at high pressure

电子格林爱森参数ge和比热系数b0可以通过计算出的电子态密度来确定. 电子内能为：

(8)

其中D(e) 为电子态密度，f(e) 为费米分布函数[34]. 如果电子态密度在费米能级附近没有快速变化，将Sommerfeld展开应用于(8)式，则可得电子比热为：

(9)

现根据(6)式和上面确定的热力学参数，将Fe3C的0-K等温线外推至内地核条件. 内地核的温度剖面由Tg=TICB(rI/rICB)1.5确定，其中rI是地核密度，TICB和rICB分别是内-外地核边界处的温度和密度. 根据Hirose的讨论，取TICB=5400 K，计算结果如图7所示，相同压力下Fe3C的密度比PREM值低约0.67 g/cm3[37]. 我们也根据Fei等人报道的状态方程参数计算了内地核条件下纯铁的密度[38]. 如果Fe和Fe3C为理想混合，计算结果表明需要47 wt%的Fe3C来解释内地核的密度亏损，这意味着如果碳是内核中唯一的轻元素且以Fe3C的形式存在，则内地核含有最多3.1wt%的碳. Murphy等人通过实验测量发现铁的gvib比gD大约10%，我们通过计算发现晶格格林爱森参数的微小变化不会影响上述讨论结果.

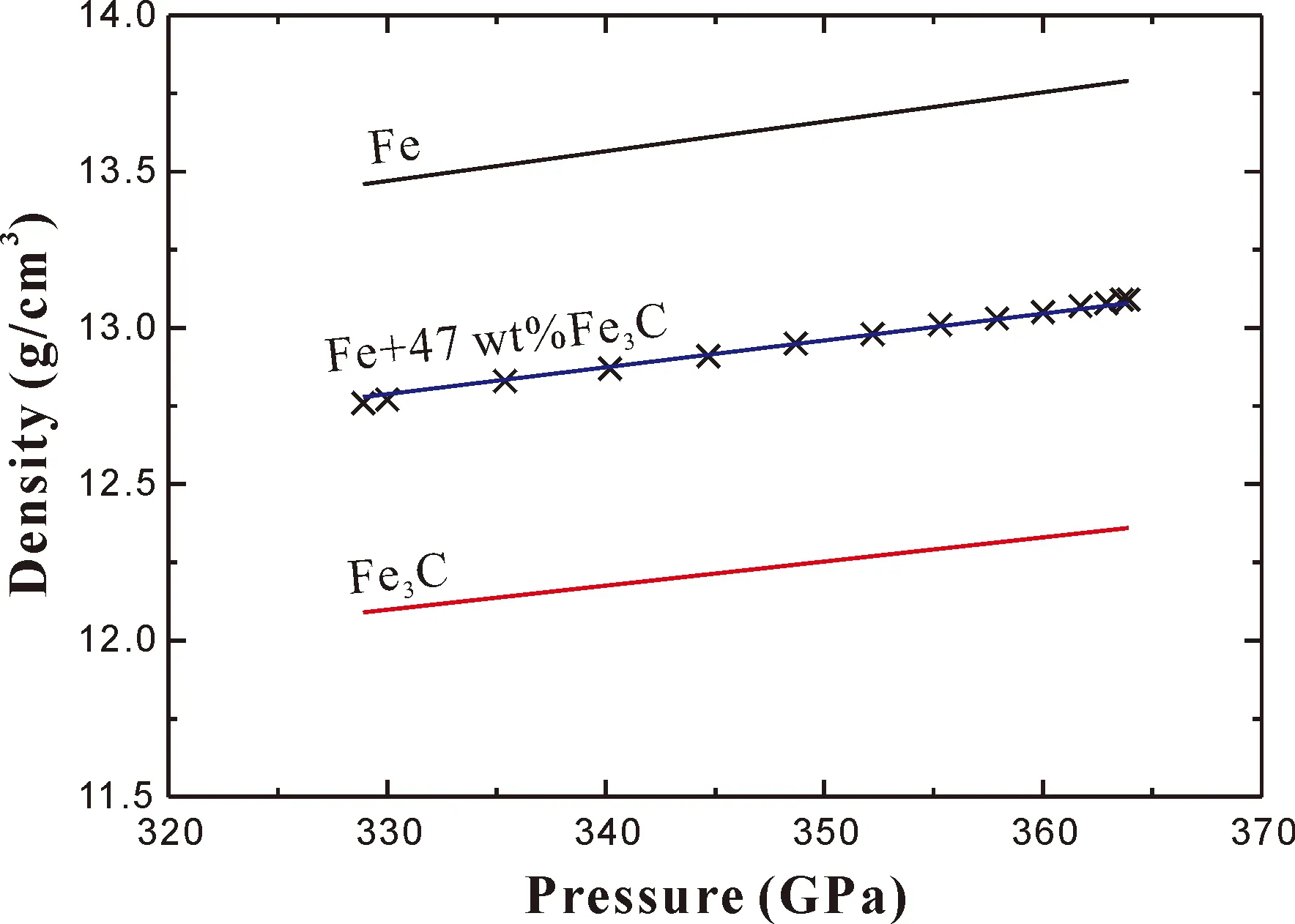
图7 内地核条件下Fe3C(红线)和纯铁(黑线)的密度. 蓝线为根据理想混合计算的Fe+47wt%Fe3C的密度，黑色十字为PREM模型. Fig.7 Densities of Fe3C (red line) and pure iron (black line) at the inner core conditions. The blue lines are sound velocities of pure iron and black crosses are from PREM.

地核中适当的轻元素应能够同时解释纯铁和地震波观测值之间的密度和声速差异. 实验测量的Fe3C在高压下的声速数据存在很大差异，如图8所示[8, 23, 39, 40]，将这些结果外推到内地核条件将得出截然不同的结论. 压力较低时，我们计算的结果与实验结果非常吻合，但是由于非磁性相Fe3C的不稳定性导致零压下的Vs明显较小. 在较高的压力下，Vp和Vs均高于Chen等人的实验结果[8]. 在内地核压力下，Fe3C的Vp高于纯铁，且Vs与纯铁相当[41]. 地核中的轻元素应降低纯铁的Vp和Vs使其更接近PREM值，碳因而不是一个好的选择. 从目前的研究结果看，温度对Fe3C声速的影响还尚未可知. Gao等人在低压下对Fe3C进行的实验测量表明温度对Vp的影响可忽略不计，但对Vs的影响较为明显，他们推断在内地核的温度条件下，Vs可能最多会下降30%[42]. 我们计算的Vs比PREM值高2.14 km / s，减小30%后仍然比PREM值高0.43 km / s，因此我们的计算结果表明碳不是内地核中主要的轻元素.

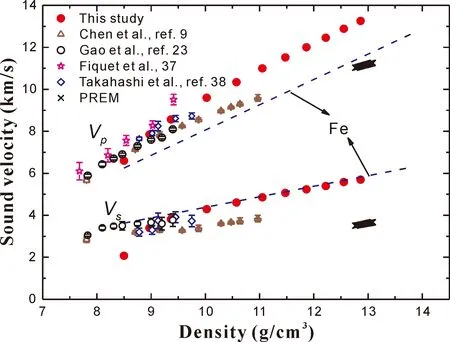
图8 计算得到的Fe3C声速与实验结果的比较(蓝线是纯铁的声速，黑色十字为PREM值)Fig.8 Comparison of the calculated Fe3C sound velocities with available experimental results (The blue lines are sound velocities of pure iron and black crosses are from PREM)

5 结 论

总结，我们通过第一性原理GGA-PBE方法计算了高压下Fe3C的热状态方程和声速. 计算结果表明Fe3C在40 GPa由铁磁性相转变为非磁性相. 将Fe3C的0-K等温线外推至内地核温压条件发现内地核中碳含量最多为3.1wt%. 另一方面，计算得出的Fe3C声速数据表明碳不应是内地核中主要的轻元素.