团簇的几何结构、电子和光谱特性
2021-09-16李文静李果磊周丽鸽王愿香刘珊珊李成刚崔颍琦任保增胡燕飞
李文静, 李果磊, 马 宇, 周丽鸽, 王愿香, 刘珊珊, 李成刚,, 崔颍琦, 任保增, 胡燕飞
(1. 郑州师范学院物理与电子工程学院量子材料研究中心, 郑州450044;2. 郑州大学化工与能源学院, 郑州 450001;3. 四川轻化工大学 物理与电子工程学院, 自贡 643000)
1 引 言
由于硼原子的缺电子特性(3个价电子),在很多情况下易形成多中心键,使得硼团簇易产生不同寻常的新颖结构和奇异物理化学特性[1-5].在过去的几十年里,硼团簇的结构及特性研究备受科学家的关注.研究发现,随着原子数的变化,硼团簇体系展现了多种几何结构,包括平面或准平面、管状、笼状、双层级核壳结构等.对于阴性硼团簇Bn-,n<38时的团簇具有平面或准平面结构[6-7].而中性的硼团簇中,不同大小的硼团簇具有平面、准平面、管状、笼式和其它三维结构[8-11].最近几年硼球烯(B40;borospherene)的发现是低维硼纳米材料和团簇科学的重要突破[12].特别是布朗大学Lai-Sheng Wang课题组与包括山西大学李思殿、翟金华教授、清华大学李隼教授课题组,基于理论和实践相互结合、互相印证的方式,揭示了中小尺寸硼纳米团簇的结构特征,为硼基纳米材料的研究指明了方向.
基于平面和准平面结构,科研工作者研究构建了大量稳定性高的硼基纳米材料,例如,Wankel马达和亚纳米坦克履带等单原子层的纳米机器等[13-16].但是,由于B原子的sp2杂化的缺失,在构建三维尺寸下的硼基纳米体系材料遇到很大的困难.研究发现,硼的缺电子性意味着其更容易受到金属原子的影响,进而有效提高三维硼基纳米材料的稳定性.广大科研工作者利用掺杂的方法先后寻找出一系列金属原子(过渡元素、碱金属元素和稀土元素)掺杂硼基纳米团簇结构,并对掺杂体系的结构和电子特性进行了广泛研究.特别是过渡金属掺杂硼团簇产生的高对称性管状结构引起了我们的注意.例如:基于密度泛函理论的第一性原理计算,Dong等人[17]预测了高对称性的最小管状(D6d)Li2B12团簇,其结构中两个Li原子位居B12管的上下方.通过实验的光电子能谱和第一性原理计算,Jian等人[18]报道了以Mn为中心的双环管状MnB16-团簇,其中Mn原子的3d轨道和B16管中B原子之间强烈的共价键作用提高了管状结构的稳定性.最近Li课题组[19]研究发现了三环管状结构的Ta2B17+,两个Ta原子靠近管的上下表面,而且,每个Ta中心都遵循18电子规则,该结构可以作为构建单壁金属硼纳米管的胚胎.此外,Popov[20]和Li[21]等课题组分别从实验确认了高配位的管状CoB16-和TaB20-团簇.特别是在我们前期工作中,对过渡金属掺杂MB16-(M=V, Cr, Mn, Fe, Co)的结构和电子特性进行了详细分析,结果发现,除了NiB16-(Cs)外,其它掺杂体系都呈现管状高对称性(C2v, C4v, C4v, D8d, D8d)的稳定结构[22].可以说管状的过渡金属掺杂硼基纳米材料在提高硼基纳米材料的稳定性方面发挥着重要的作用,极大丰富了人们对硼团簇的认识.在文献[22]中,我们曾以FeB16-和CoB16-为胚胎构建了Fe2B24-和Co2B24-团簇,优化结果发现了两个高对称的C4v点群对称结构,在此结构基础上,对其特性进行了系统研究.对于其它过渡金属原子体系的堆积,其结构又会呈现什么特征呢?如果在保持原子比不变的情况下,增大研究对象的尺寸,结构和特性会如何变化呢?据我们所知,目前还没有关于钒硼原子个数之比为某一定值的报道.因此,在密度泛函理论的计算框架下,我们对VnB8(n+1)-(n=1-3)团簇的几何结构、电子和光谱特性进行了系统研究,希望为设计新型过渡金属掺杂硼基纳米管材料提供理论参考.
2 计算方法
本文首先采用吉林大学马琰铭教授课题组研发的基于粒子群优化算法的卡里普索结构预测方法预测VB16-团簇的初始结构[23-25].该方法只根据材料的化学配(一定压力和温度条件下)就可合理预测其结构的理论技术,预测结果的合理性已经得到广泛验证[23-30].初始VB16-结构的预测过程如下:首先,利用PBE0泛函和3-21G基组预测出1000个结构.然后,采用PBE0泛函[31, 32]和6-311+G(d)全电子基组[33]对上述结构中能量差超过0.3 eV的结构进行优化.在优化过程中,通过频率分析考察了优化结构是否真实存在,所有的计算都在Gaussian 09[34]程序下运行.然后,基于预测优化出的VB16-结构通过堆积的方式,构建了V2B24-和V3B32-的结构,然后利用DMol3软件包对堆积结构进行优化[35-37].优化过程采用基于密度泛函理论的GGA方法[38],选择Perdew-Burke-Erznerhof(PBE)交换相关泛函,对团簇中的电子采用全电子计算,基组选用带极化的双数值原子基组DND.几何构型优化时最大梯度和最大位移收敛值均小于10-3a.u.,能量收敛值优于10-5a.u.,计算过程中体系的自旋不做限制.
3 结果讨论
3.1 VB16-,V2B24-和V3B32-团簇的基态结构
本节中,首先利用卡里普索结构预测方法和密度泛函理论的第一性原理计算,预测得到了VB16-基态结构为V原子位居中心的高对称(C2v)性管状结构(图1).在VB16-基态结构上通过堆积并利用DMOL3优化后的V2B24-和V3B32-团簇具有C4h和D8d的高点群对称性(图1).

图1 团簇基态结构、蓝色代表V原子,绿色代表B原子Fig. 1 The lowest energy structures of VnB8(n+1)-(n=1-3) clusters, along with the point group symmetry in brackets. The vanadium and boron atoms are shown as blue and green spheres, respectively.
3.2 HOMO-LUMO能隙
最高占据轨道(HOMO)和最低未轨道(LUMO)之间的能隙反映了电子从HOMO能级跃迁到LUMO能级的能力,其值越大,团簇分子的化学活泼性越低,对应的团簇化学稳定性越强.计算发现,VB16-,V2B24-和V3B32-团簇的HOMO-LUMO分别为:2.08 eV,1.59 eV和2.51 eV(图2).即,相对于VB16-和V2B24-,V3B32-团簇得失电子相对困难,化学性质更为稳定一些.
3.3 自然布局分布和自然电子组态
本文中,我们采用自然布局分布(natural population analysis,NPA)和自然电子组态(natural electron configuration,NEC)方法对体系的电荷性质进行了研究.结果发现,对于VB16-,中间的V原子拥有1.270 e电荷;对于V2B24-,中间的两个V原子分别拥有2.143 e电荷;对于V3B32-,中间3个V分别拥有2.023 e、1.972 e和5.362 e电荷.上述数据充分说明,电荷从钒向硼原子转移,该特征符合V原子(1.63 eV)比B原子(2.04 eV)拥有相对小的电负性[39].为了确保NPA电荷计算结果的准确性,基于Multiwfn软件[40],采用了巴德电荷分析(Bader charge analysis)方法对电荷分析进行了分析.结果显示,不同尺寸下V原子周围的电荷分别为:1.266 e;0.826 e和0.826 e;1.164 e、0.764 e和1.166 e.数据也说明,电荷从钒向硼原子转移.虽然两种方法下转移的电荷值不同,但是,对于电荷分布的计算,电荷的绝对值是没有意义的,其数值受到所用方法和基组的影响.此外,自由B原子的电子排布为2s22p1,自由V原子的电子排布为[Ar]3p63d34s2.当形成团簇后,B的自然电子组态为:2s0.67-0.732p2.17-2.353p0.01-0.02;2s0.51-0.672p1.54-2.403p0.02-0.03;2s0.44-0.682p2.29-2.613p0.02-0.03,V的自然电子组态为:3d3.944s0.024d0.31;3d4.20-4.214s0.214d0.46-0.47;3d3.63-4.244s0.03-0.224d0.32-1.61.说明B-2s失去电子,B-2p得到电子;V-3d得到电子,V-4s失去电子.这意味着,电子从B-2s和V-4s向V-3d和B-2p轨道转移,钒和硼原子之间存在强烈的spd轨道杂化.
3.4 电子局域密度函数和Mayer键级
为了更深入了解原子间的关系,本节中,计算了VB16-,V2B24-和V3B32-团簇的电子局域密度函数 (electron localization function,ELF),该方法不仅可以定量的表示电子在空间分布的局域化程度和局域化特征,对多电子系统中电子对的分布概率给出直观的显示,还可以用于辅助分析成键类型.一般来说,ELF的取值在[0, 1]区间,值为1表示电子的完全局域化,值为0意味着此处没有电子或者电子完全离域化.图3中,对于VB16-,V2B24-和V3B32-团簇中管状结构的不同截面进行了电子定域函数的计算.对比不同原子间的填色图发现,VB16-中上下两个表面中B-B之间的共价键比V2B24-和V3B32-团簇中B-B之间共价键强.为了验证分析的合理性,我们利用Mayer键级分析了上述截面中的B-B的键级,结果发现,VB16-中上下两个截面中B-B的Mayer键级都是0.911,V-B的Mayer键级的平均值为0.524;V2B24-中,上、下两个截面中B-B的Mayer键级分别为0.861和0.861,而V-B的Mayer键级的平均值为0.559;V3B32-中上下两个截面的B-B的Mayer键级分别为0.886、和0.886,V-B的Mayer键级的平均值为0.481.上述数据表明,VB16-团簇中B-B之间的共价键最强,V3B32-团簇中V-B之间的离子键最弱.

图 3 VB16-,V2B24-和V3B32-团簇基态结构中不同截面的电子局域函数Fig. 3 The electron localization functions from different sections of the lowest energy structure of VB16-, V2B24- and V3B32- clusters.
3.5 红外和拉曼光谱
基于研究对象的基态结构,本节中利用Multiwfn软件拟合出了VB16-,V2B24-和V3B32-团簇的红外和拉曼光谱,横坐标(cm-1)代表振动频率,纵坐标分别代表红外光谱强度和拉曼光谱的活性,单位分别对应于km/mol和Å4·amu-1.从图4发现,三种不同尺寸团簇的红外和拉曼谱峰主要集中在200~1000 cm-1范围内,对于红外谱,不同尺寸团簇对应的最强峰分别位于461 cm-1,442 cm-1和606 cm-1处,其中,VB16-表现为中心V原子随着4B,5B,6B和7B原子所在平面的左右摇摆振动模式;V2B24-表现为上下两个面内B原子的左右摇摆振动模式,进而带动两个V和中间的B原子的受迫振动.V3B32-表现为中间V原子上下往复振动和中间两层B原子的呼吸振动模式.而且,最强峰对应的频率可以作为团簇的IR测量指纹.对于拉曼谱,VB16-,V2B24-和V3B32-对应的最强峰分别位于714 cm-1,632 cm-1和662 cm-1处.VB16-表现为上面两个平面内的B原子绕V原子呼吸振动模式,而中心的V原子几乎不动;V2B24-表现三个面内所有B原子,以两个V原子为中心的呼吸振动模式,类似于VB16-的振动模式,中心的两个V原子几乎静止不动;V3B32-表现为中间V原子静止不动,上面两层B原子呼吸振动,而中间两层B原子上下振动的模式.上述的最强峰可用来表征不同尺寸团簇的管状结构.
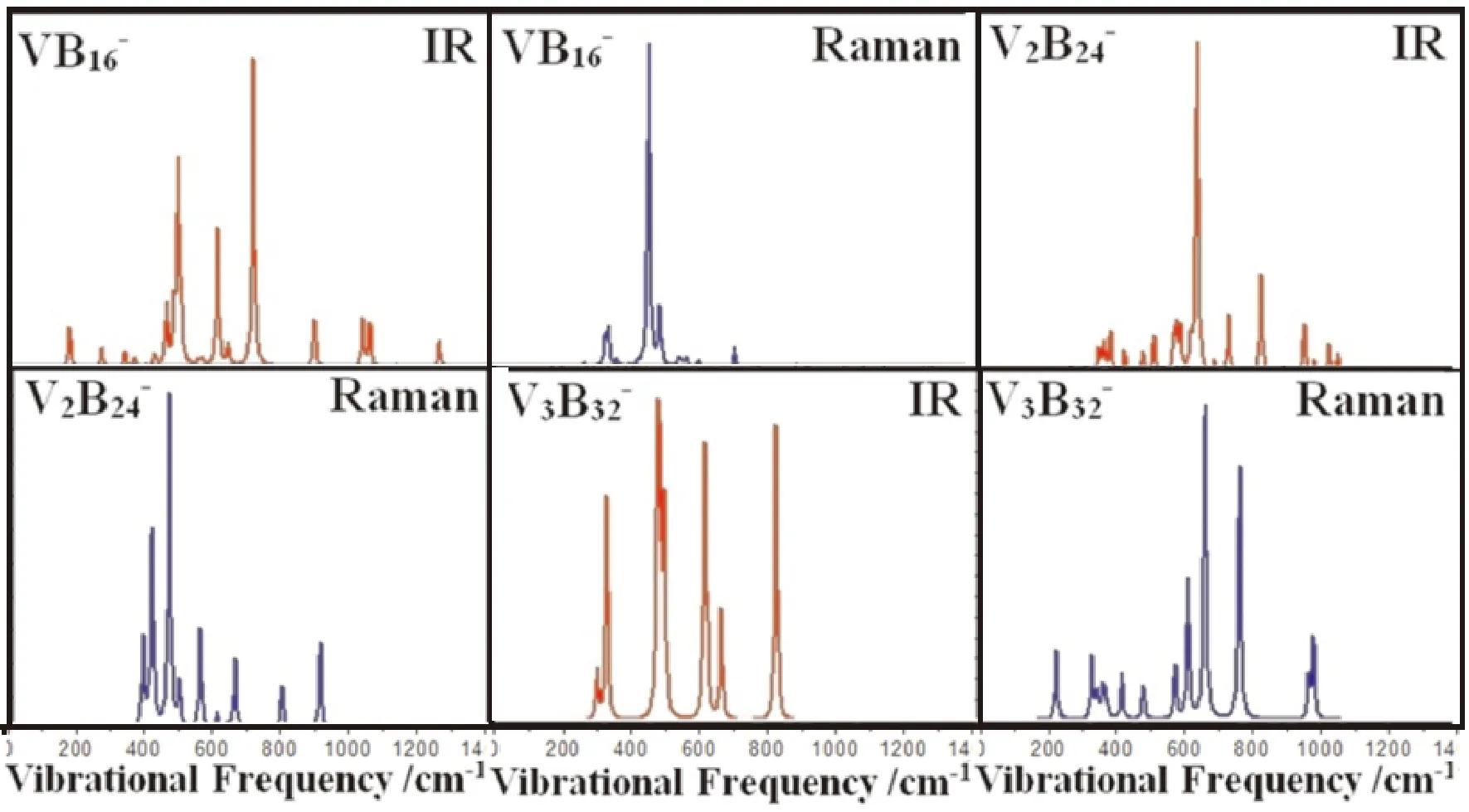
图 4 团簇基态结构对应的红外和拉曼光谱Fig. 4 Simulated IR and Raman spectra of VnB8(n+1)-(n=1-3) clusters
