基于改进U-Net的量子点STM图像分割

王 阳, 丁 召, 宋家勇, 赵广文, 边历峰, 杨 晨

(1. 贵州大学 大数据与信息工程学院 半导体功率器件可靠性教育部工程研究中心, 贵阳550025; 2. 中国科学院 苏州纳米技术与纳米仿生研究所 纳米器件与应用重点实验室, 苏州 215123)

1 引 言

量子点纳米结构具有独特的光电特性，是新型光电材料研究的热点[1]. 在量子点材料研究过程中，可通过扫描隧道显微镜(Scanning Tunneling Microscope, STM)图像对量子点数量、纵横比等表面特征进行定性定量的分析，进而实现量子点材料量子尺寸效应、表面效应等特性的评估[2-4]. 利用STM图像识别量子点特征参数，需要对图像进行分割. 确定量子点像素坐标，将其从复杂背景中分离[5]. 分割后的图像由于量子点像素坐标确定，有利于定性定量分析. 同时，没有复杂背景的干扰有利于节约运算成本.

鉴于图像分割对量子点定性定量分析的意义，诸多研究者在量子点STM图像分割方面展开了研究. 经典的STM图像分割以阈值算法为主要代表[6, 7]. Tripathi等人利用Otsu分割算法结合高斯曲线拟合，实现对不同贵金属亚单层修饰衬底表面STM图像的分割，并将该算法成功用于衬底表面STM图像中簇层的检测[8]. 为了解决Otsu算法自动化阈值分割的盲目性，Ilya Valmianski等人在研究中尝试使用手动阈值分割的方法对STM进行分割，该方法采用预标识手段对目标区域进行约束，以降低无关背景对目标的干扰，可有效提升了STM图像的分割质量[9]. 2019年，Tang等人利用自适应阈值分割对量子点及GaAs(001)衬底 STM图像进行分割，并取得了明显优于传统阈值分割的结果，进一步实现了STM图像分割的自动化处理[10]. 2020年，Kevin Bui等人使用变分方法和经验小波算法对STM图像进行分割，并在以石墨烯等材料的STM图像测试数据中，取得了优于Otsu方法及K-mean方法的效果[11].

而基于深度学习网络的图像分割，具有分割精度高、面对复杂背景识别能力强等优势，近年来被大量应用于显微镜图像分割等领域. 在STM图像特征提取方面，不少研究取得了显著的成果. 2019年，Kamal Choudhary等人通过CNN网络模型在STM图像中识别出材料Bravais晶格[12]. 成功将其与背景分割，有效提升了STM图像的识别精度. 2020年，Maxim Ziatdinov等人使用深度学习技术，通过STM图像分析了H-Si(001)2×1表面原子和缺陷[13]. 克服了传统阈值分割面对复杂背景分割能力弱的困难，对不同缺陷的识别率有显著的提升.

可以看出，神经网络方法成为STM特征提取的研究热点. 为进一步拓展神经网络在STM图像分割中的应用，文章首先采用色彩通道权重灰度化方法对STM图像进行预处理，在实现数据降维的同时尽可能保留量子点信息. 其次，结合U-Net结构特征引入过渡层对其进行改进，使得网络更适合量子点图像的分割. 然后，设计实验对改进网络性能进行检测. 最后，将不同算法分割结果用于量子点STM图像特征识别，根据特征识别结果检验分割精度.

2 算法设计

为了实现量子点的分割，对其STM图像进行处理，主要流程如图1所示：

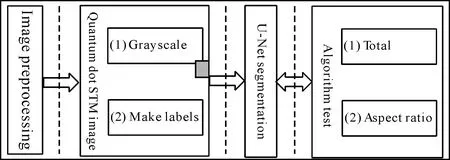
图1 量子点特性参数分析主要流程Fig. 1 The main process of quantum dot characteristic parameter analysis

图1为实现量子点STM图像分割的主要流程. 主要包括图像预处理、图像分割及算法测试三个部分. 首先对图像进行灰度化处理，降低数据维度. 其次，利用降维后的图像数据制作神经网络标签. 进一步，改进U-Net对其进行分割. 最后将连通域统计、最小外接矩形标识应用于量子点数量、纵横比的计算，并用于验证不同算法图像分割质量.

2.1 图像预处理

将原始图像转为PNG (Portable Network Graphics, PNG)格式，并缩放到512*512尺寸. STM图像为RGB(Red Green Blue, RGB)色彩模式的伪彩色图像，数据冗余度大. 为提升算法效率，在分割之前对图像进行灰度化处理，以节约运算成本. 为了降低数据降维带来的信息丢失，采用一种改进的灰度化方法对STM图像进行灰度化处理. 并利用灰度化后的图像制作网络标签数据集.

2.1.1灰度化

RBG图像I(m,n,3)可视为由R(m,n)、G(m,n)、B(m,n)三个像素通道所组成. 对于伪彩色图像，不同对象的色调不同，因而R、G、B三个通道所包含的图像信息不同. 要保证分割质量，灰度图像中相同属性像素区域灰度值应当尽可能相近，不同对象间灰度值差异应尽可能大[14, 15]. 根据STM伪彩色图像特点，采用一种权重赋值法对图像进行灰度化.

首先，定义图片像素值总和为：

(1)

式(1)中T表示整张图像各个像素点三个通道像素值累加和，定义各个分量相对整张图像的占比为Ak(k=1, 2, 3)，则其满足：

(2)

式(2)中Ak为不同分量相对整张图像所占比重，当k= 1、2、3时分别表示R、G、B分量在整张图像的权重. 定义灰度图像为IG(m,n)，对任意像素点，其灰度值满足：

(3)

式(3)表示通过图像R、G、B分量所占权重对像素进行降维. 在伪彩色图像中，权值较大通道下所包含的图像信息更丰富，该方法有助于突显包含图像信息更多的通道像素值，降低数据降维带来的信息损失.

2.1.2数据集制作

选取120张灰度化后的STM量子点图像制作标签形成数据集. 标签制作中，采用人工方法对量子点像素区域进行预标记. 为进一步提升标签精度，将预标记图像交由3名专业量子点材料研究人员进行校正，综合校正结果，对像素点归类存在争议的区域，选取研究人员标记众数对其进行归类. 标签及测试样本如图2所示：

图2 数据样本. (a)标签原图；(b)训练样本；(c)标签；(d)测试样本Fig. 2 Data samples. (a) Original label; (b) Training sample; (c) Label; (d) Test sample

2.2 图像分割

2.2.1 改进U-Net分割算法

对量子点图像进行分割. 针对STM图像中量子点尺寸及形态多变，边缘像素与背景差距小的问题，本文采用改进U-Net结构实现其分割. 原始U-Net结构由Ronneberger等人在2015年根据FCN结构发展而来[16, 17]. 原始网络结构可理解为由编码器和解码器两部分组成，编码器部分通过3×3的卷积层和一个2×2的池化层向下提取特征. 解码器部分则实现上采样功能. 本文在原始网络中引入过渡层，以期提升U-Net在量子点STM图像分割上的精度，其结构如图3所示.

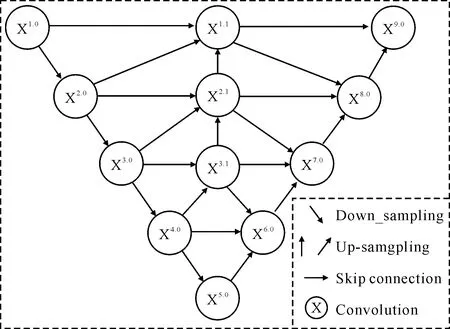
图3 改进U-Net结构Fig. 3 Improved U-Net structure

由图3可知，在经典的U-Net结构上做出了如下改动：首先，相对原始网络，改进网络增加了中间过渡层. 该网络对4.0、3.0、2.0层进行上采样，拼接并融合前层特征得到中间过渡层；其次，在过渡层中引入下采样，将3.1、2.1、1.1等过渡层特征下采样并分别与6.0、7.0、8.0层拼接，构建出具有过渡层的U-Net网络结构. 一方面，不同感受野的深度特征可以依靠过渡层向上传递. 另一方面，浅层特征也可进一步向下传递，使得量子点边缘像素特征得到增强，有助于分割. 改进后的网络各层信息利用更加全面，对边缘像素辨识度更好.

3 实验结果与讨论

3.1 灰度化算法对分割精度的影响

对缩放后的STM图像进行灰度化处理，其效果如图4所示. 可以看出改进的RGB权值灰度化算法灰度图像中量子点像素区域整体灰度值差异较小，灰度值层次明显. 同时，细节信息更为丰富，量子点边缘像素保存相对完整.

图4 不同灰度化算法对比：(a)样本原图；(b)RGB权值；(c)rgb2gray；(d)均值；(e)最小值Fig. 4 Comparison of different grayscale algorithms: (a) Original picture of sample; (b) RGB weights; (c) rgb2gray; (d) Mean value; (e) Minimum value

进一步，为测试灰度算法对分割的影响，利用Keras框架构建了图3所示改进U-Net模型，并基于Tesla k40c GPU平台进行训练与验证. 根据训练结果，构建混淆矩阵. 统计模型将正例识别为正例、正例识别为负例、负例识别为正例、负例识别为负例等情况，计算出模型准确率、召回率及F-meaure值. 从表1实验结果可以看出，改进灰度化算法下图像分割评价指数相对高于rgb2gray、平均值及最小值等方法. 结合表1及图4可以看出，由于改进灰度化算法保留量子点边缘区域像素更加完整，更有利于量子点边缘像素的分割.

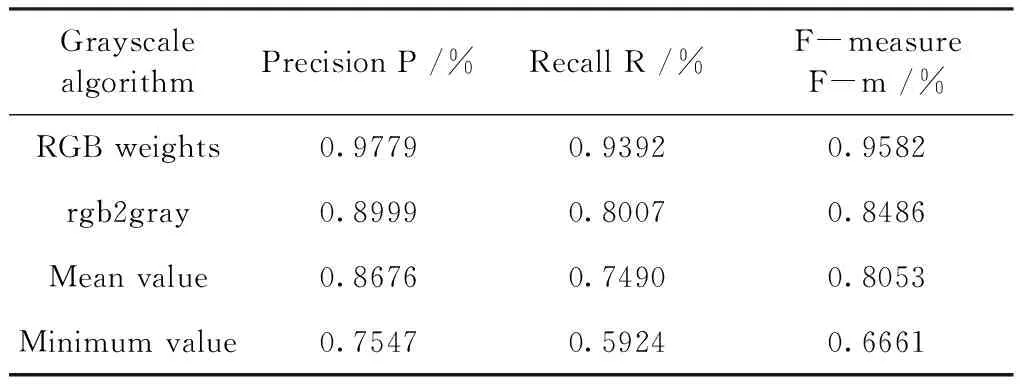
表1 不同灰度算法分割结果平均值

3.2 分割结果与分析

利用RGB权值灰度化后，将图像送入原始与改进U-Net模型进行对比测试. 每次以3：2的比例随机选取标签及测试数据进行交叉测试，结果如图5所示.

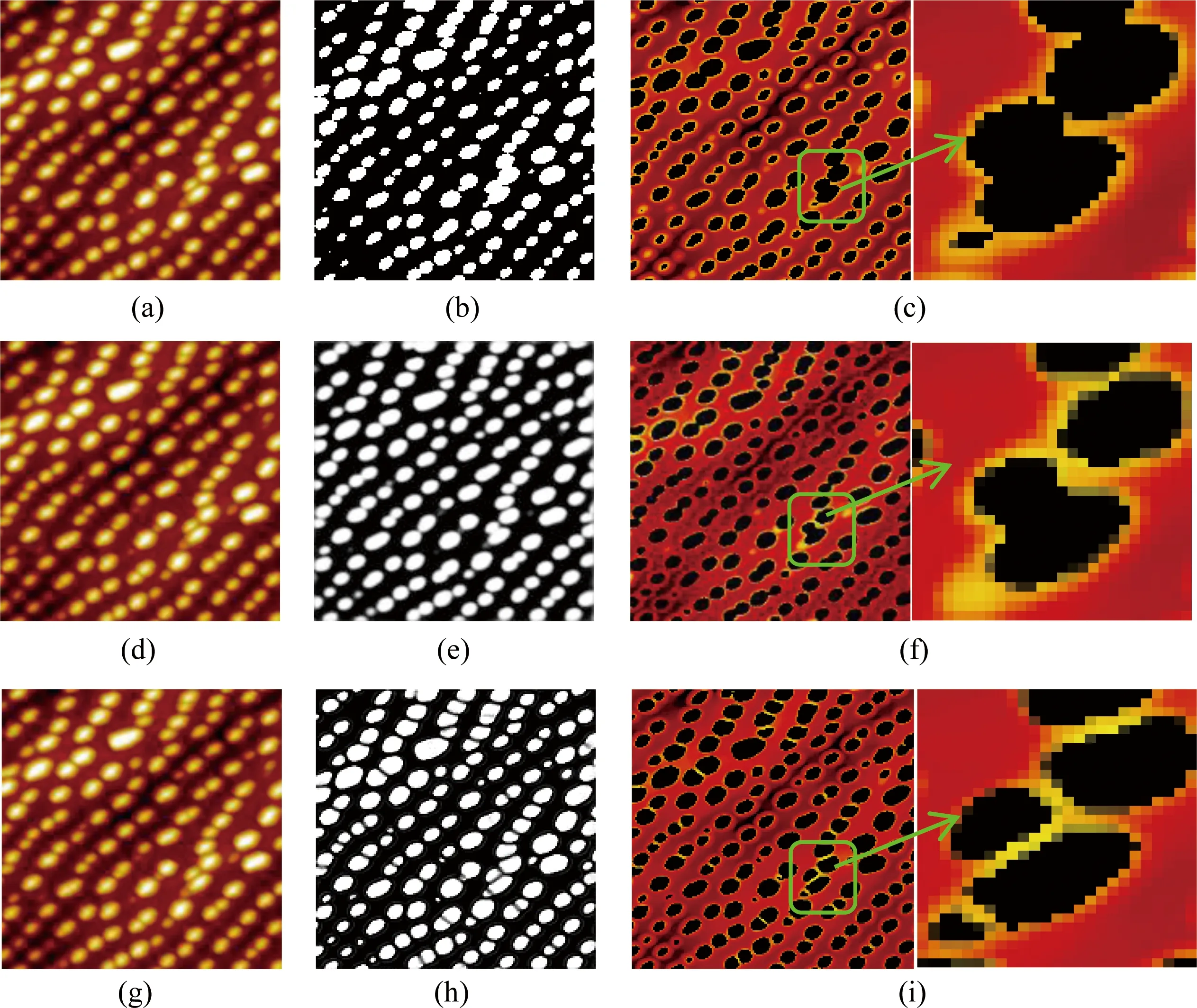
图5 分割效果对比. (a) (d) (g) 样本；(b) (e) (h) 分别为阈值、原始U-Net分割和改进U-Net分割结果；(c) (f) (i) 叠加对比Fig. 5 Comparison of segmentation effects. (a) (d) (g) samples; (b) (e) (h) are threshold, original U-Net segmentation and improved U-Net segmentation results; (c) (f) (i) overlay comparison

图5(a)背景较为复杂，存在大量深色沟壑，属于背景较为复杂的量子点STM图像. 其中量子点尺寸差异较大，边缘像素值强度较低. 从图5(b)、(c)可以观察到传统阈值分割算法分割精度较低，部分像素值较弱的量子点没有被识别，边缘像素分割粗糙，量子点间存在较为严重的像素重叠. 对比图5(e)、(f)可以看出，采用原始U-Net网络会提升分割精度，但仍然存在小尺寸量子点未能识别及量子点粘连现象. 而改进后的U-Net(图5(h)、(i))使分割质量进一步改善，其中小尺寸量子点区域的识别较为精确，且分割后量子点边缘像素相对平滑，量子点间无明显像素重叠.

统计8次交叉测试的结果如图6所示. 可以看出，改进网络Precision平均值为97.79%，Recall平均值为93.92%，高于原始网络的83.96%与91.76%. 表明改进网络拥有更高的像素分类正确率及量子点像素识别正确率. 此外，改进网络的两者调和平均数F-measure为95.82%，高于原始网络的87.69%. 因此，改进U-Net分割方法相对于传统分割方法，具有更高的边缘像素分割精度.

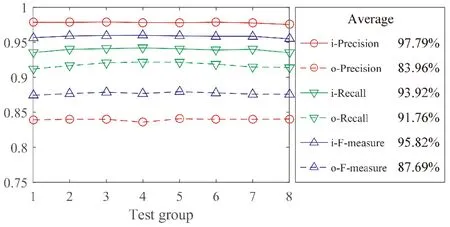
图6 交叉测试结果, “ i ”：改进网络; “ o ”：原始网络Fig. 6 Cross test results, " i ": improved network; " o ": original network

3.3 特征参数识别结果

为验证分割结果对后续特征参数提取的影响，本文进一步利用连通域统计算法与基于顶点链码-离散格林理论的最小外接矩形标识法对量子点数量、纵横比进行分析.

3.3.1数量统计

将不同分割算法处理后的二值图像利用连通域算法进行量子点数量统计[18]. 如前所述，改进U-Net降低了量子点边缘像素重叠，同时提升了小尺寸量子点识别精度，因此在表2所示的实验结果中，改进U-Net提供了更高的量子点数量识别精确度.

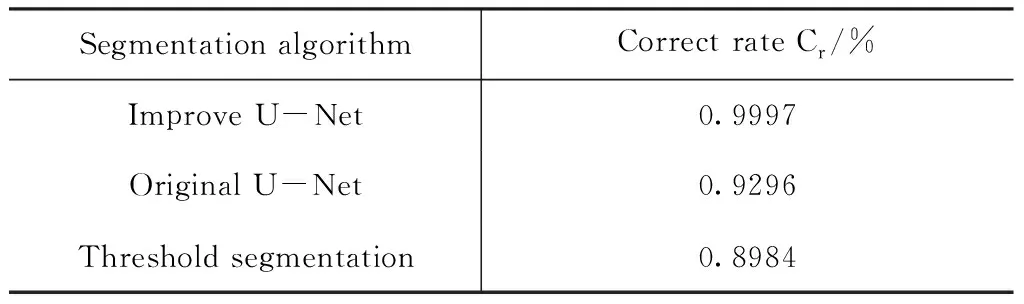
表2 量子点数量统计结果

3.3.2纵横比计算

量子点纵横比指量子点长轴与短轴比值. 在测试集分割结果中，针对标签、改进U-Net、原始U-Net及阈值算法分割结果，分别利用顶点链码结合离散格林理论对量子点做最小外接矩形标记[19]. 标记结果如图7所示.

图7 最小外接矩形标记Fig. 7 The smallest circumscribed rectangle mark

通过对比标签与三种算法分割结果最小外接矩形标识结果可以观察到，改进U-Net边缘分割更加精确，因而量子点边缘与标签契合度高，最小外接矩形更为接近. 图8给出了不同分割方法计算所得长宽比相较于标签值的误差，可以看出，改进U-Net平均误差为2.06%，原始U-Net为4.30%，Otsu算法为10.17%，说明改进网络的分割提升了量子点纵横比的识别准确度.

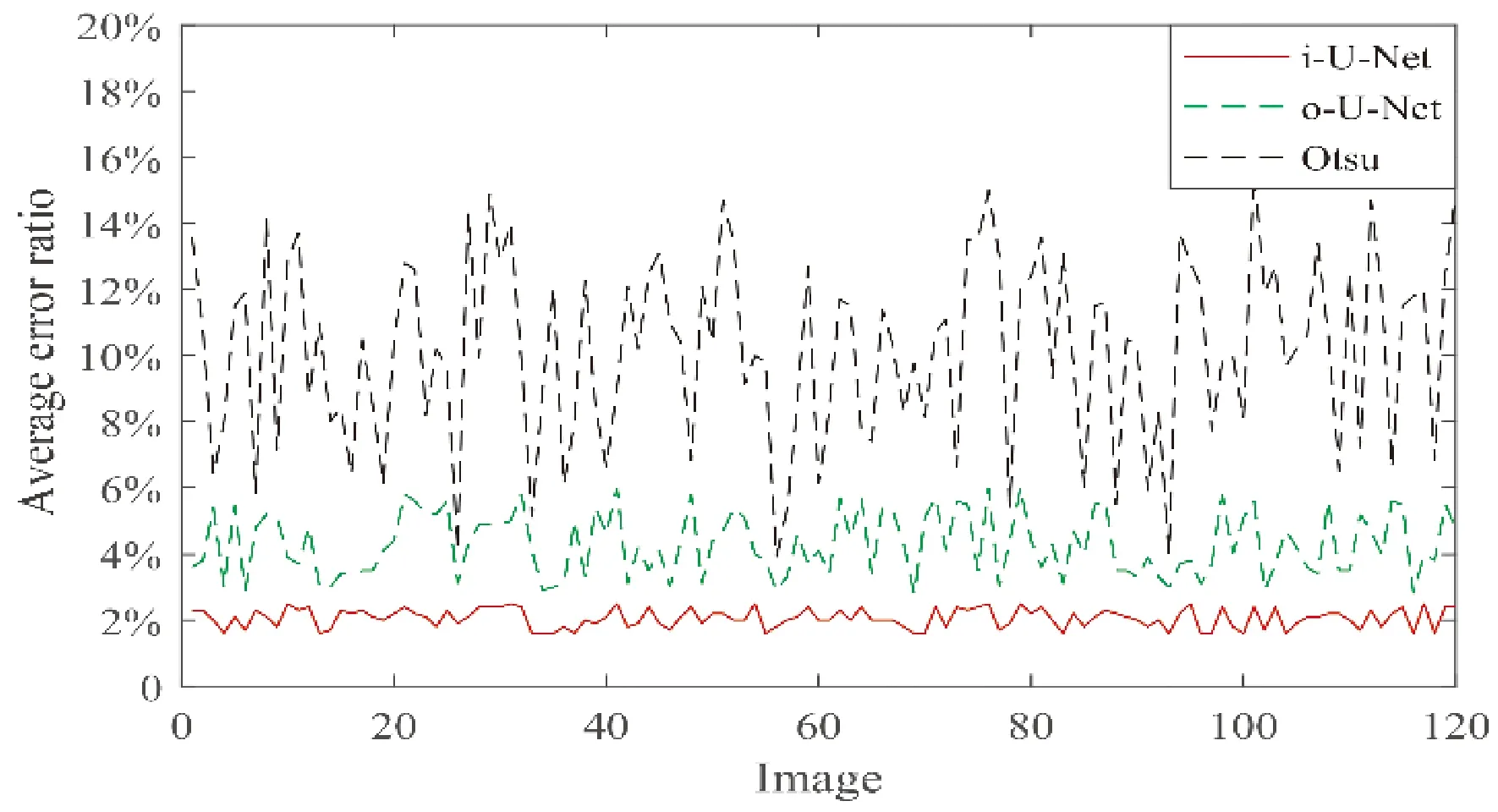
图8 纵横比误差统计Fig. 8 Aspect ratio error statistics

4 结 论

为提升量子点STM图像分割质量，改进U-Net算法对量子点STM图像进行分割. 首先，对量子点STM图像进行了预处理. 通过对不同灰度化算法降维后的数据进行分割对比，改进灰度化算法降维下量子点分割Precision、Recall、F-measure指数相对优于rgb2gray、均值、最小值等算法. 其次，在U-Net网络中引入过渡层，对量子点图像进行分割. 改进后的网络训练结果Precision、Recall、F-measure分别为99.85%、93.54%、94.05%，相对高于原始网络结构13.83%、2.16%、8.13%. 最后，对阈值算法、原始U-Net、改进U-Net分割结果进行量子点数量及纵横比统计，改进U-Net分割结果有效提升了小尺寸量子点识别能力，并降低了像素重叠现象. 量子点数量识别精度达到99.97%，纵横比平均误差为2.06%，对比原始U-Net及Otsu算法识别结果有所提升. 因此，改进U-Net的量子点STM图像分割是一种提高量子点特征识别精度的潜在手段.