基于均值半绝对偏差的一种投资组合最优化模型

瑛 瑛

(呼伦贝尔学院 内蒙古 海拉尔 021008)

1 引言

现代投资组合理论是基于马科维茨(1952年)[1]的工作。马科维茨利用方差作为风险度量把投资组合选择问题数量化。在1991年，Konno和Yamazaki[2]首次提出以均值绝对偏差(MAD)为风险度量的投资组合选择问题的线性规划模型。在1993年，Speranza[3]利用均值半绝对偏差代替MAD并指出该风险度量等价于MAD，又减少了数学规划模型中的约束个数。同年，Feinstein和Thapa[4]又独立地提出这两个风险度量的等价性。利用均值半绝对偏差度量风险比方差度量风险更加科学合理，因为在进行投资时，往往只担心收益率低于期望收益的部分，只有低于期望收益率的投资才会带来风险[5]。

一般，在实际的投资组合中，股票的单位数必须是整数,又结合我国证券市场实际情况，本文考虑一种带有固定交易费用和整数交易单位的投资组合，以均值半绝对偏差为风险度量建立了混合整数线性规划模型。

2 模型建立

假设一个投资者在种证券中分配他的资金，收益率是随机的。令N=1,2,…,n表示有价证券集合，定义R=(R1,R2,…,Rn)为表示n种证券收益率的n个随机变量组成的向量，均值为rj=E[Rj]，j∈N.又假设每个随机变量Rj,j∈N是离散的，它的值由其在特定场景下的实现值给出。

均值半绝对偏差是指投资组合的实际收益率低于平均收益率的绝对值[6]，将其简单地称为均值半偏差，可表示成数学表达式

γ(X)=E[mzx{μ(x)-Rx,0}]

(1)

均值半偏差等于均值绝对偏差的一半，即

因此，相应的均值半绝对偏差模型等价于MAD模型。因为离散随机变量是由其实现值表示的，所以，式(1)的均值半偏差为实现值μt的凸分段线性函数，也是投资组合X本身的凸分段线性函数，且LP可计算的，如：

使yt≥μ(x)-μt，yt≥0，对t=1，…，T.

(2)

其中非负变量yt表示场景t=1,…,T下的下行偏差。

引入一些附加的符号。设g表示证券投资所得税，且cj,j∈N表示选择证券j时投资组合的固定交易费用。定义Sj,j∈N为证券j,j∈N在投资组合选择日的报价，令uj表示为证券j所购买的股票单位数量的上界。一般，单个证券投资的上界是以其日平均交易量的百分比计算。当这些信息无法获得时，每个证券j的最大股票单位数可近似计算为[c/sj]，其中c是可用于投资的资金。μ0表示投资者要求的最低收益率。当μ0=0时可得到所谓的最大安全投资组合。

每个变量xj,j∈N表示证券j选择的股票单位数。变量zj,j∈N为二进制变量，能够表示证券j的交易费用[7]。仅当证券j被选择时产生固定费用cj.即

(3)

当考虑固定交易费用、实现收益的税和整数交易单位时，最大安全投资组合问题可以表述为以下混合整数线性规划问题：

(4)

(5)

(6)

(7)

xj-ujzj≤0,j=1,…,n

(8)

yt≥0,t=1,4,…,T

(9)

xj≥0整数j=1,…,n

(10)

zj∈{0,1},j=1,…,n

(11)

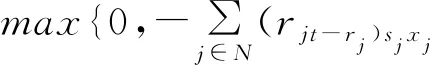
3 数值分析

首先，选取沪深股市30只股票涉及到不同的行业，下载了从2019 年 11 月 28 日至 2020 年 4 月 1 日90个交易日的日线于Excel表格中，计算出每只股票的日收益率及其平均值[8]，并以这些数据为样本，创建了三个数据集nd1,nd2,nd3。所有股票的固定交易成本水平设定为一个常数，即cj=c,∀j∈n.在第一和第三数据集的情况考虑固定成本等于2，第二数据集考虑固定成本等于0.5，假设三种情况投资资本的价值都等于2000。

我们已经在CPLEX20.1.0测试了数据集及投资组合模型的有效性。在本次实验中，假设g=0.06,λ=0.01,μ0=0.

表1 数据集1中十种股票的日收益率均值

表2 数据集2中十种股票的日收益率均值

表3 数据集3中十种股票的日收益率均值

表4 三种数据情况下最优投资策略

计算结果表明，取三种不同数据集的情况下，都得到了整数最优解集。每个整数表示三种情况最优投资组合中相应股票的个数，收益和风险分别表示三种情况下最大收益和最小风险值。由于考虑股票的时间段正是我国新冠肺炎疫情比较严重的时期，投资收益普遍低，尤其第二组数据所有股票表现都不好，在这种情况下已得到了最优解表明本文建立的投资组合模型是合理有效的，在实际投资中有一定的指导作用。