区域电热综合能源系统稳态潮流建模与算法研究

李卓然，南君培，王 超，孙 可，周 浩

（1.浙江大学 电气工程学院，浙江 杭州310027；2.国网浙江省电力有限公司，浙江 杭州310007）

0 引 言

温室气体[1]排放的最大贡献来自能源供应中的煤炭、天然气和石油的燃烧发电和供热。为了实现减少温室气体排放量，必须大幅增加可再生能源的利用效率。随着可再生能源[2-3]的区域电热综合能源系统中以燃气轮机、分布式能源站为代表的城市天然气应用工程加速天然气网络的扩展，燃气轮机发电站点的建设以及天然气网络的扩张，电-气互联综合能源系统将成为未来重要的供能系统。同时，电转气装置（power to gas，P2G）的出现进一步促进了电网和天然气网络的融合与耦合。但由于当前电力网络及天然气网络的能流管理及调度分属不同主体，其联合调度受到了物理因素的制约。

对区域电热互联的综合能源系统合理建模与求解，从而获取电热互联的区域综合能源系统的稳态运行方式，对于电热系统规划、优化运行、事故检修以及静态安全分析[4]都有着重要指导作用。

本文提出了一种电-热互联综合能源系统稳态模型，能够较为准确地获取考虑电热耦合的综合能源系统的电热潮流[5]数据。以巴厘岛电热综合能源系统算例验证了模型的准确性，并在求解过程中比较了P-Q分解法和Fsolve两种求解算法的优劣。

1 区域电热综合能源系统稳态潮流模型

1.1 热力系统水力模型

水力模型约束方程描述为：

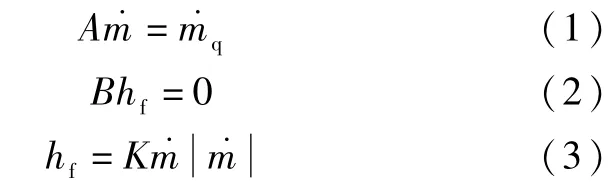
式中：A为网络矩阵；˙m为管道流量；˙mq为节点负荷流量；B为回路矩阵；hf为管道压降；K为管道阻力系数。

1.2 热力系统热力模型

热力模型约束方程描述为：

式中：Φ为热负荷；Ts为供水温度；To为回水温度；Tstart为管道首端温度；Tend为管道末端温度；λ为传热系数；min为流入节点管道流量；mout为流出节点管道流量；Tin为管道末端的温度；Tout为混合温度。

1.3 电热耦合元件模型

电热耦合元件的代表是热电联产机组[6]，由燃气轮机及发电机与余热锅炉、蒸汽轮机或供热式蒸汽轮机（抽汽式或背压式）共同组成的循环系统，它将燃气轮机做功后的高温乏烟气热量通过余热锅炉回收转换为蒸汽热量，蒸汽注入蒸汽轮机发电，或将部分发电作功后的乏汽用于供热。

根据热电联产机组的热电比是否随着出力改变，可以分为定热电比和变热电比机组两类。

式中：φCHP是CHP机组的热出力；PCHP是CHP机组的电出力；η为CHP机组冷凝效率；Fin为燃料输入速率；Cm为一恒定量；CZ是随着燃料输入速率变化的量。

2 算例分析

本文以巴厘岛电热模型[7]为例。如图1所示，巴厘岛电热模型为32节点热网，9节点电网通过3台热电联产机组耦合组成。

图1 巴厘岛电热模型系统结构图

其中，CHP1和CHP3为定电热比热电机组，热电比参数如表1所示。

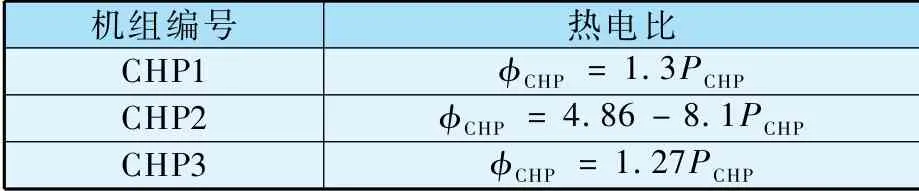
表1 机组热电比参数

电网基准功率为1 MW，基准电压为11 kV；导线每千米阻抗为z=（0.164+j0.08）Ω；主变压器采用33/11.5 kV，额定容量15 MVA，额定电压百分数为18%；母线I、III、IV、V和VI的有功负荷分别为0.2 MW、0.5 MW、0.5 MW、0.2 MW、0.2 MW；各用电负荷功率因数为1；三个电源电压幅值为分别为1.02pu，1.05pu，1.05pu；电源1的电压相角为0°；电力管道长度如图1所示；电力节点IX为平衡节点。

热网总负荷为2.164 MW，节点1、31和节点32分别对应三个电源CHP2、CHP1和CHP3；CHP3的电出力P3=0.3 MW，根据机组3的热电比可以求出机组3的热出力φCHP3=0.3797 MW；热力管网供热温度为70℃，热力管网回水温度为30℃；管道所在环境温度为10℃；水密度ρ=958.4 kg/m3；水的运动粘度μ=0.294×10-6m2/s；热力管网参数如图1所示；热网节点1为平衡节点。

3 区域电热综合能源系统稳态潮流模型求解方法比较

3.1 运用牛顿拉斐逊法对电热约束方程来回迭代求解的算法

电热互联的牛顿拉斐逊迭代法[8]的求解过程是先根据热网约束中的水力方程计算出一组管道流量m0作为迭代初值；然后之后的循环过程是先由热网约束方程计算出对应的雅各比矩阵J1并带入初值m0得到m1、T、TM；根据管道1的质量流量计算出机组CHP2的热出力，并由机组CHP2的热电比参数得到相应机组CHP2的电出力；然后将机组CHP2的电出力作为已知量，计算电网约束方程的雅各比矩阵并求出电力潮流参数；然后根据求解出的母线2的电出力算出机组CHP1的电出力，并由CHP1的热电比参数机组CHP1的热出力；接着判断所求管道流量等参数是否收敛并满足求解精度；然后将机组CHP1的热出力作为已知量带入水力热力计算流程开始下一次的迭代过程。牛顿拉斐逊法迭代法的计算流程如图2所示。

图2 牛顿拉斐逊法迭代法求解稳态潮流的流程示意图

3.2 运用Fsolve函数统一处理电热非线性方程组的算法

Fsolve函数的电热互联系统的稳态潮流求解算法流程上与牛顿拉斐逊法迭代法的求解过程类似。不同的是：（1）迭代初值需要自己设定并且初值的选取可能直接影响到结果是否收敛。选取不同的初值对求解的结果影响较大，初值选取的不合适可能会导致不收敛的问题。（2）省去了计算非线性方程组对应的雅各比矩阵继而去求解每一次的迭代结果的步骤。Fsolve函数可以直接求解非线性方程组，计算速度相对较快。Fsolve函数求解电热系统稳态潮流的流程如图3所示。

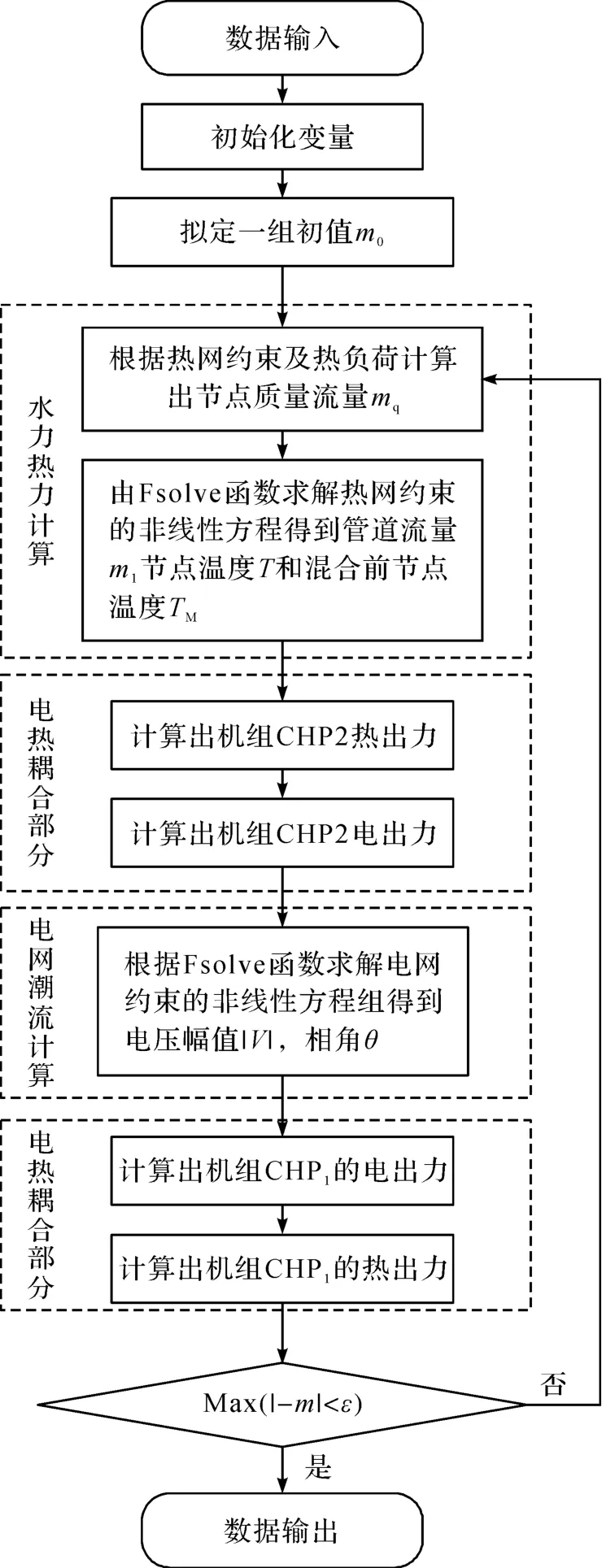
图3 Fsolve函数求解电热系统稳态潮流流程示意图

4 算例结果分析

4.1 稳态潮流结果分析

运用牛顿拉斐逊法对电热约束方程来回迭代求解的算法，软件为MATLAB，计算机参数为Intel core i5-8300H，2.30GHz，16GB，运行时间为27.5s。求得的巴厘岛电热互联系统的热力参数和电力参数如表2和表3所示。其中，以文献[7]中SINCAL软件仿真值作为对照。

表2 所求热网管道流量与实际管道流量数据对比

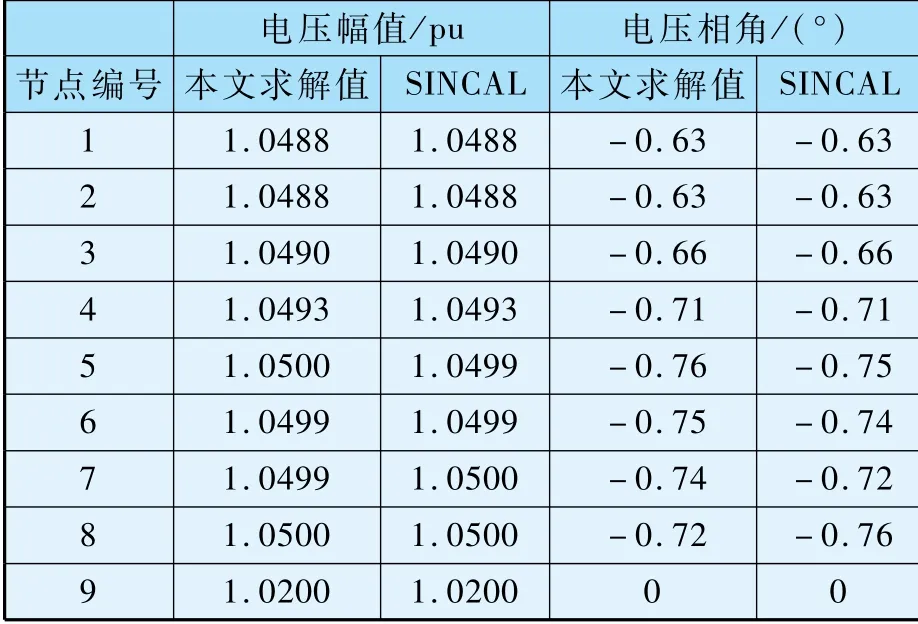
表3 电压幅值和相角与实际值数据对比

从表2、表3所示电网和热网数据来看，通过牛顿拉斐逊迭代法对电热互联的综合能源系统的求解的电力热力参数非常准确，考虑电热耦合的区域电热互联的综合能源系统模型的建立与求解比较合理。

4.2 两种求解算法结果比较分析

为了进一步比较和研究两种求解算法，预设了管道流量的三组初值用Fsolve函数的电热互联系统的稳态潮流求解算法。管道流量的三组初值分别设定为1kg/s，-1kg/s和0kg/s，每组运行时间约8s，结果如表4所示。其中，以文献[7]中SINCAL软件仿真准确值作为对照。

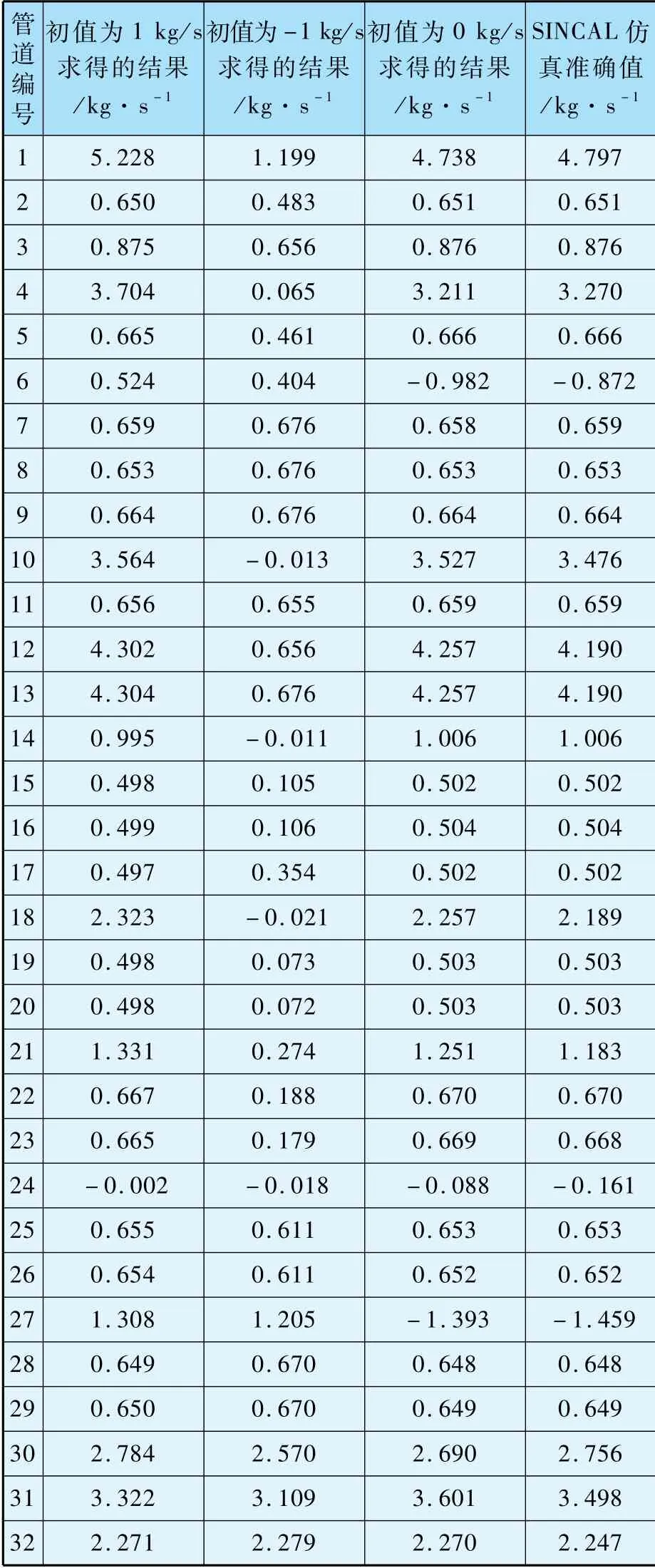
表4 Fsolve函数计算的三组稳态潮流结果对比

由表4数据可以看出，1 kg/s，-1 kg/s和0 kg/s分别作为初值用Fsolve函数求解时，0 kg/s作为初值得到了与文献[7]中SINCAL软件仿真准确值相一致的仿真结果，而1 kg/s和-1 kg/s作为初值得到的结果与SINCAL软件仿真准确值不吻合。由前面计算结果，运用牛顿拉斐逊法对电热约束方程来回迭代求解的算法的单次运行时间平均为27.5 s，而用Fsolve函数的电热互联系统的稳态潮流求解算法单次运行时间平均为3.9 s，可知Fsolve函数求解速度较快，但初值的选取对Fsolve求解结果影响较大。

5 结 论

本文对考虑电热耦合的综合能源系统进行建模，将巴厘岛电热模型作为算例验证了模型的合理性，并利用牛顿拉斐逊法准确求解出电热综合能源系统的稳态潮流。同时，通过比较牛顿拉斐逊迭代法和Fsolve函数求解算法的优劣，认为牛顿拉斐逊迭代法不需要给定初值，但求解时间相对较长，Fsolve函数求解算法求解速度快，但对初始值的选取较为严格。