基于动态负荷预测的配电网动态状态估计方法
2021-09-16潘敦辉董丽澜郭瑞鹏
黄 昭,潘敦辉,董丽澜,郭瑞鹏
(1.浙江大学 电气工程学院,浙江 杭州310058;2.杭州沃瑞电力科技有限公司,浙江 杭州310027)
0 引 言
配电网状态估计利用系统采集的测量数据来估计系统的运行状态,对配电网运行的分析和管理具有重要意义。传统的电力系统状态估计是一个静态估计问题,多采用加权最小二乘(weighted least squares,WLS)方法求解。随着相量测量单位(phasor measurement unit,PMU)部署在系统中[1],测量数据更新频率大大提高,电力系统动态状态监测已经成为可能。电力系统动态状态估计(dynamic state estimation,DSE)可以由历史状态数据估计下一时刻状态,再用量测数据进行修正,所以更适合实现电力系统状态的动态跟踪[2]。
电力系统动态状态估计多为扩展卡尔曼滤波(extend Kalman filter,EKF)状态估计[3],虽然目前EKF有许多改进方法[4],但EKF有其局限性,即在计算Jacobian矩阵时不可避免地引入线性化误差[5]。容积卡尔曼滤波(cubature Kalman Filter,CKF)基于数值积分理论[5],通过选取确定的采样方法来近似非线性分布,进而解决非线性问题,滤波精度在二阶以上。同时相比Julier等提出的无迹卡尔曼滤波(unscented Kalman filter,UKF)算法[7],CKF算法有严格完整的理论基础,具有更好的数值稳定性。因此本文引入CKF实现电力系统动态状态估计计算。目前,大多数电力系统动态状态估计算法在状态预测步骤中采用指数平滑法直接对状态变量进行线性外推[8]。然而这一过程,并不符合电力系统运行规律。实际上,状态量的变化是节点负荷以及发电机出力改变的结果。由此,通过母线负荷预测解决状态预测问题更具有现实意义和物理意义。
综上,本文在传统CKF动态状态估计算法基础上,通过引入动态负荷预测(dynamic load prediction,DLP)模型,改进DSE状态预测环节;将预测量作为扩展状态变量,在量测方程中加入预测量与状态量之间的等式约束关系;针对配电网特点提出基于动态负荷预测的配电网动态状态估计方法。最后用文献[9]所提IEEE119节点配电系统模型数据设计仿真算例,验证了算法有效性。
1 容积卡尔曼滤波原理
电力系统中的状态方程和量测方程可用如下形式表示:

式中:k为离散时间,xk为系统在k时刻的状态变量,zk为对应状态的观测信号,f(~)是状态方程;h(~)是量测方程;wk为k时刻系统过程噪声序列,vk为k时刻系统观测噪声序列。
设wk和vk是互不相关的均值为零的高斯白噪声,且具有时变统计特性,即

其中,Rk表示k时刻量测噪声方差矩阵,由各量测设备和量测类型决定。Qk表示k时刻过程噪声方差矩阵,由状态模型准确程度决定。N(μ,δ2)表示均值为μ方差为δ2的高斯噪声。
1.1 容积变换过程
容积变换[6]是基于三阶球面径向容积准则选择适合的采样策略来选取一组容积采样点,使选取的采样点均值和协方差原状态分布的均值和协方差,将采样点进行非线性变换,使得变换后的均值和协方差逼近附加高斯噪声的非线性系统的状态均值和协方差,是理论上当前最接近贝叶斯滤波的近似算法。
对于非线性变换y=f(x),状态变量x为n维随机变量,其CKF采样点和相应权值选取如下:

其中,ξi取式(5)中的第i个n维列向量,代表第i个采样点;wi代表与第i个采样点对应的权重值。
1.2 CKF滤波过程
(1)状态预测
xk-1为k-1时刻状态量,Pk-1|k-1为k-1时刻状态量的协方差,由式(4)(5)得到Cubature点集和对应的权值,由非线性变换y=f(x)得到一步预测点,及一步预测协方差。

根据一步预测值,再次进行容积变换,产生容积点并代入量测方程,得到量测预测值:
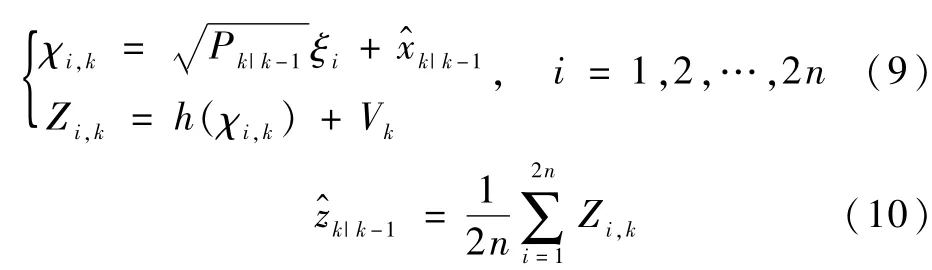
其中,Zi,k表示k时刻量测预测值对应的容积点;表示k时刻量测预测值。
(2)滤波更新
由经过量测方程传播得到的量测预测点Zi,k和量测预测值算出新息协方差矩阵Pzz,k和状态量测交叉协方差矩阵Pxz,k:
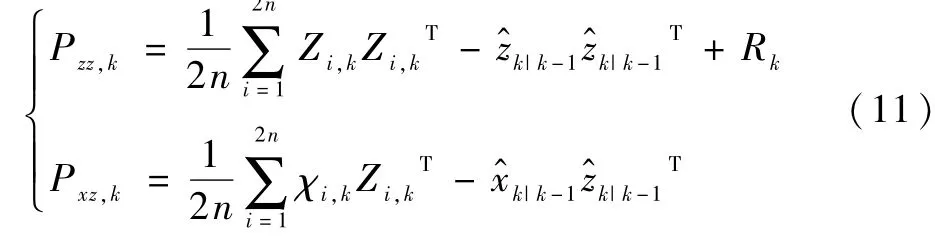
最后通过式(12)求解卡尔曼增益Kk,结合量测实际值zk和量测预测值z^k|k-1求得修正量,对状态预测值进行后验校正,并完成协方差矩阵更新,得到当前状态估计结果,见式(13)至式(14)[12]。

2 动态负荷预测
2.1 两参数指数平滑负荷预测
电力系统状态估计中,一般把节点电压幅值和节点电压相角设为状态变量,即:x=[V,θ]T。在动态状态估计的状态预测环节需要通过状态方程,由k时刻状态量xk预测下一时刻系统状态xk+!。由于电力系统的模型参数具有不确定性,所以尚无准确的状态方程建模方法。目前电力系统DSE大多采用指数平滑法直接对状态量[V,θ]T做线性外推。这种状态推测方法虽然在系统稳态运行情况下效果可行,但缺乏理论支撑。因为电力系统状态量是一组因变量,节点电压幅值和相角随系统中节点负荷和发电机出力改变而变化。而电网中负荷与发电机出力的变化是有规律性的。因此,通过动态负荷预测间接获取状态转移关系,从而预测下一时刻系统状态更具可信性和合理性。
在本文探讨的配电网动态状态估计中,基于配电网运行特点做如下假设:
系统中主电源节点的有功出力是其余节点功率注入的函数,可不对其进行预测。选取主电源节点为参考节点,节点电压相角为0;预测向量取为:分别表示除主电源节点外其余节点的有功负荷和无功负荷。

电力系统负荷随时间变化趋势明显,在假定负荷没有跳跃性变化的情况下,可使用趋势外推法进行超短期负荷预测。由于动态状态估计中状态预测过程具有时间粒度小,计算频率高的特点,这里选用两参数指数平滑法,算式如下:其中,α和β表示两参数指数平滑法选取的平滑参数。α表征趋势预测中对近期历史数据的信任度,β表征对远期历史数据的信任度。由于电力系统负荷具有明显的日周期变化规律,因此可通过历史日负荷曲线获得最优平滑参数α,β。实际生产中,供电部门一般只能提供配电馈线根节点的总负荷曲线,而无法提供每台配电变压器负荷曲线。这时计算时,需要根据实际配电网运行特点,计及历史数据,把根节点总负荷按照一定分配系数及各配电变压器额定容量进行分配,再根据所得变压器负荷曲线获得各负荷节点对应平滑参数αi,βi。实际中一般更信任近期历史数据,因此可取:

2.2 预测误差协方差矩阵计算
在基于容积卡尔曼滤波的动态状态估计的状态预测环节引入动态负荷预测后,预测误差协方差矩阵算式需要做出调整。
令Pk-1为k-1时刻状态量xk-1的误差协方差矩阵。由式(4)(5)得到Cubature点集和对应的权值。根据式(15),把采样点集[χi,k-1]变换为对应的负荷采样点集合[Si,k-1]。再由k-1时刻对应的负荷采样点,按照两参数指数平滑法计算k时刻预测负荷采样点集。预 测 负荷采样点 对应的误差协方差矩阵为:
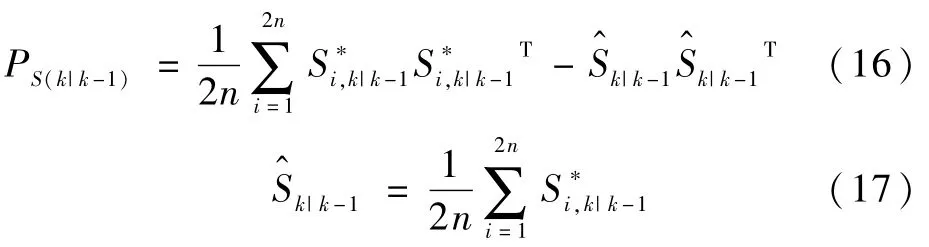
3 基于动态负荷预测的CKF算法
3.1 基于DLP的电力系统动态状态估计算法
在电力系统CKF动态状态估计的状态预测环节引入动态负荷预测后,需通过约束条件使负荷预测信息作用于状态量,以替代传统算法中状态预测步骤所起的作用。因此,本文将负荷预测量S作为扩展状态变量,建立负荷预测向量S与状态向量x的等式约束关系;将负荷预测值作为特殊量测数据;最后通过卡尔曼增益系数将量测信息作用于状态量,完成状态校正,求得状态估计结果。
目前,由全球定位系统(global positioning system,GPS)和北斗卫星导航系统授时的PMU设备正逐步应用在配电网中,但短期尚无法取代SCADA系统提供满足状态估计可观测性要求的量测数据[10]。在一段时间内,采用PMU和SCADA混合量测数据是解决配电网态势感知问题的有效手段[11]。因此,本文所提基于动态负荷预测的配电网动态状态估计算法采用混合量测模型。
基于动态负荷预测的电力系统CKF算法将负荷预测量PL,QL作为扩展状态变量,因此状态空间为:[x,S]T,其中x=[V,θ]T,S=[PL,SL]T。
负荷预测向量S与状态向量x存在等式约束关系S=g(x)如下:
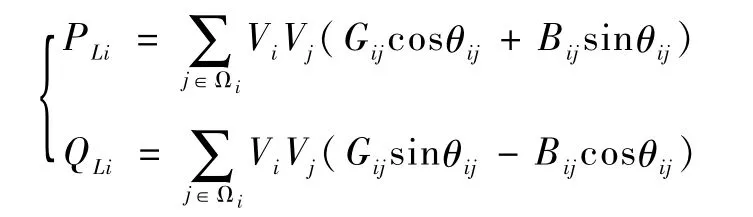
因此,将负荷预测值作为一类特殊量测,有量测方程zs=hs(x,S),如下式所示:
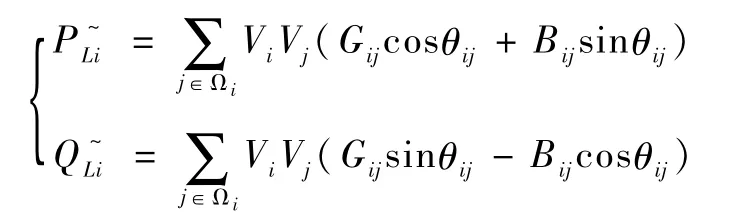
式中,上角标~用于区分量测量和状态量,下同。
SCADA系统可以提供的量测数据有:节点电压幅值Vi、支路有功功率Pij,支路无功功率Qij,节点注入有功功率Pi和节点注入无功功率Qi。设流入节点为正,流出为负。SCADA量测方程为:

式中,v表示量测误差,下角标表示量测类型。vscada表示SCADA量测误差向量。函数hscada(x,S)表达式如下:
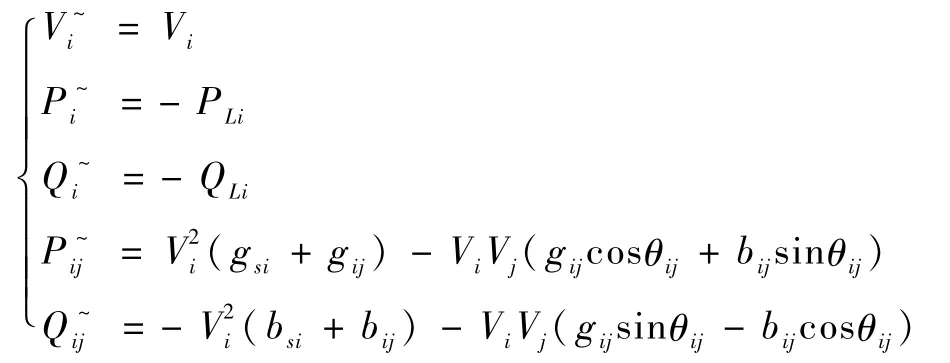
其中,i,j表示节点标号,θij表示节点i,j之间电压相角差,gij和bij分别是节点i和j之间的电导和电纳,gsi和bsi分别是此支路上节点i的对地电导和对地电纳。
PMU量测系统可以测量节点电压幅值和相角,与该节点相连支路的电流相量(设流入节点为正)。根据基尔霍夫电流定律,令流入节点的电流为正,Ii,Re和Ii,Im分别表示节点注入电流Ii的实部和虚部,Iij,Re和Iij,Im分别表示支路电流Iij的实部和虚部。PMU量测方程为:

式中,vpmu表示PMU量测误差向量。函数hpmu(x)表达式如下:
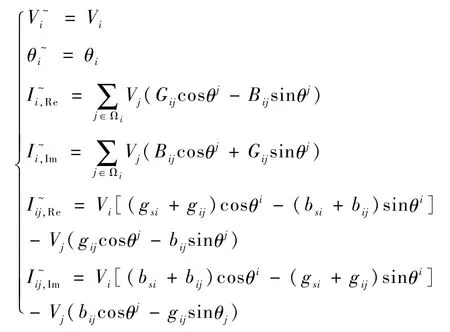
式中,Ωi表示配电网中与节点i相连的节点集合,Gij,Bij分别表示节点导纳矩阵中(i,j)项元素的实部和虚部。
综上所述,本文考虑的量测模型为混合量测模型,量测方程由SCADA量测方程、PMU量测方程和等式约束关系组成,即:
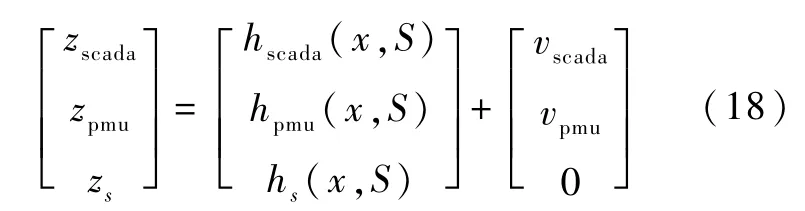
3.2 基于动态负荷预测的CKF算法流程图

图1 基于动态负荷预测的CKF算法流程图
4 算例分析
基于所提模型和算法,采用MATLAB编写了仿真程序,用IEEE119节点配电系统数据对所提方法有效性进行验证。为保证状态估计可观测性,在算例系统中采用的量测配置方案如下:随机设置30%的节点(36个)布置PMU量测,40%的节点(47个)布置SCADA量测,其余节点以伪量测补足。PMU电压幅值量测标准差取0.002 pu,电压相角量测标准差取0.05°。定义电流相量量测误差:分别表示电流相量真实值和量测值。电流相量量测标准差取0.001 pu;SCADA电压量测标准差取0.01 pu,功率量测误差标准差取0.001 pu。伪量测数据类型和SCADA量测相同,精度较低,量测误差标准差为SCADA同类型量测3倍。设置三组实验:分别使用扩展卡尔曼滤波算法、容积卡尔曼滤波算法、基于动态负荷预测的容积卡尔曼滤波算法进行动态状态估计。为模拟配电网运行状况,令节点负荷按某地区日负荷曲线变化,通过潮流计算获得状态真值。设置动态状态估计平启动,即状态初值设置如下:各节点电压幅值初值为1pu,电压相角初值为0°,节点负荷初值为0 pu。设一日内每1 min做一次动态状态估计,计算1440次,统计状态估计结果。
随机选取节点81,比较改进后的CKF算法与标准CKF算法估计性能差别,图2和图3分别为1440次动态状态估计中节点81电压幅值和电压相角估计结果。

图2 节点81电压幅值状态估计结果

图3 节点81电压相角状态估计结果
由图2和图3可见,DLP-CKF动态状态估计算法在平启动的情况下,负荷预测难以跟随系统状态变化。但是随着估计次数的增加,基于负荷预测的状态预测效果逐渐显现,与标准CKF算法相比,在负荷发生波动时仍能保持很好的状态追踪效果,电压幅值估计准确度提升明显。

式中:Vk与θk分别为k时刻电压幅值与电压相角状态估计值,分别为k时刻电压幅值与电压相角的状态真值。随机取稳定后某状态估计点分别计算上述性能指标,统计、整理实验数据如表1所示。
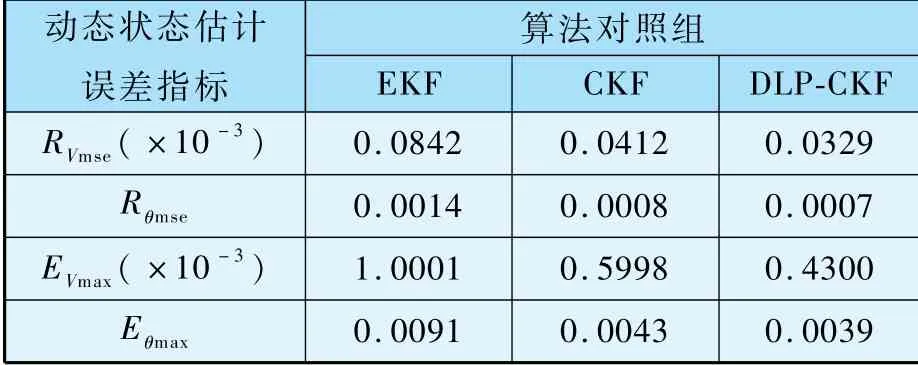
表1 不同动态状态估计算法估计误差比较
由表中数据可见,基于容积卡尔曼滤波器模型的动态状态估计算法,在估计效果上明显由于传统EKF算法。在给定量测数据冗余度较高,动态状态估计整体精度较高时,EKF在计算雅可比矩阵时引入的线性化误差突显出来。三种算法中,DLP-CKF算法表现出相对最优的估计性能。相比标准CKF算法,该算法提供了更有效的状态预测手段,因此提高了状态估计精度。
5 结 论
本文为改进电力系统动态状态估计算法状态预测环节,引入动态负荷预测模型预测电力系统运行状况,对节点负荷做两参数指数平滑预测;再将预测负荷量作为特殊量测,通过在量测方程中添加等式关系约束状态量;从而代替传统动态状态估计直接对状态量做线性外推的预测方法。在容积卡尔曼滤波算法框架下,文中给出状态误差协方差矩阵在状态转移过程中的计算公式,提出基于动态负荷预测的配电网CKF动态状态估计算法。最后在IEEE119节点系统上进行仿真分析,证明算法有效性。
仿真结果表明,基于动态负荷预测的CKF动态状态估计算法相比标准CKF算法计算精度有所提高。本文所提算法在负荷预测步选用两参数指数平滑预测模型,预测准确度相对较低,选用更精确的配电网负荷预测算法有利于进一步提高状态估计精度。
