数形结合思想在初中数学教学中的渗透
2021-09-15赵宏奎

摘要:随着新一轮基础教育的不断改革,对当前的数学教学作出了更新、更高的要求,因此,教师要探索在教学中自然融入数学思想的路径,让学生在掌握数学知识、技能的同时感知、理解并运用数学思想,最终促进学生的综合性发展。
关键词:数形结合思想;初中数学教学;渗透
目前,在数学教学中仍存有一些问题,比如部分教师“以知识教育为主”的陈旧思想不仅会磨灭初中生对数学课的热情,甚至还会抑制初中生数学素养的稳步提升。因此,为了扭转这种局面,教师必须将数形结合思想融入到数学学习实践中去,使初中生能够加以运用。笔者结合初中生数学思维发展的总体特征,在本文提出了以下三点数形结合思想在初中数学教学中的渗透策略,希望可以为其他教师提供有效的借鉴和参考。
一、“以形代数”,渗透数形结合思想
初中阶段的数学教学包含一些比较复杂的数量关系,而该阶段学生的抽象思维水平还有待进一步提升,在学习这些数量关系时难免会遇到各种各样的问题或困惑,对此,教师就需要展开针对性的指导,那么在指导的过程中就可以通过“以形代数”的形式来帮助学生直观地掌握“数”和“形”二者之间的关系,并引导学生善于利用“形”来代替“数”,这样一来就可以让学生实现从具象到抽象的顺利过渡,有效实现对数形结合思想的渗透。
例如,在教学“勾股定理”时,教师在课上利用投影仪展示了一张图片,内容是为了对毕达哥拉斯学派成立进行纪念而发行的邮票。
并引导学生结合图片讨论,使学生观察图形中的内容,将重点放在三个正方形上,结合与勾股定理有关的知识来分析面积之间又怎样的关系,并尝试将三个图形的数量关系用“数”表达,从而提高初中生对数形结合思想的应用意识。
二、“以数代形”,渗透数形结合思想
我们都知道利用图形可以给学生的视觉带去较强的冲击,将课本中过于复杂的数量关系以一种更直观的形式呈现给学生,有助于学生把握数学学习的规律。要想提高初中生分析、解题的整体效率,教师就要加强对数形结合思想的渗透,通过“以数代形”的方式来把某些图形问题逐步转化为简单的数量问题,在此过程中可以组织学生结合“数”的逻辑性特点,对图形加以补充,在一定程度上可以弥补初中生观察图形时的缺陷,从而使其更高效、快速地解决问题。
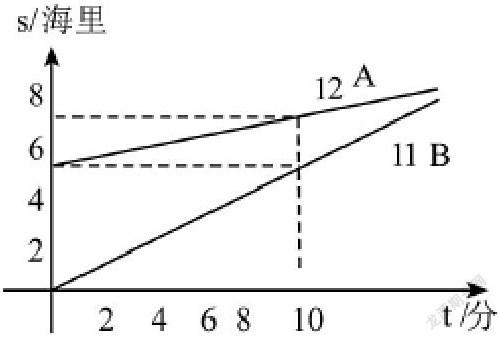
例如,教师向学生出示了这样一个问题:请看下图,图中11,12相对于目的地的距离,与追赶时间分别表示B,A两船t之间的关系。同学们想一下,t是多少时,B船才能追赶上A船?并利用多媒体给学生呈现了图形。
如果单靠图形的观察学生是无法得出最终结果的,此时,教师引导学生结合大屏幕上的图形来列出11和12的“函数表达式”,并将两个表达式结合为方程组,通过求解来获得答案,在此过程中有利于让学生探寻到“数”和“形”之间的关系。
三、“数形互换”,滲透数形结合思想
除了利用上述两种“以形代数”和“以数代形”方式来帮助学生解决问题以外,教师还要引导学生进行“数形互换”,以此来帮助学生更好地阐述“数”和“形”之间的具体关系,在教师的层层引导之下逐步把握数学学习的规律,最终凭借自己的大脑思维来分析、解决问题。因此,教师要指导学生加强对“数形互换”的运用,进一步启发初中生的数学思维,是他们真正地理解、内化数学思想。
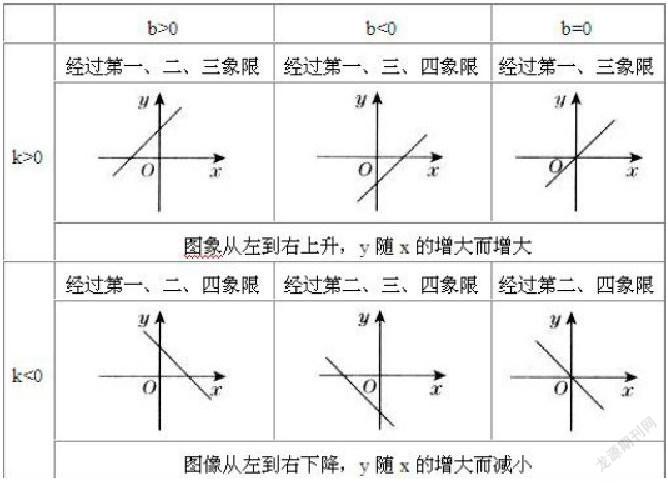
例如,在教学“一次函数”时,为了让学生能够掌握一次函数y=kx+b中常数k的值与图像的相互对应关系,教师就运用了“数形互换”的方法,向学生呈现了下表。
教师引导学生根据图形来理解表格中的内容,巧妙地渗透了数形结合的思想,这样可以使学生深刻的了解一次函数的变化规律,让学生体会到数形结合的价值。
综上所述,数学教师要遵循先进的教学理念,不断探索并创新融入数形结合思想的形式和方法,充分地结合本班学生的实际情况、生活经验以及数学基础来开展教学活动,通过恰当的引导帮助学生发现并掌握“数”和“形”之间的关联,并尝试对二者进行灵活地转换和应用,从而才能使学生运用数学思想来解决一系列问题,让学生在习得知识的同时获得数学学科的关键技能、掌握数学课程的重要思想,最终取得综合性的发展,从而才能更好地适应社会的发展。
参考文献:
[1]任岩.初中数学教学中数形结合思想的应用探究[J].发明与创新(职业教育),2021(07):140+143.
[2]刘宜东.如何在初中数学教学中巧用数形结合思想[J].数学大世界(上旬),2021(06):92.
新疆第八师石河子148团中学 赵宏奎
