核心素养视角下函数概念教学再思考

谷晓凯

摘  要：函数概念课的教学要注重设置自然的问题，通过问题引导学生经历概念的形成过程，以培育学生的数学抽象素养. 在教学中，教师既应该注重数学史的引入，以激发学生的学习兴趣;又应该注意精心设置课堂引入和课堂小结两个环节，以引领学生认识数学的价值，引发学生的学习动机.

关键词：核心素养;函数概念;数学抽象

函数是中学数学的核心内容，作为刻画现实世界中变化规律的重要数学模型，函数标志着常量数学向变量数学的过渡. 同时，函数内容也是培育学生数学抽象素养的良好素材. 更重要的，对函数概念的学习可以引导学生学会用数学眼光观察世界，用数学思维思考世界，用数学语言表达世界，从而帮助学生了解数学的价值，提高学习数学的兴趣. 下面结合人教版《义务教育教科书·数学》八年级下册（以下统称“人教版教材”）“19.1.1 变量与函数”一课，以核心素养的视角，从培育学生数学抽象素养，以及发展学生情感、态度、价值观的角度谈谈对本部分内容的教学思考.

一、为什么要学习函数概念

函数是中学数学中重要的基本概念之一. 但教学实践表明，学生在解决与函数有关的问题时并不使用函数的概念. 那么，为什么还要学习函数的概念呢？事实上，函数概念的出现既是客观现实的需要，又是数学内部发展的需要. 一方面，现实世界是不断运动变化的，这些变化中蕴含着各种各样的客观规律，用数学的方法探索这些规律是函数研究的主要内容;另一方面，函数概念是学生学习变量数学的起点，用函数作为纽带可以把代数式、方程（组）、不等式等知识有机地联系起来. 人教版教材在本章的引言部分正是从这两个方面引导学生体会学习函数的必要性的. 因此，作为函数教学的起始课，教师应该从章引言开始，侧重引导学生理解学习函数是研究客观现实的需要，从而让学生会用数学眼光观察世界.

基于此，针对本节课的“课堂引入”环节做如下教学设计.

问题1：同学们知道“坐地日行八万里，巡天遥看一千河”这句诗的意思吗？

教师引导：诗人用文学的眼光看地球的运动，其非凡的想象力表现出了强烈的浪漫主义情怀. 实际上，从宇宙中的星球到周围的事物，包括我们肉眼看不到的微观世界，存在着大量运动变化的现象，可谓“万物皆变”.

追问：你能再列举一些运动变化的例子吗？

预设：学生举例，教师从运动变化的角度予以点评.

教师引导：关于这些运动变化的现象，物理课上我们学习过：物体的静止是相对的，而物体的运动是绝对的. 那么，如何运用数学知识看待这些现象呢？这节课，我们就用数学眼光、数学方法去认识和研究这些运动变化的现象.

【设计意图】上述设计从“文学眼光”到“物理眼光”，再自然过渡到“数学眼光”，在比较中培养学生从不同角度（特别是数学角度）看问题的意识，并初步领悟引入函数概念的必要性. 同时，学生能体会到数学与生活之间、数学与其他学科之间的联系，并通过这种联系认识数学的价值，进一步激发学生学习函数的兴趣.

二、让函数概念自然形成

有研究表明，函数是学生数学学习中感到最困难的概念之一，部分学生到九年级仍然不能正确理解什么是函数. 造成这一结果的原因除了学生已有的认知结构中缺乏与变量数学相联系的知识之外，更与函数概念本身的高度抽象性及初中学生抽象思维能力不足有关. 因此，函数概念的教学一定要体现概念的形成过程. 教师应该设置合适的问题，引导学生经历由实际问题到函数概念的抽象概括过程. 同时，要留给学生充分的时间进行独立思考、合作交流等自主活动. 其中，设置合适的问题是教学的关键. 教师要从学生的认知规律出发设置合理的、富有启发性的、自然的问题，这样才能促使学生主动认知并建构函数概念，从而让学生体会到函数概念是通过自己的建构自然形成的.

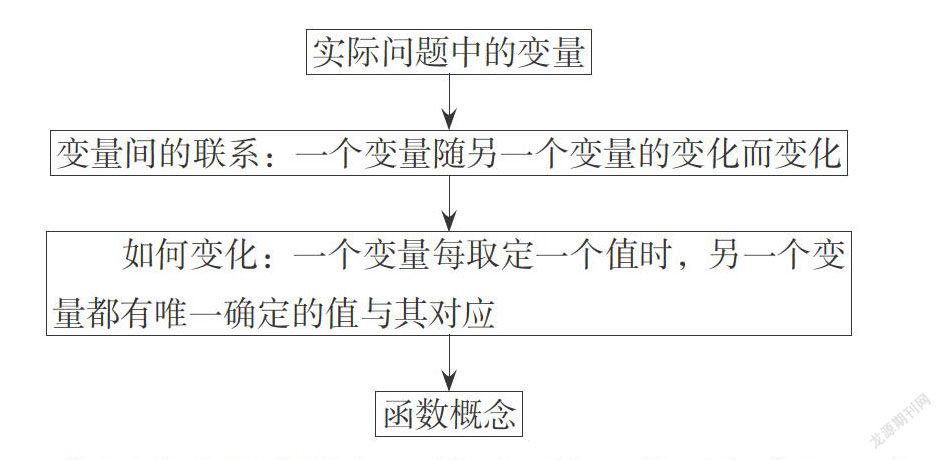
人教版教材中关于函数概念部分的编排非常有利于学生理解函数概念是如何自然形成的. 首先，人教版教材提供了如下四个与生活实际紧密联系的问题：（1）汽车行驶路程与时间的关系;（2）电影院票房收入与售票张数的关系;（3）水中涟漪（圆的面积与半径的关系）;（4）用固定长度的绳子围出矩形（矩形邻边关系）. 通过对这四个问题的分析得出变量与常量的概念;接着，又针对这四个问题设置了一个“思考”，引导学生归纳得出结论——上述每个问题中的两个变量都相互联系，当其中一个变量取定一个值时，另一个变量就有唯一确定的值与其对应;最后，通过问题（5）“心电图（生物电流与时间关系）”和问题（6）“我国人口数统计表（人口数与年份关系）”，结合前面歸纳出的结论概括出函数的概念. 其中，函数概念自然形成的思考路径如下图所示.

[实际问题中的变量][变量间的联系：一个变量随另一个变量的变化而变化][    如何变化：一个变量每取定一个值时，另一个变量都有唯一确定的值与其对应][函数概念]

按照这个思考路径，针对“给函数下定义”环节可做如下教学设计.

问题2：问题（1） ～ （4）中都有哪些量？从运动变化的角度看，它们有哪些共同特点？

预设：学生在认真观察、比较、思考的基础上归纳得出变量和常量的概念.

追问1：同一个问题中的两个变量之间有什么联系？

预设：一个变量随另一个变量的变化而变化.

追问2：具体是怎么变化的？

预设：在一个变化过程中，一个变量每取定一个值时，另一个变量都有唯一确定的值与其对应.

【设计意图】问题2意在引导学生从全新的角度（运动变化的角度）认识熟悉的问题情境. 这里，“熟悉的问题情境”有利于学生联系已有的经验，而丰富的经验背景是概念形成的前提. 因为有基于章引言的课堂引入做铺垫，所以从“全新的角度”理解概念的形成就显得非常自然. 更重要的是，这种建立在“旧”的基础上的“新”，能引起学生的好奇，从而引发学生的学习动机. 追问1和追问2引导学生聚焦问题中的变量，并使学生通过层层深入的思考初步理解函数概念的本质.

对追问2的预设，学生可能很难达到，这就需要教师适时引导，让学生回到问题（1） ～ （4），通过对问题中的变量进行赋值来研究变量之间的变化关系. 需要注意的是，教师不应该拘泥于学生能否用准确的数学语言描述这种变化，而要关注学生是否感悟到了变量之间的这种对应关系.

问题3：问题（5）（6）中的两个变量之间也有前面所述的关系吗？试举例说明.

预设：学生利用图表举例说明变量之间的单值对应关系.

【设计意图】问题3提供了两个概念性变式素材，既能让学生进一步理解变量之间的单值对应关系，又为后面学习函数的多种表示方法做准备. 让学生举例说明意在引导学生关注对函数概念本质的理解.

问题4：上述问题中两个变量之间的关系就是我们要学习的函数. 你能给函数下个定义吗？先独立思考，再与同伴交流.

预设：师生归纳总结出函数的概念.

【设计意图】问题4意在引导学生用数学语言表述函数概念. 要求学生在小组交流之前先独立思考，意在培养学生良好的学习习惯.

虽然教学实践表明，学生很难用规范的数学语言独立表述出函数的概念. 但在不断的思考、交流的过程中，学生会逐渐进入“愤悱”的状态，想用规范、准确的数学语言表述函数概念的欲望会越来越强烈. 此时，教师再给出函数的定义，学生会感受到数学语言的严谨之美. 同时，学生“会用数学语言表达世界”的素养也得到了提升.

三、“函数简史”助力教学

罗增儒教授认为，指向素养教学的数学课堂应该努力渗透数学史、数学家、数学精神和数学应用等数学文化要素. 英国数学史家福韦尔总结了数学教学中运用数学史的各种理由，其中包括：激发学生的学习动机;改变学生的数学观;保持对数学的兴趣;让学生知道并非只有他们有困难，因而获得心理安慰;培养优等生的思维宽度和深度;等等. 可见，在课堂教学中引入数学史有助于学生了解数学的价值，提高学生学习数学的兴趣，增强学好数学的信心. 因此，把数学史融入课堂教学是培养学生数学学科核心素养的有效策略.

函数概念从产生到初步完善历经数世纪之久，期间有许多史料可对教学产生借鉴. 结合初中生的知识储备和心理特征，教师可以在教学中设置如下“函数简史”环节，选择函数概念发展中的关键节点介绍给学生.

1638年，意大利天文学家、物理学家、数学家伽利略在《关于两门新科学的对话》一书中，研究了变量之间的关系，这标志着函数概念的萌芽;1673年，德国哲学家、数学家莱布尼茨在他的一篇手稿里首次使用“函数（function）”一词来表示任何一个随曲线上点的运动而变化的量;1718年，莱布尼茨的学生、瑞士数学家伯努利在给函数下定义时特别强调，函数要用公式来表示.

之后，瑞士数学家欧拉于1748年将函数明确定义为解析式，但很快又对函数的定义进行了修正，将函数看作“具有依赖关系的变量”. 一直到1837年，德国数学家狄利克雷对欧拉的定义进行了修正，给出了更接近現行教材中的函数定义.

在我国，清朝数学家李善兰把“function”译成“函数”，提出“凡式中含天，为天之函数”.

虽然经过几百年的锤炼和变革，才形成了函数概念的现代定义，但这并不意味着函数概念发展的历史终结，它还有更广阔的空间等着同学们去探索.

【设计意图】通过以上史料，学生能了解教材中函数概念的由来及曲折的发展历程，从而激发学习函数的动机，获得学习函数的心理安慰，增强学好函数的信心，进而更好地认识数学学科的发展. 同时，学生熟悉的伽利略等数学家的多重身份能让学生进一步体会到数学与其他学科之间的联系. 总之，这些史料使函数概念在学生面前变得立体丰满，能够有效拉近学生与函数概念之间的距离，激发他们学习数学的兴趣.

四、“小结”不能“结”

众所周知，数学教学应追求前后一致、逻辑连贯、注重整体. 教师应把每堂课教学的知识置于整体的知识体系中，注重知识的结构和体系，引导学生感受数学的整体性. 课堂小结在这些方面应发挥更重要的作用. 在课堂小结环节，教师不能仅仅通过引导学生对本节课的知识和方法进行梳理而为课堂教学画上“句号”，而应该通过引导学生感受本节课的知识与整体知识的关系而为课堂教学画一个“逗号”;不能仅仅满足于通过解决本节课产生的问题而为课堂教学画上“句号”，更应通过引导学生发现并提出更多的问题而为课堂教学画上“问号”. 总之，“小结”不能“结”，要留有余味，留给学生进一步思考的空间.

基于以上观点，针对本节课的“课堂小结”环节可做如下的问题设计.

问题5：本节课，我们学习了哪些内容？

预设：函数的概念.

追问1：你能举例说明什么是函数吗？

追问2：我们是怎样得到函数概念的？

【设计意图】通过追问1引导学生关注函数概念的本质，淡化概念的形式化表达. 追问2意在引导学生关注函数概念的形成过程，从中进一步感悟数学抽象的基本思想.

问题6：关于函数，你还有什么问题吗？

【设计意图】通过学生对问题6的解答，结合学生的课堂生成，教师可适当介绍函数的后续学习内容（具体函数、表示、性质、应用等），使学生能初窥函数知识体系的全貌，激发他们继续学习的欲望.

五、进一步思考

笔者在参阅大量研究函数概念教学的文章后，发现研究者大多聚焦于六大数学学科核心素养中数学抽象、数学建模等的培育，很少有研究者讨论怎样通过函数概念的教学培养学生学习数学的兴趣，而提高学生学习数学的兴趣是核心素养中情感、态度、价值观部分的要求，也是数学必备品格的重要组成要素.

在按上述设计进行的课堂教学实践中，通过课堂观察发现，学生对“课堂引入”“函数简史”“课堂小结”三个环节表现出了浓厚的兴趣. 通过课后访谈发现，部分优等生对“给函数下定义”这个环节印象深刻. 究其原因，这应该与核心素养视角下函数概念教学的重新设计有关. 上述教学设计中，教师对知识和能力的教学注重用自然的、富有启发性的问题引导学生积极思考，从中获得数学思维的乐趣;通过比较用不同“眼光”看待同一问题，引领学生认识数学的价值;通过函数简史的引入，丰富函数概念的文化意蕴，使学生从中感受到数学的魅力，从而提升学习数学的兴趣. 在“课堂小结”环节，学生通过初识函数知识的整体架构而产生强烈的学习兴趣和求知欲. 因此，核心素养引领下的数学课堂教学，在关注知识和能力教学的基础上，也应注重发展学生的情感、态度和价值观，以培养学生的数学兴趣，兴趣是发展学生核心素养的必要条件.

参考文献：

[1]史宁中. 高中数学课程标准修订中的关键问题[J]. 数学教育学报，2018，27（1）：8-10.

[2]李海东. 基于发展学生核心素养的初中数学教学[J]. 中国数学教育（初中版），2019（4）：3-8，13.

[3]中华人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[4]汪晓勤. HPM：数学史与数学教育[M]. 北京：科学出版社，2017.

[5]喻平. 数学核心素养评价的一个框架[J]. 数学教育学报，2017，26（2）：19-23.

[6]罗增儒. 指向素养教学的课堂研修[J]. 中学数学教学参考（中旬），2018（7）：11-22.

[7]祖丹，孔凡哲. 数学必备品格的组成要素分析：基于数学家的视角[J]. 天津师范大学学报（基础教育版），2020，21（2）：59-65.