观念统领建构联系感悟思想

张晔

大观念统整的单元整体教学突破常见的教学内容逻辑，按照知识体系的建构顺序展开，学生在学习所有知识点后再解决综合性问题。这样的教学以驱动性大问题的解决过程为线索组织教学结构，为基础性、结构性的教学内容与生发性教学内容的紧密结合提供可能。

一、统整教学内容，让知识结构化

大观念统整的单元整体教学要发挥“结构”与“联系”的作用，将知识有机地结合起来，帮助学生领悟知识背后蕴含的数学思想方法，并将其迁移应用于新情境中，以促进他们的意义理解和自主迁移。

三角形面积公式的推导和梯形面积公式的推导都可以用“倍拼”和“割补”的方式进行转化，将这两个内容整合在一起学习，有利于学生感悟两种图形面积转化过程的内在联系，凸显转化思想，并使探索材料的利用更加充分。教学中，笔者将“三角形和梯形的面积”第1课时目标定为：经历三角形和梯形面积的探究活动，体验“倍拼”转化方法的应用，感受三角形和梯形面积转化中的通理通法;掌握三角形和梯形面积计算公式，并能正确计算。第2课时（“还有别的推导方法吗？”）目标定为：用多种“割补”方法推导三角形和梯形面积公式，积累面积公式推导经验，感悟数学文化。

“倍拼法”属于非等积转化，要求学生面对一个图形的问题，想到虚构另一个与之全等的图形，不仅要达到二者合拼成规则图形的目的，还要方便计算时“消去”这个增加的图形面积，这是对学生空间观念的新挑战。由此，笔者团队设计了本单元的开启课——《数面积》，让学生主动运用“割补法”“倍拼法”将未知图形转化成已知图形，进一步体验“数方格”在探究图形面积中的应用。“倍拼法”的难点不在于操作，而在于“怎么想到的”，这是面积公式推导的落脚点。基于此，笔者没有让学生动手去拼，而是要求学生思考后把想法画在方格纸上，利用数形结合思想推导面积计算公式。在图形转化后，笔者首先引导学生理解转化后形成的平行四边形面积是三角形的两倍;其次引导学生进行公式的演绎推理，将平行四边形面积公式中的元素替换成与之对应的三角形中的元素，从而得到三角形的面积计算公式。整个过程就是一种“等量代换”。

以上推导图形面积公式的数学活动经验需要在“做”中积淀，它是一个逐步积累的过程，是被逐步启发、优化的。在推导平行四边形面积公式时，笔者给学生提供了“转化—找联系—推导公式”的基本思路，帮助学生理解和迁移知识。在探究三角形面积公式时，笔者提供方格背景，在其上刻画出三角形的量性特征，使学生在研究中有具体的数量可以把握，降低抽象性。学生经历“倍拼法”转化及推导三角形面积公式的过程，有利于后续自主探究得出梯形面积公式。再次探究三角形和梯形面积时，笔者提供方格背景，让隐藏的高线与中位线显性化，从而降低操作与验证的难度。学生有上一节课的学习经验，不仅能用“倍拼法”，还能用“以盈补虚”的方法进行转化，从而推导出三角形和梯形面积公式，学生又一次经历了转化及推导公式的过程，积累了基本活动经验。

二、统整数学方法，让思维有深度

《多边形的面积》这个单元有一个建构知识内在联系的点——梯形面积公式。在拓展课上，教师将梯形面积公式与其他图形面积公式的推导有机整合，可以强化学生对公式之间关联的理解，使学生明晰“通用公式”的通性，感受数学的魅力。

笔者设计了两个教学环节：一是重构梯形面积公式与其他图形面积公式之间的联系，二是在拓展练习中促进学生思维走向深刻。课上，笔者首先出示等底等高、形状不同的三个梯形（如下图），引导学生通过观察发现这些梯形的面积相等。

接着，笔者引导学生思考像这样面积相等的梯形能画出多少个，学生合作探究发现这样的梯形有无数个。然后，笔者展示学生补画的梯形，遮盖该梯形的上底并提问：如果下底是4.5厘米，上底是多少？从而得出：求梯形的一条底，必须得把上底和下底看成一个整体。以此为引，笔者提出“上底最小可以是多少？这是一个怎样的图形”的问题。在学生想象出是无限接近三角形的图形时，笔者用几何画板演示上底长度变为0，梯形变成了三角形的过程。此时学生发现三角形（即上底为0的梯形）面积公式S=（a+b）h÷2=（a+0）h÷2=ah÷2。最后，笔者又通过几何画板演示上底等于下底时，梯形变成了平行四边形，并引导学生探究得出：当a=b时，平行四边形的面积S=2ah÷2=ah。同理，如果是直角梯形，还可以推算出长方形的面积公式。

以上教学，教师用几何画板分别演示将梯形变成三角形、平行四边形、长方形、正方形的过程，引导学生经历了梯形面积公式与其他4种图形面积公式的转化过程，理解了梯形面积公式是其他4种图形面积的“通用公式”。这样的重构与整合，使学生的头脑中构建出一幅知识网络图，促进了学生几何直观的发展。

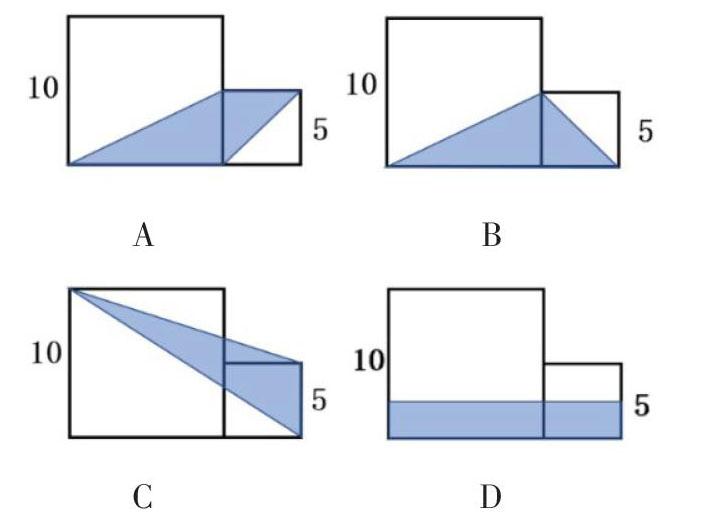
在拓展环节，笔者出示S=（10+5）×5÷2，提问学生：看到这个算式，你想到了哪些图形？下面4个组合图形（如下图）的面积，哪些可以用这个算式表示。

学生独立思考后讨论、交流得出：A、B都可以利用公式计算得出;C是一个钝角三角形，面积是5×（10+5）÷2;D是一个长方形，面积是（10+5）×（5÷2），4个都符合题目要求。这样设计的目的是引导学生“以式想形”，多向沟通图形之间的联系，促进学生空间观念和发散思维的发展。

三、统整数学文化，让认知更丰富

筆者通过深入挖掘《多边形的面积》这一单元蕴含的数学文化资源，建构学习线索，找到合适的切入点，将数学文化学习与探求新知融合，组织学生进行数学探究活动。以魏晋时期数学家刘徽发展并系统化了的重要方法——“出入相补”作为文化主线一以贯之，让大单元整体教学承载更多的教育价值。

笔者借助“出入相补”这一核心问题的探究，以不同的方式将数学文化嵌入各个课时的学习中。在《平行四边形的面积》总结环节，笔者引导学生回顾“转化—找出关系—推导公式”的学习过程，将“青朱出入图”以微课形式呈现，向学生介绍“出入相补”原理，重在使学生初步体验转化的方法。在学习“三角形和梯形的面积”时，学生先后经历“倍拼法”和“割补法”的探究过程，笔者适时引入“出入相补”，并向学生介绍《九章算术注》中有关邪田和箕田的面积公式推导方法，重在对转化方法的拓展。这样做既深化了学生对转化思想的理解，又传承了数学文化。

（作者单位：黄石市广场路英才学校）

责任编辑  刘佳