基于Shapley值抽样估计法的风-光-水互补发电增益分配方法
2021-09-14张丽琴张秋艳符登辉
张丽琴,谢 俊,张秋艳,符登辉
(河海大学 能源与电气学院,江苏 南京 211100)
0 引言
可再生能源发电是满足可持续性、可靠性和经济性要求的重要发电方式之一[1]。我国的风能、太阳能和水能资源丰富,且具有天然的互补特性,风电、光电和水电的多能互补、协同发电调度已成为研究热点[2-3]。针对风、光资源随机性强的特点,如何利用风、光、水自然资源的天然互补特性,实现多电站联合运行的规模效益,发挥梯级水电的调节作用,平抑风电、光电的波动,提高风电、光电的消纳水平,是发展风-光-水互补发电亟需解决的问题之一。
针对风电和光电随机性强的特点,文献[4]通过风电/光电的预测出力均值、标准差描述风电/光电的出力不确定性;文献[5]通过场景模拟得到的风电期望出力、预测误差标准差来描述风电出力的不确定性。上述研究均假定风电场/光伏电站在各时段的预测误差/预测出力服从正态分布,但研究表明正态分布并非实际的风电预测出力分布[6]/风电预测误差分布[7]。针对多座风电场、光伏电站和水电站之间的互补效应,文献[8]构建β-分位函数描述日前电力市场中多座风电场组成的风力发电联盟出力,但该方法难以量化联盟中各利益主体的出力情况;文献[9]提出一种高斯混合模型来表示多座风电场出力的相关性,但处理大量风电利益主体构成的高维问题时,该模型相关参数的估计较为困难;文献[10-12]分别建立多座风电场出力相关性模型、多座光伏电站辐照度相关性模型以及多座水电站构成的梯级水电模型,但上述模型未考虑风、光、水多能互补。针对风电和光电的波动性问题,文献[12]以风电出力不足为例,以购买火电旋转备用的净社会效益最大为优化目标,通过水电优先、火电补差的方式保证了远距离水-火-风联合运行系统的稳定性和经济性;文献[13]以经济效益最大为优化目标,建立由水电机组为风电的不确定性提供备用的风-水发电系统,分析风电预测误差对系统的影响。
为激励风电、光电和水电利益主体参与互补发电,需要提出公平、有效的增益分配方法[4]。Shapley值SV(Shapley Value)法是一种常用的合作效益分配方法,目前已应用于梯级水电站发电权的分配[14]、网损和排放减少量的分配[15]、虚拟电厂和配电公司的收益分配[16]、应对风电出力不确定性的备用成本分配[17]等。然而,n个利益主体合作博弈问题共有2n-1 种联盟组合,采用SV 法时需求解2n-1 个合作博弈模型,因此,SV法的计算复杂程度随利益主体数量的增多呈指数级上升,会产生组合爆炸问题。为提高SV 法的实用性,需寻求一种新的分摊方法,该方法既需继承SV 法的优良特性,又需克服SV 法在解决较多利益主体增益分配问题时的组合爆炸问题。
抽样方法已用于解决一些经典的合作博弈的组合爆炸问题[18],Shapley 值抽样估计SSVE(Samplingbased Shapley Value Estimation)法从同质的子群体中进行抽样,实现了抽样结果的精确性[19]。但在分层抽样的过程中,样本量分配方法会直接影响估计结果。寻求能在精确度和计算复杂度等方面达到平衡的最佳样本量分配方法,是保证SSVE 法得到更精确的Shapley 估计值以及应用于含大量利益主体的风-光-水互补发电系统增益分配问题的关键。
为量化风-光-水互补发电增益,针对风-光-水互补发电的特点,本文提出考虑发电资源随机性、波动性和互补效益的风-光-水互补发电系统优化调度模型;为激励多利益主体参与互补发电优化调度,并克服经典SV 法的组合爆炸问题,本文提出基于SSVE 法的风-光-水互补发电增益分配方法,分析4种不同的样本量分配方法对估计精确度和计算复杂度的影响;采用云南省某区域4 个利益主体风-光-水互补发电算例分析SV 法和SSVE 法的特点,采用雅砻江清洁能源基地37 个利益主体风-光-水互补发电算例验证SSVE法的有效性。
1 风-光-水互补发电增益
1.1 互补发电增益的量化
多利益主体互补发电联盟S(S⊆{CWD,CPV,CHY},CWD、CPV和CHY分别为风电、光电和水电利益主体构成的集合)的增益可视为该联盟的联合优化调度发电量相较于独立优化调度发电量的超出值:
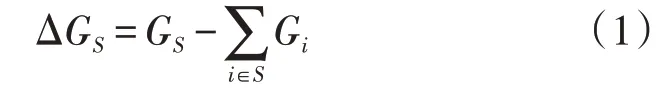
式中:ΔGS为互补发电联盟S的增益;GS为联盟S的联合优化调度发电量;Gi(i∈S)为联盟S中任意利益主体i的独立优化调度发电量。
1.2 风-光-水互补优化调度模型
联合优化调度发电量指经互补优化调度后互补发电联盟S的最大发电量,即:
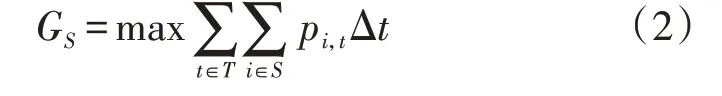
式中:pi,t为利益主体i在t时段的最优出力,是决策变量;T为调度时间;Δt为每段调度时段时长。
利益主体i的独立优化调度发电量指该利益主体独立调度时的最大发电量,即:
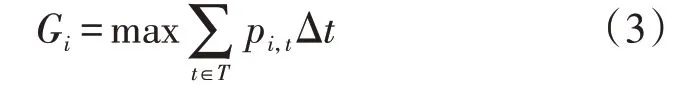
风-光-水互补发电系统在联合优化调度模式下的目标函数式(2)和在独立优化调度模式下的目标函数式(3)都应满足如下约束条件。
1)风电/光电利益主体出力约束(i∈CWD/i∈CPV)。
由于地理上邻近的风力发电资源、太阳能发电资源具有互补效益,获取考虑互补效益的风电/光电利益主体的可能出力范围的具体步骤如下。式中:Φ-1(⋅)为标准高斯分布的逆累积分布函数;Φk(⋅)为考虑k个利益主体出力相关性的k维高斯分布函数。



(6)为了进一步提高互补优化调度模型的可行性和经济性,需要忽略一些出现概率极低的可能出力,缩小最优出力范围,即:


3)系统旋转备用约束。
风-光-水互补发电系统应具备一定的旋转备用容量以应对风电出力随机性、光电出力随机性、水电机组故障等情况。

2 SSVE法
2.1 SV的计算
根据SV 法,利益主体i分配到的互补发电增益为该利益主体给所有合作联盟带来边际增益的加权值φi,即:

将所有联盟按照联盟中所包含的利益主体数目进行分层,用h(h=|S|,S⊆N)表示层数。则式(21)可改写为:

2.2 样本信息与SV法分配结果的关系
SSVE 法的关键是探索局部(各层)样本信息与全局(全部)样本信息的关系。
假设估计利益主体i的SV 共需抽取M个样本量,第h层分配到个样本量,则第h层样本的平均值为:

1)随机法。将M个样本随机分配给各层,则有:

3)Neyman 法。将M个样本按各层样本标准差比例分配给各层,则有:

4)强化学习RL(Reinforcement Learning)法。基于迭代的RL 法利用各层已知的方差信息进行探索估计,主要包含以下步骤。
(1)确定样本量M。

2.3 SSVE法的最优分配结果
采用最大似然估计方法可以获得更精确的Shapley 估计值。对于所有满足独立高斯分布的样本均值Ei∈{E1,E2,…,En},可构建如下似然函数:
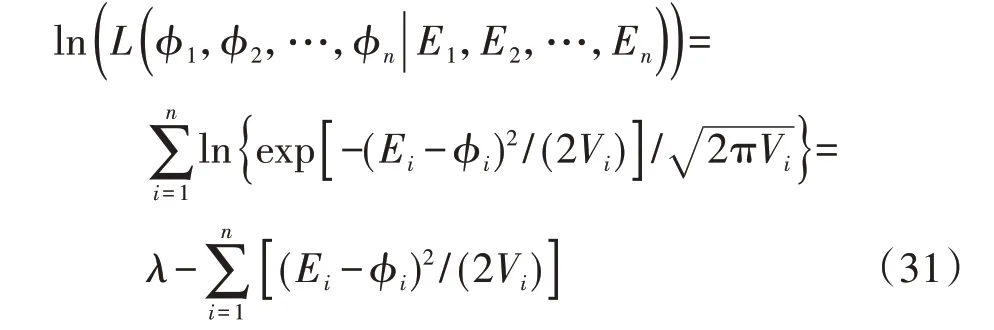
式中:L(φ1,φ2,…,φn|E1,E2,…,En)为n阶似然函数;λ为不含SV法分配结果φi的项。
由于式(31)对应的最大似然解不一定能满足全局理性要求,因此在最大似然优化问题的基础上应进一步引入全局理性约束:
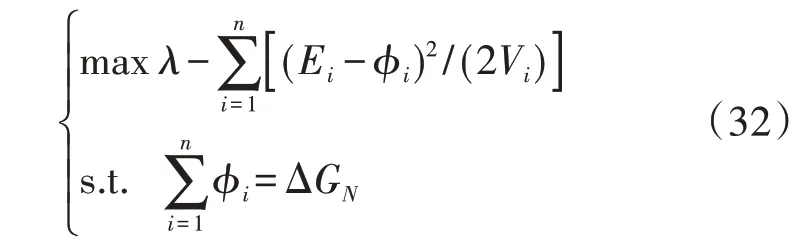
式中:ΔGN为大联盟的增益。式(32)中等式约束条件为全局理性约束[16],即要求互补发电系统的增益需全部分配给各参与利益主体。
求解上述优化问题可得到:

3 增益分配方法框架
本文提出的风-光-水互补发电增益分配方法框架如图1 所示,图中虚线与点划线箭头部分分别为SV法与SSVE法流程的不同之处。
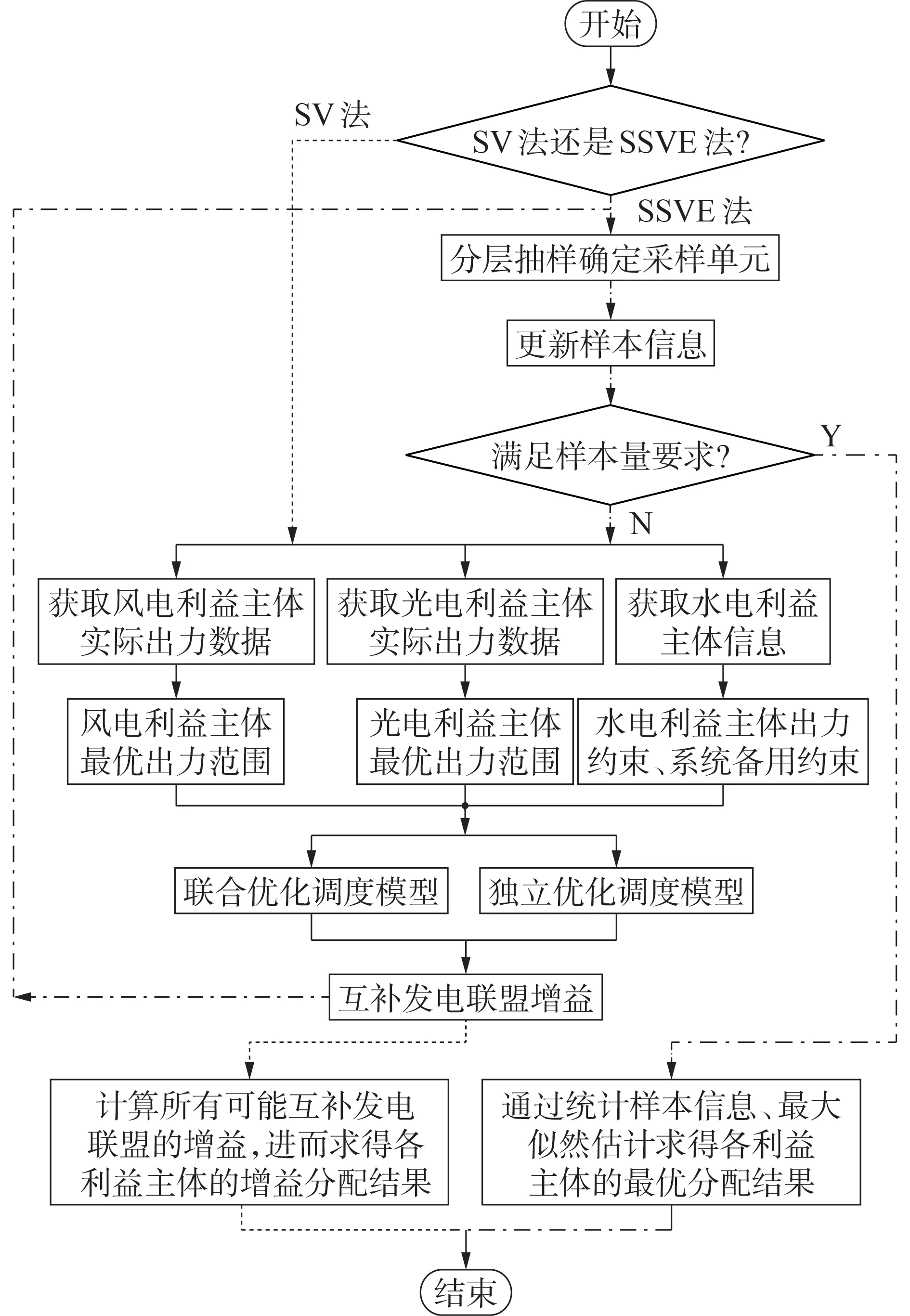
图1 增益分配方法框架Fig.1 Framework of synergistic benefit allocation method
4 算例分析
算例仿真部分均使用1.6 GHz Intel处理器、8 GB内存的计算机,通过MATLAB R2016b 软件进行仿真计算。通过2 个算例验证SSVE 法用于风-光-水互补发电增益分配问题的有效性和实用性:以4 个利益主体风-光-水互补发电算例研究样本量分配方法对SSVE 法精确性和计算效率的影响;以37 个利益主体风-光-水互补发电算例验证大量风电、光电和水电利益主体参与互补优化调度时,SSVE 法能够克服SV法的组合爆炸问题。
4.1 4个利益主体风-光-水互补发电
以风电利益主体、光电利益主体、上游水电利益主体和下游水电利益主体构成的4 个利益主体风-光-水互补发电系统为例,根据我国云南省某区域风电和光电利益主体在2019 年夏季的历史出力数据,上游和下游水电利益主体在某日的天然来水数据,建立时段时长为1 h的日互补优化调度模型,并分别采用SV法和SSVE法进行互补发电增益分配。系统参数如附录A表A1、表A2所示。
下面从精确性要求和计算效率要求出发,比较SSVE 法在采用随机法、平均法、Neyman 法和RL 法时的最优分配结果。
1)误差分布。
以SV 法分配结果为基准,计算SSVE 法采用不同样本量分配方法时的误差。以风电利益主体为例,当样本量M=900 时,SSVE 法分配结果的误差分布如图2所示。
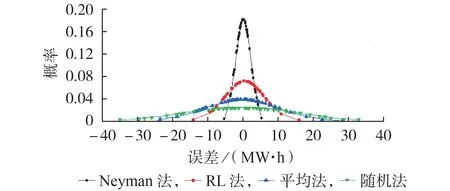
图2 SSVE法在不同样本量分配方法下的误差分布Fig.2 Error distribution of SSVE method under different sample distribution methods
从图2可以看出:4种样本量分配方法的误差均值为0,因此SSVE 法具有渐近无偏性;Neyman 法的误差分布最接近理想的误差分布,因此Neyman法的最优分配结果的精确程度最高;采用RL 法时,随着误差的增大,对应的概率急剧降低,因此RL 法也具有较高的精确程度;随机法和平均法的误差分布曲线相对平坦,当误差绝对值小于10 MW·h 时,对应的概率低于RL 法,当误差绝对值大于10 MW·h 时,对应的概率高于RL法,因此随机法和平均法的精确程度比RL法低。
2)误差率。
样本量M的大小也会影响SSVE 法下最优分配结果的误差率。以样本量M为100~900 为例对风电利益主体进行互补发电增益分配,不同样本量分配方法下SSVE 法的误差率均值如附录A 图A1 所示。由图可知,随着样本量M的增大,随机法、平均法、Neyman 法和RL 法的误差率均呈下降趋势,SSVE 法的分配结果具有渐近一致性。
以M=900 为例,进一步比较SV 法和SSVE 法的最优分配结果,如表1所示。
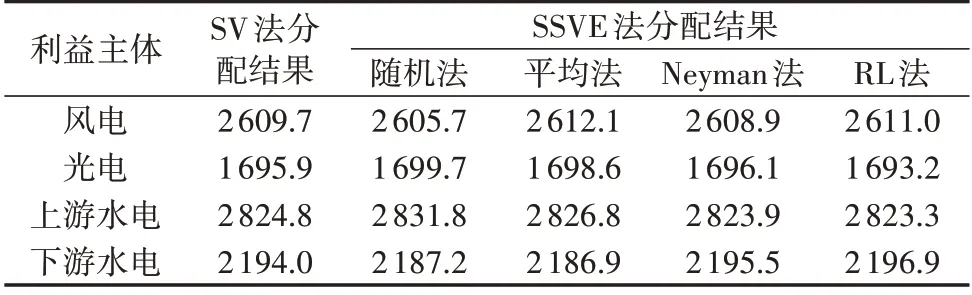
表1 最优分配结果Table 1 Optimum allocation results 单位:MW·h
由表1 可知,当样本量M=900 时,不同样本量分配方法下SSVE 法的最优分配结果的误差率均低于0.4%。
3)方差。
方差是能够反映抽样过程可靠程度的参数,下面进一步研究样本量和样本量分配方法对样本方差的影响。
随着样本量M的增大,不同样本量分配方法对应的样本方差如图3所示。
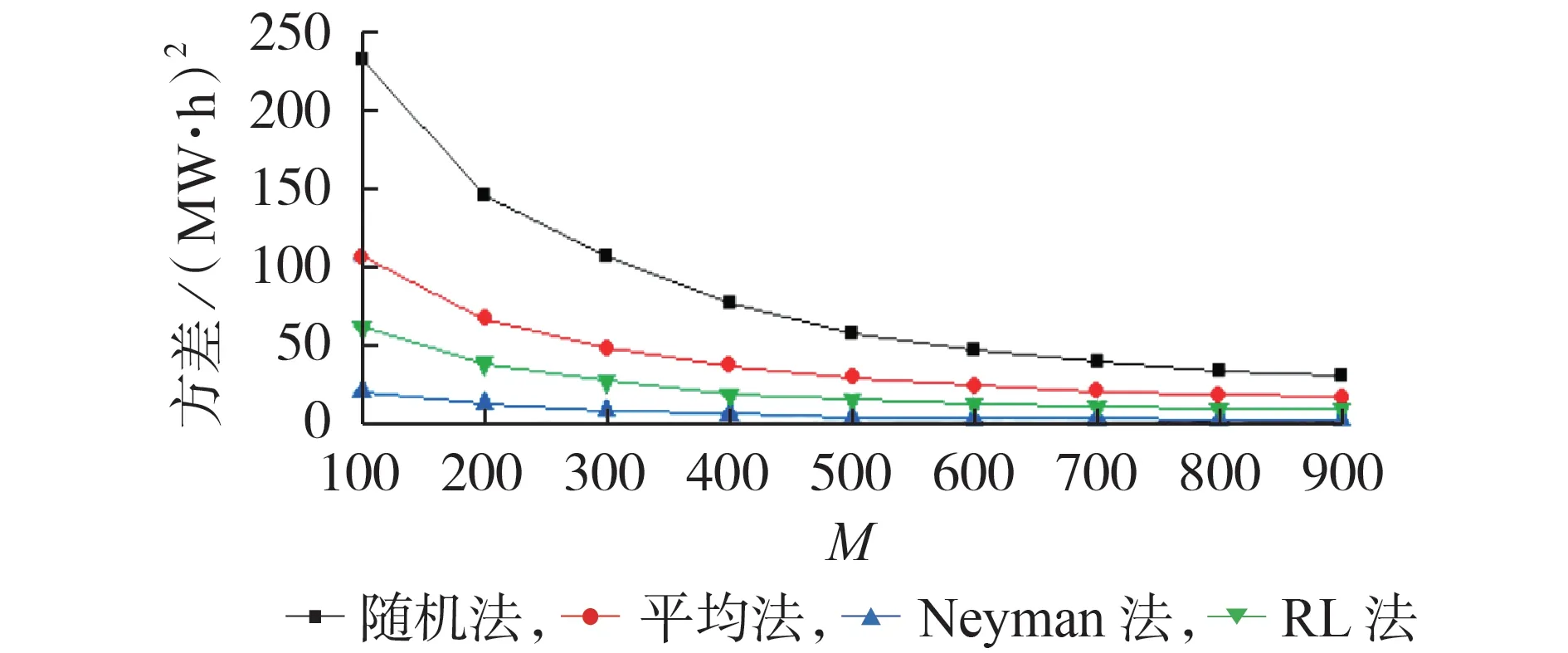
图3 在不同样本量分配方法下SSVE法样本均值的方差Fig.3 Variance of sample mean for SSVE method under different sample distribution methods
由图3 可知,随着样本量M的增大,在不同样本量分配方法下SSVE法样本均值的方差均持续降低,因此SSVE 法具有渐近可靠性。4 种样本量分配方法下最优分配结果的方差大小排序为Neyman 法
4 种样本量分配方法在达到相近可靠性所需要的样本量M和耗时如表2 所示。由表2 可知,RL 法所需耗时最短,是4 种样本量分配方法中计算效率最高的样本量分配方法。
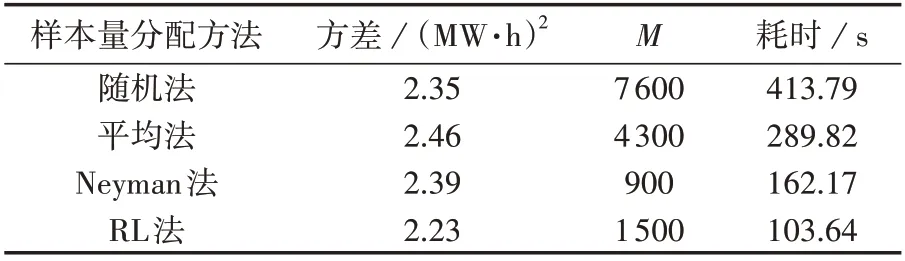
表2 计算复杂度比较Table 2 Comparison of computational complexity
由上述分析可见,SSVE法在解决风-光-水互补发电增益分配问题中具有如下特点。
1)随着样本量的增大,SSVE 法的最优分配结果具有渐近无偏性、渐近一致性和渐近可靠性。当样本量足够大时,SSVE法的分配结果误差率低于0.4%。
2)随机法和平均法直接决定了各层的样本数目,采用该样本量分配方法的SSVE法最优分配结果误差和方差均较大。采用Neyman法的SSVE法最优分配结果误差最小,误差分布最理想且方差最小,但采用Neyman法需要提前计算各层样本的方差,再根据各层方差的比例进行分层抽样,计算量较大。RL法能够利用现有样本信息以迭代的方式探索更多的样本信息,降低了计算量和计算难度,且采用RL 法的SSVE法最优分配结果误差和方差均较小。因此,RL 法能够兼顾估计结果的有效性和估计过程的高效性,适用于解决大规模利益主体环境下风-光-水互补发电增益分配问题。
3)当参与互补优化调度的利益主体数目较少时,与SV 法相比,SSVE 法计算过程复杂、计算量大。但随着利益主体数目增多,SV 法会出现组合爆炸问题,SSVE法的优势逐渐显现。
4.2 37个利益主体风-光-水互补发电
本节算例由雅砻江流域的12 个风电利益主体(编号为1—12)、18 个光电利益主体(编号为13—30)和7 个梯级水电利益主体(编号为31—37)组成,如附录A 图A2 所示。取风电、光电利益主体在2019 年夏季的历史出力数据以及梯级水电利益主体在2019 年6 月14 日的天然来水量数据,建立时段时长为1 h 的日互补优化调度模型,并采用SSVE 法进行互补发电增益分配。
当样本量M分别为6×105和106时,SSVE 法的分配结果如图4 所示。由图4 可知,当M分别为6×105和106时,SSVE 法的分配结果非常接近。SSVE 法与SV 法的计算耗时如表3 所示。由于SV 法需要计算每个互补发电联盟的增益,对于由37 个利益主体构成的风-光-水互补发电系统而言,共需求解约1.375×1012个互补优化调度模型,从而共需计算约1.375×1012个互补发电联盟的增益,因此SV 法计算量大,耗时长。SSVE 法通过分层抽样的方式,只需对各层中的采样联盟进行互补优化调度,计算该采样联盟的增益,因此,SSVE 法极大减少了计算量,缩短了计算耗时,更适用于求解含有大量利益主体的风-光-水互补发电增益分配问题。
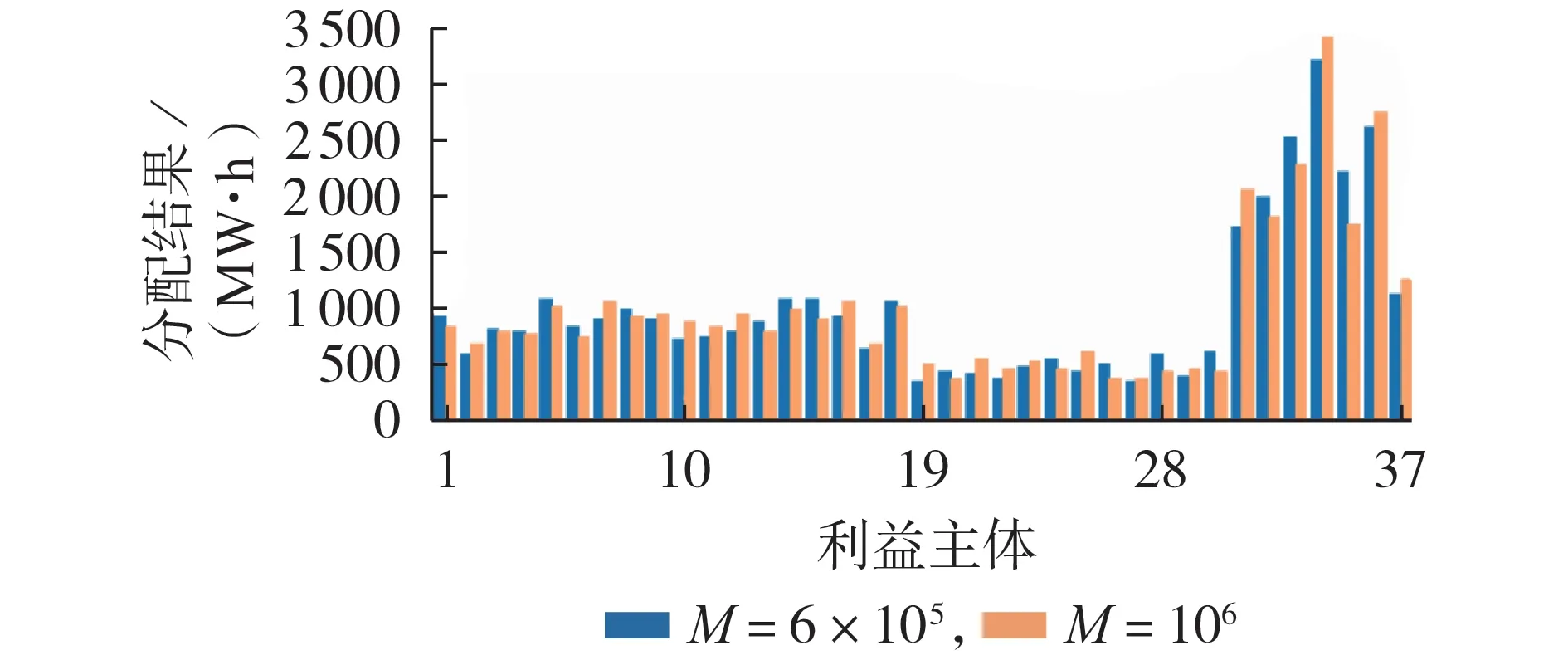
图4 37个利益主体增益分配结果Fig.4 Allocation results of 37 stakeholders
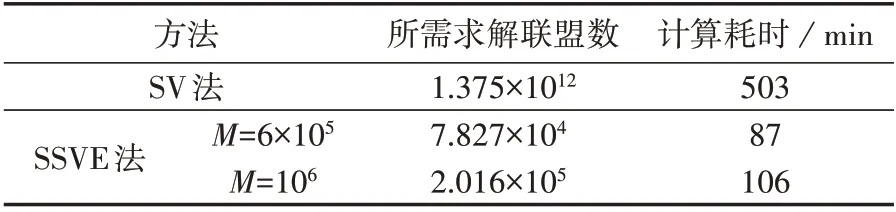
表3 SSVE法和SV法的计算耗时比较Table 3 Comparison of time consuming between SSVE method and SV method
5 结论
对于多利益主体市场环境下的风-光-水互补发电系统,本文建立考虑随机性、波动性以及互补效益的风-光-水互补发电系统联合优化调度模型和独立优化调度模型,提出风-光-水互补发电增益量化方法,进一步提出基于SSVE 法的风-光-水互补发电增益分配方法。通过算例分析不同样本量分配方法下SSVE方法的计算特点,验证了当大量利益主体参与互补优化调度时,SSVE 法能够有效解决经典SV法的组合爆炸问题。
附录见本刊网络版(http://www.epae.cn)。
