电力现货市场环境下园区型综合能源系统多阶段联合优化运行

丁 泉，窦晓波，钱国明，黄 超，陈孝煜，李 鹏

（1. 东南大学 电气工程学院，江苏 南京 210096；2. 国电南京自动化股份有限公司，江苏 南京 210032）

0 引言

2015 年3 月15 日，中共中央国务院发布《关于进一步深化电力体制改革的若干意见》，标志着新一轮电力体制改革启动。作为本轮电力体制改革的重要支撑，国家发改委、国家能源局先后印发系列电力市场配套文件［1-3］，并选择南方（以广东起步）、蒙西、浙江、山西、山东、福建、四川、甘肃等8 个地区作为第一批电力现货市场改革试点。电力现货市场作为连接电力中长期交易与实时运行的关键环节，能充分还原电力商品属性，起到价格发现和资源优化配置的作用，激发市场主体活力，提升电力系统调节能力［4］。我国电力现货市场的参与主体主要包括各类发电／供电企业、售电公司和大用户等［1］，在国内现行市场规则体系下，电力用户有以下2 种方式参与电力现货市场：委托专业售电公司代理进入市场；达到一定用电规模的大用户，可直接参与现货市场。

各类工商业园区大用户一直走在本轮电力体制改革的前沿，以综合能源系统（IES）形式参与电力现货市场，能充分发挥分布式电源、冷热电联供、储能等设备的灵活调控及优化互补能力，更好地适应现货市场灵活多变的电力价格，在面临差价合约及偏差考核的条件下，通过优化运行策略，达到降低用能成本的目的。优化经济运行是IES 的主要研究热点［5-6］。文献［7-9］从日前等较长时间尺度进行了系统性优化，并考虑了一定的随机性影响；文献［10-13］基于多时间尺度优化思想，采用了多种从日前到日内的跨时间尺度联合优化模型。此外，IES在参与电力市场方面的研究也逐渐增多，文献［14］将中长期合同电量分解模型引入电-气IES 日前调度决策过程中，实现了合同电量分解和调度计划的嵌套优化；文献［15］将分布式电源和可调负荷纳入售电公司的优化调度中，建立了以售电公司日前运营收益最大为目标的优化调度模型；文献［16］基于条件风险价值模型，以综合能源服务商在不同类型能源市场中的能源购置成本最小为目标，构建两阶段随机调控模型。综上，目前对IES 参与电力中长期市场已有一定的研究，但大多集中在日前阶段。由于国内电力现货市场试点刚刚开展，电力现货市场环境下的优化经济运行研究不多，特别是在实时阶段较少。考虑到现货市场普遍采用的是差价合约的结算方式，在购电价格实时波动的情况下，对园区型IES 的用能经济优化运行提出了新的挑战。

因此，本文针对我国普遍采用的集中式电力市场运行机制，面向大型工商业园区自主运营的IES，提出了其参与现货市场的优化经济运行模型。对包含热电联供（CHP）机组、电热锅炉、分布式光伏等多类能源供应的IES，首先分析了其参与国内现行电力现货市场的运营模式，以综合用能成本最小为目标，采用多时间尺度多步递进优化的思想，建立了日前、日内、实时三阶段联合优化经济运行模型：在日前市场申报阶段，引入随机优化应对负荷、光伏及日前电价不确定性，考虑中长期市场合同电量的前提下，计算园区IES 最优申报电量；在日内阶段，当确定出清电价后优化计算得到24 h 功率计划曲线；在实时阶段，采用模型预测控制（MPC）算法跟踪现货实时市场电价变化，利用IES 储能、热电互补等综合调节手段，优化校正中长期-日前、日内-实时阶段的偏差电量。算例仿真结果表明，本文所提出的IES 优化经济运行策略可以较好地适应当前国内现货市场机制，最小化园区用能成本。

1 IES在现货市场的运行模式

电力市场改革启动前，园区用户通常采用工商业阶梯电价，在进行经济优化运行时，电价作为常量。而在电力现货市场环境下，电价根据供需关系及网络阻塞不断动态变化，成为时变量。并且，由于差价合约、偏差考核机制，从中长期到日前再到日内实时市场的一系列量、价决策过程都将影响最终用电成本，给IES的经济运行带来挑战。

目前，国内试点的电力市场模式主要分为集中式市场与分散式市场，相较而言，集中式市场模式可以较好地适应电网阻塞，是国内试点的主要模式［5］。本文的研究也将针对该市场模式展开，未做特殊说明情况下，本文所提及的电力市场都为集中式市场。

1.1 IES参与电力市场方式

工商业园区除通过电网获取外部电力供应，往往还包含光伏、CHP 机组、锅炉、储能等多类型能源供应设备，并包含能源服务供应者（ESP）角色，作为工商业园区用户代表，对外负责参与电力市场交易，签订购电合约，直接参与现货市场交易活动，接受电网调度部门电量考核；对内负责运营园区内能源供应设施，安排园区能源在满足供给的前提下以经济性最优为目标。按现有电力市场规则，IES参与电力现货市场的运营方式如图1所示。

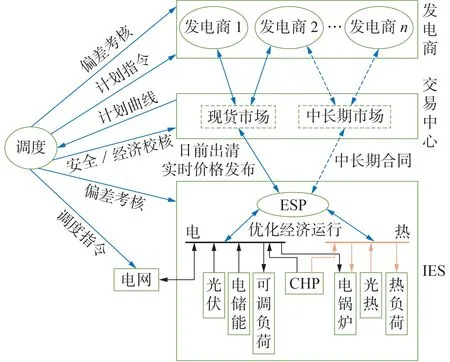
图1 IES参与电力市场的框架Fig.1 Framework of IES participating in electricity market

1.2 现货市场价格模型

国内现货市场一般用差价合约机制，综合中长期市场的偏差考核，允许产生一定偏差收益，形成涉及中长期、日前、实时市场间的量、价差额结算规则，本文参考国内现货市场试点规则［17］，按照差价合约和偏差考核规则，用户电费的计算公式可表示为：

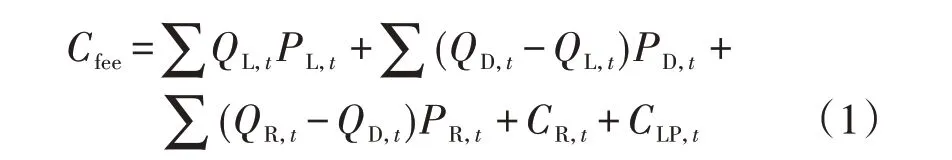
式中：Cfee为用户用电成本；QL，t和PL，t分别为ESP 通过中长期市场签订的金融合约分解到t时段的电量和电价；QD，t为t时段用户在现货日前市场申报用电量；PD，t为t时段现货市场日前交易出清后所形成的日前出清电价；QR，t为t时段用户在现货实时市场中的实际用电量；PR，t为t时段现货市场实时交易中的实时电价；CR，t为t时段现货市场转移收益［17］，表示用户在现货市场内因为市场价格和用电计划偏差而产生的允许收益，计算方式如式（2）和式（3）所示；CLP，t为t时段偏差考核成本，表示将中长期协议电量月度偏差考核折算到当日的惩罚成本，计算方式如式（4）所示。

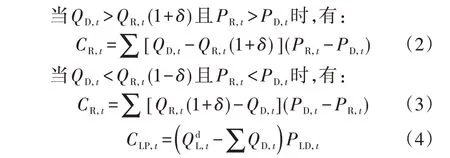
式中：δ为允许偏差范围；为t时段用户中长期协议月度电量在当日的消纳指标，根据不同用户需求，可采用当月剩余完成额与剩余天数之商来进行简化计算，也可根据用户月内用电量分布历史数据进行设定；PLD，t为t时段偏差度电惩罚价格，计算方式由各市场具体规则确定。

IES 对电网售电价格按各地区制定的分布式上网电价进行结算，因单个IES 对市场影响可忽略不计，默认ESP为电力现货市场的价格接受者。

1.3 现货市场下IES联合优化运行模式

电力市场主要包括中长期市场与现货市场，现货市场一般可包括日前、日内和实时3 个市场阶段［4］。本文提出的运行模式在时间尺度上与现货市场同步，围绕日前、日内和实时3 个阶段，实现多步递进的经济滚动优化调度，现货市场下IES 运行模式如图2所示。

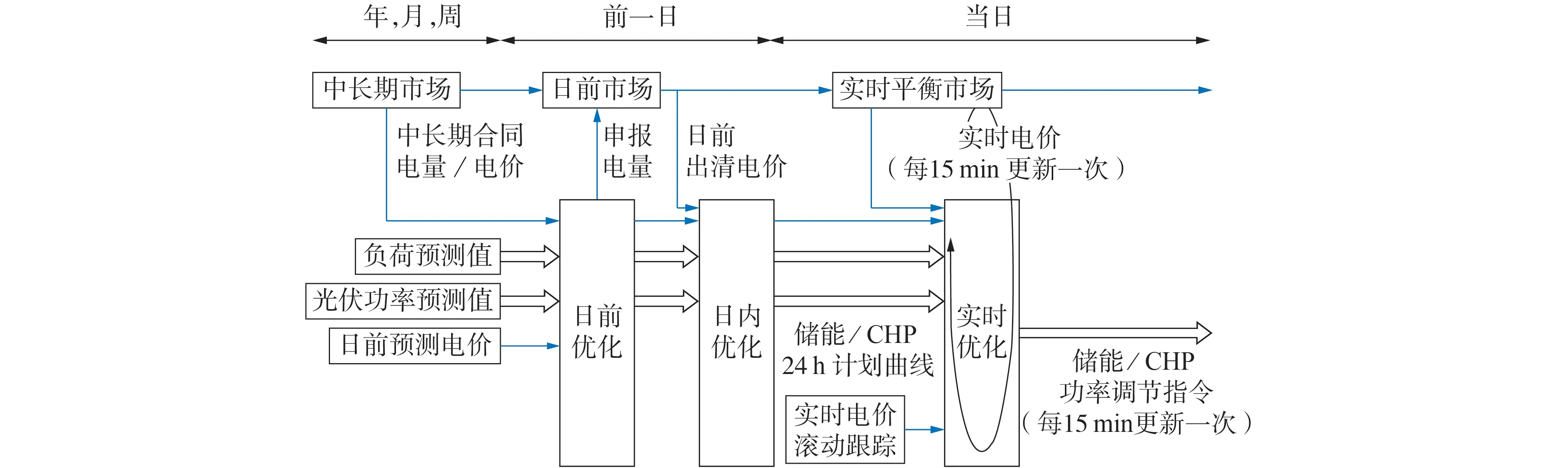
图2 IES在电力现货市场中的运行模式Fig.2 Operation pattern of IES in electricity spot market

1）日前优化。

国内试点省区现货市场下，ESP 需每日申报下一日的分时负荷曲线，参与现货日前市场。如果申报策略与日前出清电价和实时电价趋势不同，将面临因价格偏差导致的额外用电成本，因此，在日前申报阶段的用电负荷申报曲线将直接影响其参与现货市场的收益。

在电量申报阶段需对所申报的负荷曲线进行优化，以园区内下一日综合用能成本最小为目标，基于对负荷、光伏功率的随机概率约束［18］，并考虑分布式电源的功率约束和经济性成本，以及日前电价与中长期合同电价间的偏差电量，通过优化计算得到下一日最优的电网购电曲线，用于日前市场申报。

该阶段假定实时电价等于出清电价，按照中长期合同电量与日前电价及申报电量形成的差价合约，基于式（1）该阶段电费Cfee_da计算公式可简化为：

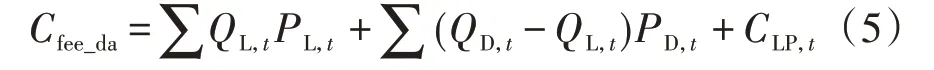
2）日内优化。

进入日内优化阶段，出清电价已经发布，日前市场的现货价格最终确定，在进入实时运行前，需重新修正在电量申报阶段所进行的优化计算，用于提前安排IES 日内发用电计划。日内优化计划与日前优化模型基本相同，区别是根据已出清的日前价格，并基于对实时电价的预测，采用式（1）计算电网购电成本，结合CHP 机组、电锅炉等设备的调节能力，保持日内总体用能成本最小为目标，对系统各可调功率曲线进一步进行优化计算，获得日内24 h 功率计划曲线，包括电网购电计划曲线。

3）实时优化。

进入实时阶段后，配合现货日内实时市场所采取的滚动优化出清方式，在日内实时阶段同步进行滚动优化，以15 min 为周期，更新IES 内部发用电计划曲线和最新的实时市场电价。

实时滚动优化阶段主要完成2 个任务：①与现货实时市场同步，按照固定周期对发布实时电价进行跟踪预测，在差价合约允许偏差范围内，优化CHP机组、电锅炉及储能系统功率，降低IES 从大电网购电的成本；②以日前发用电计划曲线为参考，根据对负荷、分布式发电功率的超短期预测，以综合用能成本最低为目标，校正日前计划偏差，实现日内全局计划与实时阶段局部优化间的协同。

2 系统模型

2.1 园区IES模型

工商业园区IES典型结构分为能源供给、能源转换、能源存储、能源消费4个主要部分，如图3所示。

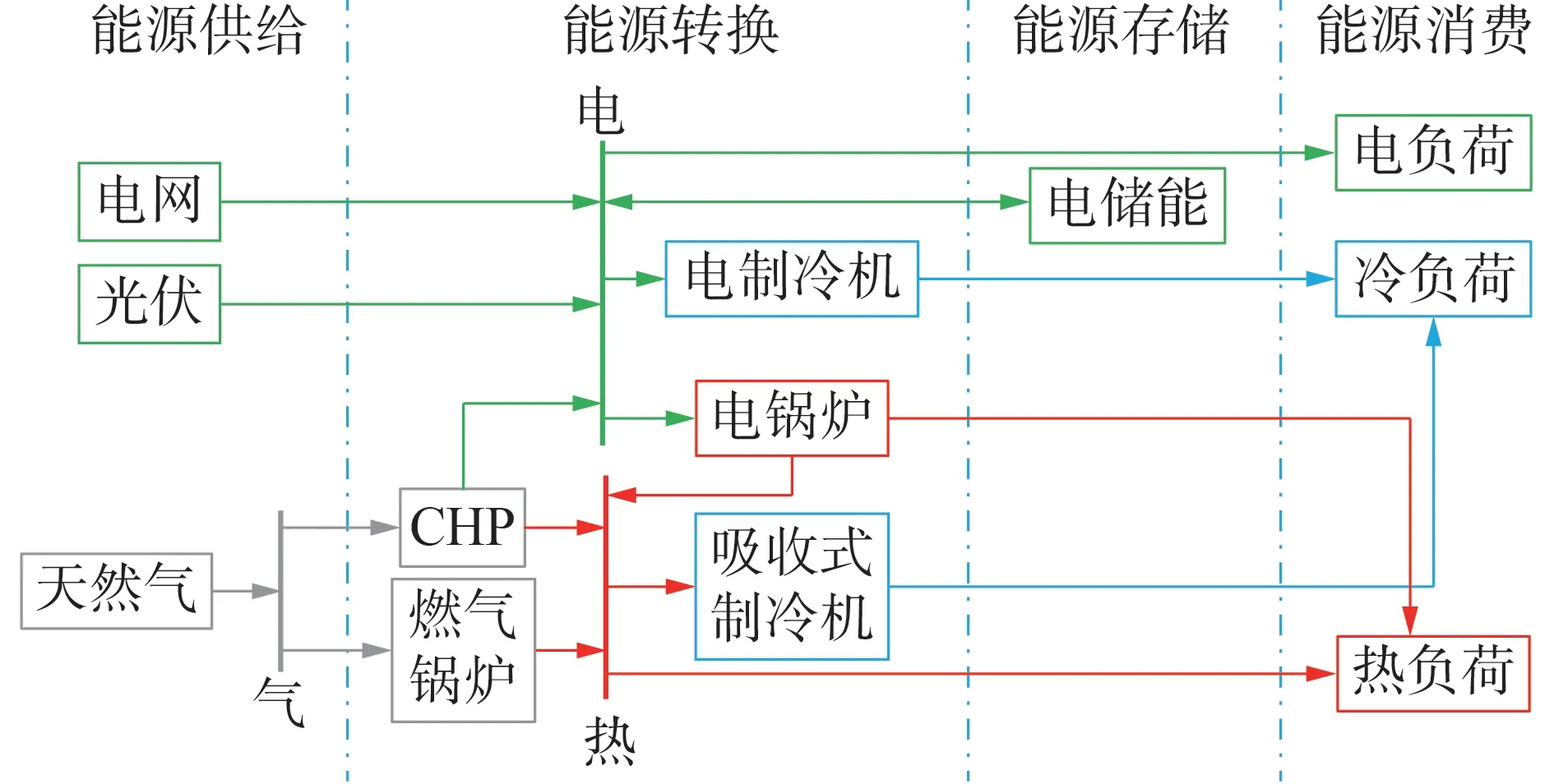
图3 典型工商业园区IES框架Fig.3 Typical framework of industry and commercial park-level IES

2.2 设备模型

1）光伏发电设备。

光伏发电功率计算方法如下：

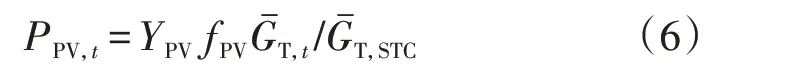
式中：PPV，t为t时段光伏发电功率；fPV为光伏阵列降额因数；YPV为光伏阵列容量；-GT，t为t时段到达光伏阵列的辐照度；-GT，STC为辐照度标量，取1 kW／m2。模型中假设光伏阵列都采用最大功率点跟踪控制。

2）电锅炉。

电锅炉模型表示如下：

式中：PEB，t为t时段电锅炉耗电量；HEB，t为t时段电锅炉产热量；ηEB为电热转化效率。

3）制冷机设备。

制冷机设备可分为电制冷机和吸收式制冷机，模型分别表示如下：

式中：PAC，t为t时段电制冷机耗电量；HLBR，t为t时段吸收式制冷机耗热量；CAC，t、CLBR，t分别为t时段电制冷机、吸收式制冷机产冷量；ηAC、ηLBR分别为电冷转换系数、热力系数。

4）CHP机组。

式中：GCHP，t为t时段CHP机组燃气总功率；HCHP，t、PCHP，t分别为t时段CHP 机组产热量、发电量；ηH，CHP、ηP，CHP分别为CHP机组的气热转化效率、气电转化效率。

5）储能设备。

储能设备在充放电过程的状态方程如下：

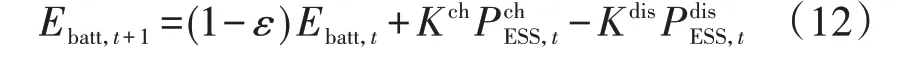
式中：Ebatt，t+1和Ebatt，t分别为t+1、t时段储能设备存储容量；Kch、Kdis分别为储能设备充、放电效率；、分别为储能设备的充、放电功率；ε为自损耗系数。

2.3 约束条件

1）功率平衡约束。

IES内需保持电、热系统的功率平衡：

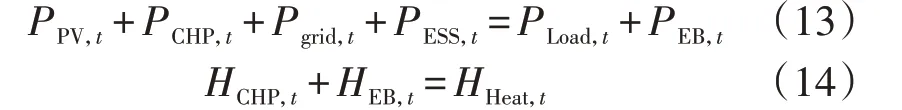
式中：Pgrid，t、PESS，t、PLoad，t分别为t时段电网、储能功率和电负荷；HHeat，t为t时段热负荷。

2）设备约束。

其他设备的约束条件详见附录A。

3）概率约束。

考虑系统内电热负荷及光伏发电功率的不确定性对电网购电决策的影响，采用随机优化中的概率约束模型对购电量进行一定裕度的设置。

式（13）、（14）包含了电热负荷及光伏预测值等不确定因素，因此以概率约束的形式对其进行转化：

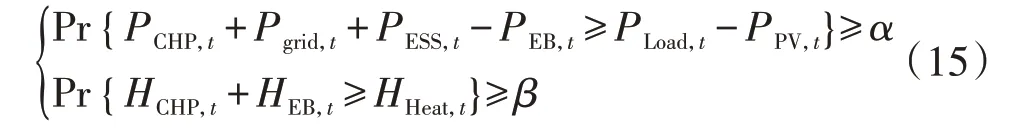
式中：Pr{·}表示条件{·}成立的概率；α、β分别为电、热概率约束成立的置信度。

假设光伏出力预测、负荷预测误差服从正态分布，则式（15）可转化为：

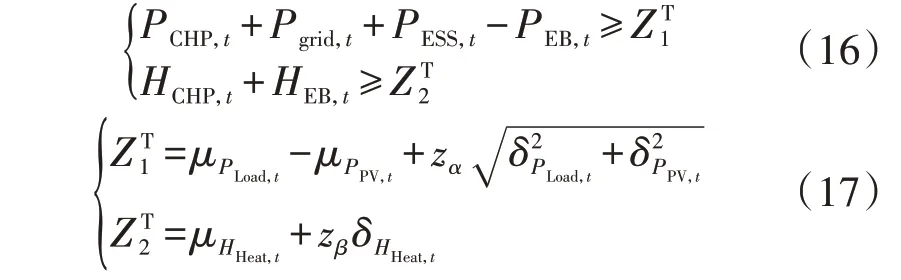
式中：μ、δ分别为对应的期望值、标准差；zα、zβ分别为服从标准正态分布的α、β分位数。

3 IES在现货市场的优化模型

基于1.3 节所提出的IES 在现货市场的运行模式，本节给出日前、日内到实时阶段的跨时间尺度优化模型。

3.1 日前、日内优化

日前、日内优化模型基本一致，主要区别在于日前优化基于对日前电价的预测价格进行优化计算，日内优化则是基于确定的出清价格。并得到日内24 h功率计划曲线。

日前市场电量申报模型的目标函数为经济性最优，即总运行成本最低：

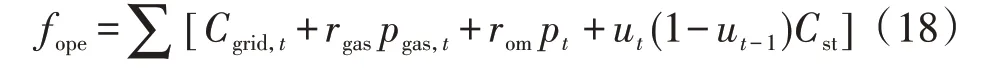
式中：pgas，t为t时段天然气的能源消耗功率；rgas为天然气的单位耗量成本；pt为t时段储能设备输出功率；rom为单位功率运行维护成本；ut为0-1变量，表示t时段CHP 机组启停状态，取值为1 时表示启动，取值为0 时表示停机；Cst为启动成本；Cgrid，t为t时段日前电费成本，可采用式（5）计算得到。

3.2 基于MPC的实时滚动优化

在现货市场环境下，除了光伏发电、负荷功率具有一定的随机性外，实时市场中的电价也将呈现一定的不确定性。MPC适合解决含不确定因素的系统优化控制问题，其实质是一种基于滚动时域的优化控制方法，不仅能处理外部干扰，对不确定性因素也具有很强的处理能力［19］。

1）现货实时市场下MPC滚动优化策略。

MPC 以一定的计划曲线作为跟踪目标，通过建立预测和控制2 个滚动时域，在实时运行阶段根据最新的预测数据和实际运行数据进行不断的优化与反馈校正，电力现货市场下MPC 原理如附录B 图B1所示。

考虑到日内计划采用24 h 短期预测，已有较高的预测精度，以3.1节中生成的日内24 h功率计划作为MPC 的参考曲线，由超短期光伏、负荷与实时电价短期跟踪预测，动态调整实时下发功率计划指令。

现货实时市场下的MPC 滚动优化策略主要包括以下3 个步骤：①在当前k时刻获取当前状态x(k)，基于对光伏、负荷和日内现货市场实时电价的预测模型，在预测域时间窗k+Np范围内，跟踪日前功率计划曲线，通过滚动优化算法，计算得到该时间段内的预测功率曲线，并计算得到控制域时间窗k、k+1、…、k+Nc时刻的控制指令序列u(k+i|i∈[1，Nc]) ，并以Δt为时间间隔；②将控制指令序列的第一个值u(k)应用于控制对象，并产生系统输出向量y(k)；③到k+1时刻，更新状态，并将y(k)反馈到滚动优化输入量，用于校正上一时刻扰动量r(k)以及预测误差，并循环重复以上步骤。

2）基于MPC 的滚动优化模型。选取储能充放电功率Pbatt(k)、储能系统荷电状态SSOC(k)、电锅炉制热功率PEB(k)、CHP 机组燃气总功率GCHP(k)、微电网与外电网联络线交换功率Pgrid(k)构成的向量为状态向量x(k)：

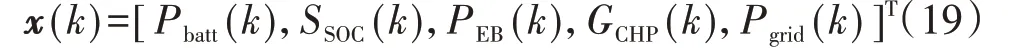
选取储能、电锅炉和CHP 机组的出力增量ΔPbatt(k)、ΔPEB(k)和ΔPCHP(k)构成的向量作为控制向量u(k)：

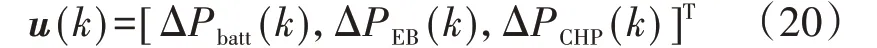
选取光伏日内预测功率增量ΔPPV(k)，电、热负荷的日内预测功率增量ΔPload_elc(k)、ΔPload_heat(k)构成的向量作为扰动向量r(k)：

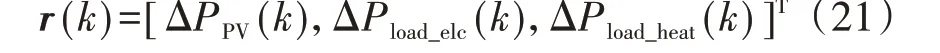
利用MPC建立状态空间模型，如式（22）所示。

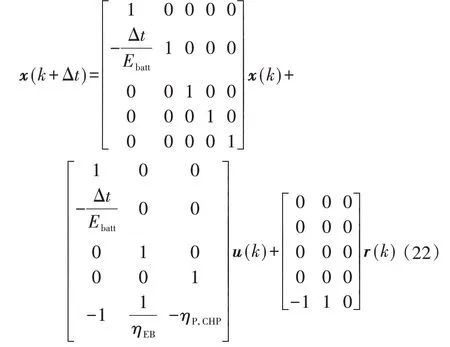
选取储能荷电状态、电网联络线功率构成的向量作为用于日内跟踪的输出向量y1(k)：

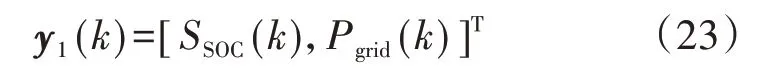
选取CHP 输出电功率、微电网与外电网的联络线功率构成的向量作为用于计算日内购电、购气成本值的输出向量y2(k)：

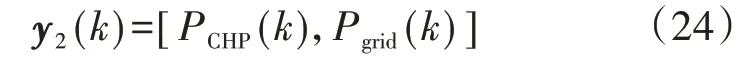
通过对状态空间预测模型反复迭代，便可得到输出向量在预测时长Np内的跟踪输出向量Y1以及成本值输出向量Y2，分别如下：

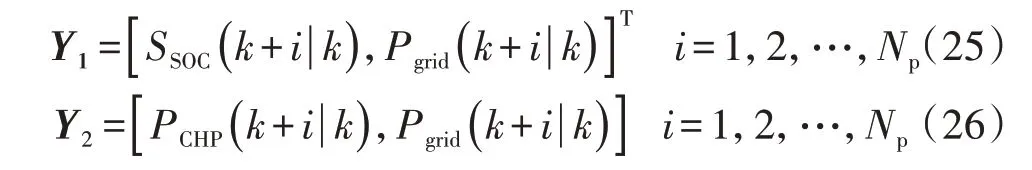
本文选取联络线功率计划值和储能荷电状态的日内优化值作为跟踪目标，建立了预测时域和控制时域递减的滚动优化模型，目标函数如下：

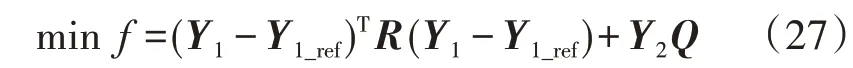
式中：Y1_ref为输出向量Y1的日前计划值构成的向量；R为跟踪误差的权重系数矩阵，如式（28）所示；Q为各时段购电、购气价格矩阵，如式（29）所示。

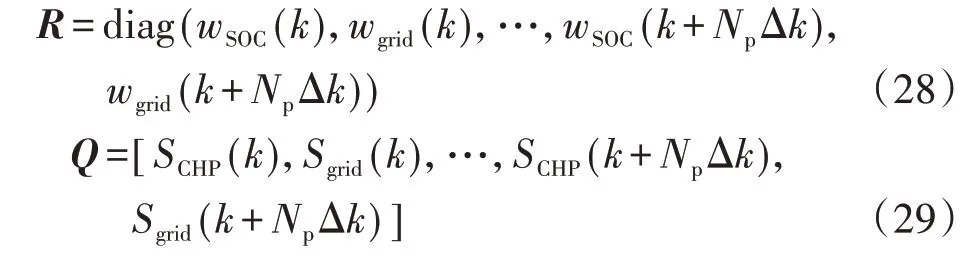
式中：wSOC、wgrid分别为储能和电网购电的跟踪权重系数，由于日内滚动优化以IES 总运行成本最低为目标，较注重短时局部经济性，为保证24 h内的全局优化，通过跟踪误差的权重系数矩阵R中的跟踪权重系数来协调系统全局和局部的经济最优性，具体的取值方式见文献［10］；SCHP、Sgrid分别为天然气和电网购电价格。

4 仿真算例

选取南京市某企业园区IES 进行算例验证，该系统含电、气2 种能源输入形式，其结构见图4，园区中各设备的相关参数以及天然气热值、价格见附录B 表B1。电力市场数据来自于国内某电力现货试点省份2020 年8 月26 日的实际电价数据，算例仿真的计算环境为Intel Core-i5 2.3 GHz，8 GB RAM。

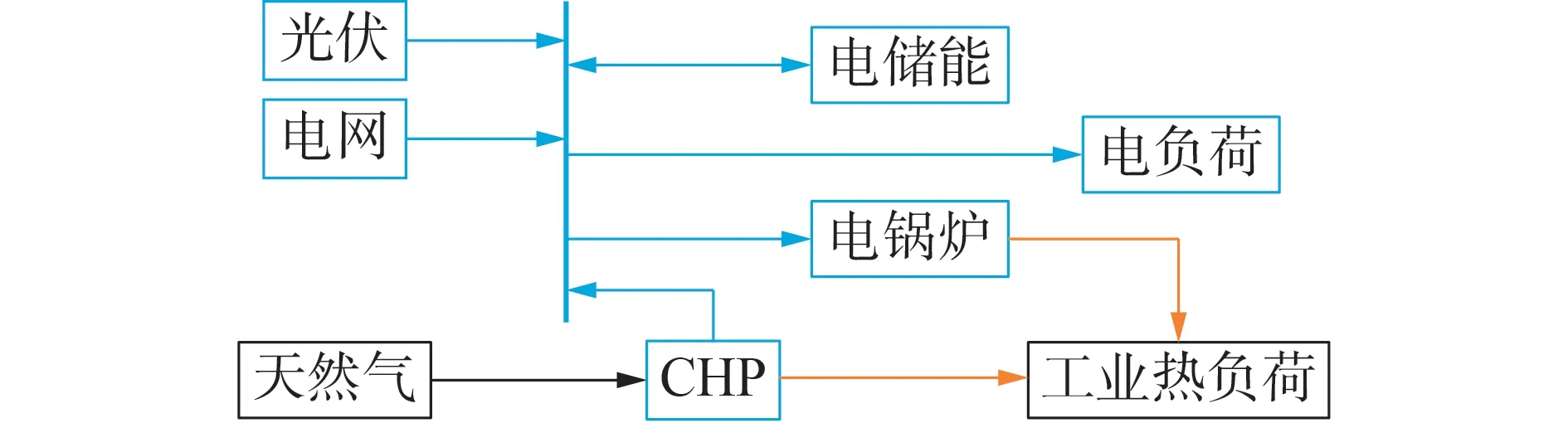
图4 IES仿真系统结构Fig.4 Structure of IES simulation system

4.1 日前、日内阶段优化

按照1.3节中的阶段性联合优化方案，采用CPLEX求解器求解日前（日内）阶段优化仿真模型。由于在该阶段无法获得实时电价，因此购电成本主要考虑式（1）—（3）中长期与日前电价的差价合约。该日的长期合同电价、日前预测电价和日前出清电价曲线如图5所示。

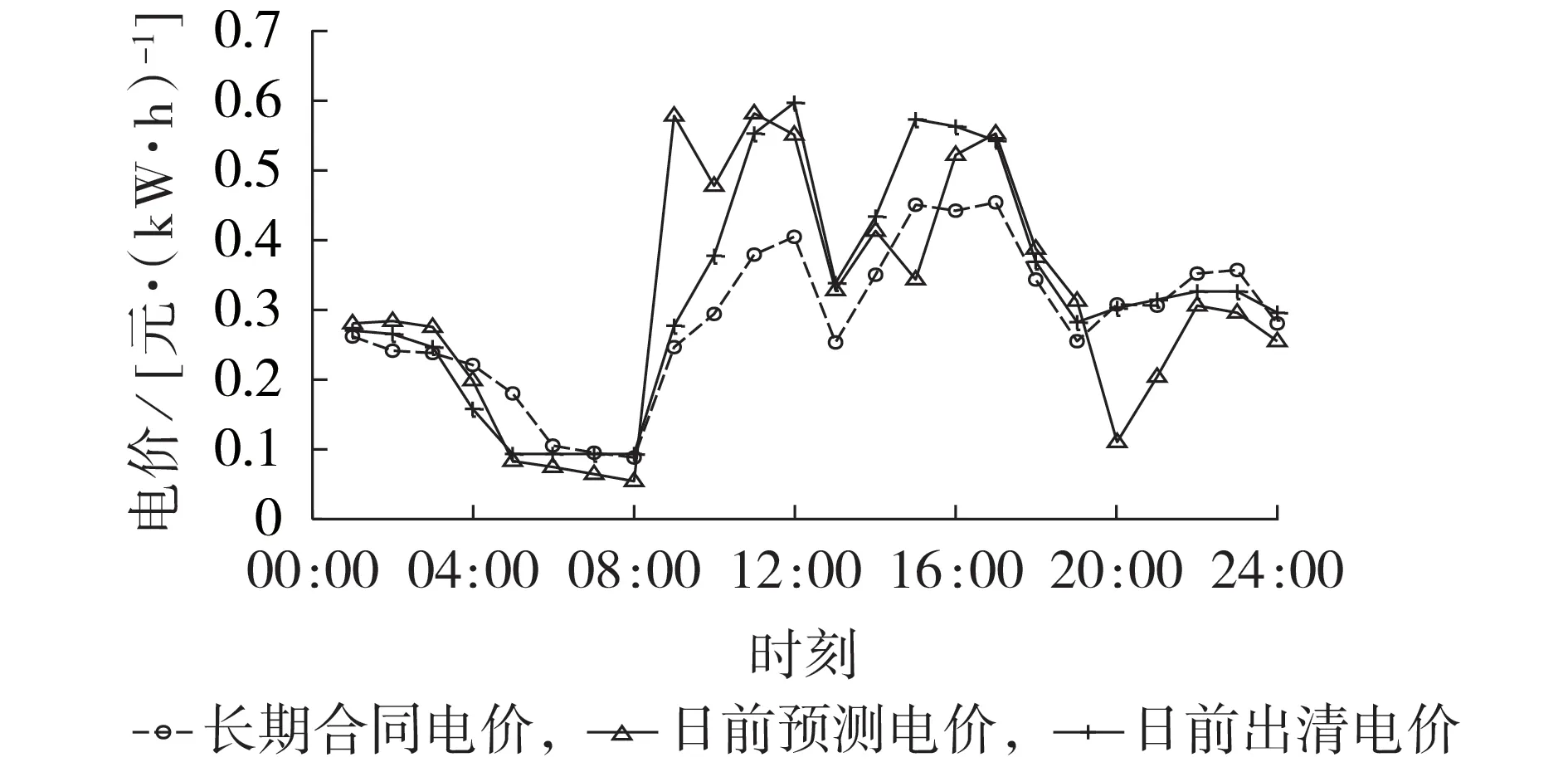
图5 电价曲线Fig.5 Curves of electricity price

1）随机优化。

假设光照强度、负荷预测均服从以预测值为期望、一定标准差的正态分布，不同置信度下的运行成本如图6 所示。由图可知，置信度越高，系统运行成本越高。综合以上分析，本文中可靠性指标取值为0.95，此时冷热电系统供能相比需求量而言都留有一定裕度，以确保不确定条件下的运行经济性。

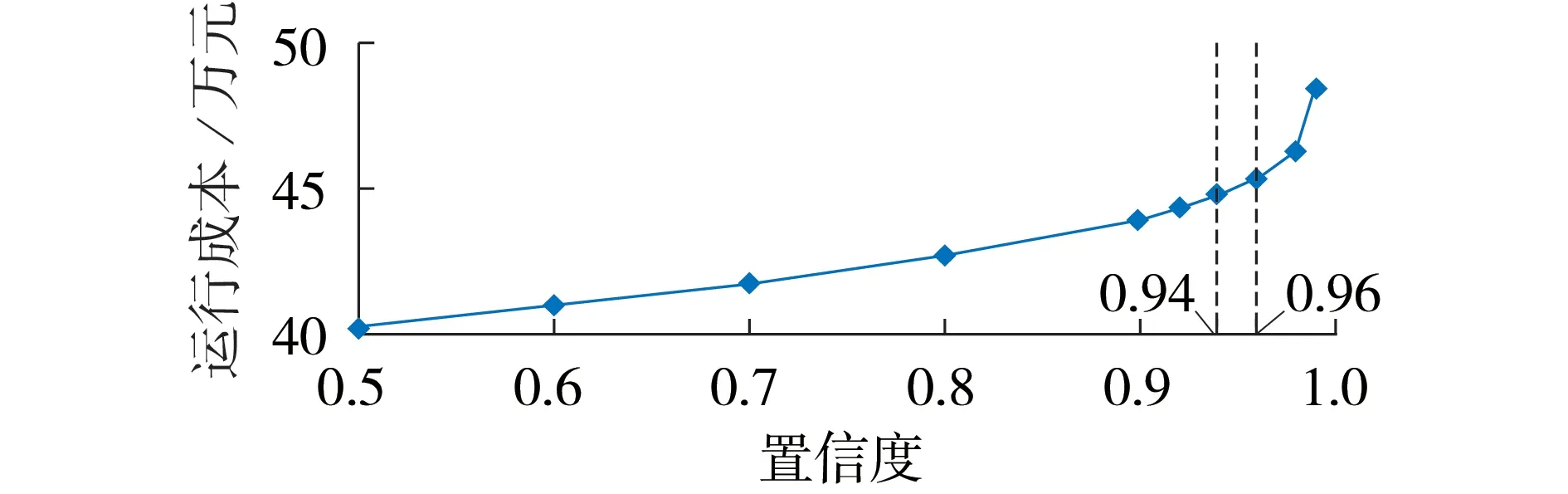
图6 不同置信度下的运行成本Fig.6 Operating cost under different confidence degrees

2）日前优化。

根据式（5）计算日前阶段的购电成本，优化得到的主要设备功率计划曲线及最优的电网购电负荷申报曲线如图7 所示。由图可知，由于CHP 机组供能转化效率高，综合成本较低，在用热负荷升高并且预测到日前电价较高阶段（09:00开始），优先采用CHP机组发电并供热，从而降低电网购电成本。

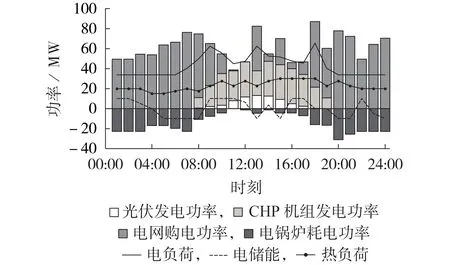
图7 日前阶段优化计算结果Fig.7 Optimized calculation results in day-ahead stage

3）日内优化。

进入日内优化阶段，出清电价已经发布，在此基础上再引入对实时电价的预测，形成结合CHP 机组、电锅炉等能源供应的优化调节效果，对系统各可调功率曲线进一步调节，获得第二天24 h 优化经济曲线及功率计划曲线，如图8所示。

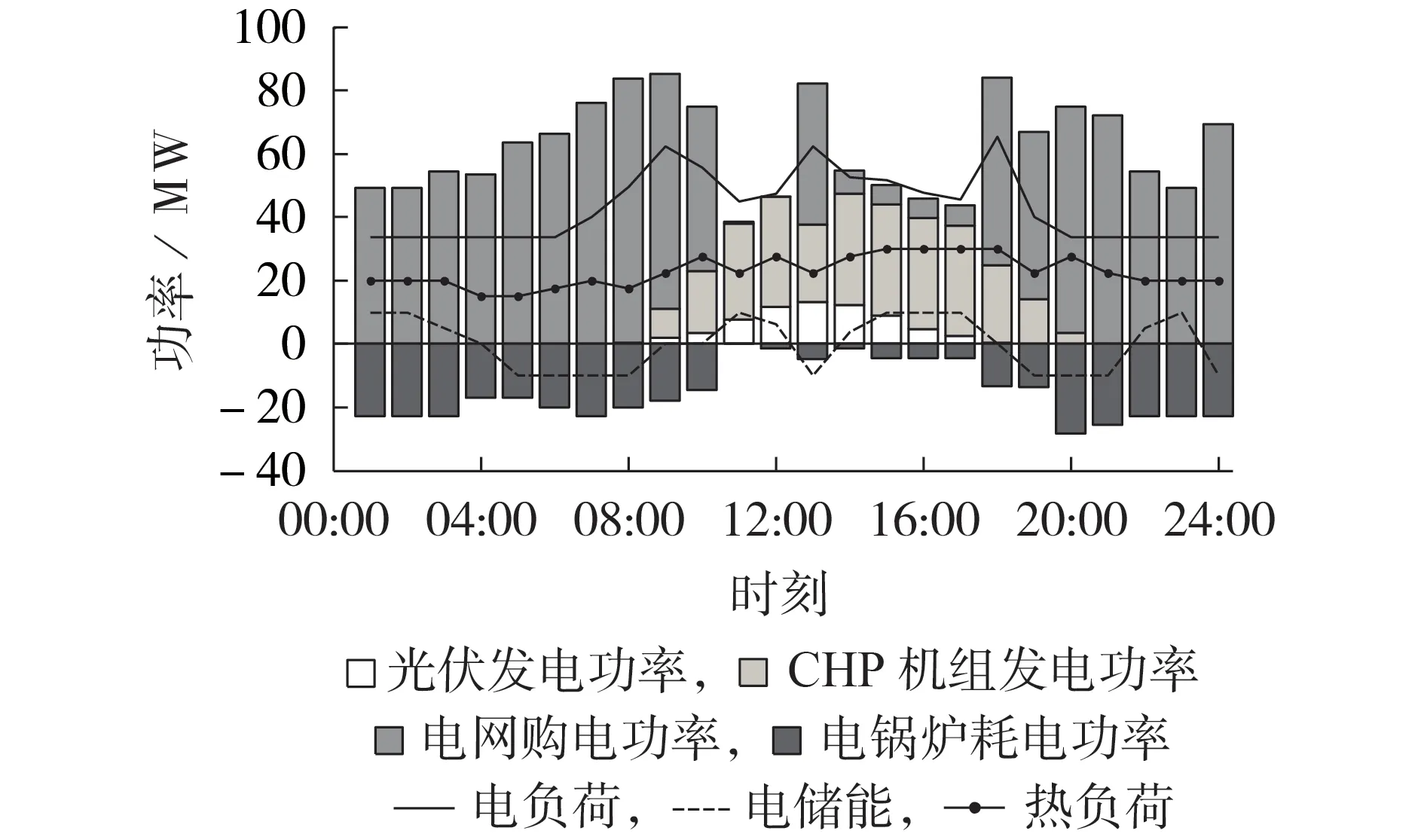
图8 日内阶段优化计算结果Fig.8 Optimized calculation results in intraday stage

由图8 可知，CHP 机组的日内优化运行曲线基本与日前一致，但是在09:00—10:00时段，出清电价明显高于日前预测电价，此时采用CHP 机组消耗天然气为电负荷供电更便宜，因此为了增大该时段CHP机组的发电量，考虑到爬坡约束，将其提前了1 h，于07:00 开机。在15:00 和20:00—11:00 时段，出清电价明显低于日前预测电价，此时采用电网购电更便宜，因此逐渐减少CHP机组的发电量。

日前与日内阶段电价及CHP 机组出力对比如附录B图B2所示。

4.2 实时优化

本文重点验证实时滚动优化效果，因此有关光伏、负荷、电价等预测算法，不再赘述。为不失一般性，假定实时阶段的光伏发电、负荷、电价等日内预测数据，在实际数据基准上叠加符合正态分布的误差进行模拟。实时电价采用现货市场每小时出清电价数据，并在其基础上每15 min 叠加小于20%的随机波动。

MPC 的模型参数如下：预测域时长为2 h，控制域时长为1 h，实时滚动优化调度每15 min 执行一次，跟踪权重系数为10-6。

1）实时滚动优化效果。

以日内预测值为期望，标准差取5%，模拟光伏、负荷及实时电价曲线。图9 为实时滚动优化期间，CHP机组发电功率和电网交换功率的实际计划曲线。

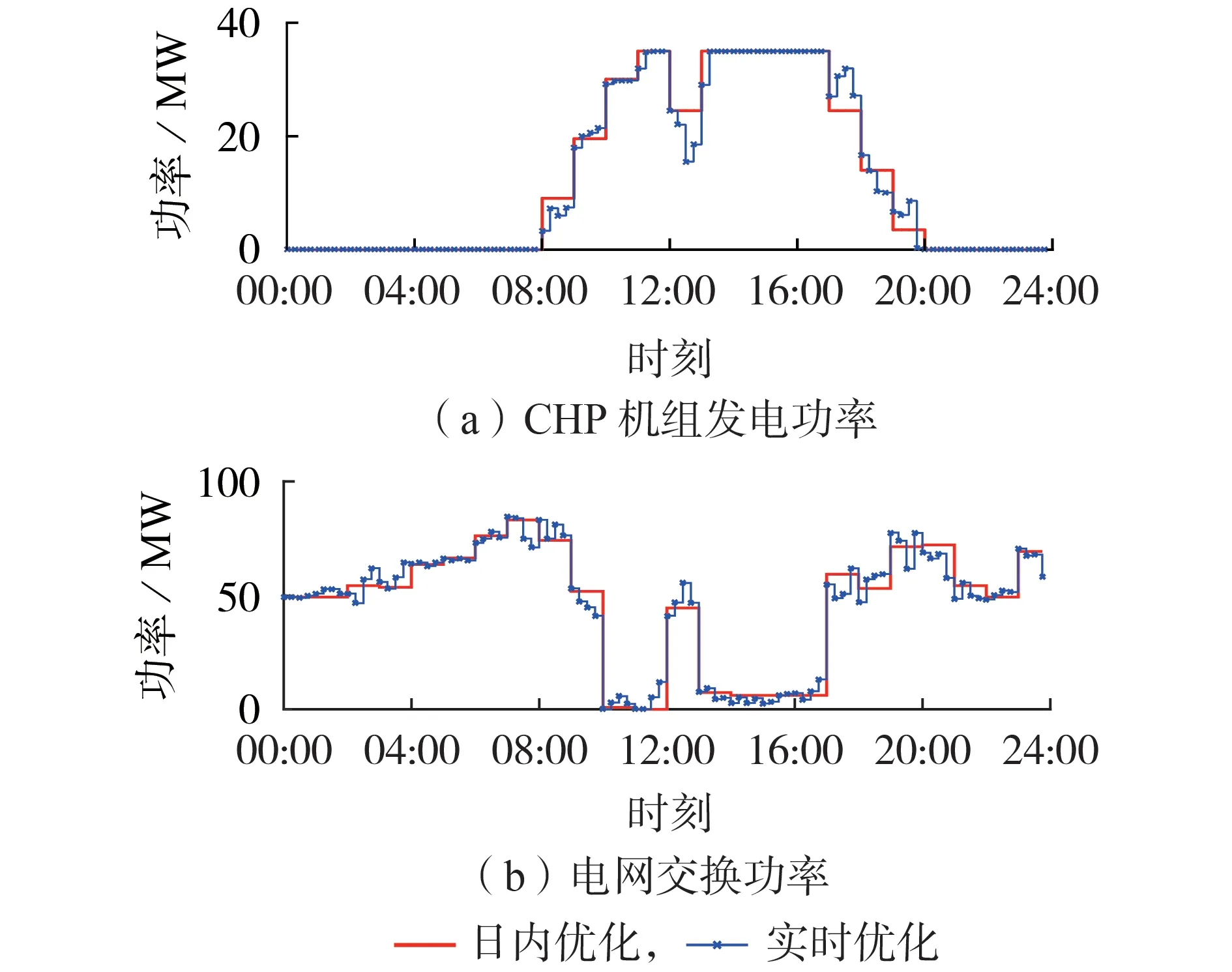
图9 实时阶段滚动优化结果Fig.9 Results of rolling optimization in real-time stage

从图9 中可以看出，当日内预测数据与实时阶段实际数据间误差正常的情况下（标准差取5%），实时滚动优化算法将以跟踪日内优化计划曲线为主，此时更多反映全局的优化效果。实时滚动完整优化计划曲线如附录B图B3所示。

2）电价扰动下滚动优化效果对比。

为观测本文实时滚动优化模型的抗扰动能力，在出清电价的基础上，对15:00—17:00 时段实时电价模拟60%的扰动，此时的CHP 机组发电功率、电网交换功率和电锅炉耗电功率的实际计划曲线如图10所示。

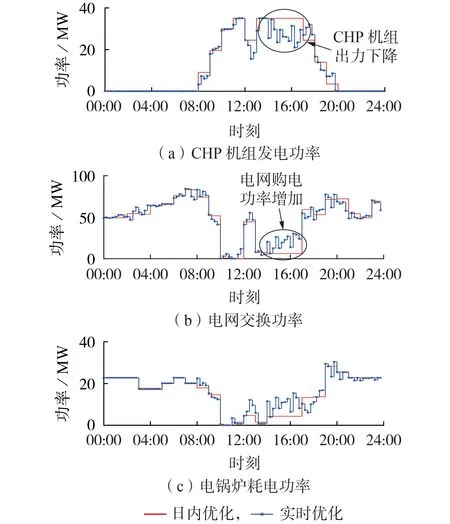
图10 电价扰动情况下的滚动优化结果Fig.10 Results of rolling optimization under disturbance of electricity price

由图10 可以看出，在15:00—17:00 时段，由于实时电价相较于日前出清电价有了明显下降，实时滚动优化对日内24 h 功率计划进行了一定程度调整，电网购电量有所增加，CHP 机组出力显著下降，电锅炉耗电明显上升。滚动优化对实时电价的波动进行了适时的调整，15:00—17:00 时段内的用能成本下降了4.31%，电价扰动下的系统实时滚动优化对比如表1所示。

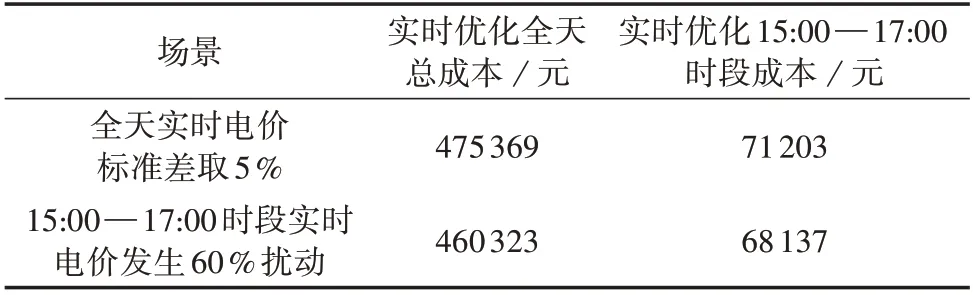
表1 电价扰动下的经济性对比Table 1 Economic comparison under disturbance of electricity price

实时电价扰动情况下的完整滚动优化计划曲线如附录B图B4所示。

5 结论

本文针对园区型IES，建立了其在我国最新电力现货市场试点规则下的联合优化经济运行模型，该模型具有以下特点：①电价信息不再作为参数量，而是以时变量形式在日前、日内和实时滚动阶段分步骤予以预测与修正，与电力现货市场差价合约机制进行同步对接；②在现货市场阶段充分考虑了中长期市场及光伏、负荷随机性波动的影响，解决了日前市场最优电量申报问题；③引入MPC 算法实现运行阶段滚动优化，综合考虑了日前全局性优化和局部优化的协同，并解决在此期间出现的不确定性问题。

算例仿真结果表明，本文所提出的电力现货市场环境下的园区型IES 联合优化经济运行模型，可以较好地适应我国现行电力市场运行规则，实现了分阶段逐级优化目标，是IES 参与电力现货市场的一种有效经济性运行方法。目前，本文研究还主要基于仿真数据，未来还需进一步结合实际运行数据，验证其算法的适应性与鲁棒性。

附录见本刊网络版（http：//www.epae.cn）。