含分布式光伏的主动配电网电压分布式优化控制

2021-09-14张东辉张儒峰李国庆

电力自动化设备 2021年9期

姜涛，张东辉，李雪，张儒峰，李国庆

（东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林吉林 132012）

0 引言

近年来，随着配电网中分布式电源接入比例不断提高，特别是分布式光伏PV（PhotoVoltaic）的大量并网，配电网潮流逆向流动更加频繁，导致配电网电压分布发生剧烈变化；同时，PV 出力的不确定性导致配电网电压波动和越限等问题愈发突出［1］，给配电网的安全运行带来了巨大挑战。

传统的配电网运行常利用电容器组和有载调压器等设备解决PV大规模并网带来的电压越限问题，但其调节速度慢且会增加投资成本，若频繁调节还将导致设备使用寿命下降。分布式PV 在并网发电过程中，除了可输出有功功率外还具有一定的无功功率调节能力［2］，通过在一定范围内调节PV 的无功功率输出，可改善配电网电压质量，降低网络损耗。同时，当PV出力大、负荷小时，可适当削减有功输出，增强无功调节能力，改善配电网运行状况［3］。因此，在主动配电网中，合理地优化控制分布式PV的有功和无功输出，对保障配电网安全、经济运行意义重大。

目前，含分布式PV的主动配电网电压优化控制方法主要分为以下3 种：本地优化控制、集中式优化控制和分布式优化控制。文献［4］提出了一种基于PV 无功调节的主动配电网本地电压控制策略；文献［5］提出了基于分布式电源有功、无功调节的本地电压控制策略，以改善配电网电压质量。它们都具有响应速度快、不需要通信网络等优点，但缺乏对分布式PV全系统范围的协调，无法实现电压的全局最优控制。文献［6］提出了一种PV逆变器集中／本地两阶段电压／无功控制方法，弥补了采用本地控制难以实现整体协调的不足，但存在单点故障、通信计算负担大及信息私密性差的弊端。文献［7］提出了一种基于电压灵敏度的电压协调控制方案，利用叠加定理求得电压越限节点对不同位置PV 的灵敏度因子，然而该控制方案通信负担重，并且计算量大。文献［8］提出了一种配电网分布式电压控制策略，采用分布式紧急控制时先利用下游节点再利用上游节点PV 提供电压支持。文献［9］针对PV 渗透率过高导致电压越限的问题，提出了一种两级电压／无功分布式控制策略调节PV 逆变器的无功输出。文献［8-9］提高了电压调节能力，但未采用对配电网进行分区的分布式优化控制，优化效果有限。配电网的电压分区分布式优化控制方法，通过配电网分区和多区域间协调，不仅能实现电压的全局最优控制，还可以降低计算复杂度，提高优化计算效率，具有良好的优化效果。然而，目前含分布式PV的主动配电网电压分区分布式优化控制仍处于初步研究阶段。

近年来，交替方向乘子法ADMM（Alternating Di⁃rection Method of Multipliers）已成为求解电力系统分布式优化控制问题的重要方法。文献［9-10］均以节点为单元构建了基于ADMM的分布式PV无功分布式优化控制方法。文献［11］提出了一种基于ADMM的主动配电网日前两阶段分布式优化调度策略。然而，在求解过程中，上述文献采用的ADMM 易出现迭代次数过多、计算速度慢等问题［12］。因此，研究ADMM 的加速方法以提高主动配电网电压分布式优化控制算法的计算效率具有重要意义。

为此，本文提出一种含分布式PV的主动配电网电压分布式优化控制策略。首先，以节点电压偏差、PV 削减量和网损最小为目标构建含分布式PV 的主动配电网电压优化控制模型；其次，利用二阶锥SOC（Second-Order Cone）松弛技术对该模型进行凸化处理；然后，基于分解协调原则将配电网合理分区，构建基于ADMM 的多区域分布式电压协同优化控制框架；进一步地，基于残差平衡原理和松弛技术，提出一种加速ADMM 来改善算法收敛性能；最后，通过IEEE 33 节点测试系统对所提方法进行分析和验证。

1 含分布式PV 的主动配电网电压优化控制模型

本节首先构建含分布式PV 的主动配电网电压优化控制模型，进而利用SOC 松弛技术对该非凸模型进行凸化处理。

1.1 电压优化控制模型

本文的配电网电压优化控制目标为节点电压偏差、PV 削减量和网损最小，其约束条件包括配电网支路潮流约束、运行安全约束和PV 逆变器控制约束。

1.1.1 目标函数

根据配电网不同运行需求，本文拟通过调节分布式PV 的有功和无功输出来实现节点电压偏差、PV 削减量和网损最小的控制目标，因此所建立的电压优化控制目标函数为：

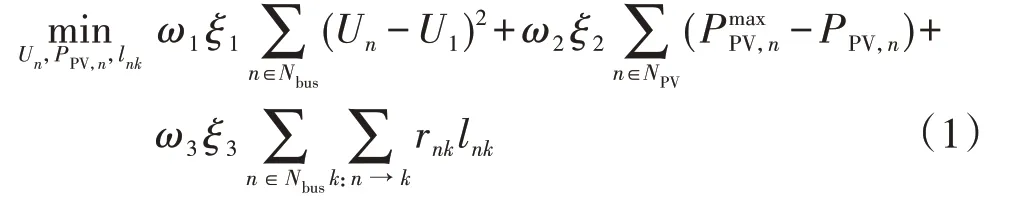
式中：Nbus为配电网中节点集合；Un为节点n电压幅值；设节点1 电压幅值为电压基准值，即U1=1 p.u.；NPV为配电网中接有PV 的节点集合；和PPV，n分别为PV 最大有功输出功率和节点n的PV 有功输出功率；k：n→k表示以节点n为首端节点的支路末端节点集合；rnk和lnk分别为支路n-k的电阻和电流幅值平方；ω1—ω3为最小化权重系数，均大于等于0 且ω1+ω2+ω3=1；ξ1—ξ3为大于0 的校正系数，以保证式（1）中3 项数值为同一数量级。式（1）中第一项为节点电压偏差，第二项为PV削减量，第三项为网损，显然第一项是非线性的。

1.1.2 约束条件

1）配电网潮流约束。

本文的配电网潮流模型采用图1 所示的已广泛应用的配电网支路潮流模型［13］。

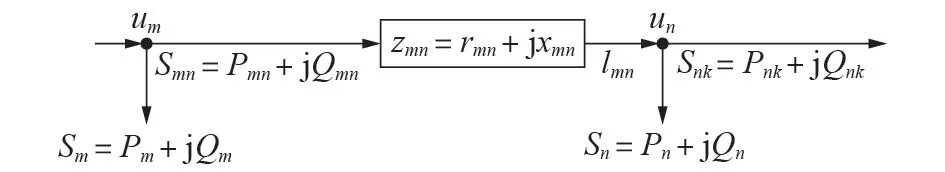
图1 配电网支路潮流模型Fig.1 Branch power flow model of distribution network

图1 中，um、un分别为节点m、n电压幅值的平方；xmn为支路m-n的电抗；Pmn和Qmn分别为由节点m流过支路m-n的有功和无功功率；Pn和Qn分别为注入节点n的净有功负荷和无功负荷。与该支路有关的电流及有功、无功功率约束可表示为：

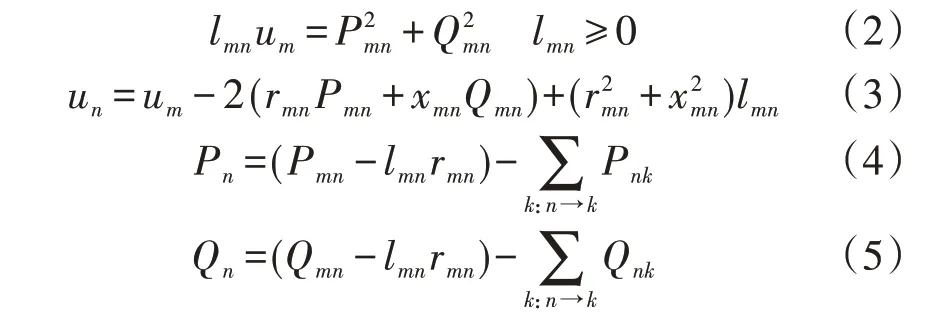
不难看出，式（2）为非凸非线性约束，其他均为线性等式约束。

2）配电网运行安全约束。

为确保配电网安全运行，运行过程中支路电流不应越限，且节点电压应保持在安全范围内，因此对应的配电网安全运行约束条件为：

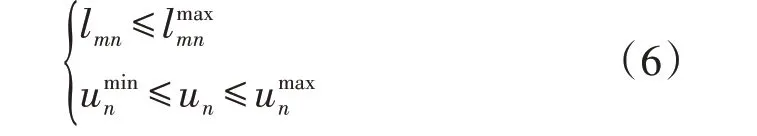
3）PV逆变器控制约束。

本文采用文献［14］中的PV 逆变器最优控制模型，该最优控制模式可对逆变器的有功、无功输出进行调节，其工作区域示意图如附录A 图A1所示。根据图A1所示的PV 逆变器工作区域，可得PV 的运行约束为：

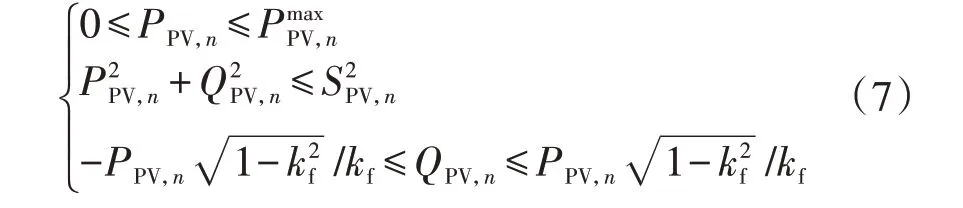
式中：QPV，n为节点nPV逆变器的无功输出功率；SPV，n为节点nPV 逆变器的额定容量；kf=cosθ，为PV 逆变器的最小功率因数，其为给定常数。易知，式（7）为凸约束。

显然，式（7）所示的约束充分考虑了PV 逆变器额定容量和最小功率因数的限制。以图A1 中的区域Ⅰ为例，PV 逆变器运行在边界0-1上时表示PV 仅有功输出可调，无功输出为0；运行在边界1-2 上时表示PV 仅无功输出可调，有功按最大功率输出；运行在边界2-3上时表示PV有功、无功输出均可调，但受逆变器额定容量限制；运行在边界3-0 上时表示PV 有功、无功输出均可调，但受最小功率因数限制。整个区域Ⅰ均满足PV逆变器的运行约束条件，且逆变器输出的无功功率为感性，故在该区域优化PV逆变器的功率输出，有利于低电压的提升。区域Ⅱ的运行边界与区域Ⅰ的运行边界约束相同，但区域Ⅱ内PV 逆变器输出容性无功，即消耗感性无功，故在该区域优化PV的功率输出，有利于过电压恢复。

1.2 模型的凸化处理

式（1）所示的非线性目标和式（2）所示的非凸非线性等式约束将导致所构建的模型非凸，进而难以获得模型最优解。为此，本节对上述模型进行凸化处理。为了将式（1）中非线性目标线性化，引入节点电压幅值与其平方的等式关系，如式（8）所示。进一步地，利用SOC 松弛技术对式（2）和式（8）进行凸化处理，分别如式（9）和式（10）所示。

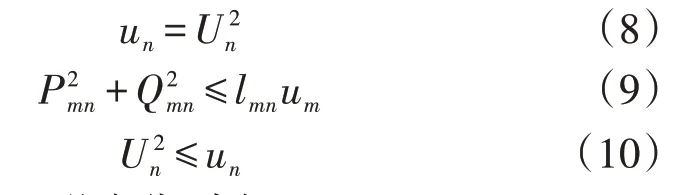
其标准的SOC形式分别为：

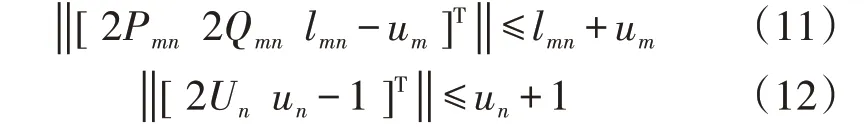
上述SOC 松弛过程如附录A 图A2 所示。利用SOC 松弛技术，可将原问题的非凸可行域Coriginal松弛成一个凸锥可行域CSOC，进而将原问题转化成了一个凸问题。由于引入了SOC 松弛，在CSOC中求解得到的最优解S是原问题的下界解，若最优解S为原始可行域Coriginal中的点，则SOC 松弛被认为是精确的，即最优解S也为原问题最优解。文献［15］严格推导了松弛精确成立的充分条件，在满足一定条件下，即目标函数为关于支路电流的增函数、网络拓扑为辐射形连通图等，证明了原问题在得到最优解时，可以保证松弛后的等号足够精确，满足原问题的所有约束。而本文所提主动配电网电压优化问题可以满足上述条件。由于松弛后为凸模型，采用传统的分支定界法和切平面法也可以保证解的最优性和计算效率。经凸化处理后，式（1）所示的模型可重新表述为：

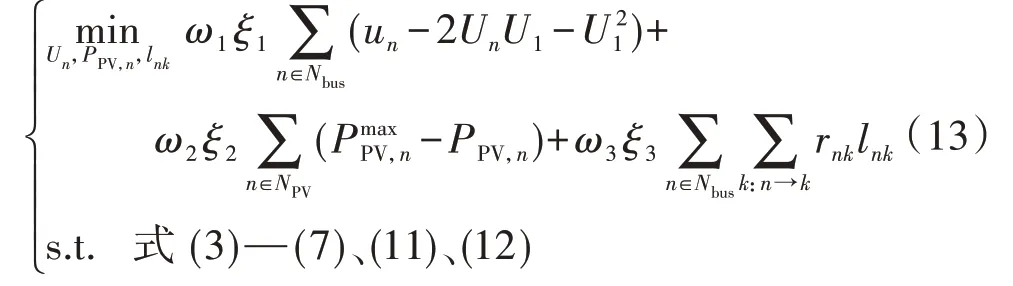
2 电压分布式优化控制模型及其求解

针对上述电压优化控制模型，一般可通过附录A 图A3 所示的集中式和分布式优化控制来实现全局最优控制。图A3（a）中，集中式优化控制将所有的PV 和负荷运行信息经过通信网络传送到中央控制中心，由中央控制器统一进行优化计算，并发布最优的控制指令，以实现控制的全局最优。然而，随着高比例分布式PV电源的接入，集中式优化控制存在通信网络建设成本高、计算复杂度大、信息私密性差且易出现单点故障等弊端［16］。分布式优化控制方法可以很好地克服上述问题，该控制模式如图A3（b）所示。PV 和负荷运行信息仅需上传到其所属子区控制中心，各子区控制器可独立、并行计算，相邻子区仅需交换少量边界信息，通过迭代计算实现全局最优，各子区独立发布最优控制指令。因此，本文采用分布式优化控制方法实现配电网电压的全局最优控制。

为此，本节首先基于分解协调原则将配电网分区，构建基于ADMM 的电压分布式优化控制模型；然后，基于残差平衡原理和松弛技术，提出一种加速ADMM 来改善算法收敛性能；最后，采用加速ADMM对电压分布式优化模型进行求解。

2.1 基于ADMM的电压分布式优化控制模型

为实现含分布式PV 的主动配电网电压分布式优化控制，首先根据分解协调原则［17］，将配电网分区；然后，基于ADMM 一般一致性优化方法［18］，建立电压分布式优化控制模型。

2.1.1 配电网分区

本节以图2所示6节点辐射形配电网为例，根据分解协调原则，对配电网进行分区。

图2 6节点辐射形配电网结构Fig.2 Structure of 6-bus radial distribution network

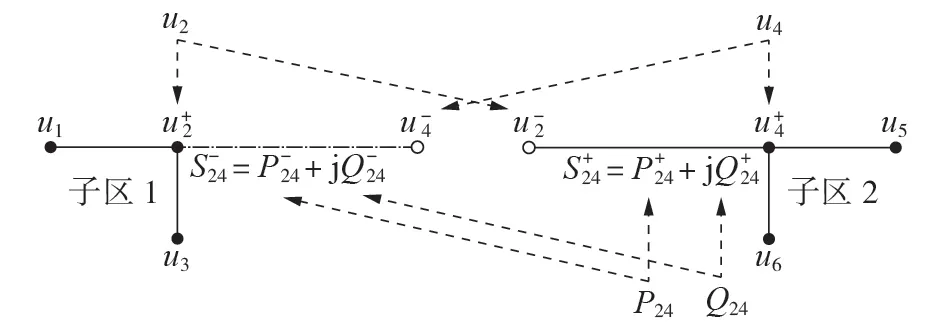
图3 6节点辐射形配电网分区过程Fig.3 Partition process of 6-bus radial distribution network

2.1.2 基于ADMM的分布式优化控制模型

ADMM 的思想是将凸问题中的原始变量分解为不同变量x和y，目标函数也分解为两部分，以保证优化过程的可分解性，算法标准形式如下：

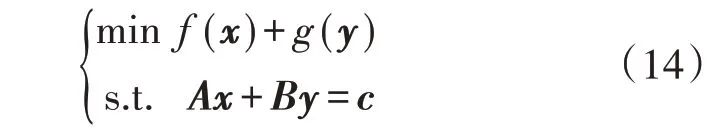
式中：f(x)和g(y)均为凸函数；A、B、c为系数矩阵。变量x和y的约束条件Ax+By=c构成了ADMM 目标函数中变量的可行域［19］。

基于文献［18］所提ADMM 的一般一致性优化方法，本文以式（14）中f(x)表示各子区独立优化目标，构建的基于ADMM 一般一致性优化方法的电压分布式优化控制模型为：

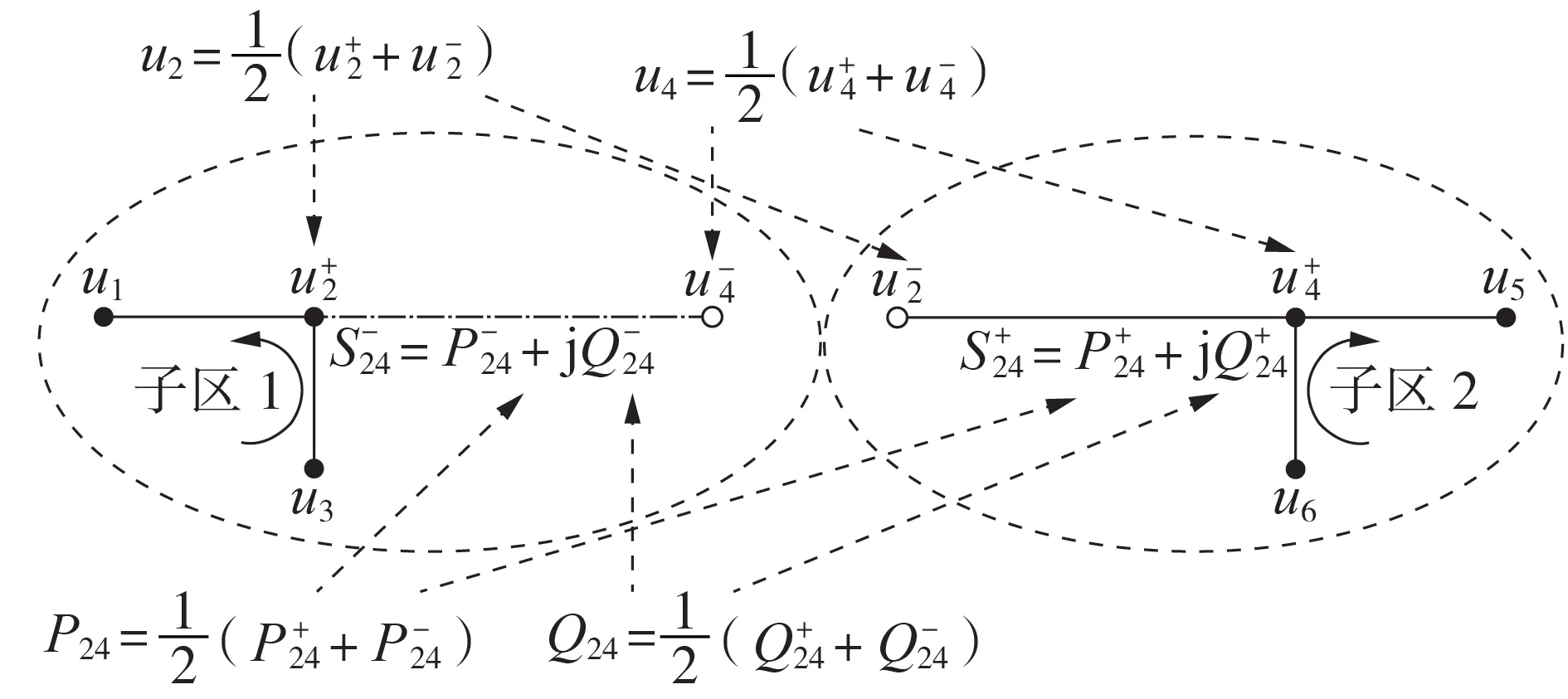
图4 子区独立优化和子区间的边界变量交互Fig.4 Independent optimization of sub-network and boundary variables exchange between sub-networks

2.2 加速ADMM

由于采用ADMM 求解所提电压分布式优化控制模型过程时，传统ADMM 的计算效率受惩罚参数影响严重且迭代次数过多，为此，本文基于残差平衡原理和松弛技术［18］，提出一种加速ADMM 来改善算法收敛性能，具体方法如下。

1）自适应惩罚参数。

由于惩罚参数选取不当将导致初始、对偶残差的收敛速度差别较大，迭代次数过多，故基于残差平衡原理，提出一种自适应惩罚参数方法，具体如下：

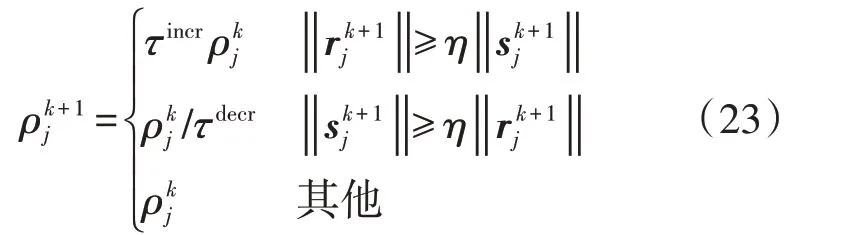
式中：η>1，τincr>1，τdecr>1，一般情况下，令η=10、τincr=τdecr=2。若增大ρj的数值，将增强式（16）和式（17）中范数项的最小化程度，促进子区边界变量x̂j与其全局变量ŷj相等，加快rk+1j收敛；若减小ρj的数值，可抑制目标函数振荡，加快ŷj的收敛。

2）超松弛。

在利用ADMM 迭代计算过程中，基于松弛技术引入松弛参数α∈(0，2)，若α>1 则为超松弛；在ŷ和μ的更新公式中，计及上一次迭代计算结果，用αAxk+1-(1-α)(By-c)代替Axk+1，有助于数值平稳更新。经整理，迭代计算过程如下：

2.3 基于加速ADMM的模型求解

综上，本文利用所提加速ADMM 求解含分布式PV 的主动配电网电压分布式优化控制的计算流程如附录A图A4所示，相关计算过程如下。

4）由式（21）计算初始残差rj和对偶残差sj，并利用式（22）判断是否收敛，若初始、对偶残差均小于收敛阈值，则停止迭代并输出电压优化控制结果；否则，根据式（23），利用自适应惩罚参数方法，更新惩罚参数ρj并返回到步骤3）。

3 算例分析

针对所提含分布式PV 的主动配电网电压分布式优化控制方法，本节通过含分布式PV 的IEEE 33节点测试系统进行算例分析，以验证所提模型的可行性和算法的有效性。

IEEE 33 节点测试系统如图5 所示。分布式PV编号为PV1—PV9，依次安装在节点5、8、11、15、18、21、25、29 和33，最小功率因数kf=0.95；基于文献［19］提出的利用系统分区形成的全局变量数量来指导系统分区的方法，综合考虑配电网络拓扑结构、地理区域和PV 分布等情况，以节点5、6 和支路5-6 为边界分解子区A1和A2，以节点8、9和支路8-9为边界分解子区A2和A3；子区A1—A3安装的分布式PV电源分别为（PV1，PV6，PV7）、（PV2，PV8，PV9）和（PV3，PV4，PV5）。在本文算例中，令电压基准值为12.66 kV，基准负荷为3 715+j2 300 kV·A，功率基准值为10 MW，节点电压安全运行范围为［0.95，1.05］p.u.。

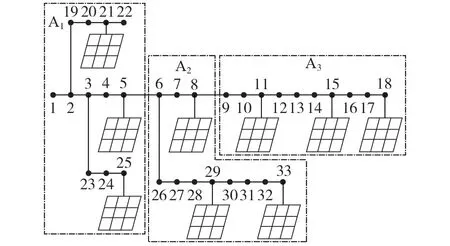
图5 IEEE 33节点测试系统示意图Fig.5 Schematic diagram of IEEE 33-bus test system

3.1 电压优化控制前后对系统运行的影响

为研究所提电压优化控制策略对配电网电压、PV 削减量和网损的影响，分别设置以下2 种场景：场景1 为PV 出力大且负荷水平低导致系统节点电压出现越上限的情景；场景2 为PV 出力小且负荷水平高导致系统节点电压出现越下限的情景。

上述2 种场景下式（1）中各权重系数取值为ω1=0.4，ω2=0.3，ω3=0.3，各场景的计算结果说明如下。

1）场景1。

晴朗天气下，在10:00—14:00间的某一时刻，光照充足且负荷水平低，造成PV 出力过剩，从而导致部分节点电压越限，此时PV输出功率如附录B表B1中控制前的输出功率所示，负荷为基准负荷的50%。采用所提控制策略对分布式PV 进行有功、无功调节，优化控制前、后系统节点电压分布如图6 所示。图中，节点电压为标幺值，后同。

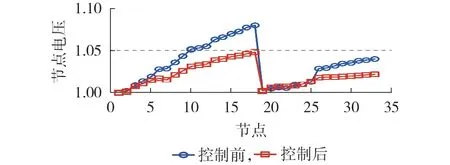
图6 场景1下控制前、后系统节点电压分布Fig.6 Node voltage profiles of system before and after control in Scenario 1

图6 中，优化控制前由于PV 出力过剩，导致节点10—18 电压出现了越上限现象，其中节点18 电压越限至1.08 p.u.。为使配电网节点电压均在安全运行范围内，采用所提电压优化控制策略后PV输出功率及其变化量如附录B表B1中控制后的输出功率所示，其中正值表示PV增发有功／感性无功，负值表示削减有功／发出容性无功。根据本文所提算法可得PV2—PV5、PV8和PV9均发出容性无功，用于抑制节点电压的升高；由于节点18 电压越限最为严重，PV5需削减64 kW 有功输出来弥补无功调节的不足，进而满足电压控制要求。通过对PV有功、无功输出进行调节，系统各节点电压均运行在1～1.0479 p.u.之间，满足电压安全约束。同时，由于PV1、PV6和PV7的无功调节对电压越限节点的影响小，故其发出感性无功主要用于优化系统潮流分布，补偿无功负荷，以减小网损。然而，为消除电压越限，PV增发的容性无功将导致系统净无功负荷增加了641 kvar，进而导致网损增大了54.8 kW。

2）场景2。

选择傍晚（17:00—19:00）的某一时刻，此时光照强度下降、负荷增大，导致部分末端节点电压越下限，PV 输出功率为附录B 表B2 中控制前的输出功率，负荷为基准负荷的1.2倍。采用本文所提方法对分布式PV 控制前、后的配电网节点电压分布如图7所示。

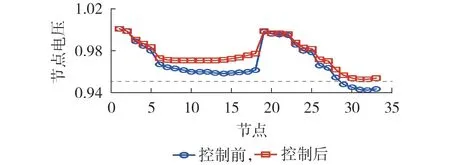
图7 场景2下控制前、后系统节点电压分布Fig.7 Node voltage profiles of system before and after control in Scenario 2

图7 中，由于PV 出力变小且负荷增加，电压优化控制前，系统节点电压水平较低且末端节点29—33 电压低于下限值，如节点32 电压低至0.942 p.u.。采用所提优化控制策略后PV 输出功率及其变化量如附录B 表B2 中控制后的输出功率所示。此时，PV1—PV9有功输出变化量均为0，即系统PV 有功输出未发生变化，各PV 无功输出受最小功率因数限制，充分利用PV逆变器无功输出能力增发感性无功789 kvar 以减小系统净无功负荷，进而提高系统节点电压水平，系统节点电压运行在0.952 1～1 p.u.之间，网损减小了45.7 kW。

场景1、2的分析结果表明：采用本文所提含分布式PV 的主动配电网电压分布式优化控制策略可有效解决配电网电压越限问题。场景1 下，PV 通过增发容性无功和适当削减有功，可消除电压越上限的现象；场景2 下，PV 通过增发感性无功补偿无功负荷，可消除电压越下限的现象，同时可减小网损。因此，通过调节分布式PV的有功、无功输出，有助于改善系统电压安全性，使系统运行更安全、经济。

3.2 权重系数对系统运行的影响

由式（1）可知，不同的权重系数ω1—ω3将直接影响所提电压分布式优化控制策略的结果，为此本节进一步研究了不同ω1—ω3取值对系统电压、PV削减量和网损的影响。由于减小单位网损可能导致削减更多的PV，故在本节算例中仅研究权重系数对电压偏差和PV 削减量的影响。令ω1+ω2=1，ω3为十分接近于0 的数值，用于保证SOC 松弛后原问题的精确性，可忽略其对电压偏差和PV削减量的影响。设置以下5种不同的权重系数(ω1，ω2)组合：G1=（1，0）、G2=（0.75，0.25）、G3=（0.5，0.5）、G4=（0.25，0.75）和G5=（0，1），这5 种组合代表了目标函数从完全最小化电压偏差到完全最小化PV削减量的变化。

图8 为不同权重系数下节点电压分布情况。不难看出，随着电压偏差最小化权重系数的减小，组合G1—G5的系统节点最大电压偏差逐渐增大，由0.0005 p.u.增大到0.05 p.u.。

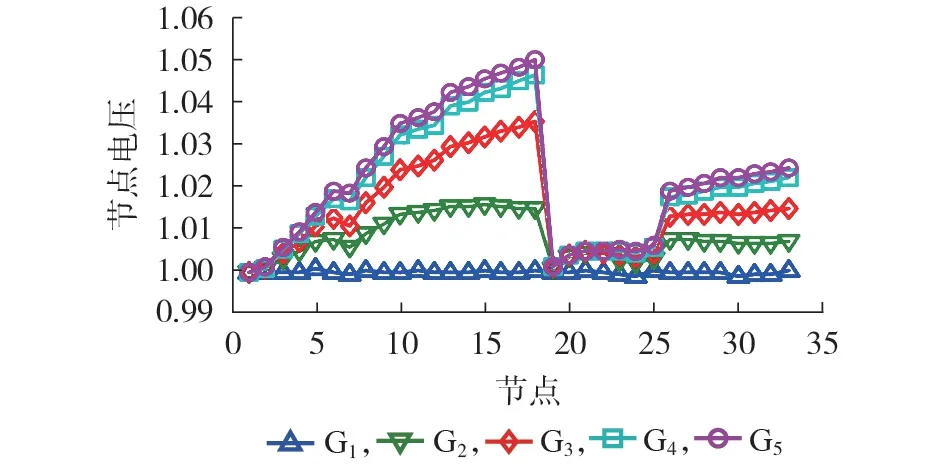
图8 不同权重系数下节点电压计算结果Fig.8 Calculation results of node voltage with different weight coefficients

不同权重系数下的PV 功率输出情况如附录B 图B1 所示。图B1（a）为PV 电源有功输出情况，随着PV 削减量最小化权重系数的增大，组合G1—G5的系统总PV 有功输出由1 966.3 kW 逐渐增大到4 479.9 kW；在组合G2中，电压偏差最小项影响仍较大，PV5位于系统末端且距根节点1 最远，其有功出力增加不利于电压分布，为了增大系统PV电源有功出力，同时保持较好的电压分布，此时削减了PV5的有功输出。图B1（b）为PV 电源无功输出情况，由于组合G1完全最小化电压偏差，此时PV 电源发出的感性无功用于补偿系统无功负荷，以减小电压偏差；然而，在组合G2—G4中，最优潮流下，PV 电源发出容性无功来抑制电压的升高，同时随着电压偏差最小化影响程度的下降，发出的无功逐渐减小；在组合G5中，由于完全最小化PV削减量，部分PV电源发出感性无功用于减小网损。

表1 为不同权重系数下系统的PV 削减量、网损和功率损失，其中功率损失为PV 削减量和网损之和。可见随着PV 削减量最小化程度增加，PV 削减量和系统功率损失逐渐减小，由于电压偏差和PV削减量存在最小化的平衡过程，网损呈现先增加后减小的趋势。

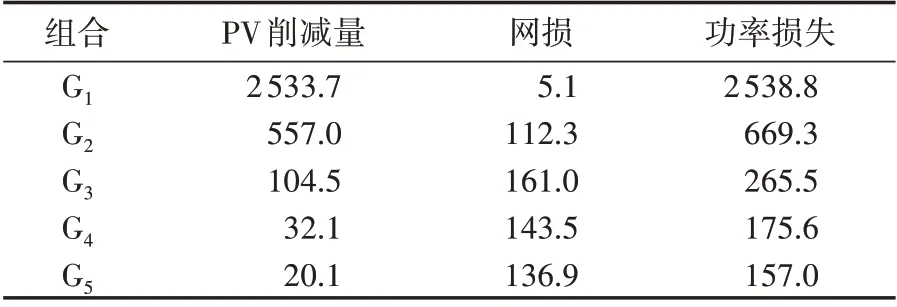
表1 不同权重系数下系统的PV削减量、网损和功率损失Table 1 PV curtailment，network loss and power loss of system with different weight coefficients单位：kW

上述分析表明：调整权重系数可实现不同的优化方案，组合G1实现了电压偏差最小，有利于系统的安全运行；组合G5实现了PV 削减量最小，同时系统功率损失最小，使系统运行更经济。因此，改变优化模型中的权重系数，可有效权衡电压偏差与PV削减量间的最小化程度，使配电网运行更加主动、灵活。

3.3 基于加速ADMM的分布式优化方法分析

本节首先对比了3.1 节中场景1 和3.2 节中组合G3的分布式优化结果与集中式优化结果，以验证所提电压分布式优化方法的可行性；然后，分析了所提模型SOC松弛的精确性，以验证该模型的有效性；最后，对本文采用的加速ADMM 收敛性能进行分析、验证。

表2 为场景1 和组合G3下分布式与集中式优化结果的数值对比，表中电压偏差为标幺值。不难看出，采用分布式优化后的系统节点电压偏差、PV 削减量和网损与集中式优化结果十分接近，偏差均在合理范围内，故利用所提方法可实现配电网电压全局最优控制；同时，分布式优化计算效率高于集中式。由此可得，采用所提分布式优化方法可通过交换少量边界信息实现系统全局最优控制，且计算效率高，能适应含分布式PV的主动配电网运行需求。

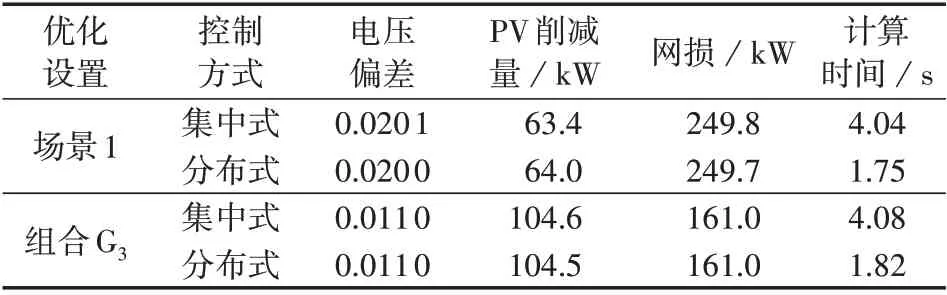
表2 分布式与集中式优化结果对比Table 2 Comparison of results between distributed and centralized optimization

为验证所提电压分布式优化中SOC松弛的精确性，由式（25）定量计算了场景1、2 和组合G1—G5的节点电压和支路电流的SOC 松弛间隙最大值δu，SOC和δl，SOC。各分布式优化中SOC 松弛间隙最大值如附录B 表B3 所示。由表可知，各分布式优化中节点电压SOC 松弛间隙最大值均小于10-7p.u.，支路电流SOC 松弛间隙最大值均小于10-5p.u.，满足松弛后原问题的精确性要求，因此可认为所提电压分布式优化模型的计算结果是原非凸问题的全局最优解。

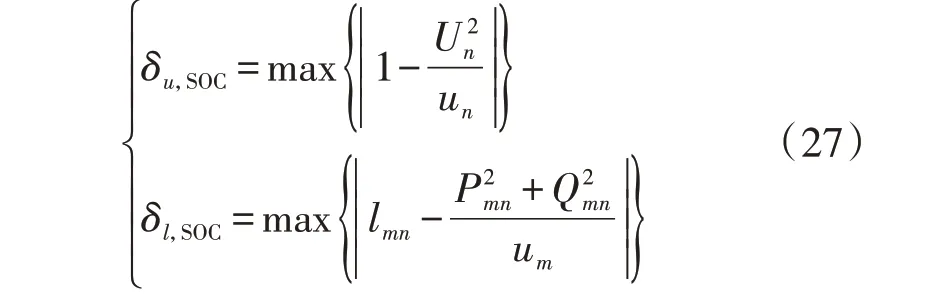
图9为利用传统ADMM 和加速ADMM 求解时目标函数值（标幺值）的收敛过程。不难发现：利用加速ADMM 进行求解时，目标函数可快速收敛到与集中式优化结果十分接近的数值。传统ADMM 收敛所需的迭代次数为107 次，计算耗时为3.77 s；而本文所提的加速ADMM 所需迭代次数仅为42次，计算耗时为1.73 s，是传统ADMM 计算耗时的0.46。由此可得，本文所提加速ADMM 具有良好的收敛性能，可有效减少迭代次数，提高算法计算效率。

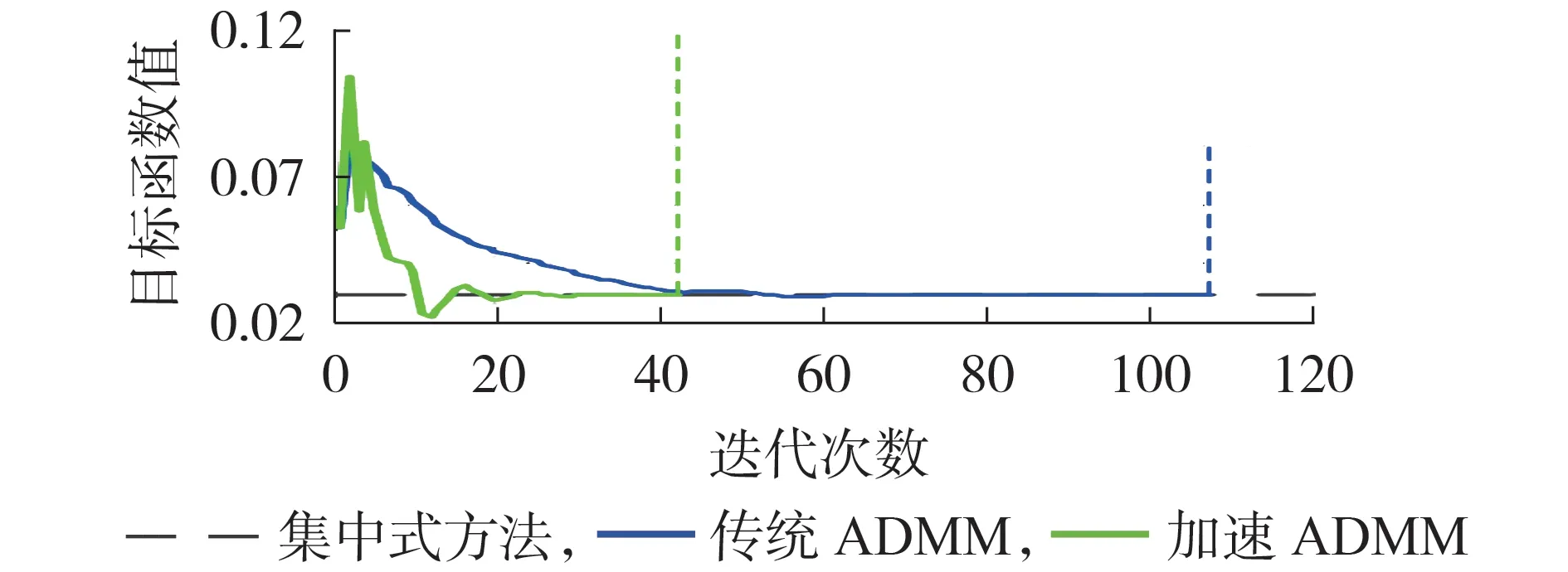
图9 目标函数值的收敛过程Fig.9 Convergence process of objective function value

不同惩罚参数下的算法收敛性能如附录B 表B4 所示。可以看出：不同惩罚参数下，加速ADMM的收敛迭代次数和计算时间均小于传统ADMM；同时，所提加速ADMM 可有效降低算法收敛性能对惩罚参数的敏感性。当惩罚参数ρ取值在［4，32］之间时，加速ADMM 的收敛迭代次数和计算时间变化不大；当ρ=64 时，加速ADMM 迭代77 次可自动收敛，而传统ADMM 达到最大迭代次数时才停止收敛。由此可知，所提加速ADMM 可有效解决由惩罚参数选取不当导致算法收敛困难的问题。