无应力原长的覆冰输电线路找形研究

谢东升，孙 滔，史卓鹏，智生龙，白天明，李海涛

(1.国网山西省电力公司经济技术研究院， 太原 030002； 2.中北大学 理学院，太原 030051)

输电线路覆冰是威胁电网安全运行的主要隐患之一，覆冰输电线在风力作用下的舞动以及覆冰脱落所引起的线路振荡，可能导致相间闪络、金具损坏、断线倒塔等安全事故，因此分析覆冰输电线路的力学特性对于线路的安全运行具有重要意义[1-5]。在输电线路静动态力学分析中，确定输电线的初始平衡状态，即找形分析，是后续计算的前提和基础，找形结果的准确性对后续力学分析的精度有重要的影响[6-9]。

由于输电线路档距远大于输电线截面直径，输电线的刚度对其悬挂曲线的几何形状影响较小，可将输电线假设为柔性悬索，因此确定输电线的初始平衡状态属于索的找形问题[10]。该问题的分析方法主要有力密度法、动力松弛法和非线性有限元法[11]，其中非线性有限元法在我国应用较为广泛。

当前，输电线找形的有限元方法主要分为3类：直接迭代法[12-15]是以输电线弦线位置创建模型，采用实际材料性质和实常数，并设置很小的初应变，然后施加载荷，以输电线水平张力为收敛条件进行迭代计算，收敛后获得输电线初始构形；小弹性模量法[16-20]在建立输电线弦线模型时设置较大的初应变和较小的弹性模量，求得输电线在载荷作用下的初始线形，然后恢复实际弹性模量进行非线性迭代，当水平张力满足收敛条件时即得到输电线的初始构型；V形折线法[21-22]是以找形后输电线线长来建立V形折线模型，设置实际弹性模量，施加载荷以及初始应力进行非线性迭代，得到最终悬链线形态。

3种方法中，直接迭代法设置简单、操作方便，但需大量迭代才能收敛；小弹性模量法在得到初始线形后还需二次导入线形进行自平衡求解，且预设的弹性模量值需多次尝试，迭代计算可能会出现不收敛的情况。相比前2种方法，V形折线法根据输电线线长设置了合理的初始模型，提高了计算效率和可靠性，但对于两端有高差情况求取中间节点计算较繁琐。

针对上述方法存在的不足，提出了基于无应力原长[23]的输电线找形方法。本方法初始模型为输电线弦线且给出了较强的初值条件，在保证计算精度的前提下具有收敛速度快、设置简单的优点。进一步，结合覆冰前后输电线形态的实际测量结果，对比分析了几种找形方法的精度，验证了本方法的准确性。

1 找形原理及步骤

本找形方法的主要分析步骤包括：① 根据档距、比载及观测的弧垂计算得到输电线的悬链线长度以及输电线在载荷作用下的变形量，从而可确定输电线无载荷作用时的长度，即无应力原长；② 比较输电线挂点弦线长度与无应力原长，将两者的长度差等效为温度变化所引起的伸缩量，并根据导线热膨胀系数计算相应的温度变化量；③ 将挂点间的弦线作为输电线找形前的有限元模型，在重力载荷及等效温度变化作用下平衡即得到输电线最终形态。

1.1 输电线无应力原长计算

单档输电线理论计算的基本假设为：① 输电线为理想柔性悬索，仅能承受拉力而不能承受弯矩和压力；② 输电线材料特性符合胡克定律；③ 输电线的竖直载荷沿弧线均匀分布[24]。根据上述假设，由输电线的平衡条件可得到架空输电线空间曲线形状为悬链线，如图1所示。

图1 输电线初始形态示意图

若选取输电线最低点O为坐标原点，载荷沿线长均匀分布， 则可得到架空输电线的悬链线方程(1)和任意点M的应力公式(2)[24]：

(1)

(2)

式中：γ为输电线比载；σO为输电线在比载γ作用下的水平应力。

若在输电线上M处取微段(图2)，则微段长度dL及由应力作用所引起的弹性变形量dΔL可分别表示为：

图2 M点处输电线微元

(3)

(4)

式中，E为输电线弹性模量。

则微段无应力作用时的长度dL0为dL与dΔL之差，由式(3)(4)可表示为：

(5)

将式(5)在输电线全档内进行积分，由式(1)(2)可将输电线无应力原长L0表示为：

(6)

其中：a、b为输电线挂点横坐标：

(7)

(8)

式中：l为输电线档距；h为输电线两端悬挂点的高差。

对线路进行找形分析时，可先由观测得到的输电线最大弧垂或跨中弧垂计算得到水平应力σO[25]，再由式(6)计算得到输电线无应力原长L0。

1.2 等效温度变化量和等效比载计算

为将输电线挂点间弦线作为找形初始几何模型，比较输电线无应力原长L0和弦线长度Ls，将两者之差等效为由于温度变化所引起的输电线伸缩量，若输电线热膨胀系数为α，则等效温度变化量Δt可表示为：

(9)

进一步，将均匀分布在输电线上的载荷等效到输电线弦线上，由输电线比载γ可计算得到弦线等效比载γ1：

(10)

计算得到等效温度变化量Δt和等效比载γ1后，可根据输电线悬挂点坐标建立弦线有限元模型，进而施加等效温度变化量Δt和等效比载γ1进行平衡状态求解即可完成输电线找形。

1.3 有限元找形流程

针对输电线只能受拉不能受压的特性，在ABAQUS中采用T3D2单元进行模拟，并设置材料为不可压缩。根据输电线两侧挂点位置建立弦线模型，赋予材料属性，设置约束条件，施加计算得到的等效比载及等效温度变化量进行迭代求解，收敛后就得到了输电线载荷作用下的初始构型。当考虑覆冰问题时，将覆冰载荷叠加至线路自重比载即可。无应力原长法找形流程如图3所示。

图3 找形流程框图

2 覆冰线路现场观测

为验证找形方法的准确性，对山西省忻州地区某220 kV退役线路某档段进行了现场观测，测量得到了输电线覆冰前后的弧垂和张力信息，为分析找形方法的准确性提供了现场实验数据。

2.1 线路简介及观测方法

观测线路为忻州地区220 kV平凤线39#-40#档段， 39#塔为直线塔，40#塔为耐张塔，档距约为104 m。导线型号为LGJ-300/40，参数如表1所示，自左向右依次标记为导线A、B和C，如图4(a)所示。观测线路所在地区为典型的微地形、微气象覆冰区，2019年12月15至16日由于该地区出现雨雪天气，使观测线路上形成覆冰。覆冰形成后，在临近观冰站对同型号导线覆冰厚度和密度进行测量，得到导线平均覆冰厚度约30 mm，密度约为0.2 g/cm3，为典型北方常发性雾凇覆冰，如图4(b)和4(c)所示。

表1 LGJ-300/40型号导线机械参数

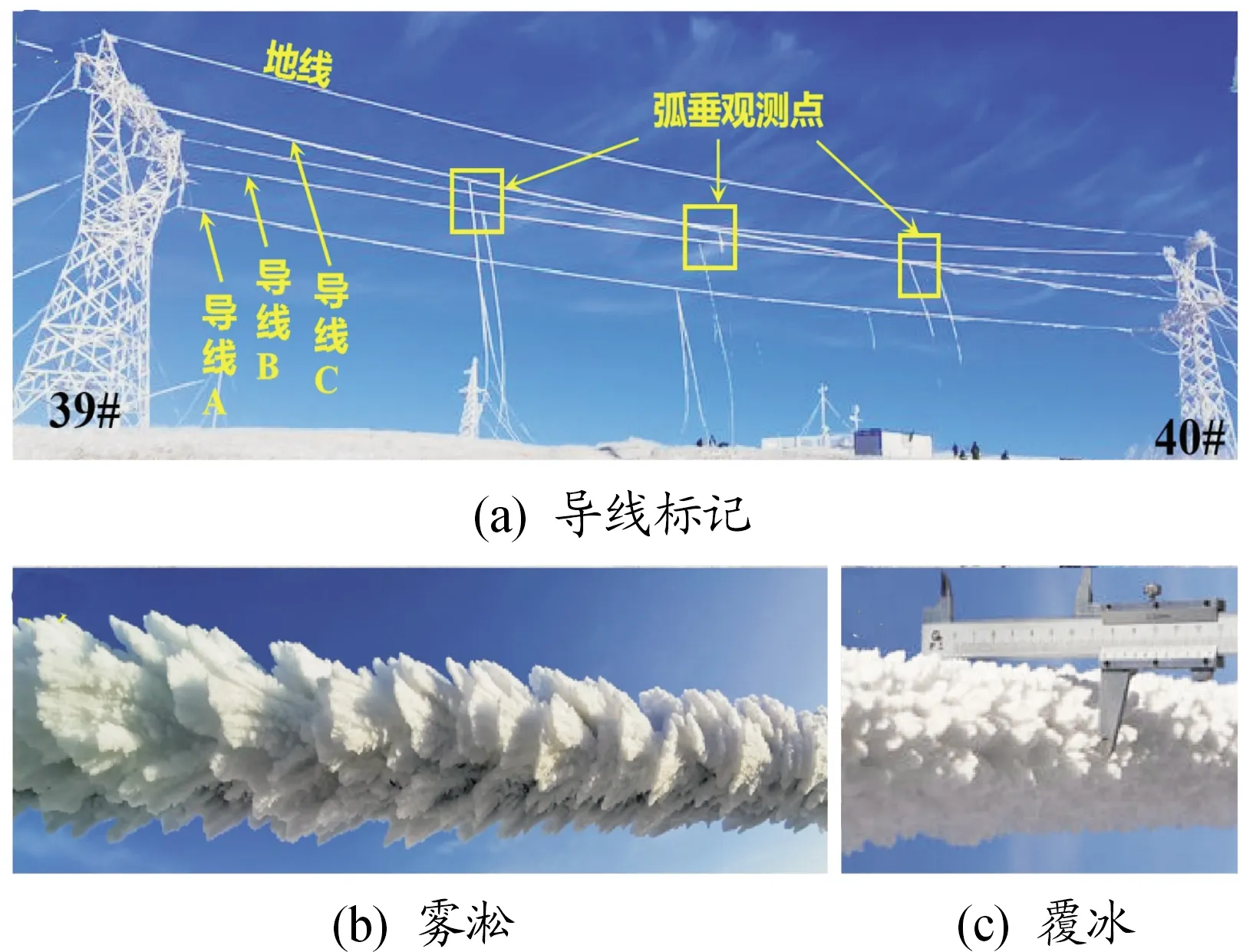
图4 覆冰线路观测景像图

为确定覆冰前后导线形态，覆冰前在每根导线上作10个标记点，采用全站仪(KTS- 442R8，如图5(a)所示)观测覆冰前后输电线两侧挂点及标记点的坐标并计算导线弧垂。为监测覆冰前后导线张力变化，在各导线直线塔一侧近绝缘子串处安装表面应变计式力传感器(EY501，如图5(b)和5(c)所示)，采用DH3820应变测试分析系统采集并输出覆冰前后导线端部张力的变化量，如图5(d)所示。覆冰前，观测得到导线A和C左右两侧挂点高差约+7 m，导线B挂点高差约+3 m，3根导线挂点间弦线长度依次为104.75、103.68、103.94 m；线路覆冰后，观测得到悬垂绝缘子串由覆冰引起的偏转较小，可认为覆冰后各导线挂点间弦线长度与覆冰前相同。

2.2 观测结果

表2给出了覆冰前后3根导线跨中弧垂w和端部张力差ΔF的测量结果。另外，根据导线弧垂测量结果可理论计算出各导线覆冰前直线塔一侧挂点张力分别为14.507、10.652、11.788 kN。由结果可知：覆冰后导线跨中弧垂分别增大约86.4%、54.3%和71.2%，端部张力相对于其覆冰前理论预测值分别增大约57.8%、77.8%和80.3%。可知覆冰引起的导线弧垂和张力的变化量较大且与导线预应力、初始形态以及覆冰厚度等因素相关，因此在架设导线时应充分考虑并预测覆冰量以保障其安全性设计。

(a)全站仪; (b)表面应变计安装方式; (c)表面应变计; (d)应变仪

表2 覆冰前后导线的端部张力差和跨中弧垂

3 找形结果分析与讨论

3.1 覆冰前后导线找形结果分析

基于覆冰前观测的导线跨中弧垂，采用本文方法分别计算各导线从无应力原长变化至对应的挂点弦线长度所需的等效温度变化量Δt分别为：27.97、10.61、16.40 ℃。然后，以导线A为例，建立有限元模型，如图6(a)中虚线所示。对模型施加等效重力比载γ1和等效温度变化量Δt，计算可得无覆冰时导线自重作用下的构型，如图6(a)中实线所示，而导线任意位置弧垂大小由彩色等值线标识，可知最大弧垂位于导线中点附近区域。然后，通过变化等效比载即可获得覆冰工况下对应的导线构型和竖直方向位移场。图6(b)为导线覆冰前后应力场，其中实线为导线形态，虚线为对应位置处应力幅值。分析可知，由于覆冰前导线两端应力差值主要由高差引起，因此应力自左向右变化较小。覆冰后，导线两端应力差有所增大，但应力差值约为平均应力的1.0%，覆冰前后应力基本可认为均匀分布。但是当导线两端高差较大时，由覆冰引起的张力不平衡也会随之增大，需要采取对应措施。

图6 覆冰前后竖向位移和应力场云图

采用相同方法对其余两根导线进行找形分析，对比导线覆冰前后导线跨中弧垂和端部张力的观测和模拟结果，如表3所示。需要指出的是，由于实验中无法测量端部张力的绝对值，仅能够测量覆冰前后张力的变化量，因此表内观测项内覆冰前后张力数据均为理论预测值。

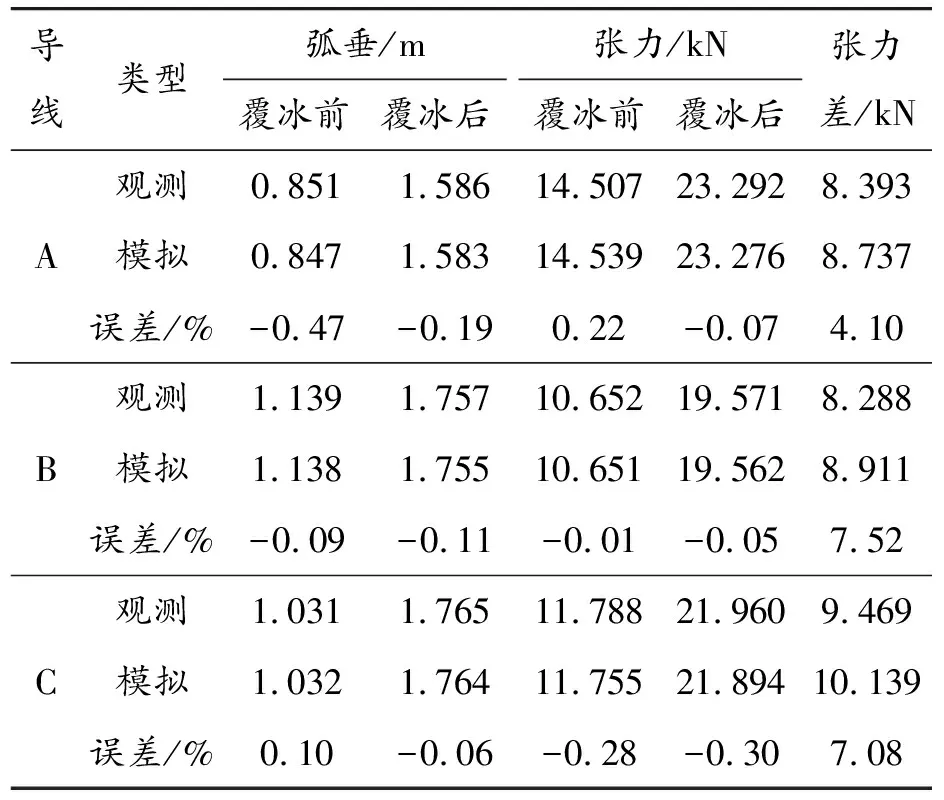
表3 弧垂与端部张力的观测值与找形结果对比

由对比结果可知：基于本文提供找形方法构建的有限元模型能够较为准确地预测导线覆冰前后弧垂和端部张力，其预测结果与观测/理论值误差绝对值不大于1%。然而，测得的覆冰前后张力变化值与模拟结果之间的偏差约为5%～7.5%。分析认为测量误差为主要原因：一方面，应变式传感器通过附加装置与导线间的连接并非理想固连条件，固定装置随导线舞动过程中的松动等原因可能造成测量误差；另一方面，钢芯铝绞线并非均匀材质的杆件，以等效弹性模量计算载荷时可能引入误差。另外，研究结果表明档距较小时，导线的刚度、线路两端的金具以及余长等均可能导致载荷的计算出现误差[26]。然而，测量结果与理论值偏差10%以内时，仍可为工程问题提供有效参考。

图7为3根导线覆冰后标记点处竖向位置的观测结果与找形结果。

图7 覆冰后标记点位置的观测值与找形结果曲线

由图7可知，基于所提出方法开展的找形分析在预测导线形态时，也可提供较为准确的结果，局部位置实验与模拟结果的偏差可能由于实际覆冰并不均匀所致。综上可知，基于所提出的方法找形结果精度较高，所得弧垂和张力与实际结果误差足以满足工程需求，验证了本找形方法的准确性。

3.2 找形方法评价

当前研究认为，针对输电线找形，直接迭代法是操作最简便、应用最广泛的方法，而小弹性模量法则精度较高。基于导线现场观测数据，对比分析了本文方法与直接迭代法[13]、小弹性模量法[17]的找形结果。其中，3种方法得到的跨中弧垂以及实验观测值与悬链线解的相对误差如图8(a)所示，端部张力与悬链线解的相对误差如图8(b)所示。

图8 不同找形方法误差分析图

由图8可知：3种方法找形后的跨中弧垂和端部张力与理论值的误差均小于±0.7%，能够满足工程的实际需要。其中，小弹性模量法精度最高，本文方法在跨中弧垂预测方面与直接迭代法精度相近，但端部张力的计算精度高于直接迭代法。对比可知，所提出的找形方法计算效率和精度高于直接迭代法，但需事先对输电线路的原长进行数值求解以预置有限元分析参数，而与小弹性模量法相比无需二次导入模型，简化了分析步骤，缩短了计算时长，可为输电线路找形分析提供一种新的思路。

4 结论

1) 档距为104 m的LGJ-300/40导线在30 mm雾凇覆冰下，跨中弧垂增加54%～71%，对应端部张力增加57%～80%，覆冰区输电线路强度设计时应予以考虑。

2) 所设计的无应力原长法能够较为准确地预测输电线覆冰前后形态、弧垂以及张力等关键参数，能够满足工程需要。

3) 无应力原长法的精度和计算效率优于直接迭代法，与小弹性模量法相比找形设置更为简便。