基于信息熵与改进极限学习机的中长期径流预测

2021-09-14岳兆新熊传圣宋艳红于家瑞

水利水电科技进展 2021年4期

岳兆新，艾萍，熊传圣，宋艳红，洪敏，于家瑞

(1.河海大学计算机与信息学院，江苏南京 211100； 2.南京工业职业技术大学计算机与软件学院，江苏南京 210023；3.河海大学水文水资源学院，江苏南京 210098)

水文中长期预报是指基于水文现象演化的客观规律，根据前期和历史水文、气象等信息，运用成因分析和数学建模等方法，对未来较长时间内水文情势做出定性或定量预报[1-2]。及时、准确的中长期水文预报可为水资源高效利用、水利工程建设与运行，以及防汛抗旱指挥决策等提供重要的基础数据和科学的决策依据。当前，中长期水文预报仍然处于探索、发展阶段，预报精度还不能满足各生产部门的实际需求。中长期径流预测是中长期水文预报中的一个重要研究方向，也是水信息学科研究与应用的重要难题之一。

目前，常用的中长期径流预测方法主要有成因分析方法、统计学方法、基于智能算法的预测方法和基于数值天气预报的预测方法四大类。其中，成因分析方法[3]和统计学方法[4-5]是水文学科的典型方法，具有一定的适用范畴，但也存在诸多需要研究的问题。比如影响径流序列长期变化的物理成因复杂，难以完全掌握其客观规律。而统计学方法多以线性方法为主，难以适应径流变化影响要素的复杂非线性特性，具有一定的局限性。基于智能算法和数值天气预报的综合预测方法是近些年发展起来的新方法，是伴随计算机信息技术的发展和新数学建模方法的涌现而发展起来的新技术。前者具有较好的非线性映射、泛化和容错能力，被广泛应用于径流预测领域[6-7]；后者则在水文预报中耦合一定预见期内的数值天气预报产品，在探索增长径流预报预见期方面，具有一定的研究意义[8]。基于智能算法的中长期径流预测模型主要根据输入输出变量之间的函数关系构建基于人工神经网络、支持向量机 (support vector machine, SVM)、小波分析等预测模型或者综合采用多个模型对未来中长期径流进行预测分析，并取得了诸多成果[9-13]。尽管上述基于智能算法的预测模型应用广泛，但模型结构相对复杂，参数在训练过程中需要初始化以及不断优化调整，效率相对较低，且 BP神经网络 (backpropagation neural networks, BPNN)采用基于梯度下降的方法，容易陷入局部最小值问题，算法需要多次迭代，因而整体效率不高。极限学习机[14](extreme learning machine, ELM)是一种单隐层前馈神经网络，具有参数设置简单、计算速度快、误差小、泛化能力强等优点，被广泛应用于故障诊断、图像处理等领域。

此外，影响径流过程变化的关键因子筛选也是中长期径流预测需要研究的重要内容。因子筛选方法主要包括先验知识法、相关系数法、主成分分析法和信息熵法[15-17]。先验知识法主要依赖于人工经验，主观性较强，具有一定的局限性。相关系数法和主成分分析法，整体上属于线性方法，难以适应中长期径流过程影响因子的复杂非线性特性，具有一定的适用范围。信息熵法，尤其是互信息方法忽略了变量分布，适用于备选因子间的线性和非线性相关关系。偏互信息方法是在互信息方法基础上的改进，可以有效避免对已入选因子的影响，减少冗余变量，降低计算复杂度。

鉴于此，本文提出一种基于信息熵与改进极限学习机的中长期径流预测方法。首先，基于不同水文站点的流域控制面积构造径流综合指数，在较宏观层面表征流域水情丰枯变化；其次，采用偏互信息方法计算影响对象与径流综合指数之间的相关性，获得径流过程变化的关键因子集，形成预测模型的输入；最后，结合K折交叉验证与改进粒子群算法优化ELM参数，构建IPSO-ELM(improved particle swarm optimization, IPSO-ELM)模型，用于中长期径流预测。

1 基于信息熵与改进极限学习机的中长期径流预测方法

1.1 径流综合指数构造

粒计算作为人工智能研究领域中的一种新理念方法，其目的是在问题的求解过程中，用粒度合适的“粒”作为处理对象，从而在保证求得满意解的前提下，提高解决问题的效率[18]。当前中长期径流预测，主要基于流域内某些典型站点(单一粒度)的径流变化来预测中长期径流变化情势，并没有结合研究区域内多个水文时空对象进行多粒度综合分析，导致复杂环境下流域中长期径流预测的宏观研判能力不足。因此，本文依据粒计算理论，通过研究分析流域中不同水文站点(细粒度)月平均径流的一致性，构造描述流域月均径流丰枯情况的流域径流综合指数(粗粒度)，在较宏观的层面研究整个流域的径流变化情势，以提高流域中长期径流预测的准确性和可靠性。以此为基础，本文通过研究流域内多个不同水文站点月平均径流的一致性，构造具有多粒度特性的流域径流综合指数(comprehensive runoff index, COM)，以表征流域径流的丰枯情况。为了避免测站之间的累积影响，更客观地使用各测站描述流域径流丰枯情况，本文在确定所选水文站点的权重时，采用削减流域下游水文站对整体指数的贡献度原则，基于站点流域控制面积构建流域径流综合指数。

假设流域站点数量为nS,第i个水文站的控制面积百分比为Si,第i个水文站，第j个月的月平均径流为cij，则第i个水文站的权重wi和第j个月的径流综合指数cj分别为

(1)

(2)

1.2 基于信息熵的因子筛选

互信息(mutual information, MI)以信息熵理论为基础，既能够度量输入变量与预测对象间的线性和非线性关系，也能够度量一个变量中含有的关于另一个变量的信息量[19]。但采用MI对输入变量进行筛选时，由于输入变量之间的耦合关系会对MI的计算结果产生影响，从而导致误选或漏选。因此，May等[20-21]提出了偏互信息法(partial mutual information, PMI)，通过计算条件期望消除了变量之间的联系，从而保证了变量选择的可靠性和准确性。偏互信息定义为

(3)

x′=x-E[x|z]

(4)

y′=y-E[y|z]

(5)

式中：E为期望值；x为备选输入因子；y为预测对象。

给定N个离散样本，偏互信息可采用如下离散形式定义：

(6)

1.3 IPSO-ELM预测模型构建

1.3.1极限学习机

假设给定任意N个不同样本(Xi,ti)。其中，Xi=(xi1,xi2,…,xin)T∈Rn，ti=(ti1,ti2,…,tim)T∈Rm，目标函数定义如下：

式中：g(x)为激活函数；Wi为输入层与隐含层之间的权重矩阵，Wi=(wi1,wi2,…,win)T；βi为隐含层与输出层之间的输出权重矩阵，βi=(βi1,βi2,…,βim)T；bi为第i个隐含层神经元的偏置；oj为第j个样本的网络输出值；C为隐含层神经元个数。

预测值与真实值误差最小，可表示为

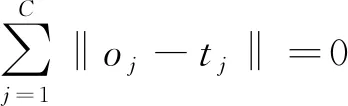
(8)

也就是存在βi、bi、Wi使得：

用矩阵表示为

Hβ=T

(10)

其中H(W1,…,WC,b1,…,bC,X1,…,XC)=

式中：H为隐层节点的输出；β为输出权重；T为期望输出。

1.3.2结合K折交叉验证与改进粒子群的ELM参数优化方法

粒子群 (particle swarm optimization, PSO)算法具有算法简单、收敛速度快、可调参数少、寻优能力强等优势，但是还存在一些不足[22]：随机产生初始位置，导致部分粒子位置距离最优解较远，影响了计算效率；参数设定较大时容易错过最优解，导致算法不收敛，或者其他粒子可能错过最优解，进而影响收敛速度和精度；可能出现“早熟”现象，导致局部极值点的出现。为避免出现上述情形，本文首先对PSO算法进行参数改进和变异操作，再以此为基础，提出结合K折交叉验证(K-fold cross validation, K-CV)与IPSO的ELM参数优化方法。具体步骤主要包括参数初始化、IPSO适应度函数选取、个体极值与群体极值的迭代更新和ELM最优参数生成。具体如下：

步骤1：初始化。给定训练样本[xi,yi] (xi∈RnIP，nIP为输入神经元个数，i=1,2,…,NIP，NIP为训练样本个数)，确定激励函数，并设置隐含层节点数C。初始化Np,IP个维数为D的参数向量tr,g(r=1,2,…,Np,IP)，其中任意一维的取值范围为[-1,1]，g表示迭代次数，D=C(nIP+1)。

粒子群种群个体t由极限学习机的输入权值向量a=(a1,a2,…,ac)和隐含层偏置矩阵d组成，t=(a11,a12,…,a1nIP,a21,a22,…,a2nIP,…,ac1,ac2,…,acnIP,d1,d2,…,dc)。对于每个种群个体tr,g，计算隐含层输出矩阵H，并计算输出权重β。

步骤2：适应度函数选取。计算10-CV的均方根误差作为IPSO的适应度，寻找平均均方根误差最小的个体。

步骤3：迭代更新。更新位置xi和速度vj，同时引入变异算子，在粒子更新之前有一定的概率初始化粒子速度和位置，计算适应度值，更新粒子的个体极值和群体极值。

步骤4：获得ELM最优参数。判断是否达到终止条件(达到适应度值预设精度或满足最小误差值或最大迭代次数)，则停止迭代，获得ELM最优参数组合；否则，回到步骤3。

1.4 评价指标

本文选用水文预报领域常用的评价指标，包括平均绝对百分比误差Emape、均方根误差Ermse、确定性系数Edc、相对误差Ere和合格率Eqr5种，以此综合评价预测模型的性能。各项评价指标的计算公式如下：

(11)

(12)

(13)

(14)

(15)

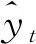
根据GBT 22482—2008《水文情报预报规范》，中长期径流预报的相对误差小于20%为合格。

2 实例验证

2.1 研究区域与数据资料

雅砻江流域位于青藏高原东部，地理位置界于96°52′～102°48′E、26°32′～33°58′N之间，北以巴颜喀拉山与黄河分水，东以大雪山与大渡河分界，西以雀儿山、沙鲁里山与金沙江上段相邻，南接滇东北高原的金沙江谷地。流域东、北、西三面大部分为海拔4 000 m以上的高山包围，其主峰均在5 500 m以上，南面分水岭高程较低，约2 000 m左右[23]。雅砻江流域及其站点分布如图1所示。用于雅砻江流域中长期径流预测的相关资料包括：①1951年1月—2011年12月，130项大气环流因子数据(本文选取与雅砻江流域相关的21项遥相关气候因子)；②1960年1月—2012年9月的气压、温度、湿度、降水、风速、日照等气象资料；③1960年1月—2016年12月的两河口、锦屏、官地、二滩水文站径流资料；④1998年4月—2008年7月的归一化植被指数(normalized difference vegetation index, NDVI)数据(旬尺度)。

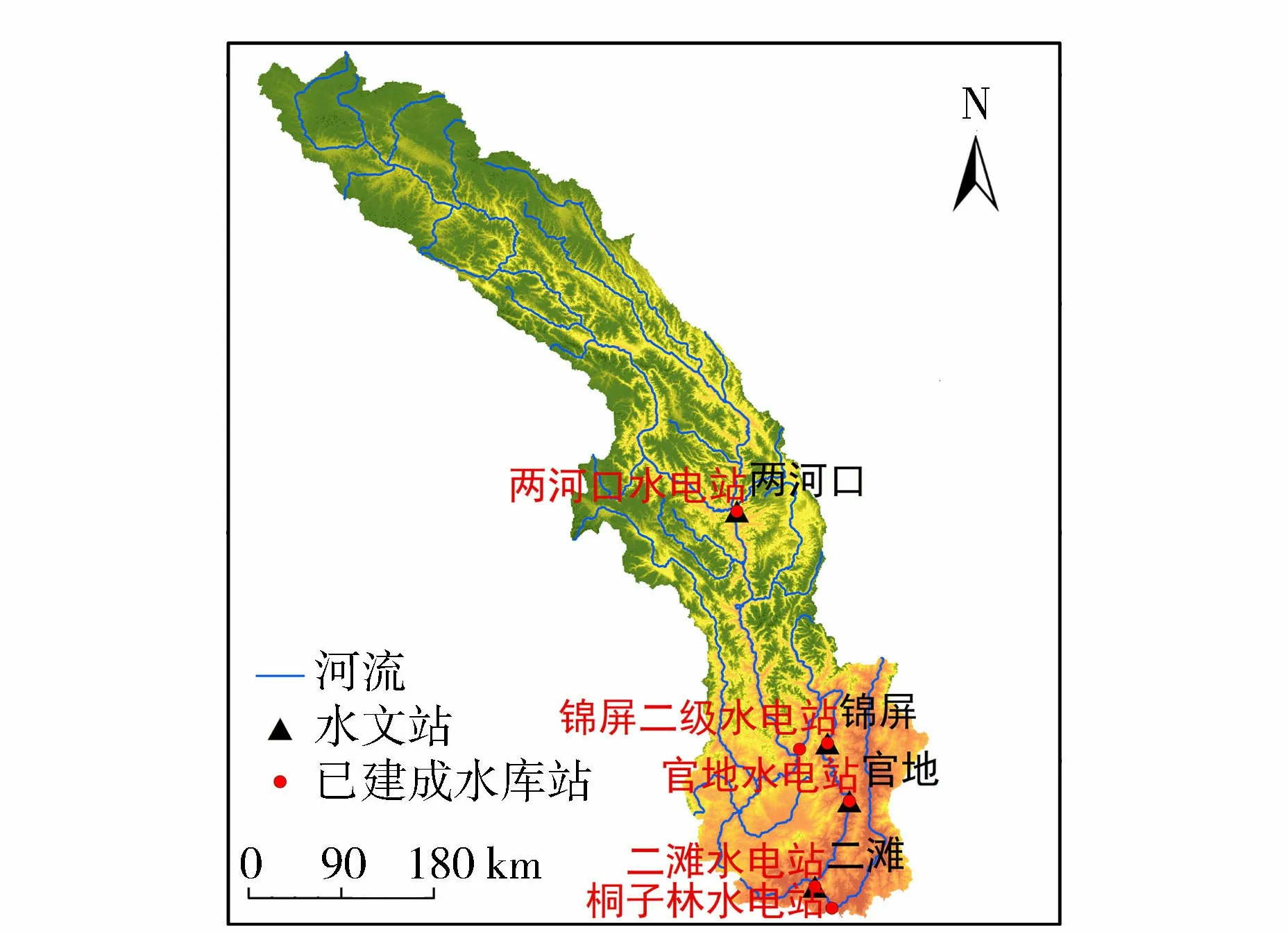
图1 雅砻江流域及其站点分布

考虑水文时间序列的一致性，以及比较不同水文要素对流域径流的影响，本文将数据集分为D1和D2两组。其中，D1数据集时间跨度为1998年4月—2008年7月，包括前期流域径流综合指数、面雨量指数、遥相关气候因子共计124组样本；D2数据集时间跨度为1998年4月—2008年7月，包括前期流域径流综合指数、面雨量指数、遥相关气候因子，以及植被指数数据共计124组样本。

2.2 径流综合指数构造结果

本文首先对雅砻江流域4个水文站(两河口、锦屏、官地、二滩)进行月平均径流一致性分析，结果表明上述站点之间保持着很高的相关性(图2)，因此基于上述水文站点的月平均径流(细粒度)，构造流域径流综合指数(粗粒度)；然后根据式(1)(2)，计算不同水文站点权重，结果如表1所示；最后构建径流综合指数，并与4个水文站的月平均径流进行Pearson相关性分析，结果表明构建的径流综合指数与4个水文站的月平均径流高度相关(表2)。

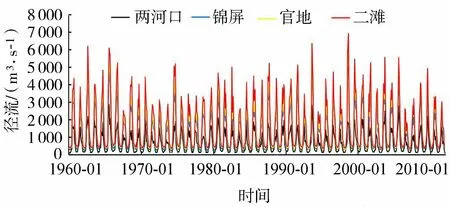
图2 流域内4个水文站月平均径流一致性对比

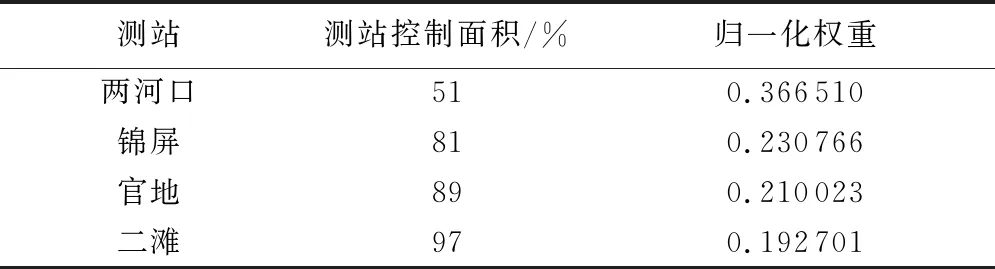
表1 基于4个水文站点流域控制面积构建流域径流综合指数权重

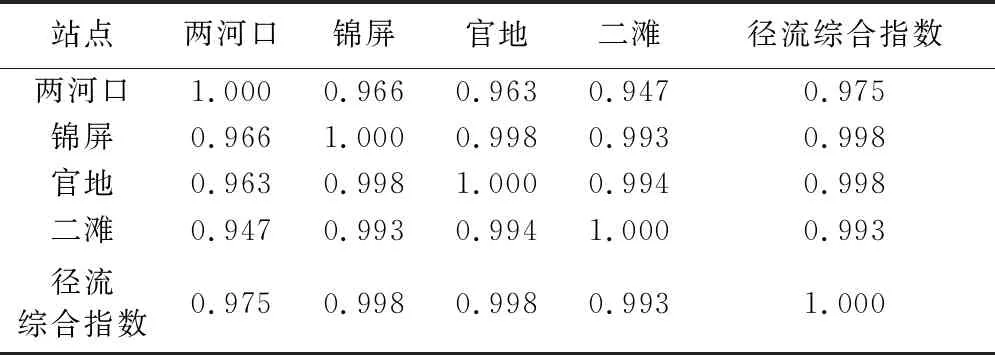
表2 径流综合指数与4个水文站月平均径流量Pearson相关性分析

2.3 基于偏互信息法的因子筛选结果

D1数据集的候选因子包括雅砻江流域径流综合指数因子fcom(fcom(t-1)，fcom(t-2), …,fcom(t-12))、面雨量指数因子frain(frain(t-1)，frain(t-2)，…,frain(t-12))，21个遥相关气候因子fatm1(fatm1(t-1)，fatm1(t-2)，…,fatm1(t-12))，fatm2(fatm2(t-1)，fatm2(t-2)，…,fatm2(t-12))，…,fatm21(fatm21(t-1),fatm21(t-2)，…,fatm21(t-12))等23个对象前期12个月的观测值作为备选特征，总数为276(23×12)个；D2的候选因子则包括雅砻江流域径流综合指数因子、面雨量指数因子、21个遥感相关气候因子，以及植被指数因子fndvi(fndvi(t-1)，fndvi(t-2)，…,fndvi(t-12))等24个对象前期12个月的观测值作为备选特征，总数为288(24×12)个。具体如表3所示。

表3 雅砻江流域中长期径流过程变化影响候选因子

为研究不同水文要素对中长期径流预测效果的影响，并考虑自回归项对整个因子筛选的影响太过显著等特点，基于赤池信息准则方法并不完全适用于雅砻江流域径流变化过程的因子筛选。因此，本文将在PMI方法基础上结合人工挑选方式进行因子选择：采用PMI方法对所有备选因子按照相关性大小进行排序，并在此基础上分别选择各自相关性大小排名前20的备选因子；以此为基础，再通过人工挑选方式分别在D1与D2数据集上选取上述几类水文对象中相关性大小各自排序前列的因子(最多排名前五)，最终组合形成新的综合筛选结果。其中，D1数据集筛选后的因子为11个，D2为13个，具体如表4所示。

表4 不同数据集的因子筛选结果

2.4 基于IPSO-ELM模型的流域中长期径流预测

2.4.1数据集划分

本文将D1与D2数据集划分为两部分，一部分数据用于预测模型的10折交叉验证(10-CV)，称为交叉验证期；另一部分数据用于模型测试。其中，用于10-CV的数据为1998年4月—2006年7月共计100组样本(随机选取90组用于训练，余下10组用于验证模型)，测试数据为2006年8月—2008年7月共24组样本。交叉验证期与测试期数据划分如表5所示。

表5 交叉验证期及测试期数据划分

2.4.2参数设置

粒子群算法初始化为：种群规模为40，最大迭代次数为400，粒子位置区间为[-2,2]，粒子速度区间[-0.5,0.5]，其他参数设置为c10取值2.2，c11取值1.2，c20取值0.3，c21取值2.2，p0取值0.01，p1取值0.28，w0取值1，w1取值0.1，学习速率为0.1，训练目标为0.001。适应度函数选择ELM的10折交叉验证的平均均方根误差，ELM的激活函数选择“sigmoid”。

为了保证对比试验的可靠性，本文对BPNN和SVM算法进行了相应优化，其初始参数设置分别为：BPNN基于10-CV方法，采用与ELM相同的结构，训练函数选择“tansig”，学习函数选择“logsig”，最大训练次数为600，学习速率为0.1，训练采用LM算法，动量因子为0.9，期望误差为0.001；支持向量机回归模型选择径向基核函数，采用10-CV方法，通过多次试验寻找最佳参数：径向基核函数中的σ=0.5，惩罚参数Ca=1，ε=0.001。

2.4.3训练结果及分析

在10-CV阶段，5种预测模型在D1与D2数据集上均具有较好的训练效果，其中IPSO-ELM模型在Emape、Ermse和Edc3个指标方面整体优于其他4种预测模型，显示了本文所提算法在该阶段具有较好的拟合效果和泛化能力。另外，5种预测模型在D1数据集上的交叉验证效果整体优于D2，说明当样本较少时，考虑参与的径流影响要素越多，效果反而较差。不同预测模型在D1与D2数据集上的10-CV性能对比如表6所示。

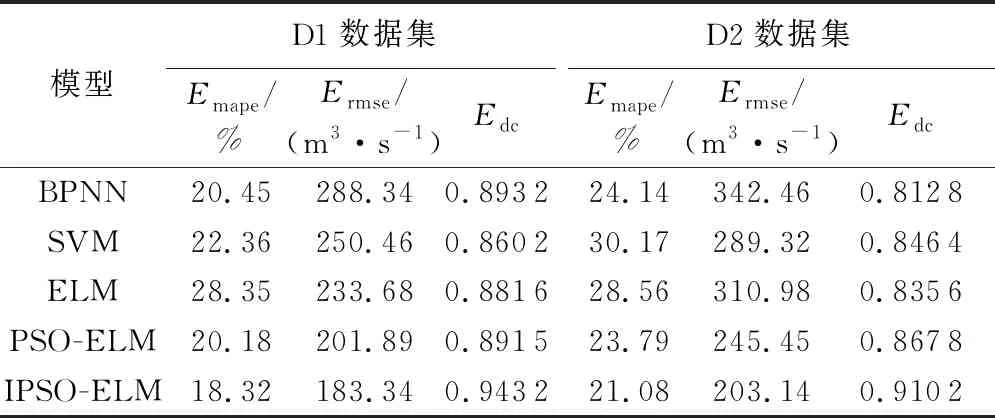
表6 不同模型在D1与D2数据集上10-CV的性能比较

2.4.4预测结果及分析

考虑到模型评测结果的可靠性，在D1与D2数据集上，测试集设计为2006年8月至2008年7月共24组样本数据，对比模型选用BPNN、SVM、ELM和PSO-ELM。IPSO-ELM模型分别与其他4种模型在D1与D2数据集上的预测结果对比如图3所示。相对误差对比曲线如图4所示，综合性能对比如表7所示。

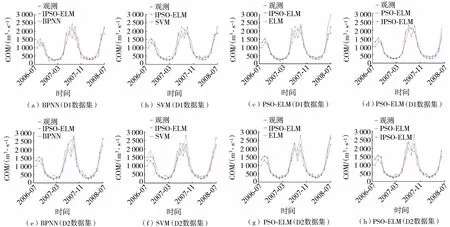
图3 IPSO-ELM模型与其他4种模型在D1与D2数据集上的预测结果对比

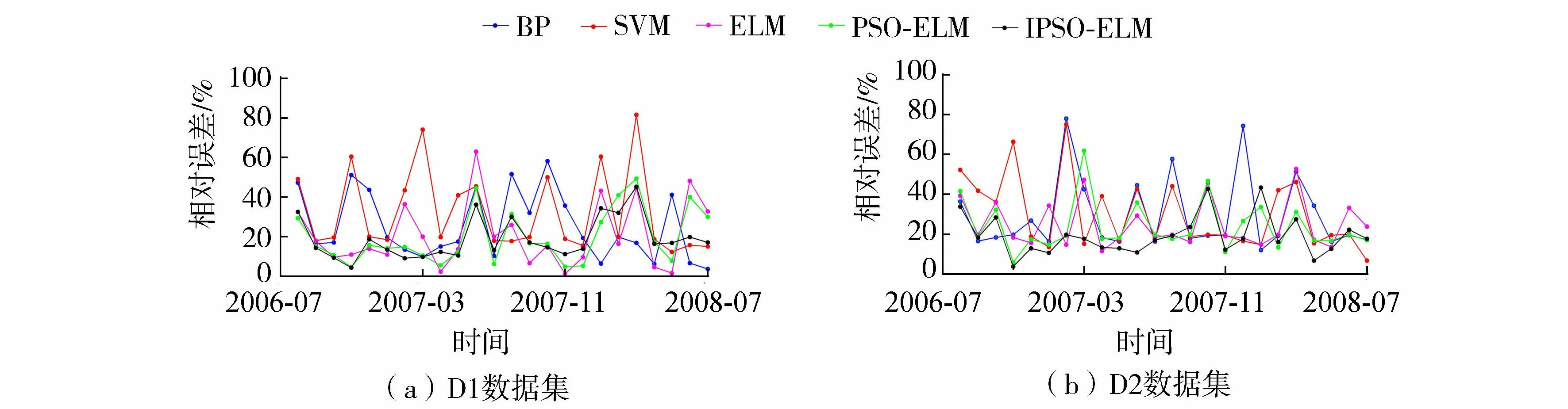
图4 不同模型在D1与D2数据集上的相对误差对比曲线

表7 不同模型在D1与D2数据集上的综合性能对比

2.4.4.1 不同模型预测结果比较

在D1数据集上，5种预测模型均具有较好的预测效果，但在不同的评测指标上展现出具有差异性的结果。其中：在Emape指标上，IPSO-ELM模型最优，相比较，SVM在该项指标上得分较低；Ermse指标与研究区域的年来水量紧密相关，年来水量大的流域，其Ermse指标也较大，其中IPSO-ELM模型的Ermse最小，相比较，BPNN模型较大；在Edc指标上，5种预测模型的确定系数都较高，其中IPSO-ELM模型最优，说明5种预测模型在基于信息熵的因子筛选基础上对流域中长期径流预测都具有较好的拟合效果；在Eqr指标上，5种预测模型的合格率都较高，其中IPSO-ELM模型最优(IPSO-ELM为75%，BPNN为62.5%，SVM为58.3%，ELM为66.7%，PSO-ELM为66.7%)，说明5种预测模型均可以应用于水文作业，其中基于IPSO-ELM模型的预报方案属于乙等，可用于向水文部门正式提供预报成果。

在D2数据集上，5种预测模型均具有较好的预测效果，但在不同的评测指标上展现出具有差异性的结果。其中：在Emape指标上，IPSO-ELM模型最优，相比较，BPNN和SVM在该项指标上得分较低；在Ermse指标上，IPSO-ELM模型最优，相比较，BPNN和SVM的均方根误差较大；在Edc指标上，IPSO-ELM模型较好，相比较，BP和SVM的确定性系数较低；在Eqr指标上，5种模型的合格率都较高，其中IPSO-ELM模型最优(IPSO-ELM合格率为70.8%，BPNN为62.5%，SVM为58.3%，ELM为62.5%，PSO-ELM为66.7%)。

综上所述，5种预测模型在D1与D2数据集上均具有较好的预测效果。其中，IPSO-ELM模型的预测效果最佳。主要原因在于：BPNN和SVM模型结构相对复杂，参数在训练过程中需要初始化与不断优化调整，整体效率不高，而ELM具有参数设置简单、计算速度快、误差小、泛化能力强等优点，因而整体预测效果优于上述两种常用模型；针对传统ELM模型输入权值和隐含层阈值随机给定，可能导致部分隐含层节点失效问题，本文结合K折交叉验证与IPSO算法，加快了ELM模型参数寻优速度，因而提高了预测效果。

2.4.4.2 不同数据集上的预测效果比较

在增加径流影响要素的情况下，5种预测模型在D1数据集上的预测效果整体上胜于D2(增加了NDVI植被指数)，主要原因在于：流域径流影响要素增多导致模型的输入变量增加，从而增加了模型的计算复杂度，导致在D2数据集上的整体运算效率不如D1；与中长期径流预测有关的时间序列较短(训练样本较少)，模型难以充分学习，导致D2整体预测效果差于D1。因此，在流域径流影响要素增多时，模型的输入维度也相应增加，而时间序列又相对较短(训练样本较少)时，预测模型难以充分训练学习，整体预测效果可能会相对较差。