泵站进水池翼型导流板整流特性数值模拟
2021-09-14雷帅浩
罗 灿,雷帅浩,陈 锋,刘 浩,成 立
(1.扬州大学水利科学与工程学院,江苏 扬州 225009; 2.西华大学流体及动力机械教育部重点实验室,四川 成都 610039;3.常州市城市防洪工程管理处,江苏 常州 213000; 4.镇江新区水利站,江苏 镇江 212000)
截至2019年底,全国已建成中小型泵站占流量1 m3/s以上或装机功率50 kW及以上泵站的比例超过99%[1]。对于中小型泵站而言,其进水绝大多数采用的是进水池。泵站有正向进水和侧向两种进水方式。受工程布置条件限制时,往往采用侧向进水,进水条件欠佳,进水池常伴有旋涡、回流等不良流态[2],需要采取适当的整流措施。常见的整流措施有:①导流板[3]、导流墩[4-6]、导流栅[7-8]等导流措施,该种措施可以平顺地引导水流转向,明显改善池内水流流速分布,消除大尺度的回旋区,提高水流均匀性;②底坎[6,9-11]和立柱[12-14],其中底坎常用于前池整流,立柱的设置可以有效地破坏进水旋涡,使得水流重新分配;③压水板[15],该措施常设置在运行水位附近,通过约束面层水流,迫使面流和底流掺混,流速得以重新分布,进而改善池内流态,同时还能起到一定的消除池内淤积的作用。本文在前人的基础上,借鉴压水板挤压水流的原理,提出了一种翼型导流板,该翼型导流板利用挑流原理,使水流流速重新分布,进而改善水流流态。该研究一方面有助于拓宽整流思路,另一方面也可被同类泵站借鉴和采纳。
1 计算域及数值模拟方法
由于工程实际,某泵站将船闸和泵站合建,船闸航道同时作为泵站前池。为保证泵站正常运行,上闸首处于常开状态,航道即为泵站的前池,该泵站为典型的闸站式侧向进水泵站。为改善池内不良流态,考虑到前池作为航道,必须保证船舶通航条件通畅,不合适布置整流措施,故将整流措施设置于进水池内。图1为该泵站原型计算域示意图,包括前池、进水池和吸水管。该站共有4台轴流式水泵机组,单机流量1.5 m3/s,设计流量6 m3/s,设计进水管直径D=1 m,水深4D,进水池长9.5D,宽3D,喇叭管进口直径1.4D,悬空高与后壁距均为D。此外,两侧机组各有1个空置进水池作为扩容备用。
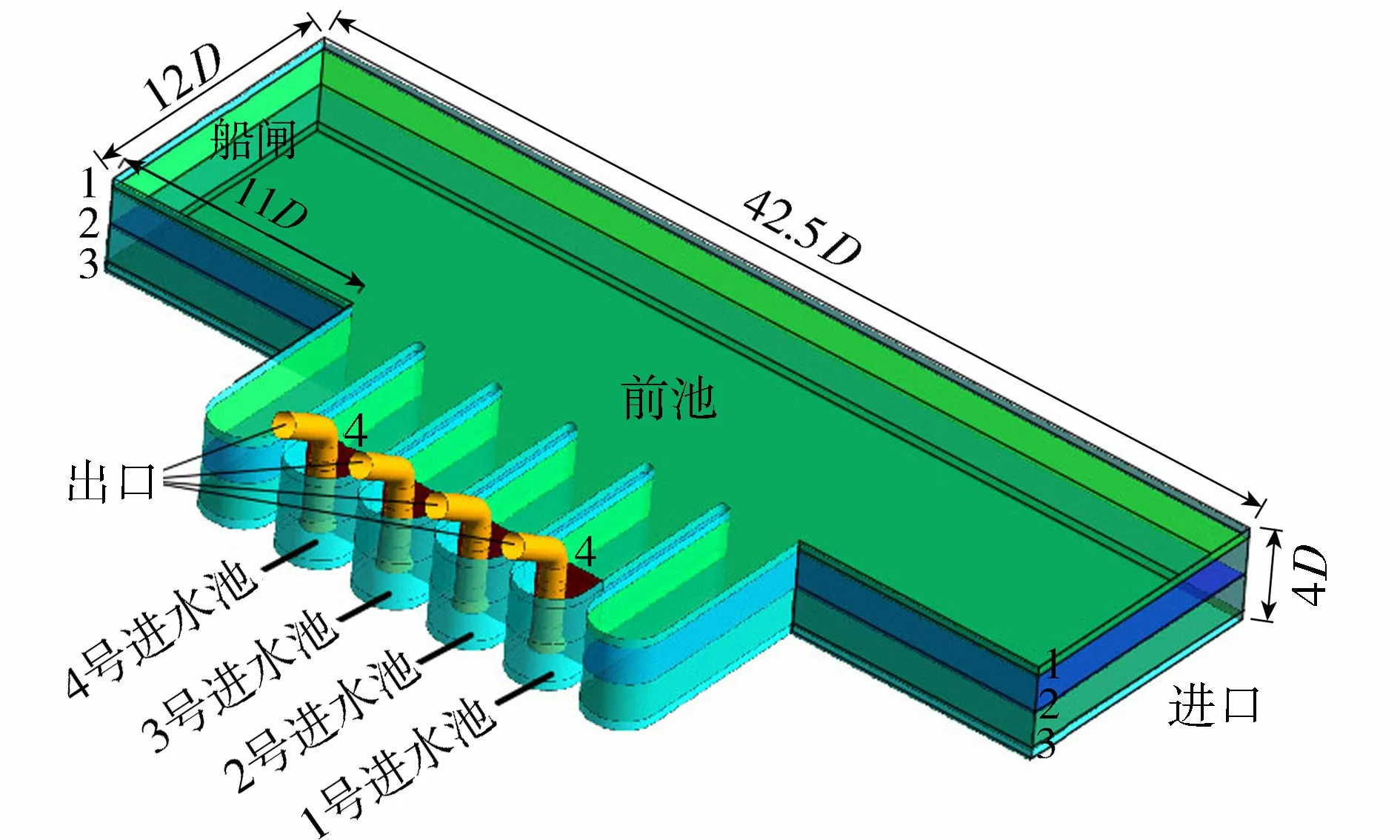
图1 计算域示意图
采用适应性强的非结构化网格对计算域进行了整体网格离散。为了避免网格可能对计算结果造成干扰,开展了网格无关性分析,选取进出口的水力损失作为特征参数,计算相邻网格方案的相对误差,结果表明:当网格数量超过183.1万时,水力损失误差在±2%以内,该网格数量满足计算要求。
通过计算该流动中的雷诺数,同时不考虑水的可压缩性,判定该泵站池内的流动为复杂的不可压缩紊流流动。基于RANS方程,采用Realizablek-ε湍流模型和SIMPLEC算法进行求解[10],获取计算域全流场数据。进口取前池入口处,流量为6 m3/s。出口取吸水管出口侧,设置为自由出流,参考压力为0.1 MPa。壁面设置为wall,采取scalable壁面函数对壁面处理。液面为自由水面,设为对称边界条件。
2 研究方案
2.1 特征断面选取
如图1所示,选取4个断面研究各方案进水池的流态。断面1—1距自由水面的距离为0.4D,用来分析进水池上层流态;断面2—2距自由水面的距离为2D,用来分析进水池中层流态;断面3—3距进水池底板的距离为0.4D,用来分析进水池下层流态;断面4—4距进水池后壁的距离为2.5D,用来分析吸水管前的流态。
2.2 方案设计
针对原方案(即无整流措施)进水池内存在的回流等不良流态,本文提出在进水池进口附近设置翼型导流板进行整流,翼型选用标准的NACA0012翼型,其弦长Lc=1D,最大厚度W=0.18D,如图2所示,图中翼型导流板参数分为几何结构参数和位置参数两类,几何结构参数有Lc、W和仰角α,位置参数有进口距L和距深比d′,其中进口距L指翼型导流板前缘距进水池进口的距离,距深比d′指翼型导流板的间距d和池内水深H的比值(当选用1个翼型导流板时,距深比d′指翼型导流板距池底的距离和池内水深的比值)。

图2 进水池内导流板布置
为了研究翼型导流板的几何结构参数和位置参数对进水池流态的影响,设计了等水平正交试验,其中试验因素有进口距A、仰角B和距深比C(表1),各因素水平为4。方案设计详见表2,其中翼型导流板L16(45)正交方案设计为表2中的方案1~16。
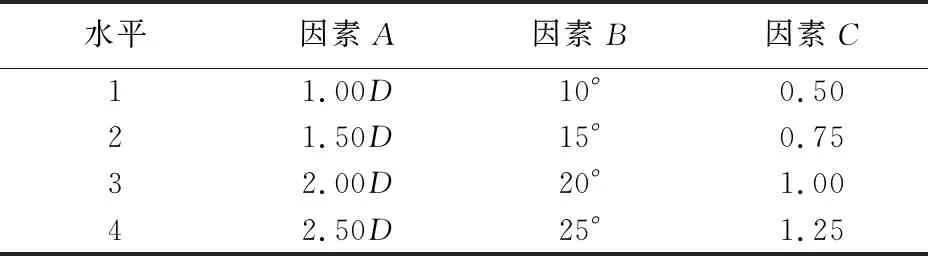
表1 翼型导流板因素及水平
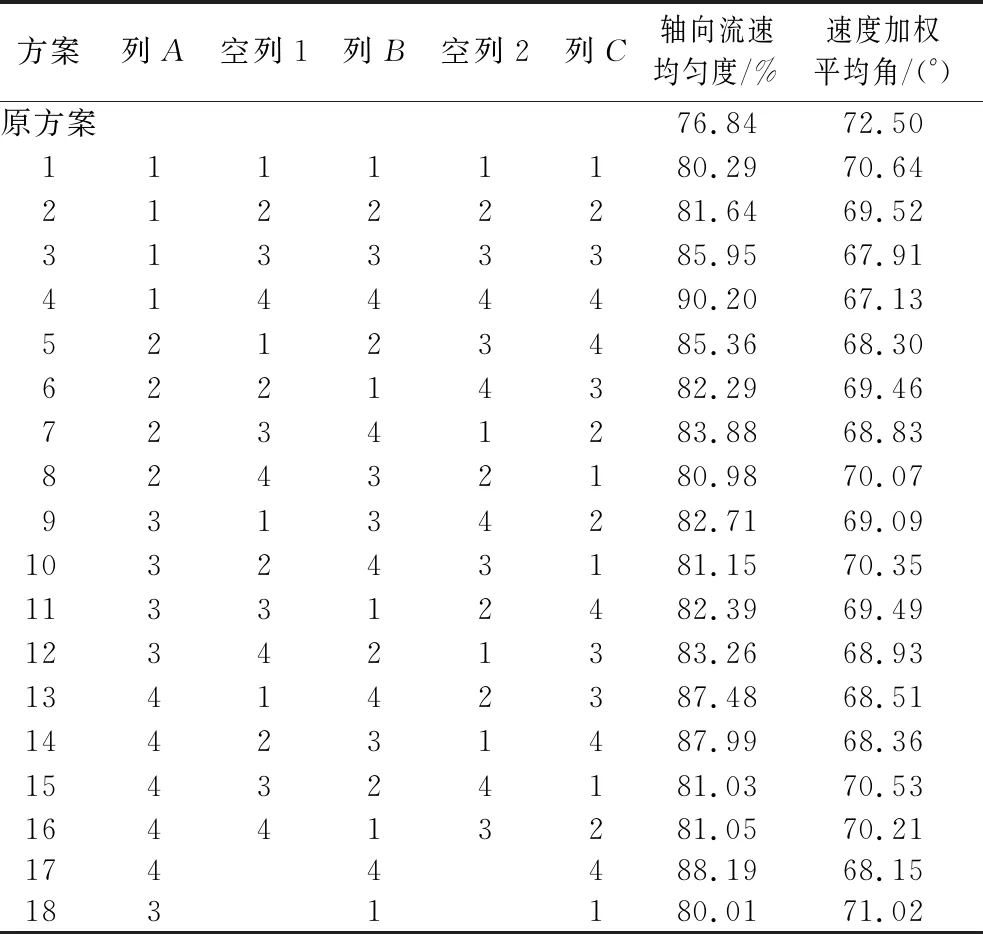
表2 方案设计及试验结果
注:考虑各方案下各进水池轴向流速均匀度和速度加权平均角不尽相同,为了综合分析各方案的整流效果,特选取每种方案下4个进水池特征断面4—4轴向流速均匀度和速度加权平均角的平均值作为流态评价指标。
3 整流效果分析
3.1 流态评价指标
一般而言,需要从流线分布和特征流动参数两方面进行流态的定性和定量分析。本文采用轴向速度分布均匀度Vau和轴向速度加权平均角θ对流态进行定量分析。轴向速度分布均匀度Vau用于评价特征断面上轴向流速的分布均匀程度,其数值越接近100%,断面流速分布越均匀;速度加权平均角θ则是断面轴向速度与断面的夹角,其数值越接近90°,流动平顺性越好[16]。其中,轴向速度分布均匀度的计算为
式中:vai为断面各节点轴向速度;va为断面平均轴向速度;n为节点数。
3.2 正交试验分析
计算各方案进水池纵剖面的轴向流速分布均匀度和速度加权平均角,将其列于表2中。采用直观分析法,对正交方案计算结果进行分析,得到试验因素的主次顺序及优化方案,计算结果分析见表3和表4。表中Ki为第i行对应的计算结果之和;ki为第i行所得计算结果的算数平均值;R为极差。

表3 轴向流速分布均匀度正交试验分析 %

表4 速度加权平均角正交试验分析 (°)
从表3和表4可以看出,各列的极差完全不同,说明各因素的水平对指标的影响不一,极差越大,说明该因素对指标的影响作用越大,其对应因素即为主要因素。无论是轴向流速分布均匀度还是速度加权平均角,C因素均为最主要的因素,其次为B因素,最后为A因素,即翼型导流板距深比对流态影响最大,其次为仰角,进口距对流态影响较小。此外,空列极差均小于3个因素的极差,这说明3个因素之间不存在不可忽略的交互作用。对于不同的指标,优化方案的选择完全不同,将轴向速度分布均匀度作为对比指标,因素主次排序为C、B、A,优化方案为方案4(进口距1D,仰角25°,距深比1.25),其次为方案17(进口距2.5D,仰角25°,距深比1.25),而将速度加权平均角作为对比指标,因素主次排序依然为C、B、A,优化方案为方案18(进口距2D,仰角10°,距深比0.5)。
图3为各指标趋势图,从中更直观地发现:对于两种流态评价指标,进口距2D均是其趋势线的拐点,当进口距小于2D时,轴向速度分布均匀度有随进口距增加而减小的趋势,速度加权平均角则随进口距增加而增加;轴向速度分布均匀度随仰角和个数增加而增加,速度加权平均角变化趋势完全相反;当进口距为1D,仰角为25°,距深比为1.25时轴向速度分布均匀度最大,其次是进口距为2.5D,仰角为25°,距深比为1.25时;当进口距为2D,仰角为10°,距深比为0.5时速度加权平均角最大。

图3 各指标趋势
选取具有代表性的方案4、5、12、17与原方案进行对比,分析进水池三维涡带分布图,进而定性分析各指标趋势线的拐点现象,如图4所示。
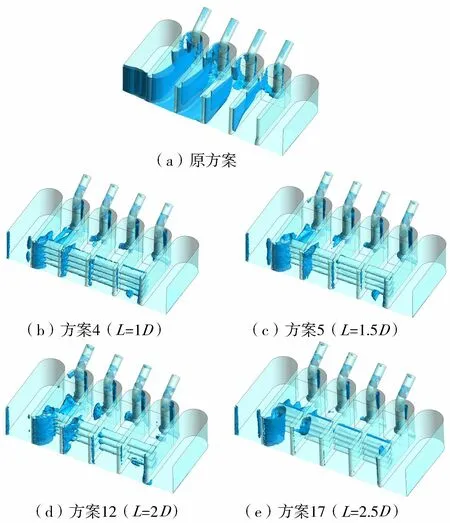
图4 进水池涡分布
从图4(a)不难看出:原方案下,1号进水池存在大尺度的涡,从进口持续到吸水管,从底层持续到面层,其中,立面涡约占该进水池一半的区域,断面4—4近一半多的区域被立面涡包围;2号进水池涡相比1号进水池范围缩小一半,从进口持续到吸水管,从底层持续到面层,断面4—4约30%的区域被立面涡包围;3号进水池立面涡尺寸明显减小,仅在进口和吸水管进水侧存在,断面4—4较小范围被立面涡包围;4号进水池立面涡大大缩小,仅存在于进水池进水侧上层,断面4—4很小范围被立面涡包围。从图4(b)~(e)明显发现:①对于1号进水池,翼型导流板前立面涡尺度与其进口距成正比关系,立面涡经过翼型导流板后变为附底涡,附底涡持续到吸水管附近,在进口距L=2D之前,附底涡尺度随进口距的增加单调递增,但当进口距超过2D后,其变化趋势刚好相反,与图3进口距对进水池流态指标影响趋势一致;当进口距L=1D时,翼型导流板从涡的前端完全破坏了此涡,水流经翼型导流板重新分布流速后,进水池底部存在充分发展的小尺度附底涡,断面4—4附近附底涡尺度最小;当进口距L=1.5D时,翼型导流板从涡的前中部破坏了该涡,一般充分发展的附底涡尺度与方案4相比有所增大,尤其在断面4—4附近最为明显;当进口距L=2D时,翼型导流板从涡的中部破坏了该涡,较充分发展的附底涡尺度与方案5相比明显增大,其中断面4—4附近附底涡变大趋势最为明显;当进口距L=2.5D时,翼型导流板从涡的后部开始破坏,重新分布的流速距吸水管过近,由于喇叭口的吸束作用,附底涡未得到充分发展就进入吸水管,部分发展的附底涡尺度较方案4大、方案5和方案12小,尤其在断面4—4附近最为明显。②对于2号进水池,翼型导流板前立面涡尺度与1号进水池变化趋势一致,经过翼型导流板后仅在翼型导流板下表面、后缘以及后壁处存在小的涡团;③对于3号和4号进水池,进水池内立面涡均消失,翼型导流板附近和后壁处存在小的涡团。故图3出现了拐点现象。
3.3 断面流态分析
从表3和图3中不难发现,不同指标对应的优化方案完全不同,为了进一步确定进水池整流的最佳措施,并对正交试验进行验证,这时考虑各优化方案及原方案下进水池的横断面流态。
图5为进水池面层流态,可以发现:原方案下,1号进水池近一半的区域存在大尺度的旋涡(图中红色线框),主流严重偏向进水池右侧,2号进水池左侧进口附近有回旋区,主流整体偏右,后壁存在绕流,3号进水池进口左侧有回旋区,后壁有小范围的旋涡,4号进水池流线分布均匀对称,后壁有较大范围的旋涡;方案4下,进水池回旋区消失,流线分布均匀,仅在进水管后面和1号进水池进口附近形成小范围旋涡,流态整体很好;方案17下,1号进水池回旋区减少90%左右,左侧进口附近存在有横向流速,2号和3号进水池左侧回旋区完全消失;方案18下,1号进水池流态得到改善,回旋区减少30%左右,2号进水池流态无明显变化,3号进水池左侧回旋区消失,3号和4号进水池后壁处有小范围旋涡。从进水池面层流态明显看出,方案4下的进水池流态最好,流线更均匀对称。
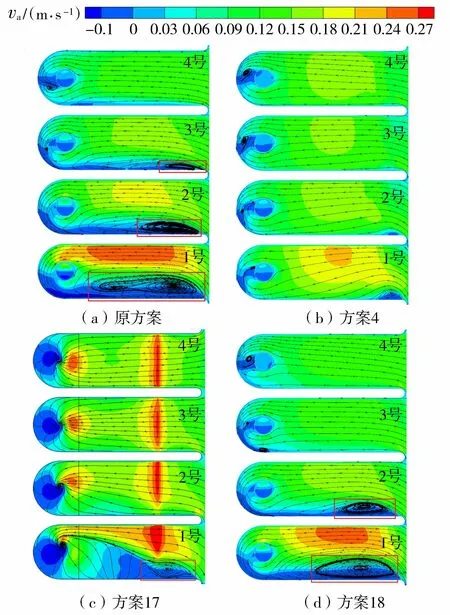
图5 进水池面层流态
图6为进水池中层流态,可以发现:原方案下,1号进水池被大面积的回旋区占据,回旋范围相比面层流态有所扩大,主流严重偏右,2号进水池左侧存在回旋区,回流从进口延伸至进水管前端,回旋范围相比面层流态略有扩大,主流整体偏右,后壁有绕流存在,3号进水池左侧有较小的回旋区,后壁存在绕流;方案4下,进水池大尺度回旋区完全消失,流线分布均匀对称,仅在进水池后壁处和1号进水池进口附近形成小范围旋涡,整体流态很好;方案17下,1号进水池回旋区减少90%左右,2号和3号进水池回旋区消失,与方案4相比,1号进水池旋涡范围明显更大;方案18下,1号进水池回旋区减少了60%左右,2号和3号进水池左侧回旋区消失,4号进水池后壁有小范围旋涡,1~3号进水池后壁存在绕流。从进水池中层流态明显看出,方案4下的进水池流态最好,流线分布更均匀对称。
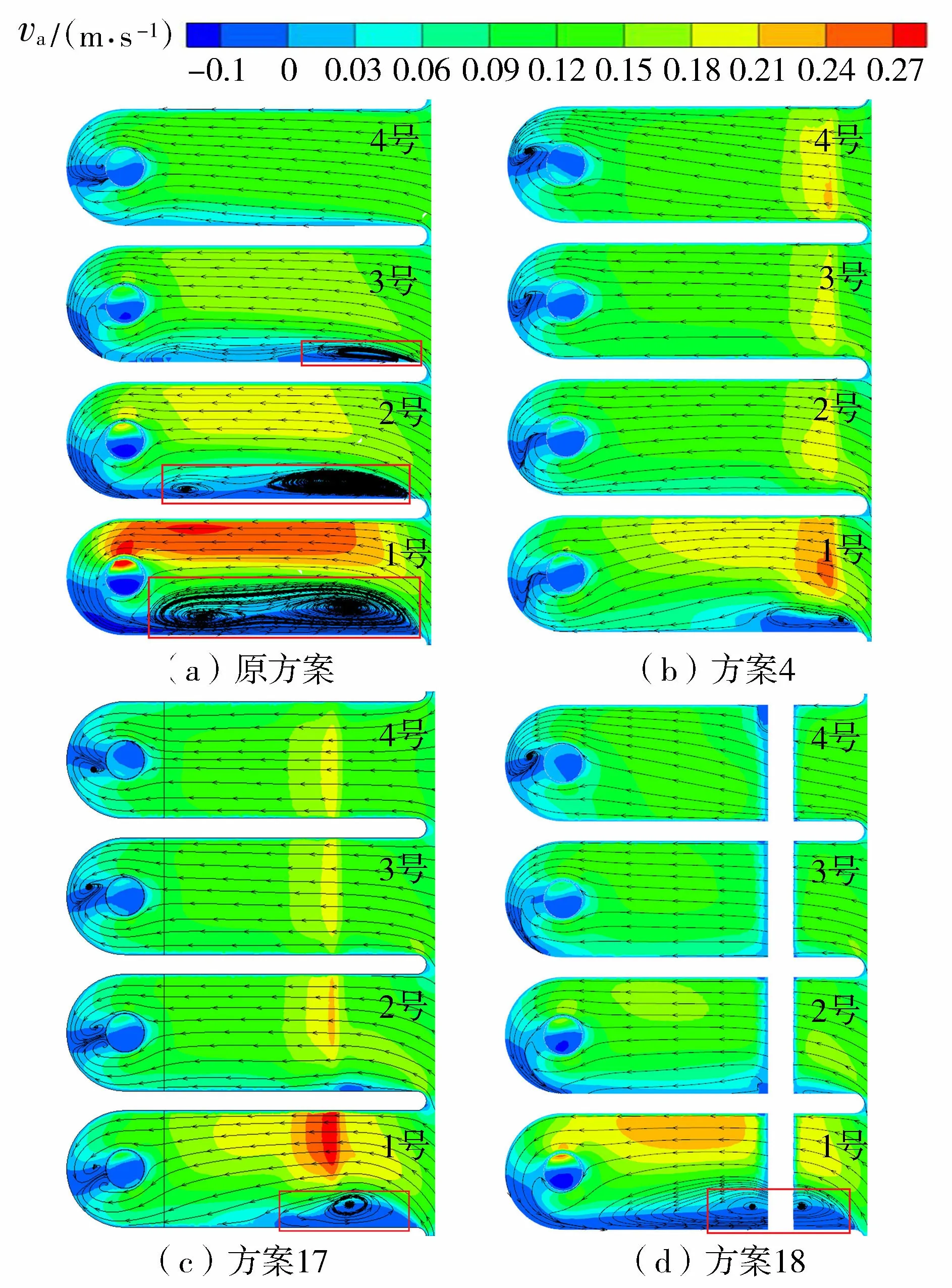
图6 进水池中层流态
图7为进水池底层流态,不难发现:原方案下,1号进水池存在大面积回流区,回流区相比面层和中层流态有所扩大,主流明显偏右,2号进水池左侧存在回旋区,回流区相比面层和中层流态变小,1~3号进水池后壁处流线从进水池右侧逆时针旋转流向进水管,流线分布不对称;方案4下,1号进水池负流速区域明显变小,左侧进口附近存在有横向流速,后壁处流线大部分对称流向进水管,2号进水池回旋区消失,后壁处流线基本对称流向进水管,3号进水池后壁处流线均匀对称流向进水管;方案17下,1号进水池回旋区减少60%左右,2号进水池回旋区减少50%左右,进水池后壁存在小的旋涡;方案18下,1号和2号进水池回旋区有所减少,后壁流线分布较原方案相对对称,3号进水池后壁流线分布明显均匀对称。从进水池底层流态明显看出,方案17下的进水池流态最好,流线分布更均匀对称。

图7 进水池底层流态
3.4 断面流速均匀分析
图8为进水池纵剖面轴向速度云图。原方案下1~4号进水池左侧均存在负流速区,流速分布严重不均,其中1号和2号进水池流态最差;方案4和方案17下各进水池负流速区消失,1号和2号进水池流速分布基本均匀,3号和4号进水池流速分布均匀对称;方案18下1号和2号进水池负流速区减少了一半之多,但流速分布依旧严重不均,3号和4号进水池负流速区消失,流速分布比较均匀对称。

图8 4个进水池纵剖面轴向速度云图
表5为进水池纵剖面流态评价指标表。原方案下,各进水池的轴向速度分布均匀度不高,平均为76.84%,纵断面速度加权平均角平均值为72.5°;方案4下,轴向速度分布均匀度极大,最大提高至91.36%,平均提高了13.36%,提高率为17.4%,而纵断面速度加权平均角有所下降,平均减少了5.37°,下降率为7.9%;方案17下,轴向速度分布均匀度明显提高,平均提高了11.35%,相比方案4少提高2.01%,而纵断面速度加权平均角有所下降,平均减少了4.35°,相比方案4少减少1.02°;方案18下,轴向速度分布均匀度有所提高,平均提高了3.17%,而纵断面速度加权平均角略有下降,平均减少了1.48°。综合考虑纵剖面速度云图及流态评价指标表,不难看出,方案4整流效果最为明显。

表5 4个进水池纵剖面流态评价指标
综合考虑断面流态和断面流速均匀性,明显看出方案4整流效果最为明显。为了进一步分析方案4的整流特性,特选取流态最差的1号进水池,截取其回流区涡核中心进行流态研究,该截面距进水管中心线0.8D,图9为进水池立面涡图(y=0处为进水池进口)。无整流措施下,1号进水池存在大尺度的立面涡(图中红色线框区域),旋涡中心距进水池进口5.3D,距池底0.6D,对进水管附近的流态影响较大。设置翼型导流板后,流态明显改善,立面涡范围明显缩小一半之多,旋涡强度中心向前移动2.2D,向上移动0.1D,旋涡明显提前,对进水管附近的流态影响较小。
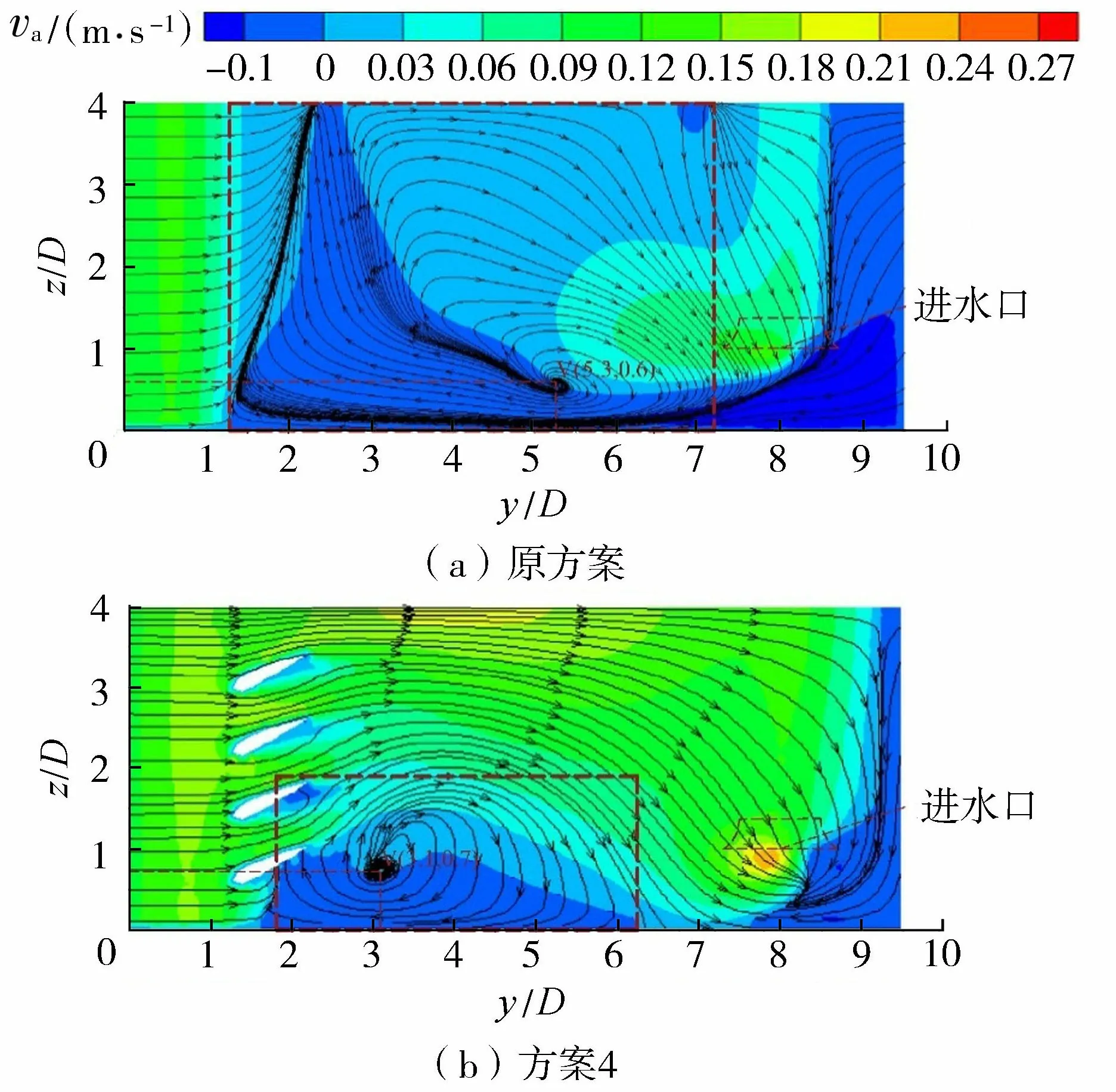
图9 进水池立面涡
4 结 论
a.原方案下,1~3号进水池均存在大尺度的回旋区,流态极其不好,流速分布不均匀,其中1号进水池回旋区占据半个进水池;
b.翼型导流板可以有效破坏进水池内涡,使得破坏后的水流沿其上表面和下表面流动,流速场得到最大程度的均匀分布;
c.方案4(进口距为1D,仰角为25°,距深比为1.25)下,进水池大尺度回旋完全消失,流速分布均匀,轴向流速分布均匀度大幅上升,最大提升至91.36%,速度加权平均角小幅下降,整流效果最佳。
