考虑损伤的混凝土非线性徐变模型

2021-09-14蔡昊男李鑫鑫

水利水电科技进展 2021年4期

郑丹，蔡昊男,李鑫鑫

(重庆交通大学河海学院,重庆 400074)

混凝土结构在长期持续荷载作用下变形不断增加的现象称为徐变[1]。在不同大小的长期荷载下，混凝土表现出不同的徐变现象。当长期荷载较小时(<0.4fc，fc为抗压强度)，混凝土变形随时间增加缓慢，且徐变变形与应力成正比，此时为线性徐变；当持荷水平较大时，徐变虽最终收敛但和应力水平不再成线性，此时为非线性徐变；在持续荷载很大时(>0.7fc)，混凝土徐变将不再收敛，此时混凝土将发生徐变破坏(Tertiary creep)[2]。由于高拱坝等水工结构在服役期承受较高水平的持续荷载，准确地计算混凝土非线性徐变对结构分析设计十分重要。

混凝土在较低荷载水平下的线性徐变计算发展已经非常成熟，如CEB-FIP模型[3]，ACI209模型[4]，朱伯芳模型[5]和Bazant的固化徐变模型[6]等，但目前对高持续荷载非线性徐变研究还比较欠缺。大量试验研究表明，较高持续荷载下的混凝土在徐变变形过程中材料会发生损伤[7-8]，混凝土在徐变过程的损伤是导致非线性徐变的主要原因[9]。在试验基础上，研究人员提出了各种模型分析混凝土的非线性徐变性能。Mazzotti等[10-11]采用广义的Kevin和Maxwell弹簧阻尼模型，黄耀英等[12]采用串联Bingham原件建立了宏观的混凝土非线性徐变模型。郑丹[13]假设单元应变能服从Weibull分布，采用统计损伤模型分析了持续荷载下混凝土的力学性能。陈忠等[14]应用最小二乘法回归分析徐变度的试验数据，并提出了基于时间等效的混凝土徐变模型。Ruiz等[15]认为混凝土在徐变过程中的损伤机理与在疲劳应力下相似，分析了混凝土的非线性徐变行为。Ren等[16]采用能量为基础的塑形损伤模型，建立混凝土的非线性徐变模型。Luzio[17]将细观层面的固化徐变模型引入微平面理论框架，分析了徐变与损伤的耦合关系。同时，美国垦务局[18]进行了持续时间超过10 a、荷载水平为1/4～1/3混凝土抗压强度的试验，结果表明低应力作用的徐变并不会对混凝土材料造成损伤。可以看出，目前的混凝土非线性徐变模型大多试验数据的直接拟合，或是直接认为部分徐变变形会导致混凝土损伤，并没有反映混凝土非线性徐变的机理。

1 非线性徐变系数

在现有理论和试验研究基础上，研究人员一般用非线性徐变系数F(η)来描述较高荷载下混凝土的徐变变形：

(1)

式中：σc为持续荷载；Ec为弹性模量；η=σc/fc为持荷应力水平；φlin(t0,t)为无量纲线性徐变，为非线性徐变系数。现有文献中非线性徐变系数计算公式如表1所示，其中非线性临界点表示线性和非线性徐变的分界点，即持续荷载水平超过该值后，混凝土发生非线性徐变。

表1 现有非线性徐变系数计算公式

可以看出，不同研究人员得出的非线性徐变系数计算方法形式差别较大，不同计算方法得到非线性徐变系数和持荷应力水平的关系如图1所示。图中还给出了文献中不同强度等级的非线性系数试验数值。

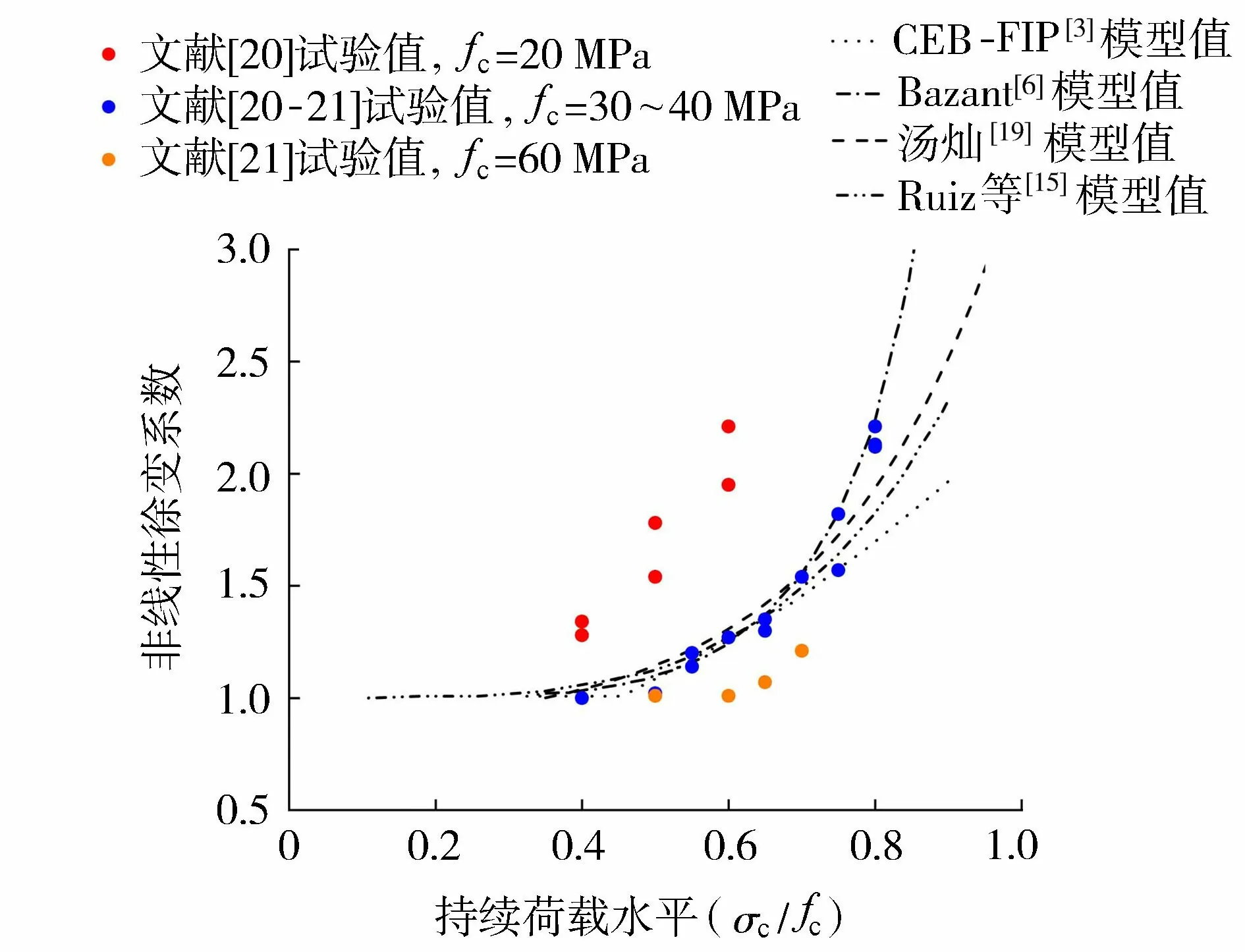
图1 非线性系数与持荷水平关系

从图1中可以发现，现有非线性徐变系数计算公式和中等强度混凝土(C30，C40)试验结果吻合较好，但不能反映较低(C20)和较高强度混凝土(C60)的非线性徐变特征。这是因为目前的非线性徐变计算方法均是试验数据的宏观拟合，没有考虑混凝土材料在持续荷载下的非线性变形力学本质。因此有必要分析较高持续荷载下混凝土徐变和损伤耦合机理，提出能准确计算不同强度等级混凝土非线性徐变变形的方法，为长期服役的混凝土结构安全性评价提供参考。

2 考虑损伤的混凝土非线性徐变计算方法

2.1 混凝土非线性徐变模型

根据已有的理论和试验研究成果，笔者认为混凝土在高持续荷载下体现出非线性徐变特征主要是由材料损伤造成的。在较高荷载下混凝土材料内部会发生损伤，损伤变形会减小材料的宏观弹性模量，虽应力不变但徐变变形增加；同时徐变变形会导致材料发生损伤，损伤与徐变相互耦合，导致高持续荷载下混凝土徐变呈现出非线性。考虑混凝土材料损伤，可以将高持续荷载下混凝土的应变划分为以下3个部分：

εtot=εe+εd+εc

(2)

式中：εtot为徐变总应变；εe为混凝土弹性应变(瞬时且可恢复)；εd为损伤应变(瞬时不可恢复)，主要与混凝土中的微裂纹扩展演化有关；εc为混凝土基体徐变应变，主要是由水泥基基体的流变特性产生的，与塑性收缩以及骨料、加载龄期等诸多因素相关。

式(2)中，混凝土弹性应变可以通过混凝土单轴抗压应力应变关系计算得出。对于混凝土基体徐变应变，本文采用Bazant[22]等提出的固化徐变B3模型计算，其增量形式的徐变度C0(t,t′)可表示为

g′(t)=C0(t,t′)=n(q2t-m+q3)/

[(t-t′)+(t-t′)1-n]+q4/t

(3)

q2=451.1c0.5(fc)-0.9q3=

0.29(w/c)0.4q2q4=0.14(a/c)-0.7

(4)

式中：t和t′分别为计算和持荷开始龄期；w/c为水灰比；a/c为骨料与水泥比值；n和m为常数；q2～q4分别为与龄期相关的黏弹性相柔度、与龄期无关的黏弹性相柔度和黏性相柔度。根据Lemaitre的损伤力学理论，将材料损伤D表示为弹性模量的折减，单轴情况下混凝土等脆性材料的本构关系可以表示为

(5)

式中：σ*为作用在材料上的有效应力；σ为外部应力；E′和E分别为材料损伤后的弹性模量和初始弹性模量。考虑材料损伤后，实际作用在材料的有效应力增加，徐变变形增大，因此增量形式的混凝土基体徐变可以表示为

(6)

从上述分析可以看出，对于弹性应变以及基体徐变应变可以通过现有的研究成果进行确定，但损伤应变εd无法直接计算。因此，准确计算混凝土非线性徐变变形的关键是确定损伤应变εd，即明确徐变变形如何对混凝土材料造成损伤。

2.2 混凝土徐变变形产生的损伤

混凝土的损伤破坏主要是由材料内部微裂缝、孔隙扩展演化造成的。根据Griffith经典断裂理论，在外荷载作用下，材料内部应变能逐渐累积，当应变能超过产生新裂纹需要的表面能时，裂缝就会发生扩展。

如图2所示的经典线弹性断裂模型，厚度为B的平板承受均匀拉应力σ，由于裂纹存在而释放的弹性能U(平面应力条件下)和裂纹扩展形成新表面所需表面能S分别为

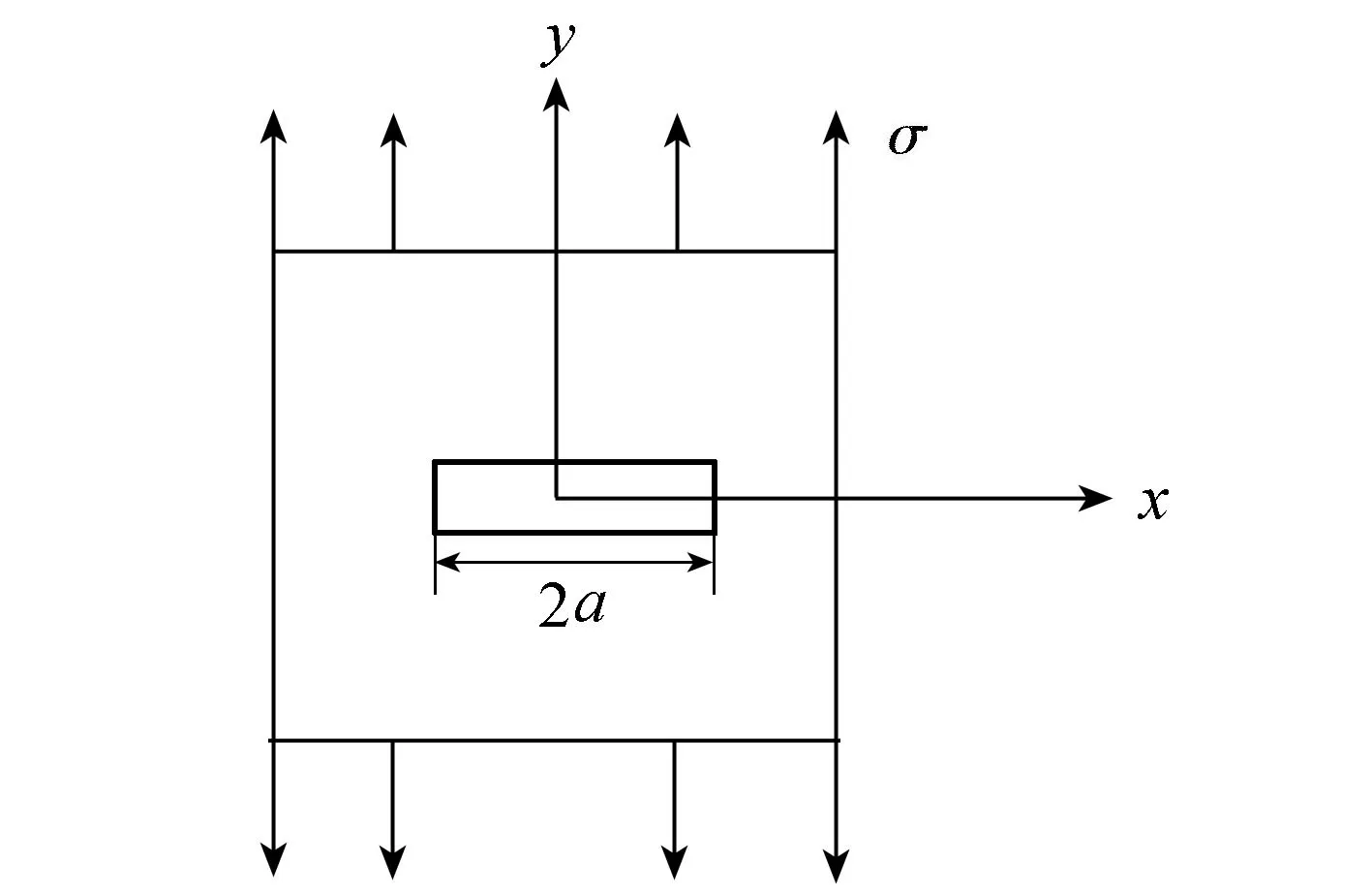
图2 拉伸应力下I型裂缝

U=πa2σεB=πa2σ2B/E

(7)

S=2Aγ=4aγB

(8)

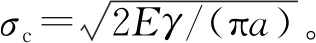
Uc=πa2σεB=πa2Bσ(σ/E+εc)

(9)

对比式(7)和式(9)可知看出，由于徐变变形的存在，外荷载所导致弹性能累积要高于短期荷载。在持续荷载产生的持续变形超过一定程度后，即使此时外荷载保持不变，应变能将超过表面能，导致裂纹开裂并造成材料损伤。为定量化地分析徐变变形对材料损伤的影响，本文定义材料宏观应变能Es=σε。由上述分析可知，在细观层面上，当裂纹尖端应变能到满足下式时，裂纹发生扩展。

σε≥4γ/(πa)

(10)

同时，细观损伤力学认为，当材料内部微裂纹满足式(11)后发生扩展。随着微裂纹的扩展演化，其对混凝土的宏观变形贡献逐渐增加，混凝土应力应变关系呈现出一定的非线性，单轴荷载下混凝土应力应变关系可以表示为

(11)

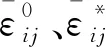
(12)

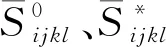
ε*=S(Es)∶σ

(13)

式中：Es为应变能；S(Es)为微裂纹柔度贡献。

以混凝土受压为例，由于混凝土由骨料和砂浆组成，裂纹开始分布在骨料和砂浆的界面上(图3(a))，随着荷载增加微裂纹会发生自相似扩展(图3(b))和弯折扩展(图3(c))，并最终由于微裂纹相互作用形成宏观裂纹导致破坏。由于不同混凝土材料内微裂纹尺寸、分布各异，在外荷载逐渐增加的过程中，不同的微裂纹处于不同的状态，要采用细观力学方法准确计算所有微裂纹对材料损伤、变形的影响非常复杂。

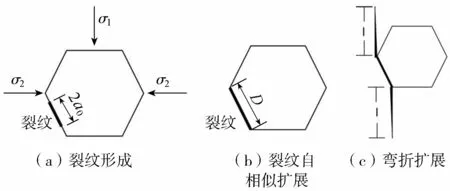
图3 压缩荷载下混凝土内裂纹扩展演化规律

由式(13)可知，只要裂纹应变能σε相同，裂纹扩展状态也相同，微裂纹引起的非线性柔度也相等。因此，本文假设不同荷载历史下，如果宏观应变能Es相等，则材料的非线性柔度张量也相同，这样就可以利用单轴荷载下混凝土的非线性柔度张量来表征徐变荷载下的非线性柔度张量。

首先在单轴荷载下混凝土的应力-应变关系(图4)基础上，根据式(11)获得不同应力条件下的微裂纹产生的应变，然后根据式(13)即可求得非线性柔度张量S(Es)和应变能Es的关系。图4和图5分别为不同强度等级的混凝土应力-应变关系曲线和应变能-非线性柔度张量。可以看出，在相同应变能下，由于低强度混凝土的微裂纹密度更高，因此其提供的非线性柔度张量贡献更大。

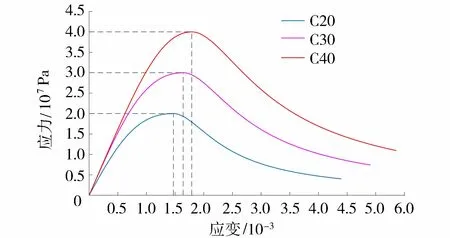
图4 混凝土应力应变关系

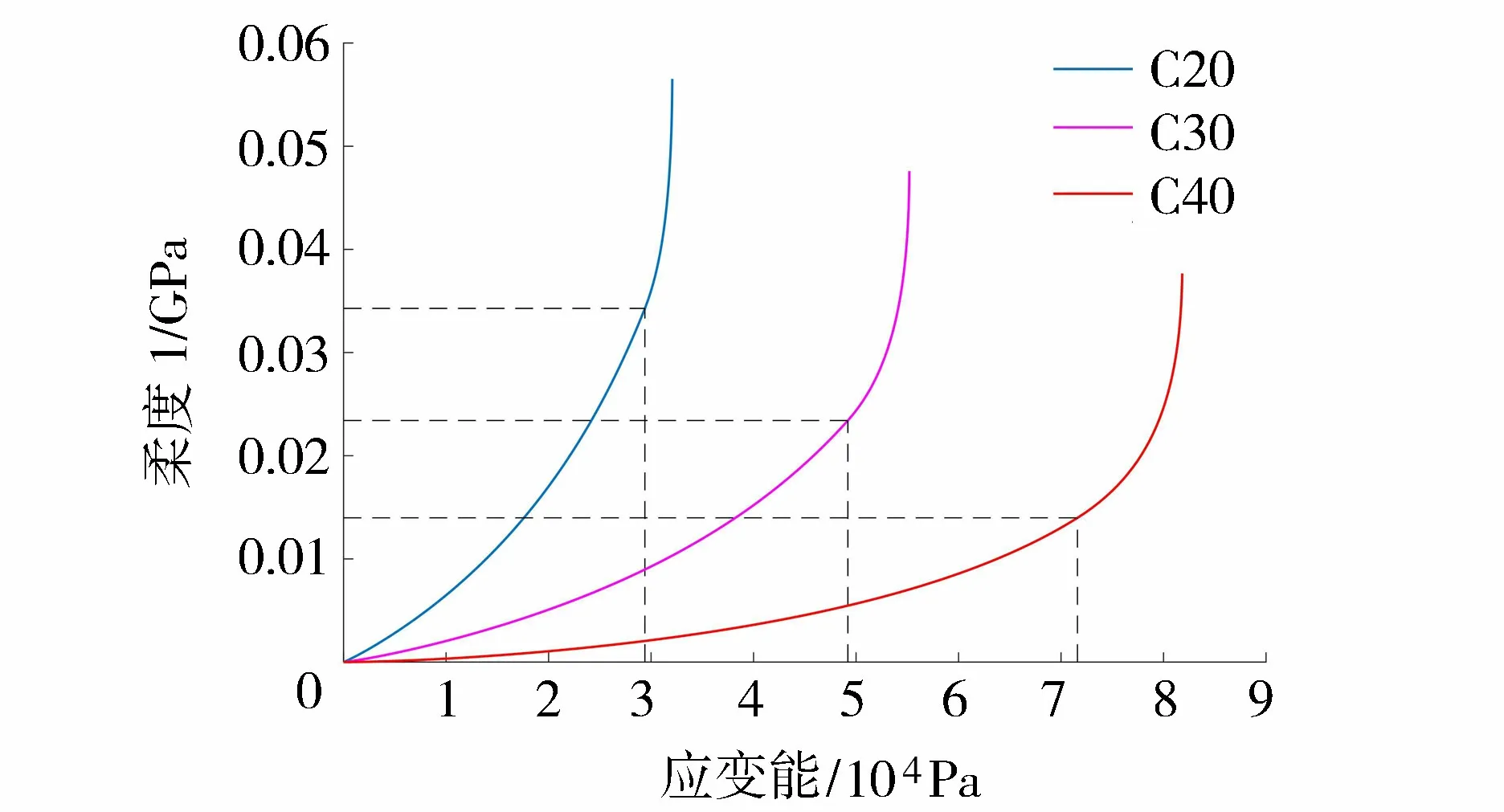
图5 材料应变能-非线性柔度张量关系

基于相同应变能条件的非线性柔度张量等效假设，可以计算持续荷载下混凝土的非线性徐变，建立考虑损伤影响的混凝土徐变损伤模型。在单轴持续荷载下混凝土损伤应变为

(14)

式中：S(Es)为微裂纹柔度贡献，可以通过单轴混凝土应力-应变关系获得(图5)。将式(14)求导后联合式(4)代入式(2)，即可得增量形式的持续荷载下混凝土徐变模型：

(15)

从式(15)可以看出，当持续荷载水平很小时，混凝土为线弹性材料，柔度S(σεtot)和导数S′(σεtot)均为0，此时为线性徐变；当持续荷载水平较高时，S(σεtot)和其导数S′(σεtot)迅速增加(图5)，混凝土的应变增长速率增加，徐变呈现出非线性；当持续荷载水平更高时，在混凝土非线性徐变发展过程中，当应变累积到一定程度后，σ2S′(σε)/E→1，混凝土的应变增长速率趋于无穷大，dε/dt→∞，材料不能继续承受持续荷载，混凝土发生徐变破坏。同时从图5可以看出，混凝土非线性徐变特性和柔度S(σεtot)直接相关，在相同应变能下，强度低的混凝土柔度更高，因此在相同徐变变形影响下，混凝土材料的损伤程度更大，导致混凝土徐变的非线性程度越高。

需要指出的是，由于水泥基材料水化过程比较漫长，混凝土在龄期作用下其强度会逐渐上升，强度随龄期变化会影响混凝土的徐变特性。因此，本文采用CEB-FIP规范[3]推荐公式考虑混凝土强度随龄期的增长规律：

(16)

其中fct为龄期t的混凝土强度，fc28为28天单轴抗压强度。

3 模型验证和讨论

为验证模型正确性，将模型计算值和现有试验值进行了对比和讨论。在计算中，模型不含其他需通过试验结果测定的参数。不同强度等级下混凝土单轴荷载下的应力-应变关系采用GB 50010—2010《混凝土结构设计规范(2015版)》中的推荐公式：

σ=(1-dc)Ecε

(17)

(18)

(19)

式中：ac为混凝土单轴受压应力-应变曲线下降段参数值；fc,r为混凝土单轴抗压强度；εc,r为与单轴抗压强度相应的混凝土峰值压应变；εc,u为应力应变曲线下降段应力等于0.5fc,r时混凝土压应变；dc为混凝土单轴受压损伤演化参数。计算中上述参数取值如表2所示。

表2 混凝土单轴受压应力-应变曲线的参数取值

3.1 混凝土的非线性徐变

图6为持续荷载分别为20%、35%、55%和65%抗压强度时的非线性徐变和时间关系图，图中分别给出了Roll[23]的试验值和本文模型的计算值，试验均为强度等级C30试件，模型计算参数也采用上述规范中C30混凝土应力应变关系计算。

图6 中、低持续荷载下模拟值与试验值对比

从图6中可以看出，计算结果与试验结果吻合较好，所提出的非线性徐变计算方法可以较好地模拟持续荷载下的混凝土徐变变形。需要说明的是，本文提出的计算方法不含任何待定参数，仅仅通过材料在单轴荷载下应力-应变曲线，获取混凝土不同应变能累积状态下的柔度，即可计算混凝土在不同水平的持续荷载下徐变变形性能，适用性较强。

3.2 非线性徐变系数

采用同样的方法可以计算C20、C40和C60混凝土的非线性徐变系数，如图7所示。

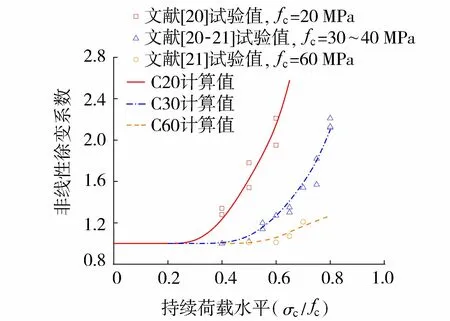
图7 非线性系数与持荷水平关系

从图7中可以看出，通过该方法计算得到的非线性徐变系数与试验值吻合较好，并能够反映出不同强度等级之间非线性系数的区别。混凝土单轴强度越高，非线性徐变系数越小。这是因为混凝土强度越高，微裂纹密度相对较低，在相同荷载水平下损伤较低，在单轴应力-应变曲线上体现出较弱的非线性，在相同徐变荷载下，混凝土损伤程度以及徐变和损伤的耦合影响也较低，因此非线性系数较低。

3.3 混凝土非线性徐变临界点

线性徐变和非线性徐变的界限对结构长期性能分析也很重要，因此在此计算了不同强度等级混凝土的非线性徐变临界点，如表3所示，表3还给出了已有文献中的非线性徐变临界点的试验或经验值。需要说明的是，本文提出的模型没有人为区分线性和非线性徐变，当线性徐变与非线性徐变之差超过5%时，材料的非线性特性较为突出，因此在计算中认为非线性和线性徐变差别超过5%时，此时的徐变为非线性徐变。

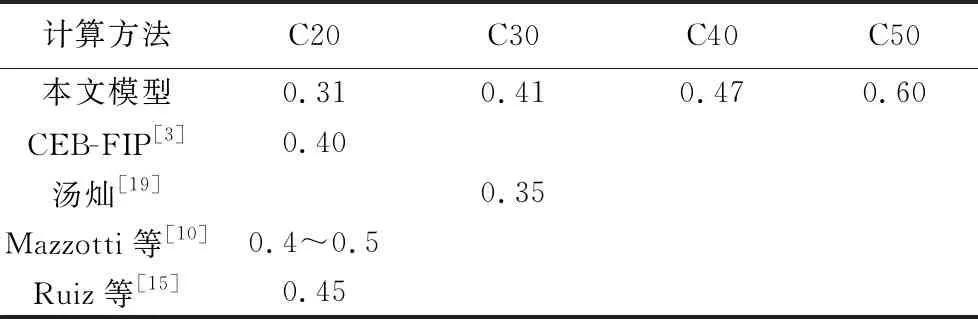
表3 不同强度等级凝土的非线性徐变临界点

从表3中可以看出，本文模型计算与试验值吻合程度较高，模型可以较好地反映混凝土材料从线性徐变到非线性徐变过渡过程，同时本文的模型能体现出不同等级混凝土非线性临界点的差别。从表3中还可以看出，混凝土强度越高，非线性徐变临界点越高；对于C20和C50的混凝土来说，当受到的持续荷载应力分别超过31%和60%的混凝土单轴强度时，徐变才会体现出非线性。