基于二端口散射参数的CVT宽频暂态模型

潘 飞，穆 舟，刘 浩，王彤彤，江 波,张 榆，张晨萌，谢施君，林国松

(1.西南交通大学电气工程学院，四川 成都 611756；2.国网四川省电力公司电力科学研究院，四川 成都 610041；3.清华大学电机工程与应用电子技术系，北京 100084；4.山东泰开互感器有限公司，山东 泰安 271000；5.国网四川省电力公司计量中心，四川 成都 610045)

0 引 言

电压互感器是电力系统中必不可少的测量设备，其将一次系统和二次系统电气隔离开，以便在二次侧对系统进行测量和保护等工作。目前，国内外电力系统大量投入使用的电压互感器主要包含电磁式电压互感器和电容式电压互感器两种。其中电容式电压互感器(capacitive voltage transformer，CVT)由于其绝缘强度高、不易发生铁磁谐振且价格较低等优点被广泛运用于110 kV以上的电网中[1]。

在研究过电压保护问题时，暂态过电压包含丰富的非工频频率分量，而之前广泛运用的CVT在线监测系统不能满足非工频暂态电压的CVT的宽频测量。因此CVT宽频模型的建立一直是众多学者专家研究的重点。准确的CVT宽频模型的建立对于雷电过电压、操作过电压的测量和电磁兼容问题有着重要的意义。

1 CVT的宽频模型

如图1所示,CVT主要由电容单元和电磁单元两部分组成。其中电容单元主要由高压电容C1和中压电容C2串联组成。电容单元将高电压电压波形转换为10～20 kV中压电压波形输入电磁单元。电磁单元由中间变压器、补偿电抗器L、阻尼器D、避雷器BL等组成。为了减小负荷对中压电压的影响，电磁单元的中压侧接入一个补偿电抗器,其在工频电压下与电容单元的中压点阻抗谐振。

图1 CVT稳态物理模型

图1所示的模型为CVT的稳态物理模型。该模型能够准确地体现工频电压下CVT的工作情况。而具有高频成分的暂态电压还将受制于CVT内部复杂的杂散参数以及元件之间的耦合等效应。由于传统的CVT稳态物理模型无法囊括这些效应，因此需要构建新的CVT宽频暂态模型来反应CVT的暂态电压传递特性。

采用图2所示的π型黑盒模型来构建CVT宽频暂态模型。

图2 CVT黑盒模型

CVT黑盒模型由3个子模块构成，子模块内部均由传统的R、L、C元件构成。整个模型基于准确测量得到的端口宽频参数来构建，而不必得到物理模型中各个元件的准确参数。

CVT的π型黑盒建模的步骤如下：

1)测量待测件端口之间的宽频二端口散射参数(S参数)，并转化为二端口导纳参数(Y参数)。运用矢量匹配法将Y参数拟合成有理数表达式，并进行端口无源优化。

2)基于二端口Y参数，计算各个子模块的单端口导纳参数的有理数表达式。

3)基于各个子模块的导纳参数的有理数表达式，进一步用电路综合理论建立等值电路模型。

2 CVT二端口宽频参数的测量与计算

2.1 宽频参数的获取

首先运用网络分析仪测量CVT输入、输出端口的二端口S参数。如图3所示，二端口S参数的4个子参数分别代表着在功率归一化后，两个端口各自的反射参数与两个端口之间的传输参数，可分别用式(1)计算。

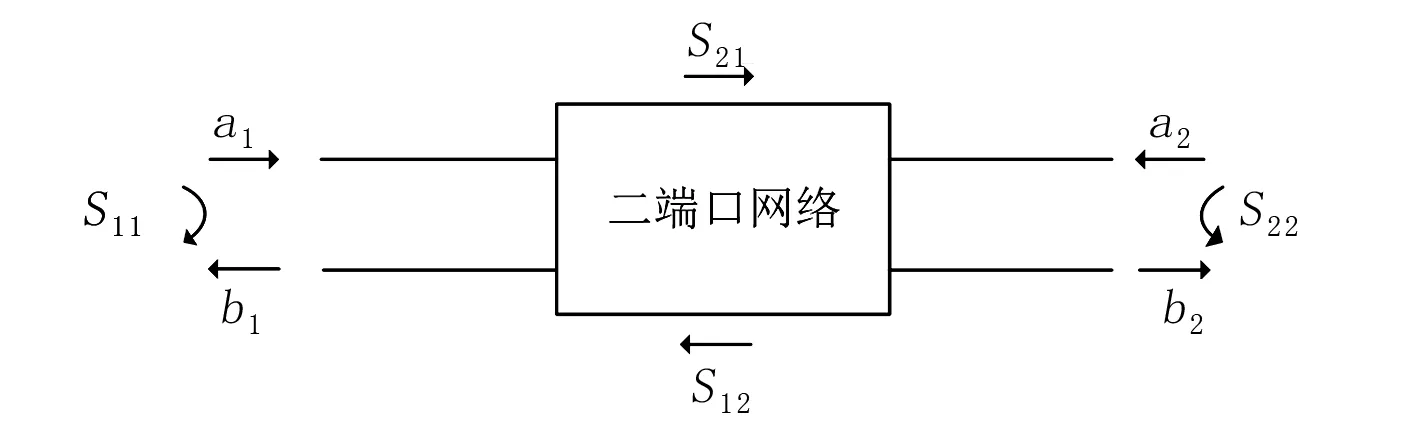
图3 S参数

(1)

图4 AGILENT E0571C对CVT的测量

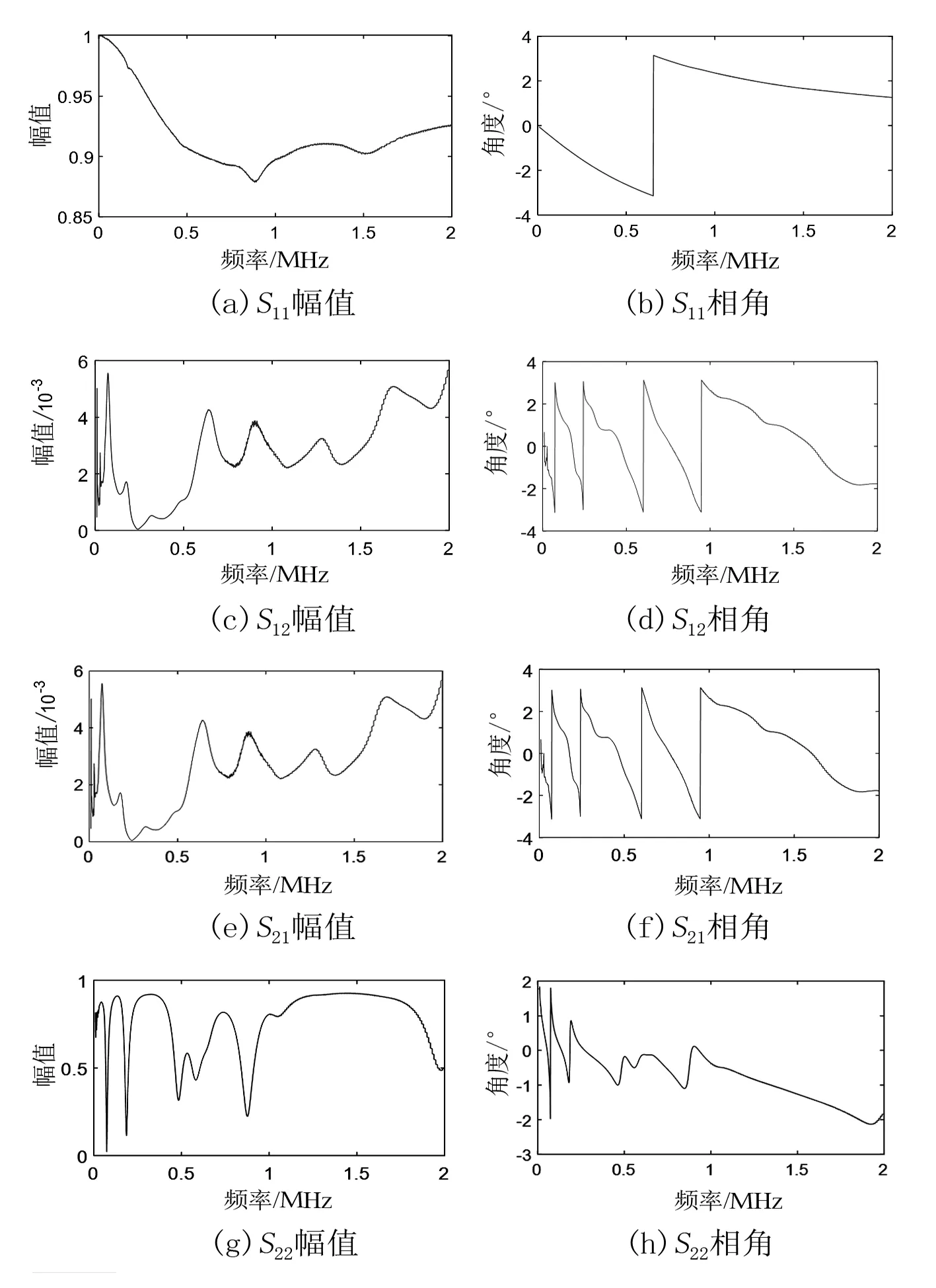
图5 S参数测量结果

获取S参数后，运用式(2)[2]将S参数转换为CVT的Y参数。其中Z01、Z02为端口匹配阻抗，由于实验中使用的同轴电缆以及各端口的特征阻抗均为50 Ω，因此端口匹配阻抗也取50 Ω。

2.2 Y参数的矢量匹配拟合和无源优化

对于上一步获取的一定频率范围内CVT二端口Y参数，其必须拟合为有理数表达式才能进一步地处理。这里采用矢量匹配法对Y参数进行有理数表达式拟合。

矢量匹配法[6-8]是一种能快速收敛且能保持函数稳定性的有理函数拟合方法，由B.Gustavsen于1999年提出。矢量匹配法简洁、快速、稳定且无数值病态问题，被广泛运用于宏模型提取方法和频域线性系统拟合等方向。矢量匹配法将上面测量得到Y11、Y12、Y21、Y22进行有理数拟合，分别表达为如式(3)的有理数分式和形式：

(3)

式中：留数ci和极点ai为实数或共轭复数对；而常数项d和比例项e为实数且为可选项，这里忽略，即e=0,d=0；N为总支路数。

这样矢量匹配的问题就转化为如何得到式(3)中各项系数的估计值来求得f(s)的最小二乘估计。由于未知极点ai在分母，则式(3)对未知数来说是非线性求解问题。矢量匹配法通过引入初始极点将非线性求解问题分解为两步连续的线性问题来求解。

对测得的S参数进行矢量匹配的结果如图6和图7所示，匹配的误差在10-4以下，表明匹配的结果较为精准。

图6 幅值匹配结果

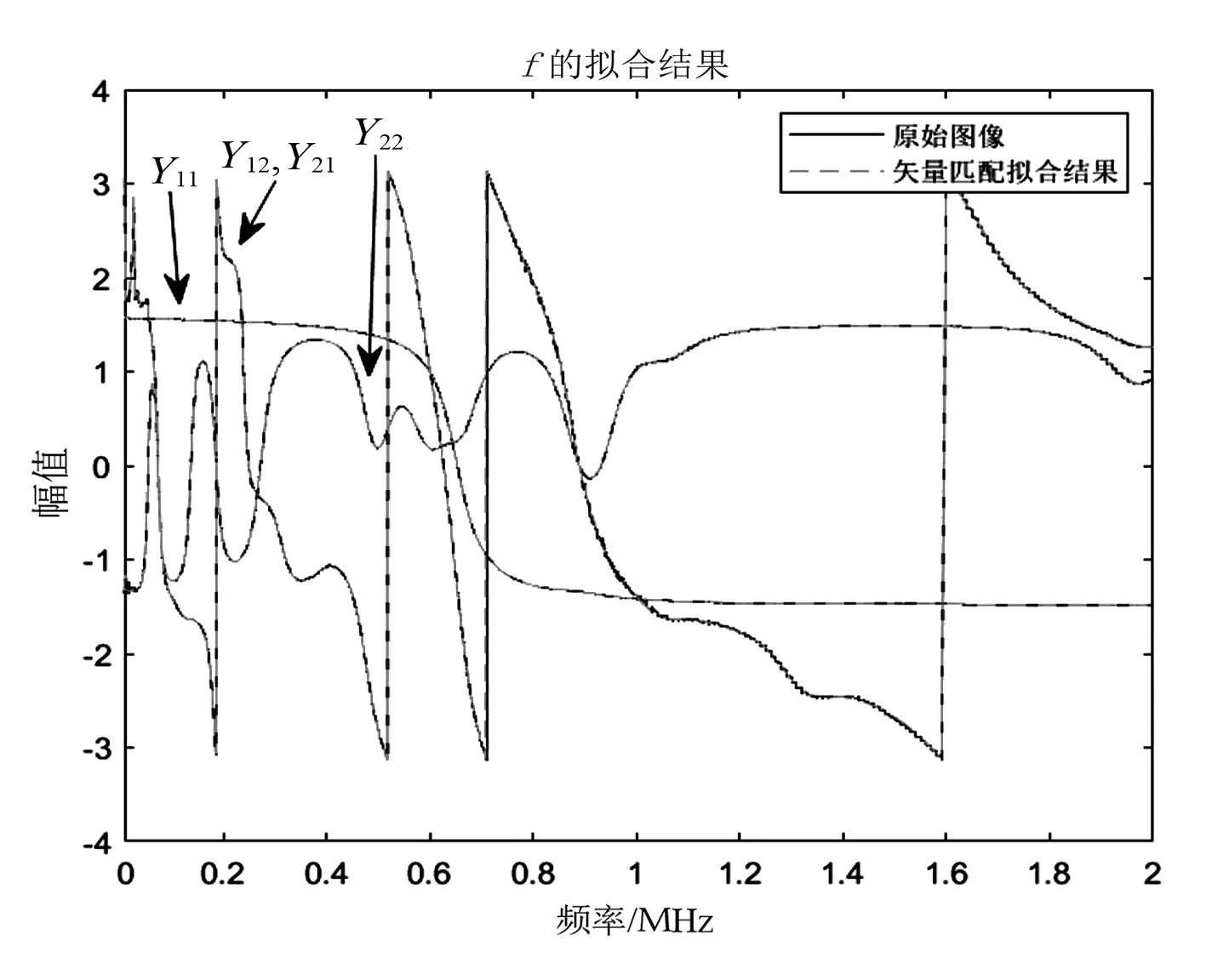
图7 相角匹配结果

矢量匹配法能够保证拟合结果的稳定性(极点实部小于0)，但是无法保证其结果的无源性。而有源的模型也会导致模型的计算结果出现不稳定情况，因此有必要对拟合出的Y参数进行无源优化。

无源性是指一个二端口网络无论在什么端口条件下均不对外产出能量。假设导纳参数矩阵为Y(s)，则电流电压有如式(4)的关系。

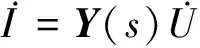
(4)

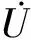
将矩阵Y(s)分解为电导G(s)与导纳B(s)之和的形式，则端口网络吸收的有功功率为

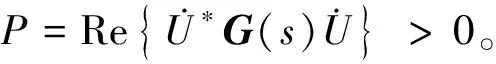
该CVT优化前后的导纳参数特征根如图8所示，可见部分小于0的特征值被优化为正值，从而保证了端口的无源。

图8 对导纳参数的无源优化

2.3 模型的电路实现

基于上一节获得的无源优化后的二端口Y参数的有理表达式，可用式(6)计算如图2所示的π型电路中每个子模块的单端口Y参数有理表达式。

在获取3个子模块的单端口Y参数有理表达式后，根据福斯特II型电路综合理论进行等效电路构建。具体地，每个子模块的表达式可以化为式(7)所示的福斯特部分分式和表达式[10]。

(7)

图9 常数项等效电路

对于实数极点项，可综合表示为如图10所示的RL支路，其值如式(8)所示。

图10 实数极点项等效电路

对于复共轭极点项，可综合表示为如图11所示的RLCG串并联支路。

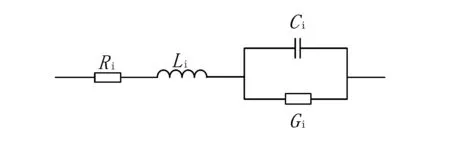
图11 复共轭极点项等效电路

图中各元件的值如式(9)所示。

将上述各个电路并联即可形成子模块的等效电路。则整个π型电路如图12所示，模型即建立完成。

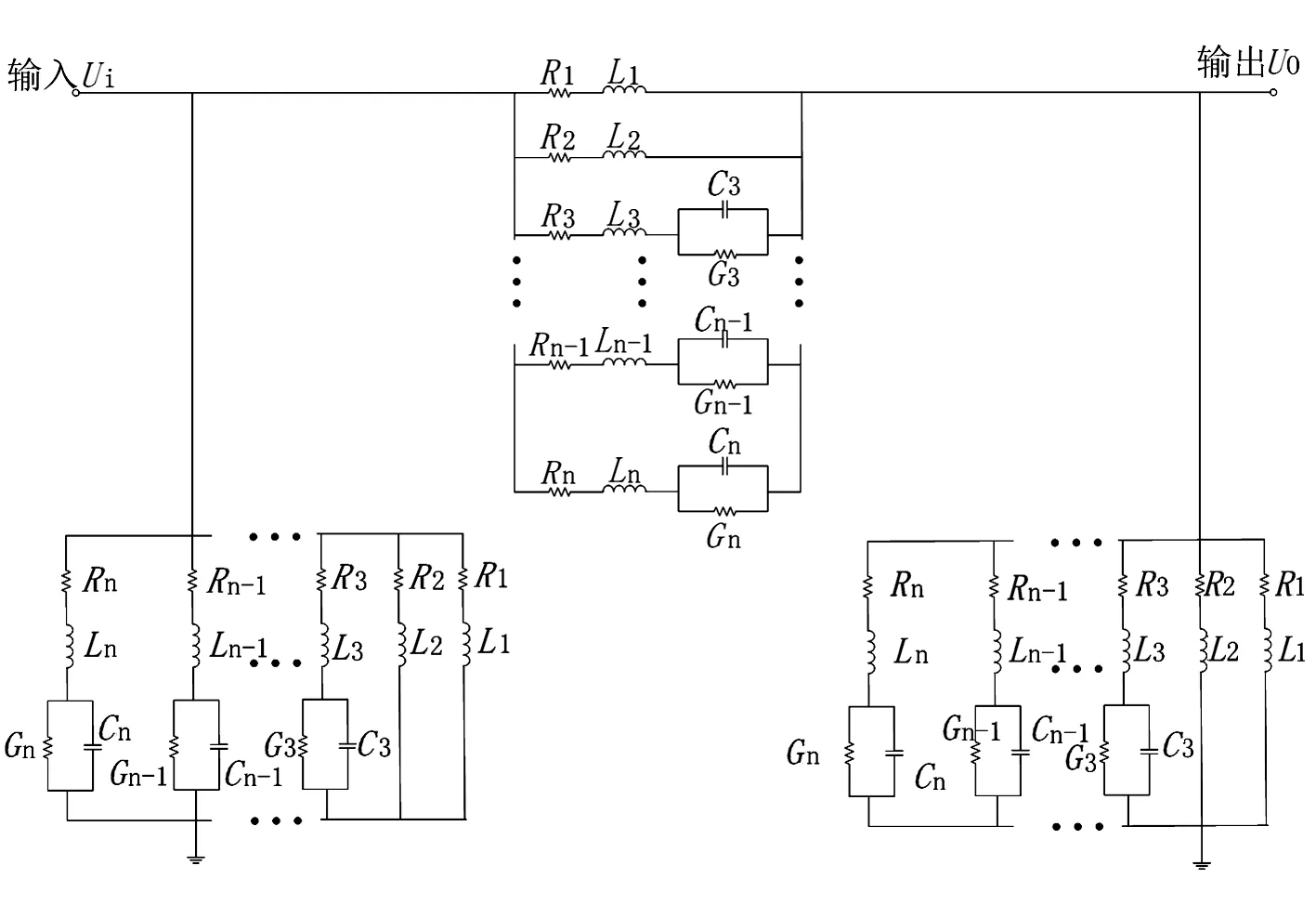
图12 电路综合后的黑盒模型

2.4 模型的计算与验证

为了证实模型的正确性，在测得CVT输入雷电冲击波形Uin的情况下通过电路综合后的黑盒模型计算得到CVT二次侧输出Uout并与实测值对比。

针对图12中的储能元件，采用贝杰龙法对其进行处理[11]。电感和电容可分别将其等值电路表示为如图13所示的形式，图中的IL(t-Δt)和IC(t-Δt)是电感和电容的历史电流值。

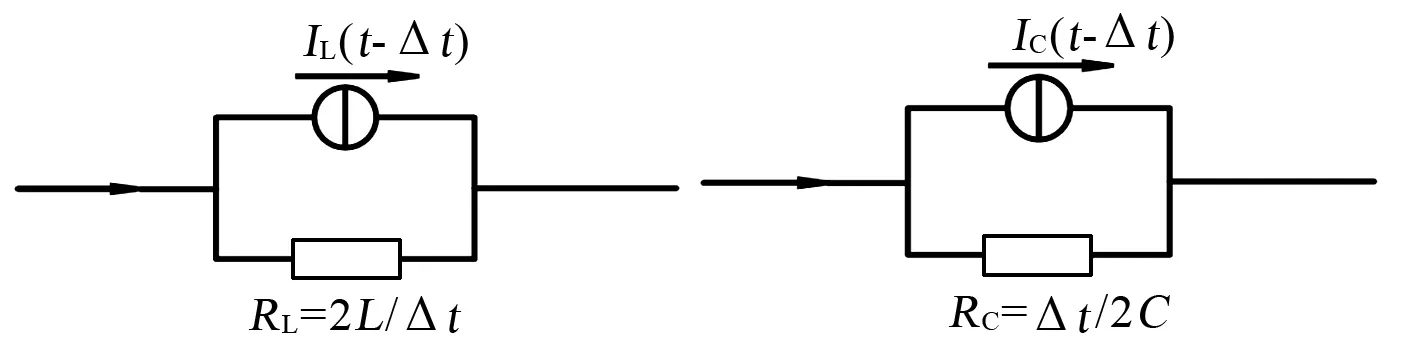
图13 电感、电容等值电路

在S参数的测量完成后，不改变CVT的任何配置，对其进行雷电冲击实验。雷电冲击实验采用实验用雷电冲击发生器对CVT输入200 kV的标准雷电冲击波。

首先，将CVT的所有n端良好接地，所有二次侧端口均开路。将标准雷电冲击发生器的输出端与CVT高压输入端口相连，CVT二次侧端口1a—1n通过1000∶1的衰减器后接入示波器。雷电高压波形通过与CVT并联的129 700∶1的标准阻尼式电容分压器输入示波器。 CVT输入的高压雷电波形如图14所示，实际峰值约为209 kV。

图14 高压标准雷电波形

将测得的高压标准雷电波形带入所述的支路电流法电路矩阵中，计算得到各时刻CVT二端口输出情况，与测量的二次侧波形进行对比，如图15所示。

由图15可看出，计算得到的波形和实验测得的CVT输出波形基本一致。

3 结 语

上面利用二端口散射参数、黑盒模型构建了π型CVT黑盒模型，利用矢量匹配法、宏观无源化和福斯特II型等效电路建立了π型等值电路的CVT模型。为了验证该模型是否能够在宽频暂态电压的条件下表征CVT的端口特性，通过网络分析仪测量CVT的S参数，得到π型等值电路的CVT模型的各个元件参数后，对CVT进行雷电过电压试验，在已知CVT高压输入雷电波形的情况下利用支路电流法列写方程，计算得到CVT二端口的输出波形。最终比较计算波形和测量得到的波形，二者近似相同，验证了所建立的CVT宽频暂态模型的正确性。