为学子们的课堂创造力“推波助澜”——初中数学复习课的习题改编与巧用

张水平

(浙江省嘉兴市海宁市紫微初级中学 浙江嘉兴 314400)

近几年，我国教育领域不断进行改革，其中心和主题是全面倡导和推行素质教育，培养适应新时代需求的创新型人才。素质教育相对传统教育而言，更注重挖掘学生的潜能，让学生全面发展、主动发展、可持续发展，其核心就是培养学生的创造力。那什么是“创造力”呢？创造力是人们根据一定目的，对已积累的知识和经验进行科学的加工和创造，由此产生新认识、新知识，创造出新事物的一种能力。如何打造一个具有活力的初中数学复习课，让学生灵活运用所学的单元新知识进行创造，对习题进行自编自导，自给自足，从中让所学的知识得以巩固和升华？以下是我在探索过程中总结出来的几点浅显认识[1]。

一、课堂上实施创造教育的原则和方法

“机会只会给有准备的人”，任何变革，都是在曲曲折折中迂回前进的过程，想要成功，没有之前大量的充分准备，没有之前的仔细推敲与斟酌，永远不可能一蹴而就。课堂上实施创造教育，要遵循一定的原则和方法。

（一）细心呵护学生的好奇心和想象力，让创造成为可能

爱因斯坦曾说过：“想象力远远比知识更重要，因为知识是有限的，而想象力几乎概括了这个世界的一切，它推动技术进步，它甚至是知识的源泉。”试想，如果没有人类自古以来“上天入地”的想象，怎么会有今天的“嫦娥奔月”和“海底隧道”？所以。好奇心和想象力是进行创造的前提条件，我们要保护好学生以生俱来的想象力，就要给学生营造一个相对宽松的氛围，解放学生的脑、手、嘴，即让学生有内容可以去想象、让学生有条件可以亲自动手去实验和验证、让学生能大胆说出自己的猜想和实验总结等。哪怕学生得出的总结是有缺陷的、甚至是不对，我们也不能立马就否定，“一棍子”就有可能打死了学生一辈子的探索积极性。我们首先得承认学生想象得好、敢于想象，再提出老师对学生这个结论的疑问，接下来老师和学生一起再来进行猜想和验证，以此拉近教师与学生之间的距离，从而达到保护学生的创造精神的目的。

（二）建立学习协作共同体，使创造活动在组内得以共鸣并获得其他成员的支持

一个人的力量是很有限的，人多点子也就多。协作共同体是指为了完成某一特定的任务，学习者之间相互协作，一起进行探讨、交流、实验、验证等活动的一种学习方式，是培养学生自主探究、相互合作、并主动获取数学知识和能力的一个重要途径。课堂创造开展之前，教师必须对学生的协作共同体进行明确的分组和分工，使创造活动有序开展。有时在创造中一个明显错误的猜想，在协作共同体内很快就被否决掉了，省去了教师审核时在时间和空间不足上带来的局限。而有时一个很有挑战意义的猜想，能让学生的意志转化上升成协作共同体的意志，使创造活动在组内得以共鸣，并获得其他成员的支持，大家齐心协力，一起致力于对同一事物的探究。

（三）耐心鼓励学生进行创造，切实转换学生和教师的课堂主体地位

很大一部分孩子还没有要迫不及待地去阐述自己观点的那种自信，更没有在课堂上有跃跃欲试的表现，因为他们习惯了课堂上老师的滔滔不绝，一下子转变了课堂的主体地位，会让孩子有些不知所措。这就需要我们耐心的引导，鼓励他们把心里的想法大声说出来。刚开始进行探索创造的速度可能会慢一些，甚至会出现一节课的任务完不成的情况。但以生为主体的课堂学生需要一个适应期，只要学生习惯了这种让“我”来说的模式，速度也能不断提上来，关键是我们绝对要做到耐心二字，不能一着急就不愿意听学生那曲折的探索过程，自己代替学生一股脑儿就全说了。只有让学生亲自去创造，亲自去走一走“弯路”，才能让学生对知识的理解更加透彻，才能让学生有我也能解决问题的感觉，从而提升他们的学习自信心。

二、实施创造教育的过程

课程改革的今天，数学复习课早已不是“机械练习”加“疲劳训练”的苦干、蛮干，而是巧干加巧练。教师虽然已不再处于课堂的主体地位，但教师仍是课堂的掌舵人、主持人。掌舵人指向哪，学生才能有前进的方向和目标。教师从某个点出发，根据某一关键词或关键点，提出质疑或创造的方向，让学生以此展开想象，进行创造。创造的类型有很多种，具体可以根据创造的内容来确定类型需求[2]。

（一）串联型创造

串联型是指把某一领域的知识点串联起来，是层层递进的关系，简单的改编或自创习题后，能用这个习题进行一系列知识点的再现与复习。这种方法能将原本简单的知识点的罗列变成结合实际问题后的知识点一一再现并得以使用。例如，复习特殊三角形时，我们复习到直角三角形一课。课上我们并没有直接一一罗列与直角三角形有关的一些性质定理和判定定理，而是这样引导学生进行复习的[3]。

师：同学们，看到直角三角形，你们觉得它的什么内容比较重要？

有学生开始抢答：直角三角形的勾股定理。

师：很好，那你们能编一题与勾股定理有关的题目来考考大家吗？

刚抢答学生所在的协作共同体内的成员马上行动起来了，自创一题：（图一）已知Rt△ABC中，∠C＝90°，BC＝6，AC＝8，求AB的长。

师：很好，其他的协作共同体能具体说说怎么解决这个问题吗？

……

等这题勾股定理知识点的运用一解决，教师又继续引导。

师：其他协作共同体觉得直角三角形的什么内容比较重要？

又有一协作共同体的同学思考并说出了想法，

生：直角三角形斜边上的中线等于斜边的一半这个知识点比较重要。

师：非常棒，那么你们能在刚才那个题上加上这个知识点，同时用两个知识点来考大家吗？

所有的协作共同体都在一起商量，思考怎样把这两个知识点串起来。

很快学生便有了各种各样的串联方法。

某协作共同体给出的问题是：（图二）已知Rt△ABC中，∠C＝90°，CD是斜边上的中线，DC＝5，AC＝8，求BC的长。

某协作共同体：老师，我们觉得用一条边上的中线等于这条边的一半的三角形是直角三角形来判定直角三角形也很重要，看书本上有这个证明。我们为此创设了这样一题：（图二）△ABC中，CD是AB边上的中线且等于AB的一半，DC＝5， AC＝8，求BC的长。我们这个题把三角形三个内角之和等于180°、一条边上的中线等于这条边的一半的三角形是直角三角形、勾股定理三个知识都串联了起来。

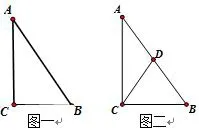
大家一听，一时之间都没反应过来，因为没啥反响。于是，我让这个协作共同体内派一名代表具体说说三个知识点是怎么用的。原来在证明一条边上的中线等于这条边的一半的三角形是直角三角形时运用了三角形三个内角之和等于180°这个知识点。这个代表一说完，没等我开口，教室里已经掌声雷动。显然，这个协作小组的创造，赢得了大家的赞同，我也跟着鼓起掌来，以此表达我对他们的“伟大创举”的肯定。通过对这个习题的改编，大家了解了改编者的出题意图，也明白了这个习题的解决方法，不知不觉中已经复习了直角三角形的很多个知识点，整个过程不直白、不单调[4]。

（二）并联型创造

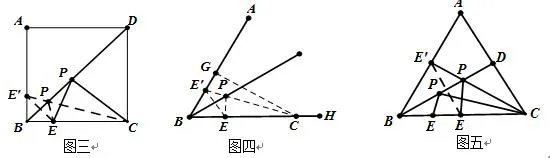
这时我又要追问了，那可不可以把∠ABC=60°改成别的度数？同学们又津津乐道地把60°改成了45°、30°等特殊角来进行计算。正当他们得意的时候，我又来了一句：前面都只有一个不确定位置的动点P，如果点E也是动点，你还能解决这类问题吗？在好奇心的驱使下，同学们又合作出了图五：已知等边三角形△ABC的边长为4，P是∠ABC的角平分线上的一点，E是边BC上的一个动点，求PE+PC最小值。此题一出，很多同学都表示不会做，可能题目出得有问题。我鼓励学子们：不动手试试，怎么知道不会做呢？它和前面的题唯一不一样的地方就是点E的不固定，多试试几个E点的不同位置，就能用我们的双手来创造奇迹哦！协作小组考虑了几种E点的不同位置，发现求PE+PC的最小值即求E′C的最小值，而E′是由E点关于BD对称后的点，始终在AB边上，于是求E′C的最小值问题就转化成了求AB外一点C到AB的最短距离，大家发现问题迎刃而解了，只需作CE′⊥AB，求出等边三角形的高，就是PE+PC的最小值。

随着大家一个个问题的提出和解决，达到了复习的目的。情绪上适度的紧张和愉悦，也让学子们体会到了思绪参与的重要性，也为学子们打开了创造思维的大门。有时课外都还会有惊喜，学生把课堂上老师没展示的题，拿来给老师“鉴定”，以证明自己的协作小组也是非常棒的。学生也在创造中渐渐地产生了学习的自信心[5]。

三、创造的反思与总结

人类之所以能不断进步，在于人能不断总结与反思，找出某一类事物的规律，并且运用这个规律，提高解决问题的能力和效率。

也正因为有了复习课上学生创造了一个又一个惊喜，让我有着意想不到的收获，课堂上的师生都充满了幸福感，让我一直庆幸自己在复习课上给了学生进行创造的时间和空间，让他们的天赋得以展示，让他们又重获了学习的自信！