一题多解在中考复习中的应用与思考

信琴琴

(华中师范大学厦门海沧附属中学 福建厦门 361026)

在第一轮中考复习中，所有学生主要以落实基本知识和基本技能为主，但学有余力的学生要能构建初中数学的知识体系，并且理清知识之间的联系。以相似三角形和锐角三角函数为例，人教版教材将锐角三角函数放在相似三角形之后，这两者之间的共同之处都是求线段的比值问题，但锐角三角函数是利用相似的直角三角形得到的，所以可以看作相似的一个特例，从本质上讲，它也可以看作是相似问题。为了通过题目使学生更加清楚这两者之间的关系，需要教师认真选题，并认真研题，通过解题析题过程，让学生以后遇到线段的比值问题时能够快速确定解题方向和策略。

一、题目选取

（2020福州二检）已知△ABC，AB＝AC，∠BAC＝90°，D是AB边上一点，连接CD，E是CD上一点，且∠AED＝45°.

（1）如图1，若AE＝DE，

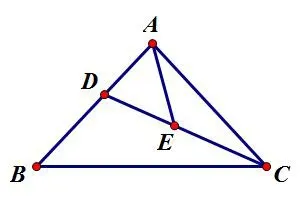
图1

①求证：CD平分∠ACB；

（2）如图2，连接BE，若AE⊥BE，求tan∠ABE的值。

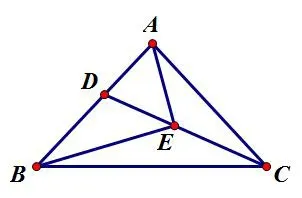
图2

二、了解问题

本题在等腰直角三角形的背景下，已知一个特殊角，问题（1）中增加线段相等的条件，要求证CD平分∠ACB，同时还要求线段的比值，如何寻找本题的突破口？这些条件该如何使用？

问题（2），改变条件，若AE⊥BE，求tan∠ABE的值。而我们知道解题的关键求出AE和BE之间的关系。

三、拟定计划，实现计划

因为已知△ABC，AB＝AC，∠BAC＝90°，故∠B=∠ACB=45°。

对问题（1），根据已知条件，∠AED＝45°，AE＝DE，则∠EAD=∠ADE=67.5°。

①求证：CD平分∠ACB。只要想办法证明∠ACD=∠CAE即可解决问题。

解法1：利用外角，因为∠ADE=67.5°，∠B=45°，所以∠ACD=22.5°，因此∠CAE=22.5°，解决问题。

解法2：利用直角三角形两锐角互余，因为∠BAC＝90°，∠ADE=67.5°，所以∠ACD=22.5°，得证。

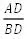
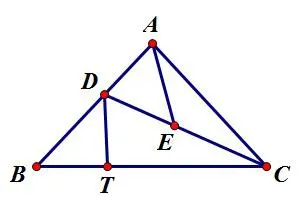
图3

分析：根据①中CD平分∠ACB的结论，联想到角平分线的性质，尝试解决问题。学生能利用角的平分线的性质，证明与线段相等有关的问题。这里可以考查学生运用角平分线的性质解决几何问题的能力，以及对添加的辅助线的掌握情况。

除了这种方法，你能尝试用其他方法解题吗？可以试试看。这样的设问可以拨动学生的好奇心，激发数学学习的原动力，尤其是初三学生，已经储备了很多知识，当然跃跃欲试，并且往往会收到较好的效果。学生会发现数学开始变得“好玩”起来。很快就会有其他做法。

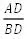
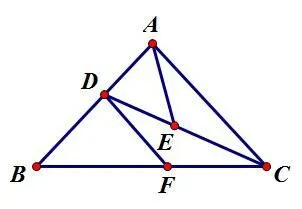
图4

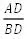
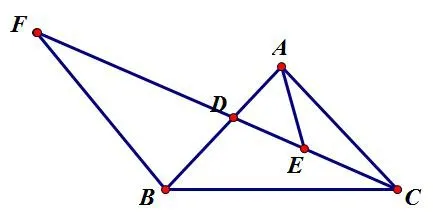
图5

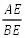
解法1：三角形相似

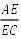
图6

解法2：构造手拉手模型

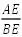
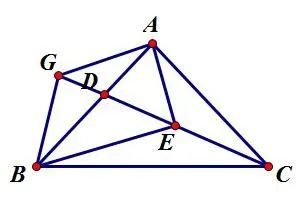
图7

解法3：构造弦图模型

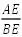
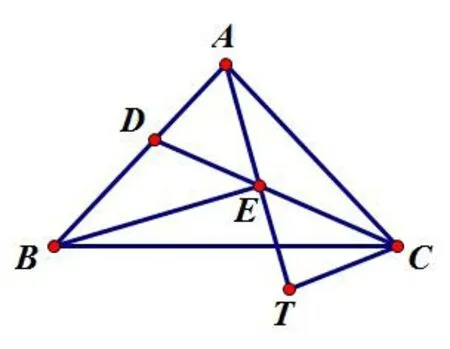
图8

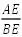
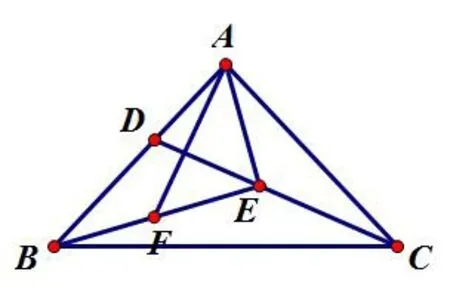
图9

综上，求线段比值的问题时，我们常借助相似三角形或者锐角三角函数，如何构造值得思考。通过解题、析题的过程，最后让学生感悟，可以添加平行线，构造“8字型”形似或者“A字型”形似；或者作垂线，构造直角三角形，达到解决问题的目的。

此外，通过解题析题过程，让学生进行归纳总结，遇到求线段比值问题的题目时，可以通过添加辅助线（平行线、垂线等），构造相似三角形或者直角三角形来解决问题，达到多题一解的目的，使学生明确解题方向。

四、回顾反思

教师不能单纯地搞题海战术，我们首先要明确所选例题要使学生掌握什么知识，明白什么知识之间的关系，以学生为主体，从学生的认知角度出发，然后引导学生进行数学思考，搞清楚知识的来龙去脉，并不断让学生总结各类问题的解题策略和思路及所用到的知识点，通过思考，发现问题，进一步反思，真正感悟到例题所发挥的价值，以发展学生的创新意识和应用意识。

在解题过程中，我们不断引发学生进行思考，让学生充分思考，确定不同的解题的方向，则能使不同的学生得到不同的发展。在教学过程中，教师应认真钻研教材和题目，并且尝试从多个进行解题，进而引导学生尝试用多种方法解题，且对各种方法进行对比归纳，以此拓展学生的思维，提高学生分析问题和解决问题的能力。

五、教学思考

（一）提炼基本模型，引导方法选择

在平时的习题教学过程中，教师不能单纯为了讲题而讲题。在每节习题课前，要认真钻研教材和题目，引导学生从多个角度寻求解题思路，并制定相应的计划进行尝试，在尝试过程中，让学生感悟解题方向对解题的影响，培养学生发现问题、分析问题和解决问题的能力。通过这种引导，可以改善学生的数学学习方式，使学生的思维得到提升。最后，还要对题目进行回顾，对解题方法和思路进行归纳总结，让学生的学习不再是单纯地解题。

（二）注重一题多解，提高解题技巧和能力

《课标》指出，数学课程要让学生获得适应社会生活和进一步发展所必须的数学基础知识、基本技能、基本思想、基本活动经验。因此，在解题过程中，教师一定要带着学生充分挖掘题目中条件隐藏的信息，分析条件特征和图形特征，通过分离基本图形、基本模型等，寻求突破口，并且要多问问还有没有其他解法。课堂上让学生尽可能展示不同的解题方法和思路，并让学生对比不同方法的优劣，以及在什么条件下选择什么样的方法更佳。通过一题多解的训练，可以使学生在解题思维上更灵活，思路更广，而且能培养学生分析问题和解决问题的能力。

综上，在平时的教学过程中，要以《课程标准（2011年版）》为基本依据，仔细研读教材，精选优选题目，根据学生实际和课标的要求用好教材，用好例题，切实培养学生的核心素养，拓展学生的数学思维。