基于SM2 的多接收方公钥加密方案*

赖俊祚, 黄正安, 翁 健, 吴永东

1. 暨南大学, 广州510632

2. 鹏城实验室, 深圳518055

1 引言

自2008 年中本聪发表题为《比特币: 一种点对点的电子现金系统》[1]的白皮书以来, 作为比特币核心技术的区块链开始快速发展. 从技术应用的角度来看, 区块链可视为一种分布式数据库, 它使用密码学、时间戳和共识算法技术等实现了去中心化的分布式架构. 区块链具有去中心化、可追溯、集体维护、透明开放、无法篡改等特点[2], 这些特点为区块链构建了信任基础, 解决了信息不对称的问题, 使其广泛适用于多用户、多接收方的应用场景. 然而, 如何在一个不依赖任何信任机构、透明开放的区块链系统上对用户关键数据进行隐私保护, 这一问题仍未能得到有效解决. 常规的公钥加密虽然能保证机密性, 但在多接收方的场景下计算成本呈线性增长, 极大影响加密效率. 一种比较合适的解决方案是先采用随机数重用的多接收方公钥加密方案对数据进行加密, 再将密文数据传到链上. 与常规公钥加密相比, 这种加密类型效率更高, 更适合区块链等去中心化、多接收方的应用场景, 能起到更好的隐私保护效果.

多接收方公钥加密最早是由Bellare 等[3]正式提出的. 文献[3] 中指出, 公钥加密的单接收方INDCPA/CCA 安全性可以推出多接收方IND-CPA/CCA 安全性. 随后, Bellare 等[4]提出“可复现的公钥加密(reproducible PKE)” 这一概念, 并指出如果一个可复现的公钥加密方案满足IND-CCA 安全性, 那么以该方案作为底层方案而得到的随机数重用的多接收方公钥加密方案仍满足相应的IND-CCA 安全性(按照文献[4] 中的记号, 称为RR-IND-CCA 安全性).

SM2[5]是我国国家密码管理局推出的一种由我国拥有完全自主知识产权的非对称商用密码算法. 该算法基于椭圆曲线密码体制, 与国际通用的RSA 密码体制[6,7]相比, 在同等安全强度下具有更高的效率.当前我国在金融、政企等要求高安全等级的行业大多采用国际通用的加密算法, 而越来越多的国际通用密码算法被攻击或者被破译, 使得我国的信息安全面临严重威胁. 选择更安全、更高效的国密算法, 或者基于国密算法构造新的加密方案, 在信息安全已上升到国家安全的战略地位的今天, 有着重要的意义.

本文从我国的区块链数据隐私保护研究现状和安全需求出发, 首次基于国密算法SM2 提出了一个随机数重用的多接收方公钥加密方案, 并在随机预言机模型[8]下证明该方案满足RR-IND-CCA 安全性.

本文的其余部分结构如下: 第2 节介绍了ODH 困难假设、IND-CCA 安全性、RR-IND-CCA 安全性、可复现的公钥加密等相关知识; 第3 节研究如何构造随机数重用的多接收方公钥加密方案; 第4 节用椭圆曲线实例化该方案, 由此得到一个基于SM2 的随机数重用多接收方公钥加密方案.

2 预备知识

基本符号. 本文中, 我们统一用κ表示安全参数, 用N 表示自然数集. 对任意n ∈N, 符号[n] 表示集合{1,2,··· ,n}. 对任意有限集S,s ←S表示从S中均匀随机地选取出一个元素s. 若D是定义在S上的一个概率分布,s ←D表示从S中按概率分布D选取元素s. 我们用{0,1}∗表示所有长度的字符串组成的集合, 用{0,1}ℓ表示长度为ℓ ∈N 的字符串组成的集合.

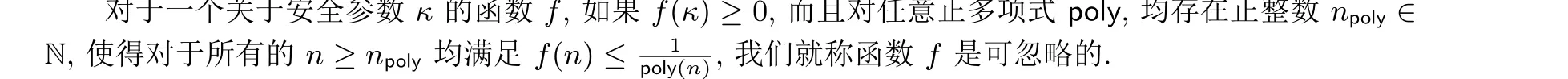
对任意概率算法A, 记A所用的随机数集合为RA.y ←A(x1,x2,··· ,xt) 表示“算法A以(x1,x2,··· ,xt) 为输入, 同时选取内部随机数r ←RA, 最后输出结果y”. 如果A的运行时间是关于安全参数κ的多项式, 则称A为概率多项式时间(probabilistic polynomial time, PPT) 算法.

我们用粗斜体表示向量, 比如m(相应地,m[i] 表示m的第i个分量,|m| 表示m的分量个数,|m[i]| 表示m[i] 的比特长度). 除非特别说明, 否则, 对任意概率算法A,A(m) 均表示算法A对m的每个分量单独作用(每次独立选取内部随机数), 即A(m):=(A(m[1]),A(m[2]),··· ,A(m[|m|])).

Oracle Diffie-Hellman 困难假设. 本文公钥加密方案的安全性将依赖于oracle Diffie-Hellman 困难假设(简记为ODH 困难假设). 我们回顾文献[9] 中的ODH 假设定义如下. 记G为群参数生成算法:该算法以安全参数1κ为输入, 输出一个q阶循环群Gq的描述、q以及Gq的任意生成元g(其中, 要求q的二进制表示是κ比特长的字符串). 简记为(Gq,q,g)←G(1κ). 此外, 记ℓlen∈N,H:Gq →{0,1}ℓlen是一个函数.

定义1 (ODH 困难问题[9]) 如果对任意PPT 敌手A,A的优势

而且要求在这两个实验中,A都不能向Hv(·) 询问gu.

公钥加密. 根据文献[3,4] 的符号标记方式, 一个公钥加密方案PKE 由以下4 个PPT 算法组成:

• PGen: 该算法以安全参数1κ作为输入, 输出一个公共参数par. 简记为par←PGen(1κ).

• KGen: 该算法以公共参数par 作为输入,输出一对公私钥对(pk,sk). 简记为(pk,sk)←KGen(par).

• Enc: 该算法以公共参数par、公钥pk 和明文m作为输入, 输出一个密文c. 简记为c ←Enc(par,pk,m).

• Dec: 该算法是确定性算法, 以公共参数par、私钥sk 和密文c作为输入, 输出一个明文m或符号⊥(表示c不是合法密文). 简记为m/⊥←Dec (par,sk,c).

对任意合法生成的公共参数par, 我们将相应的明文空间记为M(par), 相应的Enc 内部随机数空间记为REnc(par). 公钥加密方案的正确性要求如下: 对于任意par←PGen(1κ), (pk,sk)←KGen(par) 和任意明文m ∈M(par), 有Dec(par,sk,Enc(par,pk,m))=m.

接下来, 我们回顾公钥加密中最常见的一个安全模型: IND-CCA 安全性[10].

记A= (A1,A2) 为带有状态信息的概率多项式时间敌手. 对于一个公钥加密方案 PKE =(PGen, KGen, Enc, Dec), 我们考虑以下实验:是可忽略的, 则称PKE 是IND-CCA 安全的.

随机数重用的多接收方公钥加密. 通常来说, 在标准的公钥加密应用场景中, 每当给一个用户(即接收方) 发送消息, 就需要以该用户的公钥作为加密公钥, 调用加密算法(需要均匀独立随机地选取一个内部随机数) 对消息进行加密. 这就意味着, 每给一个接收方发送加密消息, 就需要一个均匀独立随机选取的内部随机数. 当需要同时给多个接收方发送加密消息的时候, 这种解决方案自然也要求发送方生成多个满足均匀分布的内部随机数用于加密. 为了降低实际应用中随机数生成方面的计算成本并提高效率, Bellare 等人[4]针对多接收方的公钥加密场景提出了随机数重用的公钥加密方案.

3 随机数重用的多接收方公钥加密方案

本节中, 我们提出一个高效的随机数重用多接收方公钥加密方案, 并在随机预言机模型下证明其满足RR-IND-CCA 安全性. 我们将在下一节给出该方案基于国密算法SM2[5]的一个实例化版本.

3.1 方案构造

记G为一个群参数生成算法,ℓmsg,ℓkey,ℓctx∈N. 记H1: Gq →{0,1}ℓmsg×{0,1}ℓkey和H2:Gq×{0,1}ℓkey×{0,1}ℓmsg→{0,1}ℓctx为两个哈希函数. 在本方案的安全性证明中,H2将用随机预言机[8]来替换.

我们的底层公钥加密方案PKE1如图1 所示.

图1 公钥加密方案PKE1Figure 1 PKE scheme PKE1

定理3 PKE1是可复现的.

3.2 安全性证明

本小节中, 我们给出定理2 和定理3 的完整证明.证明(定理2): 我们构造一个针对关于(G,H1) 的ODH 问题的敌手B如下所示.

B收到(1κ,Gq,q,g,U,V,W) 以后, 令par = (1κ,H1,Gq,q,g), pk =V,c∗1=U, (k1,k2) =W, 并将(par,pk) 发给A1.

同时,B给A1提供随机预言机(即H2) 和解密预言机的询问服务.

随机预言机询问方面,B预先初始化一个空表List, 然后通过这个列表来回答A的询问. 具体而言,对于A1的任意一个随机预言机询问x ∈{0,1}∗,B首先检查List 中是否存在元组(x,∗). 如果A1是首次询问到x,B随机选取y ←{0,1}ℓctx, 将(x,y) 存入列表List 中, 并把y作为返回值发给A1; 如果A1不是首次询问到x, 则在List 中必然存有元组(x,∗) (比如, (x,y′)), 这种情况下,B就将y′作为返回值发给A1.

通过这样的方式,B可以回答A2的随机预言机询问和解密询问.

最后,B从A2处收到一个比特b′, 将b′′=(b′=b) 作为自己的最终输出值.

以上就是关于敌手B的描述.

下面我们考虑B的优势.

事件Evt2发生时,A提出的所有解密询问中, 所有不属于TypeI类的询问c= (c1,c2,c3) 均满足c1=且DEC(c) =⊥. 我们注意到, 只有当A提出不属于TypeI类的解密询问时, (k1,k2) 才会在对解密询问的回答中被调用到(换句话说, 在上面事件Evt1发生时, (k1,k2) 只在挑战密文的生成过程中用到, 其他任何时候都不再涉及到). 另一方面, 对任意固定的同时满足c1=和DEC(c)=⊥的解密询问(c1,c2,c3),c1=确保在回答解密询问的过程中需要恢复出(k1,k2), 而DEC(c)=⊥确保最多只有k2被调用来回答该解密询问. 由于(k1,k2) =W ←{0,1}ℓmsg×{0,1}ℓkey, 所以这种情况下从A的角度来看,k1依然是均匀独立随机分布的, 也就是说无论b= 0 还是b= 1,A所看到的元素分布依然完全相同.由此可知,

4 基于SM2 的RR-MRPKE 实例化方案

令a,b为有限域Fq上的元素, 且a,b共同定义了Fq上的一条椭圆曲线E. 记E(Fq) 是E的所有有理点(包括无穷远点O) 组成的集合.G是E上的一个基点, 其阶为素数p. 记h是p的余因子. 对任意k ∈N, 我们用kG表示椭圆曲线上G的k倍点. 记KDF:{0,1}∗×N→{0,1}∗是文献[5] 中指定的密钥派生函数. 对于任意ℓ ∈N, KDF(·,ℓ) 是一个长度为klen 的比特串. 令H是一个哈希函数, 在安全性证明中将用随机预言机来代替.

性能分析. 本文首次基于国密算法SM2 构造了一个随机数可重用的多接收方公钥加密方案, 为了更直观地展现本方案的优势, 我们与基于国密算法SM2 实现多接收方功能的一般的构造方法进行了性能比较. 我们主要从发送方的计算代价和发送方与接收方的通信代价两方面进行性能分析. 假设发送方要给n个接收方发送消息. 在计算代价方面, 如表1 所示, 其中GC、KDF、XOR、H 分别表示倍点运算、KDF函数运算、异或运算和哈希函数运算. 本方案要求发送方在生成n个不同公钥加密的密文的过程中, 只需要选取一个随机数r和做一次倍点运算, 即计算一次椭圆曲线点c1=rG= (x1,y1)∈F2q. 而使用SM2算法构造的一般的多接收方加密算法在生成n个密文给n个接收方时, 需要重复选取n个随机数, 再针对每个随机数做一次倍点运算, 即需要做n次倍点运算. 因此, 与原始方案相比, 本方案能够有效减少发送方的计算量, 提高加密算法效率.

表1 性能分析Table 1 Performance analysis

同时, 我们绘制了在不同接收方数目的情况下的加密算法的计算开销, 如图2 所示. 对比可见, 本方案在加密算法的计算性能上明显比原始方案有优势.

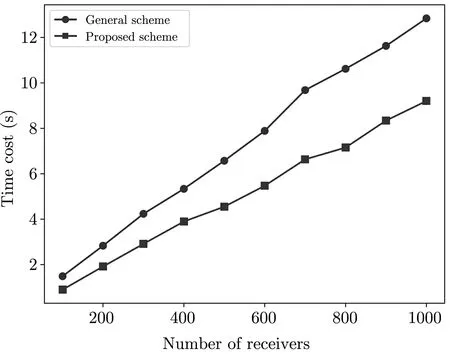
图2 加密计算开销比较Figure 2 Computation overhead comparison of encryption

在通信代价方面, 如表1 所示. 一般的构造方案需要发送方返回n个密文c[i] = (c1,i,c2,i,c3,i),i ∈[n], 而本方案只需要发送方返回密文c=(c1,(c2,i,c3,i)i∈[n]), 与一般的构造方法相比, 减少了|c1|(n −1)bit 的通信量, 其中|c1|=|c1,i|. 在本方案中,c1的长度为128 bit,c3,i的长度为64 bit. 因此, 当消息m的长度为64 bit, 即c2,i的长度为64 bit 时, 本方案可以节省大约1/2 的通信代价. 与原始方案相比, 本方案具有明显的通信优势.

5 总结

本文从区块链去中心化的多用户应用场景出发, 结合我国当前的信息安全需求, 基于国密算法SM2提出了一个随机数重用的多接收方公钥加密方案. 该加密方案不仅能满足区块链多接收方场景下的数据隐私保护需求, 与常规公钥加密方案相比, 还能显著降低加密算法中随机数生成过程的计算成本. 而且, 该加密方案是基于国密算法构造而成, 能更好地满足国内现实应用的安全需求和相关行业监管要求.