差分可辨性隐私参数的迭代分配方法*
2021-09-14任旭杰刘建伟
任旭杰, 尚 涛, 刘建伟
北京航空航天大学 网络空间安全学院, 北京100083
1 引言
随着大数据和云计算时代的到来, 各种数据挖掘算法得到了飞速发展. 例如聚类算法, 通过几轮迭代将一个数据集划分为多个簇, 同一簇中的数据相似性较高, 不同簇之间相似性较低, 以此实现对数据的无标签分类, 可以对数据隐含未知信息进行挖掘, 对大数据的潜在价值有重要作用. 但在聚类为数据带来应用前景的同时, 也出现了一些敏感信息的隐私泄露问题. 近些年, 对隐私保护的研究已成为学术界的热门方向.
2006 年, Dwork[1]提出差分隐私的概念, 具有严格的数学理论基础, 不依赖攻击者的背景知识, 把对敏感数据的保护程度参数化为一个隐私预算值ϵ; 2005 年, Blum 等人[2]在SuLQ 平台上设计实现了一种差分隐私k-means 算法, 在计算聚类中心的过程中, 在求和函数和计数函数的查询结果中加入少量噪声来保证隐私, 但是该算法并未给出设置隐私预算ϵ的方式. 2006 年, Aggarwal 等人[3]提出先对原始数据集进行聚类操作, 用簇中心替换所有记录连同簇特征一起发布实现隐私保护的方法, 但这种处理方式使大多数数据遭到破坏, 降低了数据可用性. 2007 年, Nissim[4]提出PK-means 算法, 给出了如何计算误差下界和函数敏感度的方法, 使最终聚类模型满足差分隐私的要求. 2011 年, Dwork[5]分析了k-means 算法中敏感度的详细计算方法, 并给出了隐私预算ϵ的设置方式. 2013 年, 李杨等人[6]提出IDPk-means算法, 该算法经过一个对初始中心点的处理, 解决了经过差分隐私加噪后的初始中心点偏离过大导致聚类结果不可用的问题. 2016 年, 郑剑等[7]提出了一种针对线性回归的分析的差分隐私算法Diff-LR, 将线性回归模型的目标函数分解, 并将隐私预算分配为两部分对子函数进行扰动, 降低了算法的敏感度, 提升了模型精度. 2018 年, 杨庚等[8]提出一种面向差分隐私的隐私预算分配和数据发布方法, 利用泊松机制实现了差分隐私预算在数据发布中的应用, 可以达到隐私预算无穷分配的目的. 2019 年, 尚涛等[9]提出了一种等差隐私预算分配方法, 相比等比隐私预算分配, 该方法在保证了模型可用性的同时提升了精度, 但等差分配的方式不能实现隐私预算的任意分配, 只能应用于迭代次数固定或已知的模型训练中.
2012 年, Lee 和Clifton[10]认为差分隐私不关注攻击者背景知识, 只关注个体对数据库输出影响, 这不符合隐私相关的法律定义, 因此提出差分可辨性的概念, 它提供与差分隐私相当的隐私保护能力, 旨在限制个体被重新识别的概率, 隐私参数的设置也为从业者提供了一个简单的参数化方法. 2014 年, 欧洋伶[11]提出新的隐私保护算法Margin-Jump, 为非交互型数据列联表提供ρ-差分可辨性隐私保护. 通过随机替换数据集的敏感属性值, 以ρ-差分可辨性作为隐私保护模型. 目前, 对基于差分可辨性的聚类算法研究仍有较大空白.
2020 年, Shang 等人[12]研究了差分可辨性的指数机制应用于非数值型数据, 并通过数学证明得出差分可辨性的组合性质, 基于组合性质在聚类算法的迭代过程中添加噪声, 在MapReduce 框架上进行聚类,最终得到满足ρ-差分可辨性的聚类模型. 但是, 文献[12] 的方法中添加噪声的方式基于差分可辨性与差分隐私的映射关系, 即将差分隐私的隐私参数设置为ρ的函数, 并沿用了每轮隐私预算为上一轮一半的分配方式, 这并未很好地利用差分可辨性的性质, 本质上仍是差分隐私噪声. 因此, 本文提出基于差分可辨性组合性质推出的隐私参数分配方法, 可以满足隐私参数在迭代轮数固定情况下的平均分配和迭代轮数不固定时的任意分配, 并且最终得到的模型仍满足ρ-差分可辨性的要求.
本文结构如下. 第2 节介绍了差分可辨性的相关定义及组合性质. 第3 节给出了差分可辨性参数分配方法在聚类中的应用. 第4 节是实验分析, 验证本文方法的可行性. 最后, 第5 节总结全文, 并讨论未来可能的研究方向.
2 相关知识
Lee 和Clifon[10]认为,ϵ-差分隐私的定义存在一定缺陷: 隐私预算ϵ是评估安全性的指标, 它旨在限制邻近数据集输出结果的差异, 很难将其直接与个体可识别的概念联系在一起. 它不符合人们对于隐私安全的理解和相关法律对隐私的定义. 因此, Lee 和Clifton 提出ρ-差分可辨性的概念,ρ-差分可辨性也可提供强大的隐私保证, 其隐私参数ρ限制的是重新识别某个个体属于原始数据集的概率, 这与人们对隐私保护的法律意义相符.ρ-差分可辨性假设攻击者拥有背景知识L=
定义1 (ρ-差分可辨性) 给定一个查询函数f, 随机机制M是满足ρ-差分可辨性的, 当且仅当∀D′=D −vi, 且vi ∈U −D′, 有


则Δf为查询函数f的全局敏感度.
给定查询函数f的敏感度, 可借助拉普拉斯机制实现ρ-差分可辨性.

文献[12] 证明了差分可辨性和差分隐私具有类似的组合性质, 借助这些组合性质, 可以在聚类算法中实现差分可辨性.

推论2 (并行组合性) 假设有n个机制M1,M2,··· ,Mn, 机制Mi(i ∈[1,n]) 提供ρi-差分可辨性,Di是输入数据集D中互不相交的子集, 机制序列Mi(Di) 提供(minρi)- 差分可辨性.

并行组合性说明了,如果有n个随机机制M1,M2,··· ,Mn,他们均满足差分可辨性,其中机制Mi(i ∈[1,n]) 提供ρi-差分可辨性. 对一个数据集D进行划分后得到n个互不相交的子集D1,D2,··· ,Dn, 机制Mi对某一子集Di作用, 最终得到的模型序列(M1(D1),M2(D2),···Mn(Dn)) 满足(minρi)- 差分可辨性.
3 差分可辨性隐私参数分配方法

3.1 迭代轮数不固定时的隐私参数分配

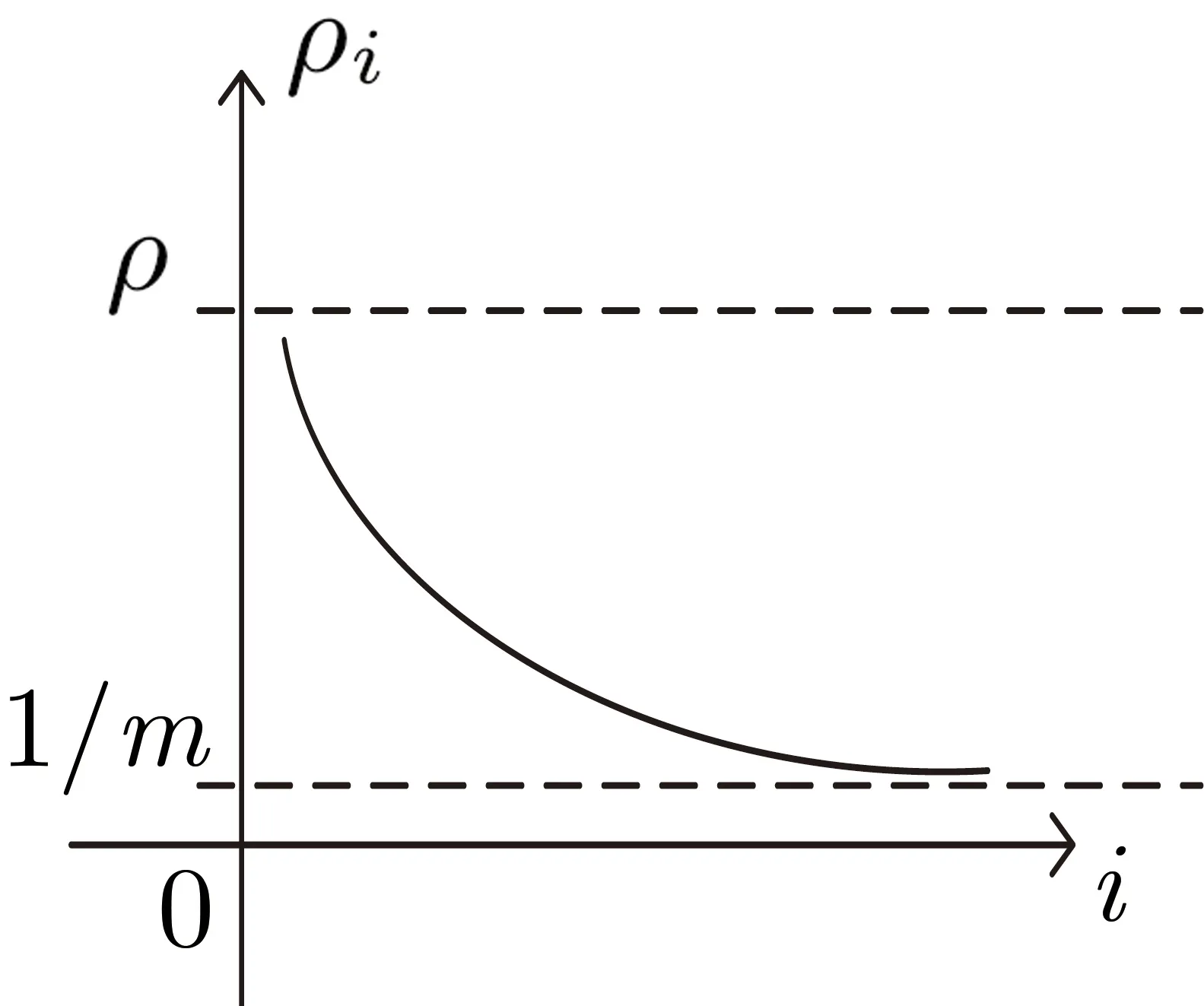
图1 DI 参数变化趋势Figure 1 Variation trend of parameter DI

指数部分收敛于1, 所以整个式子收敛于ρ.
该分配方法适用于任意轮数的迭代分配中, 随着迭代轮数越多, 最终模型满足的隐私保护能力越接近预设的ρ, 因此这是一种能够实现隐私参数无穷分配的方法. 但是迭代轮数较少时, 可能会浪费较多的隐私参数预算.
3.2 迭代轮数固定时的隐私参数分配
对于迭代轮数固定的聚类算法, 假设迭代轮数为N, 是一个固定值; 希望模型满足的隐私参数为ρ, 根据推论1 的序列组合性, 取每轮分配的隐私参数相等, 可得每轮迭代满足的隐私参数为


3.3 差分可辨性k-means 算法
为验证本方法的可行性, 本节给出结合差分可辨性的k-means 算法, 具体算法如下. 输入:d维空间[0,1]d的n个数据点p1,p2,··· ,pn, 分类个数k, 差分可辨性隐私参数ρ, 迭代轮数阈值N(可选);
输出:k个聚类中心点c1,c2,··· ,ck.

上述过程第5) 到7) 步循环执行, 直到簇的划分不再变化, 或迭代次数达到某一阈值停止.
根据差分可辨性的序列组合性, 每轮迭代运算满足差分可辨性, 那么迭代完成后的整体模型仍满足差分可辨性. 对于加入隐私保护的聚类算法, 由于隐私参数ρ在迭代过程中的递减, 添加的拉普拉斯噪声会逐渐增大, 导致聚类中心点偏移较大, 从而使迭代进入死循环或使最终的聚类结果丧失可用性. 文献[1] 中提出的差分隐私预算分配方法也有类似的特性. 解决办法是对迭代轮数设置一个较小的阈值, 才能保证较好的可用性.
4 实验分析
采用大数据集和小数据集两组数据集进行聚类测试. 小数据集是来自KEEL 的banana 数据集, 通过两种属性将5300 组数据划分为两个类别, 用于生成可视化的聚类结果查看分类的性能. 大数据集实验所用数据集来自UCI 机器学习库中的magic gamma telescope, 共19 020 条数据, 11 个特征, 用于对第3 节中的隐私参数分配方法进行验证实验, 同时与表1 中提到的方法进行性能对比. 实验环境为Windows 7 64 bit 操作系统, 开发语言为Python 3.7. 评价聚类性能好坏的指标为F-measure.F-measure 由常用于评价数据挖掘结果的指标准确率P(Precision) 和召回率R(Recall) 组成, 其计算值可用于评价聚类结果的效用. 准确率P和召回率R是主要参数,F-measure 大小与算法聚类结果和准确聚类结果的相似性成正比,F-measure 越大, 表明两个聚类结果的相似性越高, 最大值为1.F-measure 可通过下列公式计算.

表1 不同隐私参数分配方法Table 1 Different privacy parameter allocation methods

Pi和Ri(1≤k) 是第i个聚类的准确率和召回率, 聚类个数为k.Ci和Di分别表示数据集C和D的第i个聚类,|Ci| 和|Di| 为聚类Ci和Di中数据记录数目, coveri是聚类Ci和Di中相同数据记录数目, 计算各个聚类的F-measure 值Fi, 由各个聚类的Fi值加权平均得到指标F.
4.1 对小数据集的聚类实验
4.1.1 未进行加噪处理的k-means 聚类
实验设置k=2. 首先进行不加噪声处理的k-means 聚类, 结果如图2 所示.

图2 未经加噪处理的k-means 聚类结果Figure 2 k-means cluster without noise
通过两种不同的颜色区分两种不同类别(某种颜色并不代表特定的类, 仅作类的区分使用). 两个聚类中标出的点为聚类迭代过程最终产生的类中心点. 实验最终聚类模型的F-measure 值计算为48%.
4.1.2 差分隐私k-means 聚类实验结果
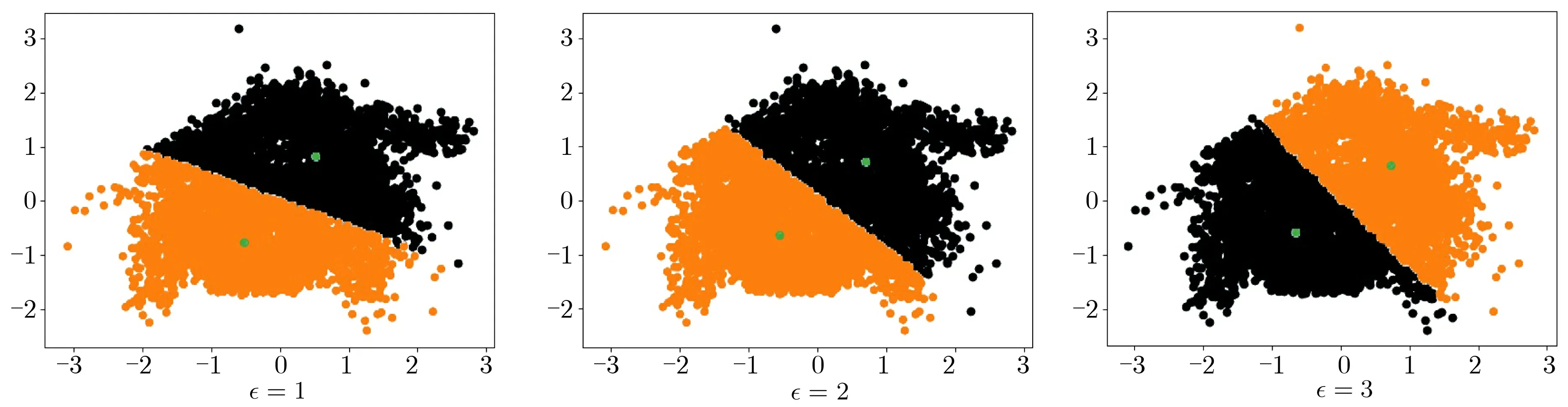
图3 差分隐私k-means 聚类结果Figure 3 k-means cluster with noise DP

图4 差分可辨性k-means 聚类结果Figure 4 k-means cluster with noise DI
根据第3 节中给出的隐私参数分配方法, 以ρ= 0.1 为例, 每轮隐私参数ρi= 0.003 16,0.000 56,0.000 24,0.000 15,0.000 12. 根据推论1, 最终模型满足0.080 58-差分可辨性, 显然也满足0.1-差分可辨性,但因迭代轮数较少而产生了隐私参数预算的浪费.
实验结果表明, 隐私参数ρ越小, 模型失真程度越高, 这与理论期待的情况吻合. 当设置合适的ρ值时, 聚类模型仍满足一定的可用性.
4.2 对大数据集进行k-means 聚类实验
数据集较小时, 对聚类过程中的参数进行处理可能无法很好体现出对聚类结果的影响, 因此本节对较大的数据集进行聚类测试. 使用表1 中列出的几种隐私参数分配方法, 对数据集进行k-means 聚类, 设置k=11, 此后分别添加差分隐私噪声和差分可辨性噪声并计算F-measure. 实验结果如图5 和图6 所示.

图5 大数据集差分隐私k-means 聚类结果Figure 5 k-means cluster of big dataset with noise DP
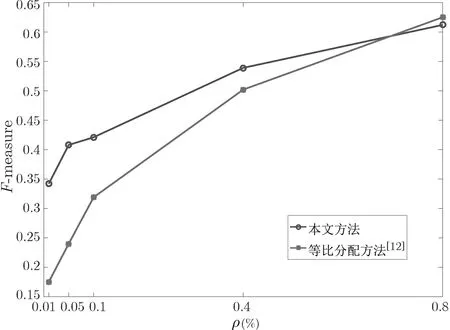
图6 大数据集差分可辨性k-means 聚类结果Figure 6 k-means cluster of big dataset with noise DI
实验结果显示, 随着隐私参数的增大, 差分隐私和差分可辨性方法表现出类似的性质,F-measure 值都出现了上升, 这与理论设想情况吻合. 差分可辨性方案分类表现最佳的对应F-measure 约为0.6, 略低于差分隐私方案的0.7, 一定程度上保持聚类的可用性.
如图6 所示, 在与文献[12] 的方法对比中, 使用本文方法进行的k-means 聚类性能明显较高.
4.3 迭代轮数对模型性能的影响
由于隐私参数在迭代过程中的逐轮递减, 迭代的同时添加的噪声也将逐步增大. 因此若不对迭代轮数进行限制, 到迭代后期对模型添加的噪声将非常大, 从而对聚类性能产生影响. 本小节将通过设置不同k-means 模型构建的迭代轮数, 观察模型性能变化, 讨论迭代轮数对模型性能的影响. 在本节实验中, 设置差分可辨性隐私参数ρ=0.8, 实验结果如图7 所示.

图7 迭代阈值对模型性能的影响Figure 7 Effect of iteration round threshold on model performance
根据实验结果, 当迭代轮数设置一个较小的阈值(5 轮左右) 时, 聚类性能可以得到保证,F-measure值在0.6 附近. 当迭代轮数增多到15 之后,F-measure 值下降到0.3 以下, 模型基本丧失可用性.
5 总结
本文针对传统的大数据聚类迭代算法, 基于组合性质提出了一种差分可辨性隐私参数的迭代分配方法, 满足了迭代轮数不固定情形下隐私参数的无穷分配, 也满足了轮数固定时隐私参数的平均分配, 且最终迭代生成的模型满足差分可辨性, 较好地体现了差分可辨性定义的先进性. 实验结果表明, 差分可辨性隐私参数分配方法适用于k-means 聚类算法, 通过与差分隐私k-means 模型的对比, 可以看出本方法处理后的聚类模型也具有较好的分类效果.
差分可辨性能提供与差分隐私等价的隐私保护能力, 它在隐私保护应用上同样有很大价值. 相较于已有长足发展的差分隐私保护理论, 差分可辨性的研究目前仍有较大的空白和广泛的前景.
目前对隐私参数ρ,m的选取大多依靠人为分析或实验来决定, 下一步仍需继续研究具有科学性的方法, 针对不同维度、不同规模的数据集制定合理的隐私参数. 除了聚类中的迭代加噪, 针对数据发布和其他机器学习等数据挖掘方法均有借助差分可辨性参数化隐私保护的研究前景, 可以探索差分可辨性的更多应用.
