改进的MIBS-64 算法积分分析研究*

李艳俊, 孙启龙, 欧海文, 汪 振

1. 北京电子科技学院, 北京100070

2. 密码科学技术国家重点实验室, 北京100878

1 引言

近年来, 为满足RFID (radio frequency identification)、智能卡、无线传感器等资源受限环境下的安全需求, 轻量级密码随之诞生, 而后倍受关注. 许多密码学者提出一系列轻量分组密码算法, 如PRESENT[1]、LED[2]、LBlock[3]、PRINT-cipher[4]、KLEIN[5]和SIMON[6]等.

MIBS[7]是一个轻量级分组密码算法, 由Izadi M 等人在CANS 2009 会议上提出. 针对MIBS 分组密码算法的现有分析结果包括线性分析[8]、积分分析[9]、差分分析[8]和不可能差分分析[10]等. 目前对于MIBS-64 最好的分析结果是14 轮差分分析[8], 数据复杂度为240个选择明文, 数据复杂度为237.2, 成功概率为50.15%; 对于MIBS-80 最好的分析结果是18 轮线性分析[8], 数据复杂度为260.98个已知明文,时间复杂度为276.13, 成功概率为72.14%. 虽然差分分析和线性分析的轮数较高, 但是成功率相对积分分析偏低.

积分分析是由Square 攻击发展而来的, Square 攻击[11]是对AES 最有效的攻击之一. 近年来, 积分分析广泛发展,已经应用于很多密码算法,如Rijndael[12]、ARIA[13]、Serpent[14]、AES[15]、Simeck[16]、TWINE[17]、Camellia[18,19]等. 2016 年, 随着可分性自动化搜索工具的逐渐成熟[20,21], 积分分析又一次占据了分析方法的主导位置. 于晓丽等人都对MIBS 算法进行了10 轮积分分析[9,22]. 本文基于MIBS-64 算法的密钥编排特点, 给出一类5 轮积分区分器, 并前向和向后分别扩展3 轮, 首次对MIBS-64 算法进行了11 轮的积分攻击, 攻击数据复杂度为258, 时间复杂度为259.75次11 轮加密, 攻击成功概率为100%.

2 预备知识

2.1 MIBS 算法简介

MIBS 算法整体结构使用传统的Feistel 结构[1], 轮函数采用SPN 结构, 其分组长度为64 比特, 支持64 和80 比特的密钥长度, 分别记为MIBS-64 和MIBS-80, 迭代轮数为32 轮. MIBS 中所有迭代操作都是基于半字节的, 也就是一个字有4 比特. 轮函数包括异或子密钥,S盒(4×4 比特) 层和一个线性层P(分支数为5), 此处线性层是设计文档中线性混淆和半字节置换的复合. MIBS 加密结构及轮函数结构见图1 及图2.

图1 MIBS 算法一轮加密结构Figure 1 One round structure of MIBS

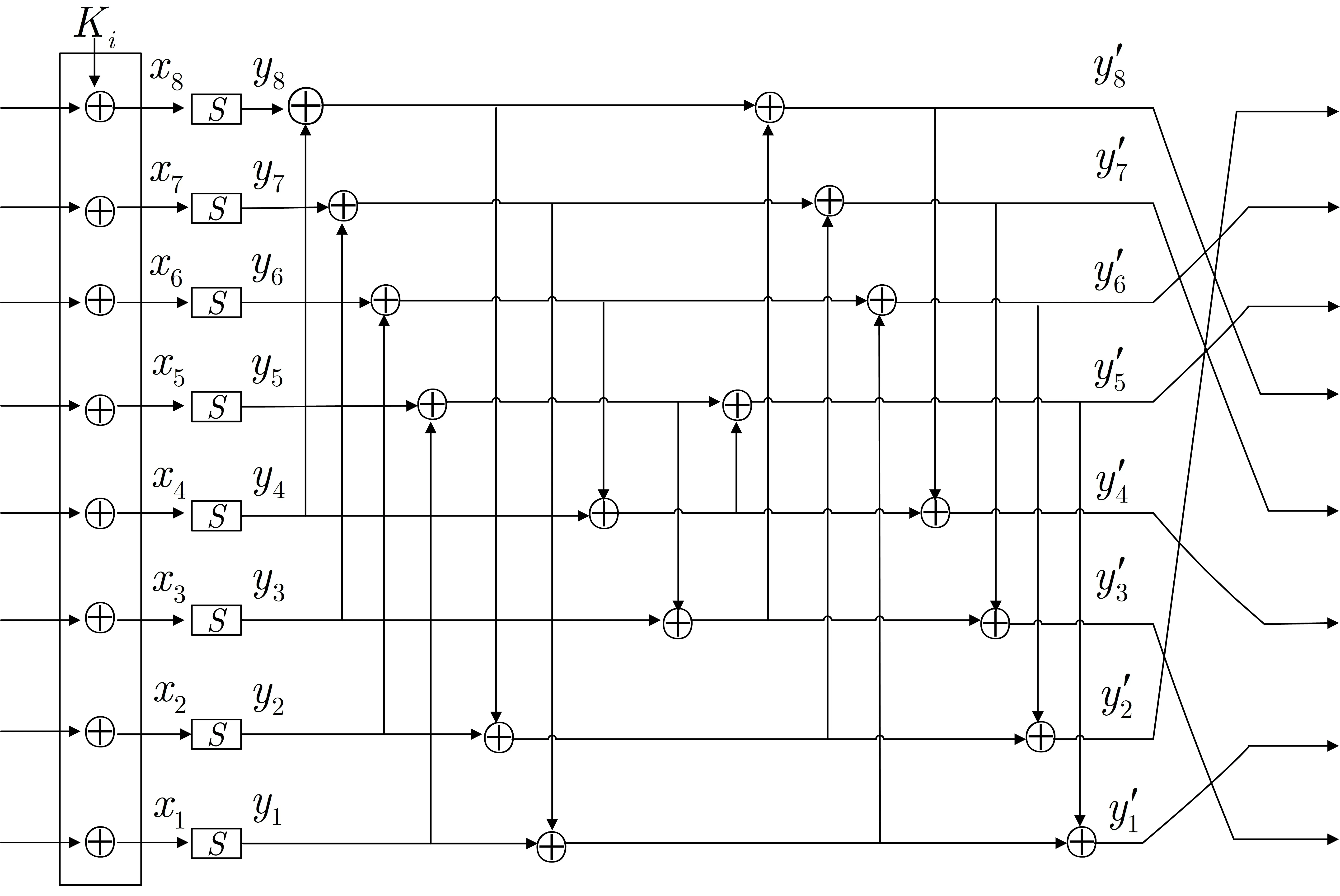
图2 MIBS 算法轮函数结构Figure 2 Round function of MIBS

MIBS 的密钥编排采用了与PRESENT 的密钥编排相同的设计原则. MIBS-64 密钥编排中, 通过64比特主密钥K: (k63,k62,··· ,k0) 生成轮密钥Ki, 其中0≤i ≤31. 若将密钥编排算法中第i轮的密钥状态表示statei, 则密钥编排算法的轮函数可以表示成如下的形式:

其中, ≫表示循环右移操作, [i～j] 表示此项操作是针对第i至第j比特变量,|| 表示连接操作, 轮函数中使用的S盒与F函数中使用的S盒相同. 最终, 第i轮状态statei的左侧32 比特将作为第i轮轮密钥Ki.

2.2 本文所使用的符号

现在我们介绍本文中使用的符号. 明文记为P= (X1,X0), 其中Xi= (xi,8,xi,7,··· ,xi,1),i=0,1,··· ,r −1, 本文中出现的其他符号含义如下:

3 MIBS-64 的密钥性质和积分区分器

MIBS-64 密钥编排算法中使用了循环移位、S盒查询、轮常数加等变换, 相邻两轮之间的32 比特密钥有17 比特重复或等价, 基于这个性质可以对MIBS-64 进行多轮攻击. 本节首先介绍MIBS-64 的密钥性质, 然后提出MIBS 算法的一类5 轮积分区分器.

3.1 MIBS-64 的密钥性质

根据MIBS-64 密钥编排算法, 第1 轮至第11 轮之间的密钥存在部分重复和等价关系, 本文主要使用下述密钥编排性质.

本文根据我院医疗设备管理的现状和要求，设计出一套适合医院自身管理流程的医疗设备全生命周期管理系统，有效地提高了医院的工作效率和经济效益。该系统基本涵盖了医疗设备管理的全过程，满足我院医学工程科对医疗设备管理的实际需求，提高了我院医疗设备信息化管理的整体水平。

3.2 一类5 轮积分区分器

基于轮密钥之间的关系, 选取合适的5 轮积分区分器, 向前解密3 轮, 向后加密3 轮, 可以攻击11 轮MIBS-64. 这类5 轮积分区分器需要具备以下特点:

(1) 选择X0= (C,C,x0,6,x0,5,x0,4,x0,3,x0,2,x0,1), 其中x0,1～x0,6任意两个活跃, 为不增加猜测多余密钥的计算量x0,7～x0,8被设置为常量.

图3 轮密钥之间的关系Figure 3 Relationship between round keys

(2) 5 轮积分区分器输出X6经过S盒后得到Y6= (y6,8,y6,7,y6,6,y6,5,y6,4,y6,3,u,u), 其中y6,8～y6,3共6 个半字节可能为平衡半字节, 为不增加猜测多余密钥的计算量y6,2～y6,1被设置为未知的半字节u. 若存在i个半字节的每个值出现偶数次, 则猜测密钥中错误密钥通过的的概率小于2−12.68i[9,19].

根据上述特点, 通过搜索得表1 中13 个5 轮积分区分器.

下述引理2 将证明表1 中区分器1 的正确性, 引理3 将证明表1 中区分器5 中y6,3半字节平衡的正确性, 其余平衡半字节的证明方法相似, 从略. 根据密钥编排特点, 为降低猜测多余密钥的计算量, 上述区分器中的平衡字节y6,2和y6,1并不会被使用.

表1 MIBS-64 算法5 轮积分区分器Table 1 5 rounds integral distinguishers of MIBS-64

引理2 如果选择明文结构为(X1,X0) = (CCCCCCCC,CCCCCCA2A1), 也就是x0,2,x0,1是活跃的半字节, (X1,X0) 的其余半字节都为常数, 记t1=P−1(X7)7⊕y6,7,t2=P−1(X7)8⊕y6,8, 则每个ti的值都会出现偶数次.

证明: 如图4 所示, 根据Feistel 结构特点, 得到X7=X1⊕Z2⊕Z4⊕Z6, 在选择明文攻击中, 明文(X1,X0) 和密文(X7,X6) 已知, 故有:

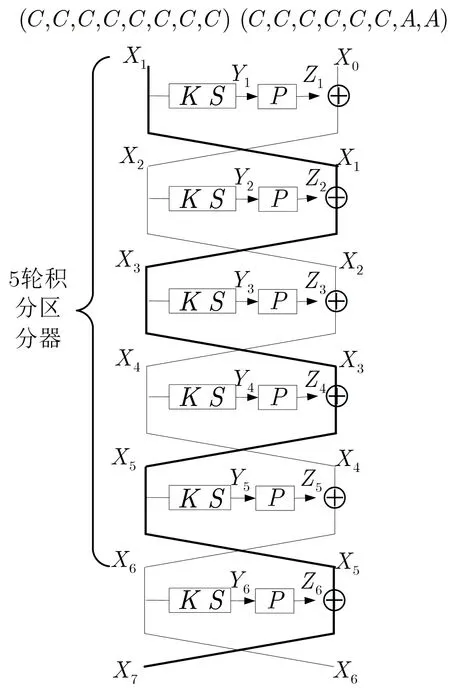
图4 MIBS 算法5 轮积分区分器Figure 4 5 round integral distinguisher of MIBS

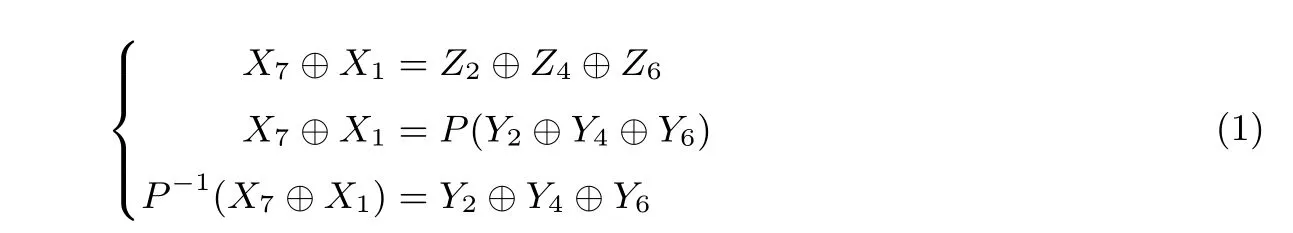
根据方程(1)我们知道P−1(X7⊕X1)=Y2⊕Y4⊕Y6, 故P−1(X7)i ⊕P−1(X1)i=y2,i ⊕y4,i ⊕y6,i

所以t1=P−1(X7)7⊕y6,7=P−1(X1)7⊕y2,7⊕y4,7, 其中y2,7=S(x2,7⊕k2,7),x2,7=x0,7⊕z1,7,而x0,7,x1,7是常数, 故x2,7是常数, 由于P−1(x1)7也是常数, 故此t1的取值规律与y4,7的取值规律是相同的, 下面分析y4,7的取值规律:

考虑x4,7得:

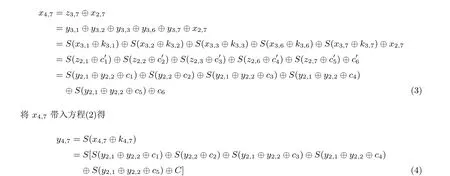
令y=y2,1⊕y2,2, 对于y的每一个值,y2,2都是活跃的, 所以y4,7的每个值都出现16 次, 即满足y4,7的每个值都出现偶数次.

同理, 可证t2的每个值也出现偶数次.

引理3 如果选择明文结构为(X1,X0) = (CCCCCCCC,CCCA5A4CCC), 也就是x0,5,x0,4是活跃的半字节, (X1,X0) 的其余半字节都为常数, 记t3=P−1(X7)3⊕y6,3, 则t3的每个值出现偶数次.

证明: 前部推导过程与引理2 证明相似, 可得t3的取值规律与y4,3的取值规律是相同的, 下面分析y4,3的取值规律:

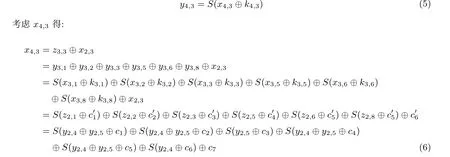
将x4,3带入方程(5)得

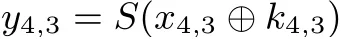
与引理2 证明不同, 此处y4,3的表达式中同时出现了S(y2,5⊕c3) 和S(y2,4⊕c6). 令y=y2,4⊕y2,5, 则对于y的每一个值,y2,5是活跃的. 又

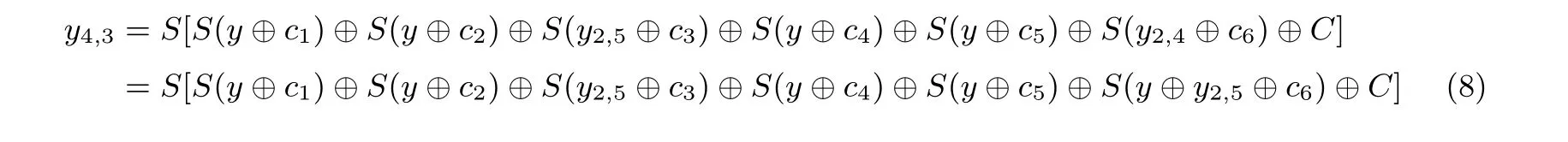
所以S(y2,5⊕c3)⊕S(y ⊕y2,5⊕c6) 的每个值出现偶数次, 因此结论成立.

4 MIBS 的11 轮积分攻击

4.1 积分区分器选取

在针对11 轮的MIBS 攻击中使用第3.2 节表1 中的5 轮积分区分器, 因为需要用t值过滤错误密钥,t值的比特数越多, 错误密钥被过滤掉的概率越大. 因此根据密钥性质和5 轮区分器的平衡比特数量, 选用第8 个区分器进行下述恢复密钥攻击. 选择x3,5,x3,2活跃, 具体过程如图5 所示.

图5 MIBS 算法11 轮攻击Figure 5 Attack on 11 rounds MIBS

第4 轮至第8 轮为区分器, 输入表示成(X4,X3), 满足:

x3,5,x3,2活跃, 则y7,[8,7,6,4,3]每个值出现偶数次, 表达式为:

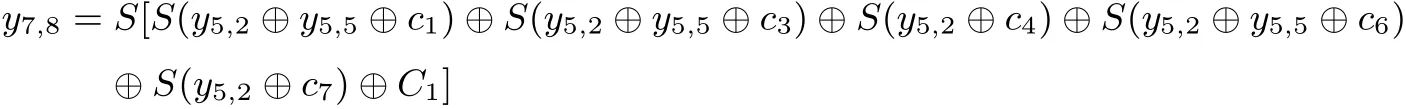
与引理类似, 有:

由此, 对于上述t1～t5每个值都出现偶数次, 即这5 个半字节位置t1||t2||t3||t4||t5的每个值出现偶数次. 对于随机置换, 根据文献[9] 和[19], 这20 个比特位置的值出现偶数次的概率小于2−12.68×5=2−63.40.

4.2 攻击步骤

Step.1 定义如下由28个64 比特构成的一个结构, 可以表示成(X3,X2) 的形式, 并满足:

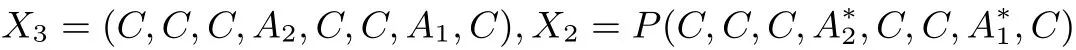
4.3 复杂度分析

在11 轮恢复密钥攻击中, 共猜测主密钥第63～32、21～0 共54 比特, 随机密钥通过5 轮积分区分器的概率为2−63.40,即只有1 个正确的54 比特密钥被保留. Step.1—2 需要计算250×28×2.25÷11≈255.75次11 轮加密. Step.3 需要计算258次11 轮加密. Step.4 需要计算250×28×24×2.3÷11≈259.75次11 轮加密. Step.5 得到254×2−63.40+1≈1 个54 比特密钥, 猜测剩余的10 比特密钥, 只需要进行210次11 轮解密.

因此, 上述攻击的整体时间复杂度由Step.4 决定, 共需时间复杂度259.75次11 轮加密, 数据复杂度为258.

5 结束语

本文对分组密码算法MIBS-64 进行了积分分析, 基于密钥编排算法构建一类5 轮积分区分器, 向前加3 轮, 向后加3 轮, 11 轮的密钥恢复攻击数据复杂度为258, 时间复杂度为259.75. 与差分分析、线性分析、截断差分分析等方法相比, 虽然密钥恢复的轮数较少, 但是这种攻击方法成功的概率为100%, 在算法实际攻击中具有重要意义. 本攻击结果适用于MIBS-64, 类似地可以推广至MIBS-80. 由此可见, 轮密钥之间的关系对算法安全性有重要影响, 若能考虑这些关系对S盒的作用, 将会改进现有分析效果, 这也是我们下一步的工作.