基于深度学习的多面体差分攻击及其应用*

付超辉, 段 明,2, 魏 强, 吴茜琼, 周 睿,2, 宿恒川,2

1. 信息工程大学 网络空间安全学院, 郑州450001

2. 河南省网络密码技术重点实验室, 郑州450001

1 引言

自AlphaGo 诞生以来, 深度学习迅猛发展, 已广泛应用于社会生活的各个领域, 如智能机器人、智能医疗、智能安防、智能家居、智能交通、智慧城市以及计算机视觉、语音和图像识别、机器翻译、自动驾驶、信息推荐等.

2019 年美密会上, Gohr[1]提出深度学习用于密码算法分析的技术, 并对Speck 算法进行了差分攻击, 对减少数据复杂度有很好的效果. 本文结合多面体差分的思想[2–4], 利用深度学习的方法创新提出了多面体差分神经网络区分器. 该区分器由一个残差神经网络构成, 可以对特定输入差分对应的输出密文分布特征进行学习. 残差网络训练完成后, 可对密文进行预测, 根据预测值即可判断该密文是否是由特定输入差分产生. 该多面体差分神经网络区分器相对于Gohr 提出的单差分区分器精度更高, 一定条件下, 利用其进行密钥恢复的成功率也有一定提升, 为我们提供了一种在密钥恢复成功率和数据复杂度时间复杂度之间折中的方法.

Simeck 算法是Yang[5]等在CHES 2015 上提出的一种轻量级的分组密码, 结合了NSA 在2015 年设计的Speck 和Simon[6]算法的特征, 从轮函数上看更像Simon 算法, 从密钥扩展上看更像Speck 算法. 该算法能够满足RFID 设备低功耗高性能的需求, 且适用于IOT 设备的安全[7], 可在16 位处理器上高效执行[8]. 自提出以来, 出现了大量的针对该算法的攻击分析, 如差分攻击[9]、线性攻击[10]、不可能差分攻击[5]、积分攻击[11]、相关序列攻击[12]、零相关线性分析[13]等, 虽然针对该算法的攻击方法很多,但大多都是理论攻击, 针对13 轮的Simeck32/64 攻击, Bagheri[10]给出了实际攻击结果, 但数据复杂度和时间复杂度较高.

我们利用多面体神经网络区分器、单差分神经网络区分器及两种区分器的混合对13 轮Simeck32/64算法进行了密钥恢复攻击, 相对于现有针对该算法的攻击它们都降低了所需数据复杂度和时间复杂度,表1 给出了利用两种区分器的混合进行密钥恢复的结果, 数据复杂度和时间复杂度分别为217.7和232.7,与已有的攻击结果相比, 复杂度分别减少为原来的1/212和1/23, 同时我们也给出了利用单差分神经网络区分器攻击的结果, 结果显示在略微降低密钥恢复成功率的情况下, 所需数据复杂度和时间复杂度还可以再次降低. 其中文献[10] 中给出的是恢复1 比特密钥的时间复杂度, 此处对其进行了换算.

表1 Simeck32/64 算法Table 1 Simeck32/64 algrithm

2 基础知识

2.1 Simeck 算法

Simeck 是一种轻量级分组密码, 由Yang[5]等在CHES 2015 提出, 采用Feistel 结构, 记为Simeck2n/mn,其中分组大小为2n(n=16,24,32),mn表示密钥大小. 本文主要研究Simeck32/64,即分组大小为32 比特、密钥大小为64 比特. 轮函数可表示为L(i+1)=((Li≪5)&Li)⊕(Li≪1)⊕Ri⊕Ki,

其单轮函数迭代结构如图1 所示.

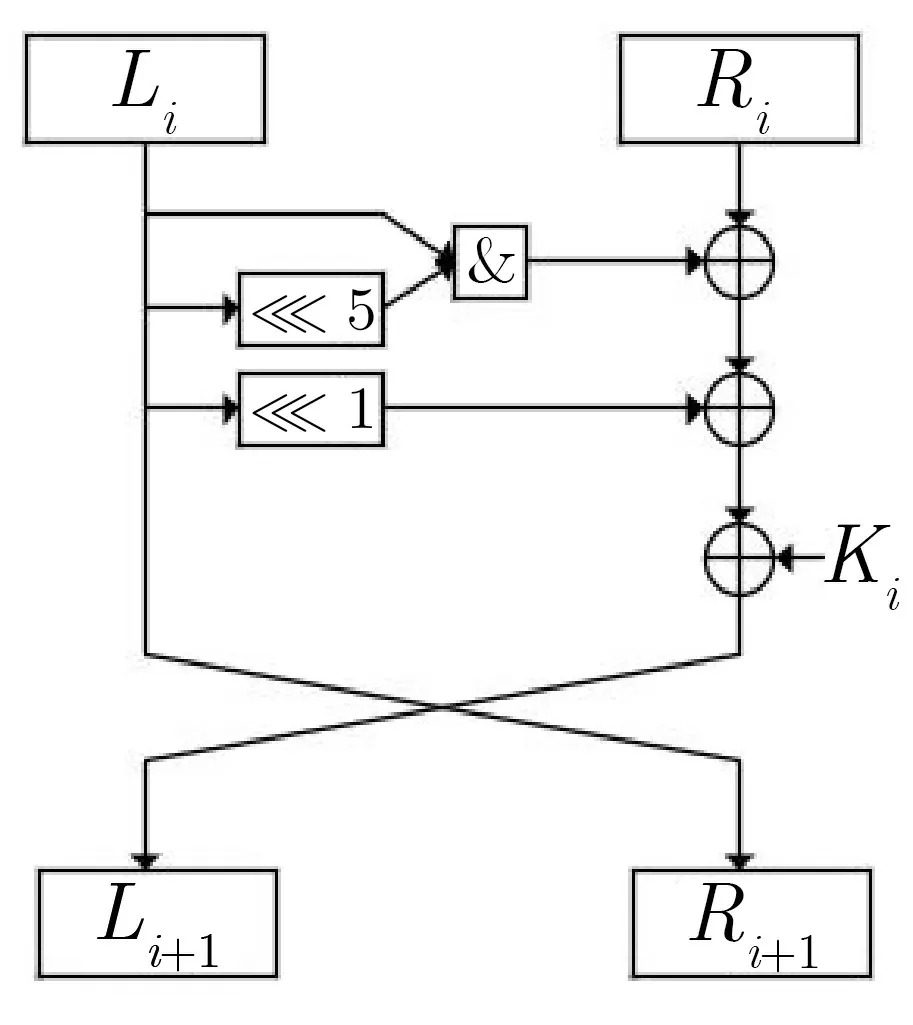
图1 Simeck 算法轮函数迭代结构Figure 1 Architecture of Simeck

2.2 差分分析

假设F是一个映射,F: (0,1)n →(0,1)m, 一个差分转移是指一对(△in,△out)∈(0,1)n×(0,1)m,其映射F:(0,1)n →(0,1)m的概率称为差分转移概率, 记作

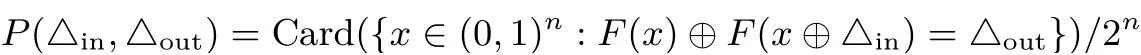
对于一个简单的迭代结构的分组密码, 差分特征是指一个差分转移序列△0,△1,···,△n. 差分区分器是一个高概率的差分特征. 当给定具有某种差分的明文数据时, 密文输出具有非随机特性, 差分攻击就是利用这种特性的一种密码算法分析方法.

当给定输入差分△和加密轮数r, 综合使用多个输出差分特征时, 我们用

2.3 多面体差分分析

传统的差分密码分析利用两个明文在加密时的统计相关性, 当我们对两个文本在状态空间中的绝对位置不感兴趣时, 两个明文之间的差异完全决定了它们的相对位置. 当有多个明文时, 选择其中一个明文作为参照点, 就只需考虑它们相对于参考明文的差值, 据此Tiessen 在2016 年提出了多面体差分思想, 并在多个密码分析中得到应用[2–4].

例如有d+1 个明文, 可以用d差分的元组来描述它们的相对位置. 通常我们称(m0,m1,···,md) 为(d+1) 面体, 相应的差分(m0⊕m1,m0⊕m2,···,m0⊕md) 为d差分,m0称为锚定值. 因此, 如果给定一个d差分和锚定值, 我们就可以唯一地确定其相应的(d+1) 面体.

多面体密码分析考虑了明文集在加密时的相互依赖性, 是标准差分密码分析方法的一个扩展, 是一个通用的方法, 可以包含更高阶的差分. 在实际密码分析中具有一定的实用价值, 可以为我们在时间和数据复杂度之间提供一种折中.

2.4 神经网络差分区分器

神经网络差分区分器最早由Gohr[1]提出, 由一个残差神经网络构成. 残差神经网络是深度学习的模型之一. 利用该网络, 对给定输入差分的某算法的输出差分分布特征进行学习, 并利用训练的网络对给定的密文进行预测, 看该密文是否符合其输出差分分布. 区分器进行预测时, 利用了输出差分的分布特征, 这其中很多特征对于传统的纯差分区分器来说是不可见的, 并且该区分器在用于密钥恢复攻击时, 大大降低了所需数据复杂度和时间复杂度. 下文我们将该区分器简称为单差分神经网络区分器.

3 基于深度残差神经网络的多面体差分区分器

下文将基于深度残差神经网络的多面体差分区分器简称为多面体神经网络区分器. 我们从功能的角度对多面体神经网络区分器进行一个简要描述. 多面体神经网络区分器的功能类似差分区分器. 首先, 训练一个多面体神经网络区分器. 给定输入差分为△0,△1,···,△d用形如(P,P ⊕△0,P ⊕△1,···,P ⊕△d)的明文训练一个多面体神经网络区分器. 其次, 利用该区分器进行预测. 其输入为由上述明文产生的密文,输出为Z,Z ∈(0,1), 表示区分器对密文的预测值. 一般意义上当Z> 0.5 且越接近1 时, 说明该密文是由输入差分为△0,△1,···,△d的明文产生的. 假定多面体神经网络区分器的输入为n个密文, 密钥为k,第i个密文应的输出为Zki,Zki ∈(0,1) , 综合多面体神经网络区分器的多个输出, 可利用

来区分枚举密钥的好坏, 当V2值大于一临界值时, 说明该枚举密钥是一个好的密钥. 数据复杂度与n值相关.

当d= 2 时神经网络区分器为3 面体神经网络区分器, 当d= 3 时神经网络区分器为4 面体神经网络区分器, 当d=1 时神经网络区分器为2 面体神经网络区分器, 也是Gohr 提出的单差分神经网络区分器. 下文以3 面体神经网络区分器为例进行说明.

3.1 三面体神经网络结构

以3 面体神经网络区分器为例, 下面直接给出对应Simeck32/64 算法我们的最好模型及参数. 深度学习神经网络一般由数据预处理、输入层、隐藏层和输出层构成, 在数据预处理和输入层, 将一组具有特定输入差分的明文记作(P,P ⊕△0,P ⊕△1), 3 个元素共96 比特, 整体看作一个行向量作为网络的输入.隐藏层共十一层, 第一层的初始化使用一维卷积和正则化, 卷积使用32 个filter, 激活函数使用Sigmoid函数, kernel_size 设置为1. 隐藏层的其它层全部由一维卷积和正则化构成, kernel_size 设置为3, 其余参数与隐藏层第一层相同. 输出层由三层构成, 前两层各有96 个神经元, 每层后面都有正则化、矫正层,激活函数为ReLU 函数, 最后一层有一个神经元, 激活函数为Sigmoid.

3.2 三面体神经网络区分器的训练

训练数据和验证数据均用随机数生成. 三个明文分别记作P0,P1=P0⊕△0,P2=P0⊕△1,P3=(P0⊕Random1),P4=(P0⊕Random2). 此处△0=0x0000/0001,△1=0x0000/0004, Random1和Random2 均为32 比特随机数. 进行r轮Simeck32/64 算法训练时, 密钥由随机数生成, flag 也由随机数生成且flag 属于集合(0,1). flag=1 时, 神经网络的一组输入数据为(P0,P1,P2), flag=0 时神经网络的一组输入数据为(P0,P3,P4) . 训练的集合大小为107, 验证集合大小为106. 每次训练我们运行50 个epoch, 每个batch 大小为5000, 使用Keras 中默认参数的Adam 算法对均方误差损失和基于L2权重正则化(正则化参数c= 10−5) 惩罚进行优化, 采用循环学习效率调度. 利用GTX1650 显卡我们训练了一个8 轮和一个9 轮的3 面体神经网络区分器, 每个区分器训练50 个epoch, 一个epoch 大约需要5 分钟, 结果如图2 和图3 所示.

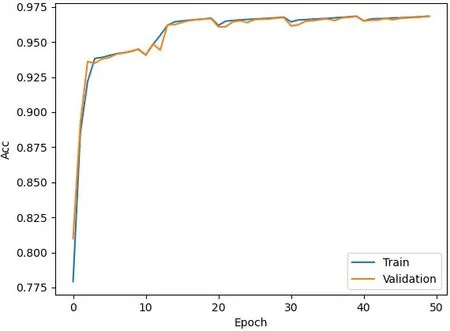
图2 N8 三面体神经网络区分器精度Figure 2 Accuracy of 8-round 3-polytopic differential neural network distinguisher

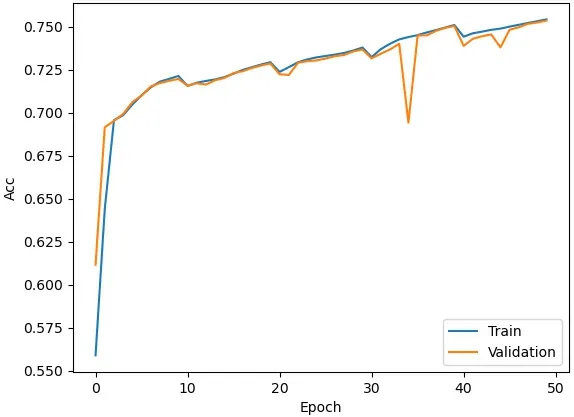
图3 N9 三面体神经网络区分器精度Figure 3 Accuracy of a 9-round single differential neural network distinguisher

其中,x轴表示训练的epoch,y轴表示精度, 蓝线表示训练精度, 橙线表示预测精度. 随着训练周期的增加, 神经网络区分器的精度基本稳定. 相似的, 我们利用输入差分△0= 0x0000/0001[9],△0=0x0000/0002, 或△0= 0x0000/0004 等训练了多个8 轮和9 轮的单差分神经网络区分器, 结果如表2 所示, N8 和N9 表示8 轮和9 轮神经网络区分器. 通过对比两种类型的神经网络区分器可以发现, 轮数相同的情况下多面体神经网络区分器的预测精度更高.

表2 单差分神经网络区分器和多面体神经网络区分器精度对比Table 2 Accuracy comparison between single differential neural network distinguisher and polytopic neural network distinguisher

4 多面体差分神经网络区分器的应用

在本节我们将利用 3 面体差分神经网络区分器 N9 和单差分神经网络区分器 N8 对 13 轮Simeck32/64 进行密钥恢复攻击, 并通过该实例对密钥恢复攻击过程和原理进行说明.

4.1 区分器扩展

这里主要对13 轮的Simeck32/64 进行最后一轮子密钥进行攻击. 攻击第13 轮时, 将9 轮的3 面体神经网络区分器扩展为11 轮的区分器, 添加一个两轮区分器, 其差分转移路径为

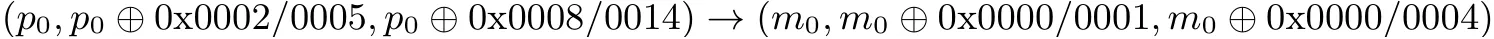
(0x0002/0005,0x0008/0014) 为输入3 面体的2 差分. 其中输出以约1/16× 1/16 = 1/256 概率为(m0,m0⊕0x0000/0001,m0⊕0x0000/0004) , (0x0000/0001,0x0000/0004) 为输出3 面体的2 差分. 该2 差分也是我们训练神经网络时输入数据的差分. 此处, 我们将这样的3 面体数据称为可用差分结构. 一般来说, 可用差分结构是一个d+1 多面体数据, 它的d差分与训练多面体神经网络区分器的d+1 面体数据的d差分相同. 之后将添加的两轮区分器的输入解密一轮, 结果即为选择明文, 以其作为13 轮加密的输入, 这样即可保证选择明文加密1 轮后, 输出3 面体的2 差分以概率1 为(0x0002/0005,0x0008/0014),加密3 轮后, 输出3 面体的2 差分以概率1/256 为(0x0000/0001,0x0000/0004), 即9 轮3 面体神经网络区分器的输入2 差分以概率1/256 为(0x0000/0001,0x0000/0004).

9 轮3 面体神经网络区分器经过2 轮扩展后, 其输入3 面体数据的2 差分以约1/256 的概率为(0x0000/0001,0x0000/0004), 为了扩大该概率, 减小数据复杂度, 我们利用了中性位[14]来构造明文结构.实际上我们在构造明文结构时, 利用了中性位比特变化但不改变输出差分的性质, 首先选定一个3 面体明文组, 然后对其6 个中性位比特进行变化, 从而扩展出64 个3 面体明文组, 称其为一个明文结构. 13 轮攻击采用的中性位比特为(0,1,2,3,4,6), 扩展后的64 个3 面体明文组经加密后可得到64 个3 面体.

4.2 密钥恢复过程

明文结构经过13 轮加密后得到相应密文结构, 猜测最后一轮子密钥, 并利用候选子密钥搜索策略给出候选密钥, 利用这些密钥解密该密文对组, 得到的结果作为输入进入3 面体神经网络区分器N9, 经区分器和公式(2)计算后得到一组V2值, 将该值和临界值Cut1比较, 如果大于Cut1, 就将解密最后一轮得到的密文结构用于猜测倒数第二轮子密钥. 其过程是, 利用猜测的倒数第二轮子密钥解密倒数第二轮数据, 得到的结果形如(m0,m1,m2), 取(m0,m1) 作为输入进入单差分神经网络区分器N8, 经区分器和公式(2)计算出该轮的V2值, 如果该V2值大于临界值Cut2, 那么用于解密的两轮子密钥即是所求.

简要地说该过程主要分为两个步骤: 第一步, 搜索最后一轮候选子密钥; 第二步, 在最后一轮子密钥确定后, 搜索倒数第二轮子密钥. 两个步骤都利用了输出密文的差分分布特征. 当然, 也可以只利用第一个步骤确定最后一轮子密钥, 增加第二步是为了更好地确认第一步搜索出的最后一轮子密钥的正确性. 第二步对于确定最后一轮子密钥起到了辅助作用.

4.2.1 候选子密钥搜索策略

最后两轮候选子密钥搜索均采用了贝叶斯优化方法[15]对密钥搜索策略进行了改进. 贝叶斯优化是一种在不知道函数方程的情况下, 根据已有的采样点求取函数最大值及其相应参数的方法. 该方法可快速找到函数最大值, 其包含两个核心过程: 一个是先验函数, 先验函数主要利用高斯过程回归, 其求解按贝叶斯推断进行; 一个是采集函数, 包括UCB (边探索边利用) 方法等, 目的是找到最佳样本集. 在我们的攻击模型中, 可把区分器看作一个黑盒函数, 寻找该黑盒函数的最大值过程即搜索候选子密钥过程, 首先猜测一个子密钥, 由该子密钥解密密文再经黑盒函数, 所得结果求均值方差, 再利用采样点值经贝叶斯推断即可得出候选子密钥. 采样点值可以利用区分器和样本集在错误密钥情况下预计算获得.

4.2.2 采样点值计算

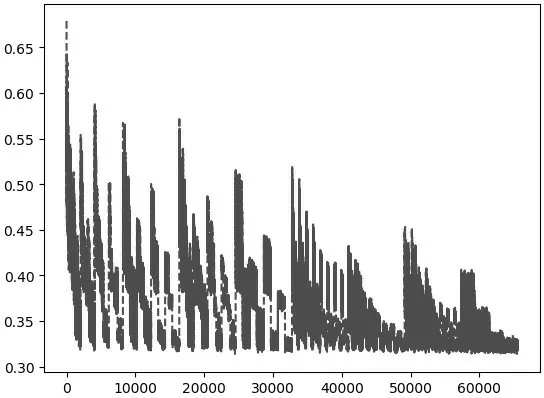
图4 三面体神经网络区分器N9 错误密钥均值分布Figure 4 Wrong key response profile of 9-round 3-polytopic differential neural network distinguisher

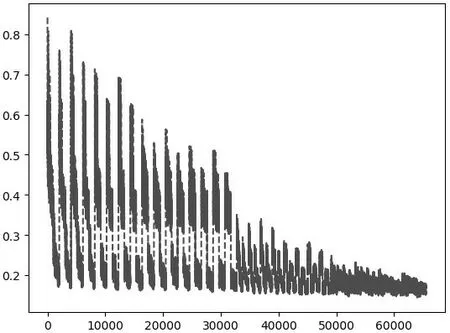
图5 单差分神经网络区分器N8 错误密钥均值分布Figure 5 Wrong key response profile of 8-round single differential neural network distinguisher

其中, 横轴表示密钥差△, 纵轴表示神经网络区分器输出均值. 该采样点值主要用在贝叶斯推断中.

4.2.3 候选子密钥搜索算法

由上述知识为基础, 候选密钥搜索算法可总结如算法1 所示. 其中,S为密钥集合,N为神经网络区分器,n为候选密钥个数,m为密文组个数, count 为贝叶斯优化算法迭代次数.

算法1 候选密钥搜索算法Input: S := {k0,k1,···,kn−1},N,n,m,count Output: S 1 for iter < count do 2 解密1 轮m 个密文对组得到密文组Pi,k, k ∈S;3 用神经网络区分器N 预测Pi,k 得到中间变量Zki;4 Zk i 为输入利用公式(2)得到中间变量wk;5 对每个密钥构建L = L‖[k,wk];6 对每个密钥求均值mk = ∑m i=0 Zki/n;7 构建中间变量λk = ∑n−1 i=0 (mk −µ△⊕k)2/σ2△⊕k,k ∈{0,1,···,216 −1};8 用S 记录λk 最小的n 个值对应的k 作为候选密钥;9 end

用L保存枚举的密钥和计算得出的wk, 其中保存密钥和wk的个数为n×count. 如果其中的某个wk超过了临界值Cut1, 那么我们将该算法扩展倒倒数第二轮, 如果该轮的wk超过了临界值Cut2, 那么我们的密钥搜索就结束了, 此时便得到了最后两轮的子密钥.

在密钥恢复攻击的过程中, 首先对所有的密文结构进行候选密钥搜索, 如果没有找到合适的密钥, 就继续主循环的迭代, 直到找出使得该轮wk> Cut1子密钥. 算法扩展到倒数第二轮, 密钥搜索过程相同,该轮利用的密文结构是由猜测的最后一轮子密钥解密原始密文数据得来. 在这些迭代过程中使用了UCB的方法.

在13 轮的攻击实验中我们分别使用了1024 个密文结构, 单个密文结构包含64 个3 面体明文对组, UCB 方法的参数为10, 贝叶斯密钥搜索迭代次数为2048, Cut1= 1.0, Cut2= 10.0, 候选密钥个数n=32×5=160.

4.3 攻击结果及复杂度估计

在13 轮密钥恢复攻击实验中, 对100 个密钥进行了恢复, 统计发现, 共用时17 984 秒, 恢复一个密钥平均用时180 秒, 最后1 轮子密钥完全正确的概率为98%, 倒数第二轮子密钥误差全部在2 比特以内.

数据复杂度为210×3×64=217.6, 以一次Simeck 运算为单位, 估计时间复杂度为(l1×1.5+l2)×22×22×217≈232.8, 其中217表示一次候选子密钥搜索所需时间复杂度, 两个22×22×217表示4次候选子密钥搜索和神经网络预测所需时间复杂度,l1≈1024 表示需进行最后一轮解密的数据结构个数,l2≈2095 表示在wk>Cut1的情况下, 进行倒数第二轮解密的密文结构个数.

4.4 其它轮子密钥的恢复

通过上述攻击过程, 我们可以发现该攻击方法的主要计算复杂度在于, 输入明文经3 轮加密后是以1/256 概率得到我们想要的输出密文即可用差分结构, 该输出密文再经神经网络区分器、候选密钥搜索等过程最终找到正确密钥. 在未知哪一个明文输入能得到可用差分结构时, 我们只能将所有的输入明文结构枚举. 但是, 在最后一轮子密钥搜索完成后, 就可以得到一个输入明文结构其对应的3 轮加密输出为可用差分结构, 以及一个完全正确的最后一轮子密钥. 利用此明文结构即可以常数时间恢复其它各轮子密钥,从而得到初始完整密钥.

5 密钥恢复效率对比分析

本节我们主要讨论多面体差分相对于单差分带来的精度提高, 在密钥恢复效率上的具体体现. 主要以3 面体神经网络区分器和单差分神经网络区分器的应用作对比. 同时也涉及到了3 面体神经网络区分器和单差分神经网络区分器的混合使用, 即密钥恢复攻击的第一步使用3 面体神经网络区分器, 第二步使用单差分神经网络区分器.

单差分神经网络区分器的训练已由第3 节给出, 下文我们将直接给出单差分神经网络区分器进行密钥恢复的结果. 另使用单差分神经网络区分器时, 该区分器由9 轮扩展为11 轮需添加的两轮差分特征为(0x0002/0005,0x0000/0001), 得到一个可用差分结构的概率约为1/16. 3 面体神经网络区分器由9 轮扩展为11 轮时, 得到一个可用差分结构的概率约为1/256. 本节表格中涉及到的概率即为得到可用差分结构的概率.

5.1 无概率攻击实验

在该实验中, 我们将2 差分为(0x0000/0001,0x0000/0x0004) 的3 面体神经网络区分器与单差分为0x0000/0002 的神经网络区分器进行对比. 密钥恢复攻击的轮数为10 轮. 多面体差分攻击的两个步骤使用3 面体神经网络区分器N9 和N8, 单差分攻击的两个步骤使用单差分神经网络区分器N9 和N8. 因轮数为10 轮, 故不需考虑由输入明文到可用差分结构的概率. 结果如表3 所示.

表3 无概率条件下单差分神经网络区分器和三面体神经网络区分器密钥恢复精度对比Table 3 Comparison of key recovery accuracy between single differential neural network distinguisher and polytopic differential neural network distinguisher without probability

通过该实验我们确认了高精度的3 面体神经网络区分器在密钥恢复攻击中, 效果要好于精度低的单差分神经网络区分器. 另外, 该结果也与采用UCB 方法时的主循环次数相关, 一般意义上主循环次数越大越高密钥恢复成功率越高, 但计算复杂度也越大, 此处主循环次数为50.

5.2 简化密钥攻击过程实验

在本实验中, 我们仅使用密钥攻击过程的第一步进行密钥恢复, 也即仅利用Cut1值进行密钥恢复.首先猜测一个最后一轮密钥, 解密一组密文数据, 然后用3 面体神经网络区分器N9 和单差分神经网络区分器N9 分别去预测, 给出该组密文数据的预测值分布, 最后利用贝叶斯优化方法搜索候选子密钥, 当wk>Cut1时, 认为该密钥为最终密钥. 两种区分器所得结果如表4.

表4 单差分神经网络区分器和三面体神经网络区分器密钥恢复精度对比Table 4 Comparison of key recovery accuracy between single differential neural network distinguisher and polytopic differential neural network distinguisher

数据结构个数取512 和32 是为了保证可用差分结构个数约为2. 主循环次数分别为128 和1024. 通过对比发现, 在仅用Cut1值进行密钥恢复时, 单差分区分器几乎很难将正确密钥筛选出来, 3 面体区分器在数据复杂度和计算复杂度一定增加的情况下, 可以以30% 的比例正确恢复密钥. 其原因是3 面体对数据条件的要求更为严格, 区分器精度更高.

在无概率攻击实验和简化密钥攻击过程实验中, 我们都直接指定了进入两种神经网络区分器的可用差分结构个数, 但是在实际攻击中, 我们需要考虑得到可用差分结构个数的概率, 此概率直接影响实际攻击的数据复杂度.

5.3 多面体和单差分神经网络区分器密钥恢复效果对比

为了对比单差分神经网络区分器和3 面体神经网络区分器精度对密钥恢复的影响,我们利用两种神经网络区分器进行了13 轮密钥恢复攻击. 三面体差分密钥恢复攻击采用3 面体神经网络区分器N9 和N8.单差分密钥恢复攻击采用单差分神经网络区分器N9 和N8. 单差分攻击取20 个明文结构, 3 面体攻击取320 个明文结构, 即能够基本保证有一个可用差分结构. 主循环次数采用数据结构数的4 倍. 3 面体差分13 轮密钥恢复攻击时,数据复杂度为28.5×3×64 ≈215.9,估计时间复杂度为(l1+l2)×22×22×217≈227.3,其中,l1≈20,l2≈66. 3 面体差分13 轮密钥恢复攻击时, 数据复杂度为28.5×3×64 ≈215.9, 估计时间复杂度为(l1+l2)×1.5×22×22×217≈231.4, 其中,l1≈315,l2≈549.

在该实验的基础上将数据结构个数增加, 结果如表5. 通过对比可见, 在数据复杂度和时间复杂度一定增加的情况下, 采用多面体神经网络区分器提高密钥恢复成功率的效果有限.

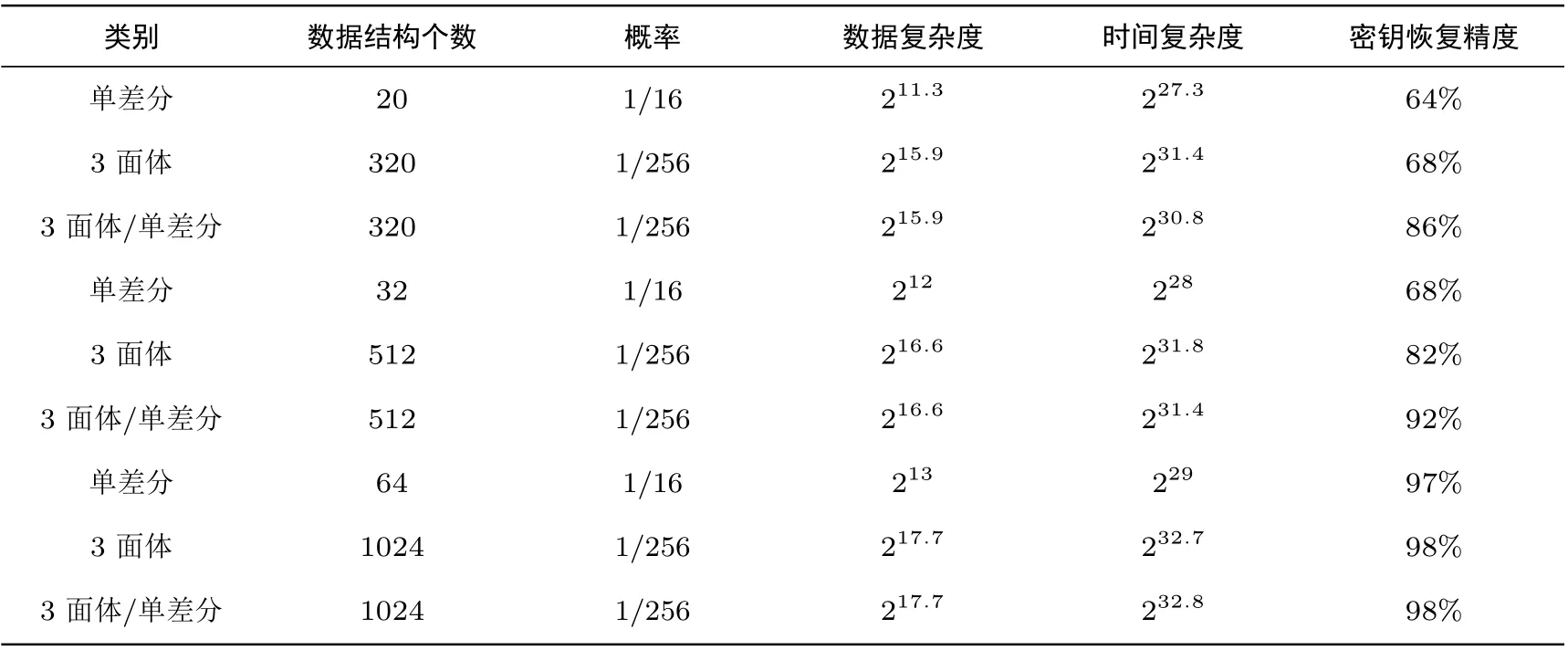
表5 神经网络区分器不同使用方式密钥恢复效果对比Table 5 Key recovery accuracy comparison of neural network distinguisher using different methods

5.4 混合使用多面体和单差分神经网络区分器

上一个实验中, 3 面体攻击的两个步骤均使用3 面体神经网络区分器, 本实验中, 3 面体攻击的第一步使用3 面体神经网络区分器N9, 第二步使用单差分神经网络区分器N8. 主循环次数采用数据结构次数的4 倍. 用“3 面体/单差分” 表示3 面体和单差分的混合, 在第4 节实验基础上, 增加其它数据结构数目, 结果如表5.

由对比可知, 在可用差分结构数目相近的情况下, 混合使用3 面体差分区分器和单差分区分器, 可以使密钥恢复成功率相较于单差分区分器有一定提高, 但相应数据复杂度和计算复杂度也有增加.

6 结束语

本文主要提出了基于深度学习的多面体差分攻击方法, 并通过对Simeck32/64 算法的实际密钥恢复攻击, 说明了多面体差分攻击方法的应用及效果. 在实际密钥恢复攻击过程中, 我们使用了多面体神经网络区分器、单差分神经网络区分器以及两种区分器的混合. 与传统差分攻击方式相比, 三种攻击方式均可降低数据复杂度和时间复杂度. 同时, 相对于单差分神经网络区分器, 多面体差分神经网络区分器进行密钥恢复的成功率略好, 但所需数据复杂度和计算复杂度较高, 在两种区分器混合使用的情况下密钥恢复成功率和数据时间复杂度取得了较好平衡. 最后, 虽然这几种神经网络区分器及其应用方式都具有一定的局限性, 如攻击多轮算法时区分器精度不高等, 但是作为一种新的密码分析工具, 值得我们继续探索.