并发L-BFGS异构率定算法设计与实现

田在荣 李强 聂宁明 全婷

摘要：针对分布式水文模型在水文模拟参数率定过程中计算与收敛速度过慢的问题，提出一种面向异构平台的水文模拟并发参数率定方法。对传统的L-BFGS算法进行并发式改造使其结构适应并行计算的率定需求;对HIMS水文模型进行异构移植，使整个水文模型以多线程的形式并发运行于协处理器端;以拉萨河流域为例，在Intel+Nvidia GPU与国产AI加速器的双异构平台部署模型与测试算例。测试结果表明，并发L-BFGS异构率定算法适用于当前主流的“处理器+协处理器”架构，并能够得到较好的率定效果。

关键词：水文模拟;参数率定;HIMS;异构移植

中图分类号：TP 338.6 文献标志码：A

文章编号：1006-1037（2021）03-0043-08

水文模型是对大自然中复杂的水文现象在计算机中的抽象化和概念化的展现[1]，是人们认识复杂的水循环运动过程和机制下的有效方法和手段。水文模型由众多的物理模型如降雨入渗、蒸发散发、产流回流等具有特定物理意义的物理模型构成[2]，其中大多数物理模型都包含一系列流域相关的待定参数，而对水文模型进行参数率定就是通过确定当前所研究流域的待定参数值，最终完成对当前流域的建模。因此对模型参数率定是水文模拟过程的重要组成部分，参数选取的优劣直接影响到最终的模拟精度。而参数率定由于计算量大、耗时长，一直以来都是领域专家所必须面对的问题之一。早期研究水文模型时，参数率定的方法主要以人工试错法[3]、自动优选参数法[4]为主。人工试错法是根据以往积累的经验选取一组参数，代入水文模型进行模拟计算，得到河流径流量的模拟值，与观测值对比，然后调整参数的取值，继续对比模拟值和观测值，直到模拟值和观测值的误差在允许的范围，该组参数即为所求的最优参数组。人工试错法受人为主观影响较高[5]，且率定效率较低，实用性较差。自动优选参数法是通过设定计算机程序，使计算机根据设定的规则选取参数进行率定[6]。由于水文模型的运行依赖于流域内每个子流域内部众多物理模型的参数取值，本身对水文模型具有约束性，水文模型中各个参数具有相对独立性，因此自动优选法的应用存在一定困难。随着计算机科学以及人工智能的不断发展，一些自动寻优算法[7]应用在参数率定中。由于复杂的水文模型的参数个数很多（如SWAT模型有大约200个[8]），使得模型的计算量会随着参数维度的增加，呈现指数型增长[9]，从而陷入“维数灾难”[10]。因此，面对大规模流域模拟，传统的计算方式已经难以适应当前的计算需求。高性能计算技术的发展使超算领域进入了新的时代。CPU+GPU加速器混合异构架构在高性能计算机中逐渐成为新的发展热点[11]，如2019年世界超级计算机500强（TOP500）榜首—美国的Summit超算使用的是CPU+GPU混合异构架构。使用高性能异构计算方式来解决工程中遇到的算力匮乏问题已经成为主流，而对于水文模拟参数率定这种具有天然并行性的高计算需求的应用[12]，如何利用异构计算的强大算力解决计算需求，已经成为当前该领域亟待解决的问题之一。在超算平台上进行水文计算，必须要发展相应的异构算法，高效利用超算平台的计算资源。本文选取具有较强收敛能力的L-BFGS算法作为基础率定算法[13]，挖掘其搜索方向及步长的选取原理[14]，在保留算法总体搜索方式的基础上对其进行并发式改造，使算法具备并发处理多个搜索线路的能力[15]。本文选取适用于中国大多数大江大河及各种流域的HIMS（hydroinformatic modeling system）水文模型[16]作为主要参考模型，通过对模型本身计算热点的分析，确定适合协处理器计算的部分，并对这一部分进行异构化改造，使得模型的实际运行由CPU端发起，通过各种CPU和协处理器间的数据拷贝，使计算热点全部运行于协处理器，利用协处理器强大的并发计算能力，在保证计算精度的同时大幅减少计算时间。最后对两种目前较为常见的异构平台做了相应的算法测试与对比。

2 并发L-BFGS算法在参数率定中的应用

2.1 水文模型参数率定的评价依据

应用水文模型模拟水文工作时，关键的一项就是寻找水文模型的最优参数组，水文模型模拟的精度很大程度上取决于模型中参数组的选择。参数率定的目标是为待研究流域的各个子流域寻找到一组“最优”的参数组，使得应用该参数组进行水文模拟后的模拟值和实际观测值的差距最小。通常，参数率定结果的优劣使用Nash（Nash-Suttcliffe，后面简称Nash）系数作为判定依据。Nash系数越接近于1，模拟值和观测值差距越小。Nash系数为

其中，Qo表示观测值，Qm表示模拟值，Qt表示在第t时刻的某个值。

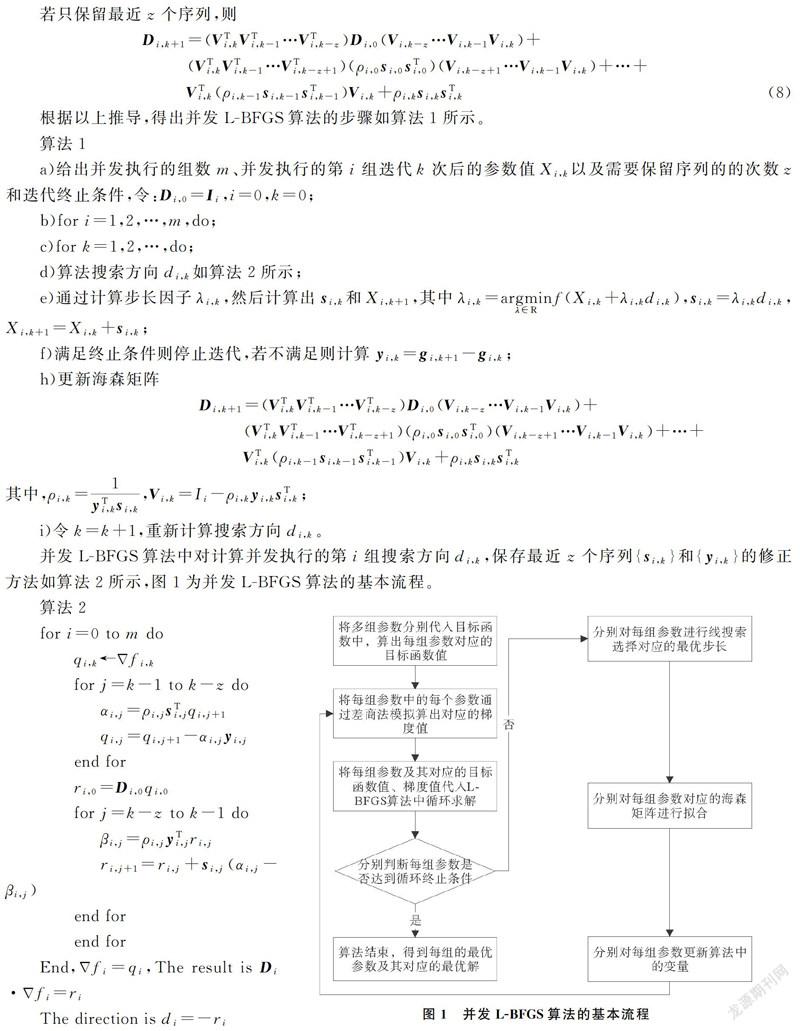
2.2 L-BFGS算法的并发执行

差商法求导的步骤如下：

将L-BFGS算法所需要的m组初始值、目标函数值和初始值对应的梯度值代入算法中，就可以通过多次迭代找到最优的m个Nash系数。

2.3 HIMS模型的异构移植

HIMS模型是国内自主研发的流域分布式水文模型，具有完全的知识产权。主要应用在流域内评价、规划和管理水资源，以及处理与水相关的生态环境保护工作[17]，如洪水预报、管理水污染与侵蚀以及气候变化等。HIMS具有多源信息融合、数字流域分析、分布式模拟以及模型定制等功能[18]，可以针对国内各个流域不同的水文尺度、流域空间非均一性[19]以及不同的自然和人文环境进行水循环模拟、参数率定等水文工作。目前，HIMS模型已应用并部署于国内外众多流域的水文模拟过程中，并取得了良好的应用效果。

HIMS模型最初是面向CPU端开发，并运行于PC机环境，对于大规模异构计算，需要对HIMS整体架构进行调整。根据目前的协处理器体系结构，原HIMS模型中用于读取原始数据而开辟的存储空间需要在计算前全部转移到device端，并在计算结束后将Nash系数作为结果传回host端。传入的数据除原始数据如降雨量、最高最低温度、海拔、流域面积等，还有已经在host端生成的由m组n维参数组成的数组（x1，1，x1，2，…，x1，n，…，xm，1，xm，2，…，xm，n），并在device端使用線程ID作为标识将参数组分割至m个不同线程。HIMS模型的核心是产流和汇流（即马斯京根过程）两大部分，从CPU到协处理器的移植过程包括将涉及的函数定义成device，原始模型中所有的global类型变量、指针全部通过核函数传入device，模型内部用到的所有变量的内存大小需调整为原先的m倍。计算完之后，使用得到的m组模拟值和实测值通过计算得出m个Nash系数并传出。图2和图3分别为HIMS原始工作流程和HIMS在异构平台工作流程。

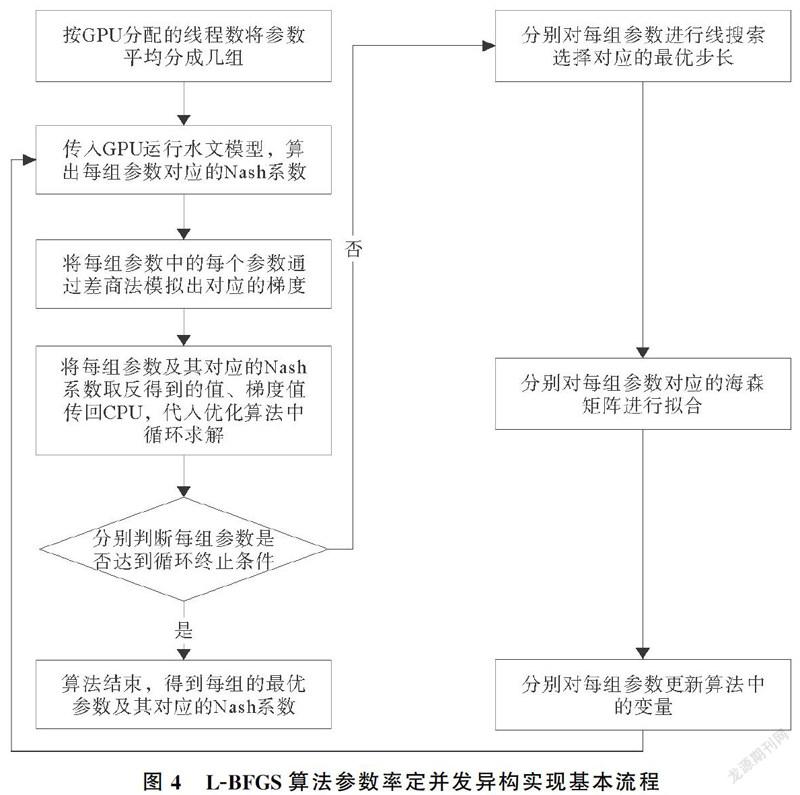
2.4 并发L-BFGS算法的异构实现

并发L-BFGS算法在参数率定中的并发异构实现是通过CPU和GPU协同工作的。首先，CPU同时通过随机函数产生m组n维参数（x1，1，x1，2，…，x1，n，…，xm，1，xm，2，…，xm，n），将m组n维参数传入GPU中，按照线程号平均分成m组，每组分别运行HIMS水文模型，得到每组对应的Nash系数，然后将m组参数及其对应的Nash系数取反传入CPU端，通过差商求导模拟出每组参数每个位置的梯度，将这些变量代入优化算法经过多次迭代，分别判断每组参数是否达到迭代终止条件，最后得到m个最优参数组和最优Nash系数。L-BFGS算法并发异构实现的基本流程如图4所示。

3 数值实验

本节对HIMS模型的异构移植以及并发L-BFGS算法在水文模拟具体参数优化过程进行数值实验，并比较和分析数值实验结果，探讨异构移植的效率和并发性能以及并发L-BFGS算法在参数率定中的具体应用。运行环境为配置V100的GPU服务器和配置国产AI加速器的国产先进计算平台，实验数值均为运行5次计算得出的平均值。

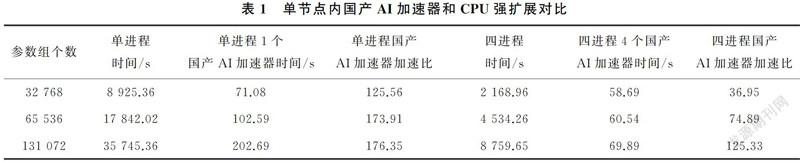
（1） 单节点内国产AI加速器和CPU在参数率定中的并发性能测试。实验设置参数组个数设置为32 768（1 024×32）、65 536（1 024×64）和13 1072（1 024×128）。由表1，国产AI加速器程序和CPU程序相比，单进程运行时，加速比在125以上，加速效果较为理想，且随着参数组规模增加，加速比逐渐升高，其中参数组个数从65 536增加到131 072的计算时间从102.59 s增加到202.69 s，说明算例在65 536时基本达到国产AI加速器的满载状态，这也与国产AI加速器内含64核、每核支持1 024线程的硬件架构相符。在四进程运行时，保持总参数组数量32 768、65 536、131 072不变，将每进程参数组数量降为原先的四分之一，CPU运行时间约为原先的四分之一，说明强扩展性良好，而国产AI加速器的时间从58.69 s到69.89 s变化不大，说明国产AI加速器的线程还没有到达计算临界条件。

从表2中可以看出，在保持每进程以及每个国产AI加速器参数组个数不变时，单进程运行和四进程运行以及单进程1个国产AI加速器和四进程四个国产AI加速器的运行时间相差不大，说明扩展性较好。

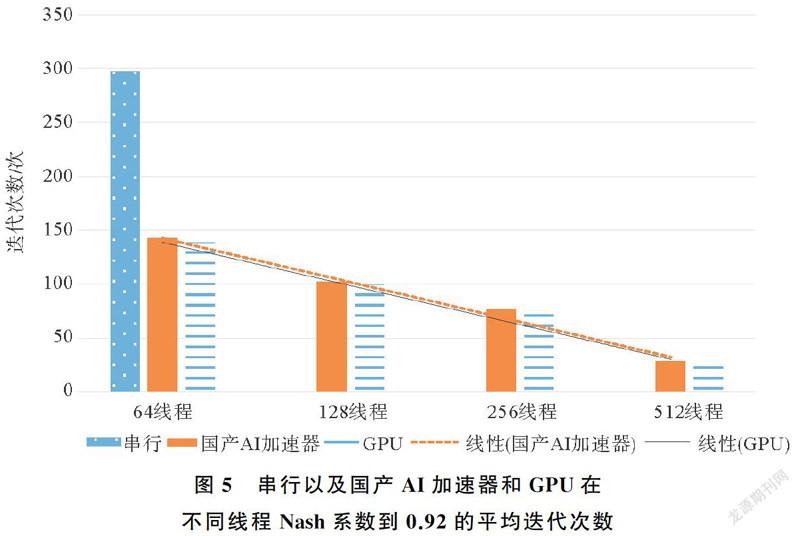
（2） L-BFGS算法在串行程序以及异构平台的国产AI加速器和GPU程序在不同线程Nash系数计算到0.92的迭代次数变化情况。由图5可知，传统的L-BFGS算法（即串行实现）在进行参数率定时，迭代次数约在297次Nash系数才能到达0.92，而L-BFGS算法在GPU和国产AI加速器这样的异构平台进行多线程并发参数率定时，Nash系数到达0.92的迭代次数随着线程数增加而逐渐减少。在512线程时只需要迭代大约27次即可使Nash系数到达0.92，说明L-BFGS算法在多线程并发实现较之串行实现时，迭代次数大幅度减少，实现了L-BFGS算法提高率定效率的任务。而在相同线程时，GPU的迭代次数略少于国产AI加速器的迭代次数，说明V100的计算性能略优于当前国产AI加速器的计算性能。

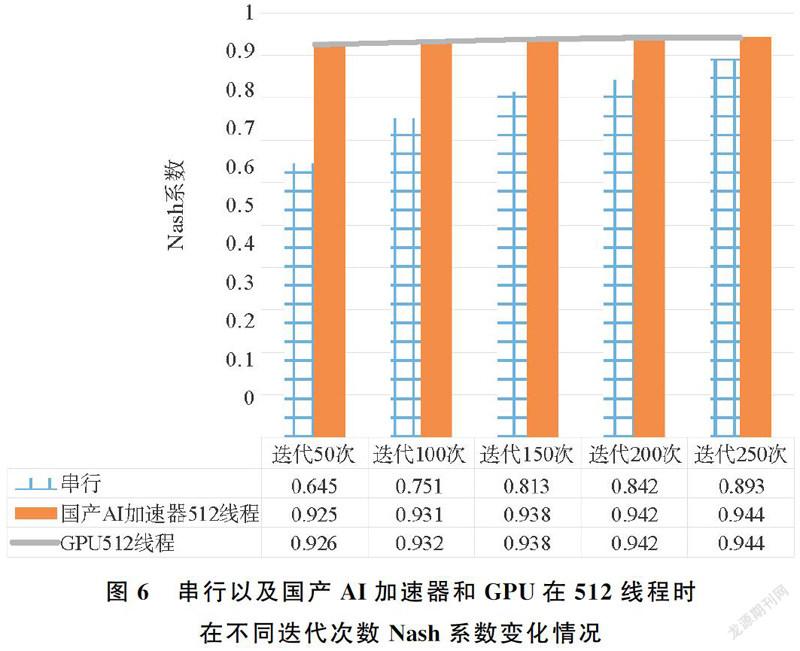
（3） L-BFGS在串行时以及国产AI加速器和GPU在512线程时在不同迭代次数Nash系數变化情况。由图6，L-BFGS算法在异构平台的GPU和国产AI加速器实现较之其串行实现在相同迭代次数时，Nash系数要远大于串行实现，说明，异构运行实现了提高Nash系数精度。而国产AI加速器和GPU在512线程时迭代到200次之后，Nash系数基本保持在0.94左右。

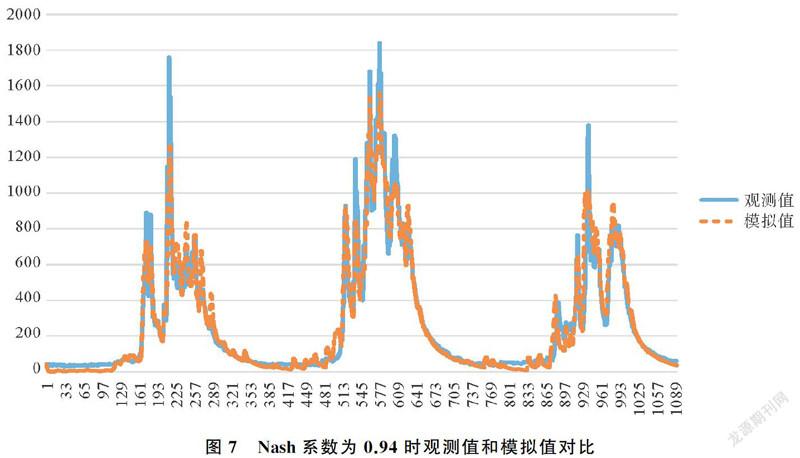
（4） Nash系数为0.94时观测值和模拟值对比。由图7，当Nash系数为0.94时，通过水文模拟出来的径流量模拟值总体趋势上贴近观测值，说明通过L-BFGS算法的参数率定使参数集靠近最优参数集，通过这组最优参数集水文模拟出来的径流量也会与观测值更加贴近。

4 结论

本文通过对传统L-BFGS算法进行并发式改进，并将HIMS水文模型进行异构移植，得到了一套面向异构平台的大规模并发率定算法。针对HIMS模型的参数优化实验表明，并发L-BFGS算法的异构实现较之串行实现迭代次数有了大幅度减少，且Nash系数的精度也有了较为明显提高。

参考文献

[1]刘海帆.基于过程的大尺度水文模型的层级敏感性分析及其在亚马逊流域中的应用[D].北京：中国地质大学，2020.

[2]QI W， LIU J. Studies on changes in extreme flood peaks resulting from land-use changes need to consider roughness variations[J]. Hydrological Sciences Journal， 2019， 64（16）：2015-2024.

[3]栾承梅.流域水文模型参数优化问题研究[D].南京：河海大学，2005.

[4]郭靖，郭生练，胡安焱，等. 基于TOPSIS法的水文模型多目标参数自动优选方法研究[J].水电能源科学， 2006， 24（6）：25-28.

[5]徐帅帅.基于分布式水文模型的洪水预报及水库削峰的案例研究[D].济南：山东建筑大学，2019.

[6]张洪刚，王金星，刘攀，等. 概念性水文模型参数自动优选方法的比较研究[J].石河子大学学报（自然科学版），2002（3）：229-232.

[7]李月玉，李磊，等. 免疫粒子群算法与支持向量机在枯水期月径流预测中的应用[J].水资源与水工程学报， 2015（3）：124-128.

[8]许自舟， 周旭东， 隋伟娜，等. 基于SWAT模型的碧流河流域入海径流模拟研究[J]. 海洋环境科学， 2020，39（2）：216-222.

[9]崔东文，郑斌.几种智能优化算法与支持向量机相融合的月径流预测模型及应用[J].人民珠江，2016， 37（3）：18-25.

[10] 马彦斌，盛旺，李江云，等. 基于遗传算法的SWMM模型参数率定研究[J].中国农村水利水电，2020（7）：46-49.

[11] 张军华， 臧胜涛， 单联瑜，等. 高性能计算的发展现状及趋势[J]. 石油地球物理勘探， 2010（06）：918-925.

[12] 高明，程相国，咸鹤群，等.移动端代替算法的并行优化[J].青岛大学学报（自然科学版），2016，29（3）：53-58.

[13] CHEN W， WANG Z， ZHOU J. Large-scale L-BFGS using MapReduce[J].Advances in Neural Information Processing Systems， 2014（2）：1332-1340.

[14] KEARSLEY A J. Matrix-free algorithm for the large-scale constrained trust-region subproblem[J]. Optimization Methods &; Software， 2006， 21（2）：233-245.

[15] 于一超，田志遠，刘相静，等.非线性互补问题的一个数值解法[J].青岛大学学报（自然科学版），2014，27（3）：14-18.

[16] 刘昌明，郑红星.基于HIMS的水文过程多尺度综合模拟[J].北京师范大学学报（自然科学 版），2010，46（3）：268-273.

[17] 尚瑞朝，王娟.HIMS系统模型在洪水预报中的应用[J].浙江水利科技，2015，43（4）：9-12.

[18] JIANG Y， LIU C， LI X. Hydrological impacts of climate change simulated by HIMS Models in the Luanhe River Basin， North China[J]. Water Resources Management， 2015， 29（4）：1365-1384.

[19] 吴潇潇. HIMS模型在曹江流域流量变化过程模拟中的应用[D].淮南：安徽理工大学，2016.