基于多子网复合复杂网络模型的级联失效研究

贾宁 宾晟 孙更新

摘要：针对目前耦合网络级联失效的研究方法仅限于单个关系的问题，根据多子网复合复杂网络模型构建复合网络，结合多种关系研究了复合网络级联失效问题，考察在不同影响因素下，网内关系和加载关系对网络鲁棒性的影响。研究结果表明，网内关系和加载关系共同影响着网络级联失效的过程及规模，复合网络中两子网拓扑结构不同，网内关系对网络的影响不同;加载关系强度占比越大，网络鲁棒性越强。关系强度比例对网络故障规模存在决定性影响。

关键词：级联失效，耦合网络，多关系网络，多子网复合复杂网络模型，鲁棒性

中图分类号：TP391

文献标志码：A

文章编号：1006-1037（2021）03-0028-10

随着科学技术的进步，系统科学[1-3]蓬勃发展，给人们带来了巨大便利。由于网络自身存在脆弱性，在蓄意攻击和随机失效的打击下很容易发生级联失效事故。例如2003年意大利全国大停电事故[4]，2008年中国南方电力网络崩溃事故[5]和因拥堵造成的互联网崩溃事故[6]等，研究发现这类事故都是由故障通过耦合关系在网络之间反复传播，导致网络大面积瘫痪，所以耦合网络级联失效的研究对于维持网络系统的稳定具有重要意义。Buldyrev等[7]以双层一对一耦合的网络为例，发现耦合网络级联失效现象不同于单个网络，开启了耦合网络级联失效研究的先河。目前耦合网络级联失效的研究主要分为三类：基于两侧节点一对一耦合的网络[7-19]、一对多和多对多耦合的网络[20-25]。对于两侧节点一对一耦合的网络，Chen等[8]研究了不同的耦合方式对耦合网络鲁棒性的影响，发现异配耦合方式下网络鲁棒性最优;李甍娜等[9]研究了在负载作用下不同耦合方式的相依网络鲁棒性，发现同配耦合方式下网络鲁棒性最强;陈世明等[10]研究了不同耦合比例和耦合强度对耦合网络的鲁棒性影响，提出了構建全局同质化的耦合模式，有效改善了耦合网络鲁棒性;杨程成等[11]研究了耦合网络在耦合关系变化下的鲁棒性，发现网络之间度数相似的节点耦合概率越大，网络鲁棒性越高;陈世明等[12]以一对一全耦合和部分耦合的网络模型为例，分别提出了低相对介数内加边策略和低相对介数耦合加边策略，显著提升了耦合网络的鲁棒性。关于两侧节点一对多和多对多耦合的网络，Shao等[20]提出了具有多个支持依赖关系的耦合网络模型，发现与一对一相互依存关系相比具有更高的鲁棒性;Fu等[21]研究了耦合网络中依赖关系的方向性、冗余性和依赖程度对鲁棒性的影响，发现基于有向依赖的网络鲁棒性要低于无向依赖的网络鲁棒性。陈世明等[22]基于典型的复杂网络拓扑模型，建立了对称和非对称的耦合网络模型，研究了网络鲁棒性与耦合强度之间的关系，发现提高或减小耦合强度，网络鲁棒性不会单调地增强或下降。彭兴钊等[23]，提出了耦合边和内部边与初始负载相关联的级联失效模型，发现当外部度和内部度对负荷贡献比达到一定值时， 网络鲁棒性最强。综上所述，目前耦合网络级联失效的研究都基于层次网络模型，描述了多类个体及其层间的相互关系，仅能描述具有层次关系的对象问题，无法描述处于同一层次且彼此具有多种关系的个体，在现实中，系统的个体之间不只存在层次关系，而多子网复合复杂网络模型可以描述不同类个体间的关系以及同类个体间的多种关系，基于该模型，结合多种关系提出了复合网络级联失效的研究，重点考察在不同影响因素下，网内关系和加载关系对网络鲁棒性的影响。

1 模型构建

1.1 复合网模型

根据多子网复合复杂网络模型[26]初始构建的两个向量复合网分别用ΣA=（GA，SA，MA）和ΣB=（GB，SB，MB）表示，其中GA=（VA，EA，RA，FA），GB=（VB，EB，RB，FB），GA和GB表示复合网A和B，VA和VB表示节点集合，EA和EB表示连边集合，RA和RB表示复合网内的节点之间相互作用关系的集合，FA和FB表示连边和关系的映射，其中，FA∶EA→RA，SA和SB表示复合网A和B的关系强度向量空间，MA和MB表示连边和关系强度向量空间的映射，其中MA∶EA→SA。

1.2 耦合网络级联失效模型

本文以容量—负载模型及两侧节点一对一耦合的网络为例，构建典型的耦合网络级联失效模型。

首先构建两个子网络，分别记为网络A和网络B，节点总数分别为NA和NB，每个子网络中节点的内部连接定义为连接边，网络A与网络B之间的节点连接定义为耦合边，令网络A和B之间的节点一对一随机耦合且相互依赖。

节点度衡量了节点在网络中的重要程度，度大的节点往往承载大量的负载，节点vh的初始负载根据度函数来定义

其中，Lvh（0）表示节点vh的初始负载，kvh为节点的度，α，β（α，β1）是可调参数，控制初始负载的强度。

节点容量衡量了每个节点可承受负载的大小，节点容量越大，越不容易过载失效，整个网络抵御级联失效的能力越强。节点容量定义与初始负载呈正相关

其中，λ（λ>0）表示容限系数，λ越大节点容量越大，其抵御级联失效的能力越强，但相应的成本也越高。

假设网络A中节点遭受攻击而失效后，其自身负载会根据一定的比例分配给邻居节点，节点vh为失效节点，节点vl为该节点的一个邻居，本文以局部择优分配方式为例，令失效节点分配给邻居节点的负载为

其中，Γvh表示节点vh邻居节点的集合，△Lvhvl表示节点vh分配给节点vl的负载量。

当节点vl所接收的负载加上它的初始负载大于自身容量

节点vl失效，负荷进一步重新分配，将负载重分配给邻居节点，节点vl接收到分配过来的负载后过载失效，其负载继续分配给它的邻居节点，故障在网络A中传播开来。节点失效后将失去全部耦合边，由于网络A与B相互依赖，如果网络B中节点在网络A中的耦合节点全部故障，则节点失效，根据式（3）将自身负载传递给邻居节点，如果邻居节点过载失效，则故障从网络A传播到网络B中，反过来，当网络A中节点在网络B中的耦合节点全部失效时，节点故障，其自身负载传递给邻居节点，故障从网络B传回网络A中，该过程循环，当整个网络没有节点故障时，级联失效过程结束，如图2所示。

在图2中，左侧为网络A的节点，右侧为网络B的节点，网络内部的节点之间都存在连边，网络A和B的节点之间只存在一条耦合边。图2（a）在初始状态下，整个网络处于稳定状态;图2（b）网络A中的节点A4遭受攻击，移除节点A4所有的连边，网络B中的节点B4失去所有耦合边后失效。将节点A4与B4的负荷沿着虚线以及根据式（3）的负荷分配规则分别分配到各自的邻居节点中。图2（c），假设只有节点B5过载失效，移除该节点的全部连边，节点A5因失去节点B5的耦合边而失效。图2（d）所有节点均有耦合边，且承受负荷均小于容量，级联失效停止，耦合网络达到稳定状态。

1.3 复合网级联失效建模

与基于层次网络模型的级联失效建模不同，复合网级联失效建模不光要考虑不同类个体间的关系，还要考虑到同类个体间的多种关系。如果把节点间的关系看作线路，则负载的传输会经过不同的线路，其中，每条线路都存在流量限制，表示单位时间内负载通过该线路的负载量，通常流量与连边两端节点的度呈正相关，设连边vhvl关于关系ri的流量为

节点承载负荷的大小受网内关系的影响，与流量呈正相关，由于存在加载关系的影响，只考虑网内关系不合适。通常情况下，当与节点带有加载关系的连边数量越多，且这些节点的网内关系度越大，节点承担的负载越大，所以定义子网A内节点vh的初始负载

节点容量的大小受节点间多种关系的影响，初始负载的定义通过流量描述了关系对节点的影响，所以节点容量仍与初始负载相关联，故采用式（2）定义。相关文献的负载重分配策略普遍使用局域择优重分配，由于该方法不能识别关键节点，很容易导致桥节点失效，产生更严重的损坏，所以本文提出根据节点重要性来分配负载，节点越重要，分配的负载越少，反之越多，首先定义连边vhvl关于关系ri的重要性

其中，privhvl表示由连边vhvl根据关系ri组成的三角形数量。

如果要判断节点vh关于关系ri重要性，不仅要考虑连边的重要程度，也要考虑节点vl对连边vhvl的重要程度，定义erivhvl（vl）

假设子网A中节点vh因遭受攻击而失效，设节点vl为其在子网A中的一个邻居，则失效节点分配给节点vl的负载

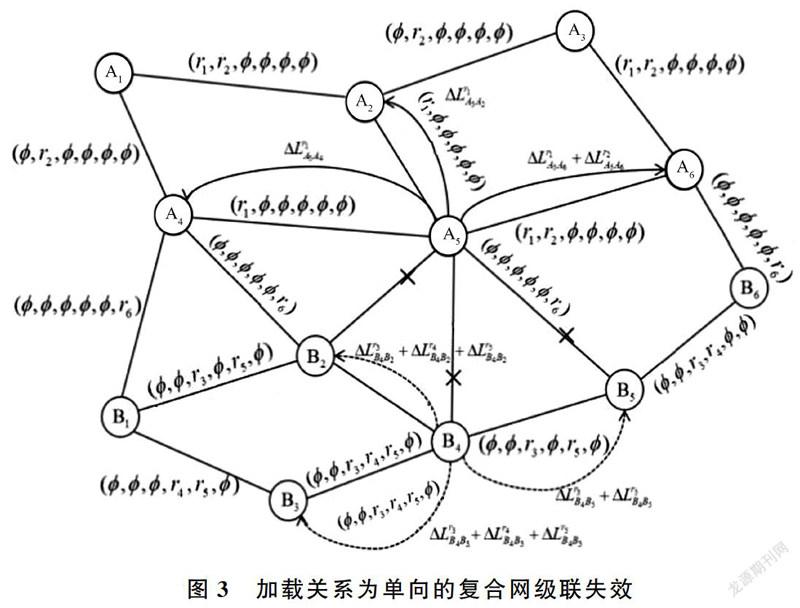
则节点故障，其自身负载根据上述方式分配给它的邻居节点，故障在子网A中传播开来。如果向量复合网中只存在子网络A和B，且加载关系为子网络B单向依赖于A，则当子网B中节点在子网A中与加载关系相连的节点全部故障时，则该节点失效，同理，其自身负载根据式（9）传递给它的邻居节点，故障从子网A传播到子网B中，直到子网B中没有节点失效为止，该过程如图3所示。

子网A中节点A5遭受攻击而失效，其自身负载根据网内关系分配给它的鄰居节点，同时断开与该节点相连的带有加载关系的连边，子网B中节点B4因失去全部带有加载关系的连边而失效，其自身负载根据网内关系分配给它的邻居节点。

综上所述，可以看出一个节点发生故障的原因：网内关系导致的传播故障以及加载关系导致的故障。

为了更好的描述整个网络中每个节点的状态，本文对每个节点定义一个过载函数值Gk，相当于对每个节点分配一个动态权重，表示节点过载的难度，假设网络中每个节点只有‘正常’和‘失效’两种状态，1表示所有节点处于正常状态，0表示节点处于失效状态，所以节点v的过载函数设为

即不用移除节点就能显示整个网络的状态。

初始仅仅攻击子网A中的一个节点，并在级联失效结束后计算CFv（这里的CFv表示为由节点v所导致的失效节点数量），显然，0≤CFv≤N-1，为了量化整个网络的鲁棒性，攻击子网络A中全部节点，再将失效节点数量进行归一化处理

其中，CFv=FA+FB，FA表示级联失效结束后子网A失效节点总和，FB表示子网B失效节点总和，S为移除子网A中所有节点导致的整个网络失效节点总和的归一化处理值，即网络损坏规模。S越大网络抵御级联失效的能力越弱，S越小网络抵御级联失效的能力越强，网络鲁棒性越强。

2 仿真分析

在实验中，首先构建复合网络A和B，网内关系分别设为r1和r2，以复合网A为基底网，在加载关系r3下，将复合网A加载到B中，其加载关系为子网络B单向依赖于A，构建新的向量复合网，以该网络为例，攻击子网络A中每一个节点，将失效节点数量进行归一化处理得出S值，如式（13），通过调节节点的容忍系数λ和选取不同的关系强度比例参数sf1：sf2：sf3来进行仿真实验，重点考察在不同影响因素下，关系强度对复合网的影响，本文根据上述建立的级联失效模型，考虑过载失效和加载关系失效两种模式，制定了模拟复合网级联失效过程的算法：

a）攻击子网A中的节点v使其失效，将该节点的过载函数值记为“0”，并找出与v相连的邻居节点;

b）对节点v和其邻居节点的负荷进行重分配，有节点过载则将其过载函数记为“0”;

c）找出子网A中的失效节点;

d）找出其中一个失效节点的全部邻居节点，对失效节点和其邻居节点进行负载重分配，其中，过载函数值为“0”的节点不再接受外来负荷，有节点过载则将其记为“0”;

e）重复步骤c）～d），直到没有节点失效;

f）计算整个网络中失效节点的数目记为FA;

g）找出子网B中与子网A有加载关系连接的节点，如果该节点在子网A中带有加载关系相连的节点全部失效，则将其过载函数记为“0”;

h）找出子网B中的失效节点;

i）对子网B中的一个失效节点及其邻居节点进行负载重分配，其中，过载函数值为“0”的节点不再接受外来负荷，节点失效后将其记为“0”;

j）重复步骤h）～i），直到没有节点失效;

k）计算整个网络中失效节点的数目记为FB;

l）重复步骤a）～k），直到完成对子网A中每个节点进行一次攻击，计算复合网的故障规模S。

2.1 拓扑结构不同条件下网内关系对网络的影响

在网络中，如果每个子网的拓扑结构不同，在节点间关系强度作用下，网络中发生的故障现象不同于以往的研究，由于实际网络系统倾向于WS小世界网络和BA无标度网络，因此为了探究在网内关系拓扑结构不同条件下，关系强度对网络级联失效的影响，本文根据上述网络拓扑分别进行对比实验。

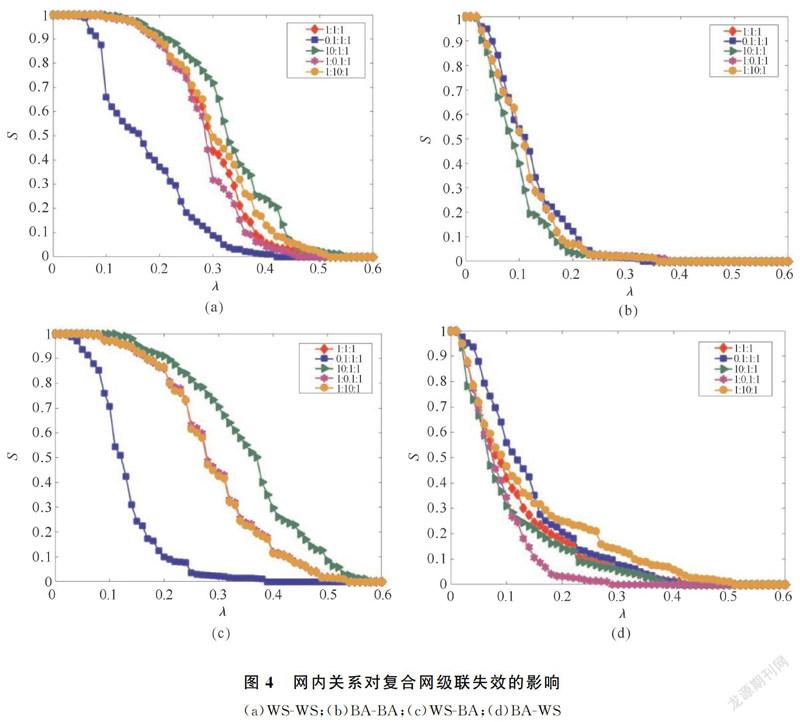
首先，构建节点总数为200，子网络A和B平均度为2的复合网，令两子网节点之间随机建立加载关系，加载关系平均度为2，设参数α=β=1。S代表鲁棒性测度，如式（13），λ表示节点的容忍系数，如式（2），当关系强度比例参数取不同值时，得出的S-λ曲线如图4所示。

在图4（a）中，随着网内关系r1，r2关系强度占比的缩小，网络鲁棒性随之增强;反之，二者关系强度占比增大时，网络鲁棒性下降;其中，关系r1对网络作用明显，当关系强度占比足够小时，网络鲁棒性最强。在图4（b）中，调节网内关系r1，r2强度占比，发现网络故障规模变化微小，说明在拓扑结构为BA-BA的网络中，网内关系对网络没有影响。在图4（c）中，减小网内关系r1强度占比，网络鲁棒性明显增强;而关系强度比为1∶1∶1、1∶0.1∶1、1∶10∶1的曲线相互重合，关系r2对网络没有影响。说明在WS-BA的网络中，除加载关系外，网络故障规模受提供依赖关系的子网影响。在图4（d）中，增大网内关系r2强度占比，网络鲁棒性明显增强;而增大和减小关系r1的强度占比，其曲线和关系强度比例为1∶1∶1的曲线重合。说明在BA-WS的网络中，除加载关系外，网络故障规模受被提供依赖关系的子网影响。

2.2 拓扑结构不同条件下加载关系对网络的影响

上述实验主要探究了网内关系对网络的影响，与此同时，子网之间存在加载关系，加载关系强度越强，节点受其它子网的影响越大，网络中发生的故障现象会有所不同。因此为了探究在拓扑结构不同条件下，加载关系对网络级联失效的影响，本文根据WS，BA的网络拓扑结构，以不同的组合分别进行实验。

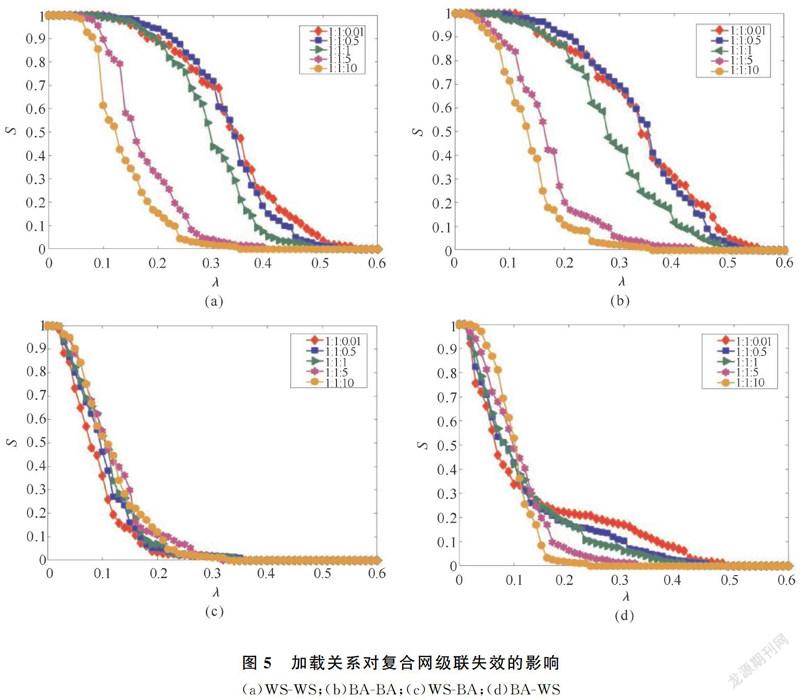
首先，构建节点总数为200，子网络A和B平均度为2的复合网，令两子网节点之间随机建立加载关系，加载关系平均度为2，设参数α=β=1，当加载关系强度占比取不同值时，得出的S-λ曲线如图5所示。

在图5（a），（c），（d）中，随着加载关系r3强度占比的增大，网络鲁棒性随之增强，说明加载关系有利于网络鲁棒性的提高;在，5（b）中，增大加载关系强度占比，网络变化微小，说明在BA-BA的网络中，加载关系对网络没有影响。因此在现实中，为了提高网络抵御级联失效的能力，要盡可能地增强子网间的影响力。

2.3 网内关系平均度不同条件下网内关系和加载关系对网络的影响

网络平均度越大，网络鲁棒性越强。复合网是由多个子网络复合而成的，如果每个子网的网内关系平均度不同，在关系强度作用下，网络中发生的级联失效现象会出现不同的性质，因此为了进一步研究，在两个平均度取不同值的子网络构成的网络中分别进行实验。

首先，构建拓扑结构为WS的子网络A和B，子网络节点总数都为200的复合网，参数α，β为1，令两子网节点之间随机建立加载关系，加载关系平均度为2，子网的网内平均度分别设为2，4，6，根据不同的组合，当关系强度比例参数取不同值时，得出的S-λ曲线如图6所示。

可知，无论网内关系平均度取何值，加载关系强度占比越大，网络鲁棒性越强。在图6（a）和（b）中，关系r1强度占比越小，网络鲁棒性越强;关系r2强度占比为0.1和10的曲线几乎重合，说明子网B网内关系平均度大于子网A时，关系r2对网络没有影响。在图6（c）和（d）中，关系r2强度占比越小，网络鲁棒性越强;关系r1的曲线相重合，说明子网B网内关系平均度小于子网A时，关系r1对网络没有影响。

下层子网平均度大于上层子网时，上层子网关系强度占比越小网络鲁棒性越强，下层子网的网内关系对网络没有影响。反之，下层子网关系强度占比越小网络鲁棒性越强，上层子网的网内关系对网络没有影响。

2.4 加载关系平均度不同条件下网内关系和加载关系对网络的影响

与耦合网络不同，复合网络中存在多种关系，节点间存在关系强度，上述实验已经证明了关系强度比例参数对网络鲁棒性有着决定性影响。为了探究在加载关系平均度不同条件下关系强度对网络的影响，进行相应的实验。首先，构建节点总数为200，子网络A和B的拓扑结构为WS的复合网，参数α，β为1，两子网的网内关系平均度都设为2，加载关系平均度分别为2，4，6，8，当关系强度比例参数取不同值时，得出的S-λ曲线如图7所示。

加载关系平均度越大，网内关系r2和加载关系r3的曲线越相近，当加载关系平均度为8时，曲线最终重合，说明二者对网络的作用效果一致;除此之外，随着加载关系平均度的增大，加载关系对网络鲁棒性的提高程度随之减小，可以推断出加载关系强度足够大时，加载关系对网络没有影响。

3 结论

针对目前耦合网络级联失效的研究仅限于单个关系的问题，根据多子网复合复杂网络模型建立了复合网络模型，对多种关系和网络拓扑特征的相互影响进行了综合研究。研究表明：网络中两子网拓扑结构不同，网内关系对网络的影响不同;加载关系强度越大，网络鲁棒性越强，但随着加载关系平均度的增大，加载关系对网络的影响力随之减小;网内关系平均度比例不同，网内关系对网络的影响不同。因此为了有效保护现实中的网络系统，当遭到蓄意攻击和随机故障时，应当考虑节点间存在的多种关系类型，采取不同的方案，以达到最大程度降低损坏的目的。今后将两子网之间的加载关系从单向支持改为双向依赖，来进一步研究。

参考文献

[1]姜建秋，李军.一种基于SAM+的极简网络设计与实现[J].青岛大学学报（自然科学版），2018，31（3）：69-73.

[2]魏访.TD-LTE技术在智能电网无线通讯中的应用[J].青岛大学学报（自然科学版），2018，31（3）：128-132.

[3]房翠娟，邵峰晶，隋毅，等.基于复杂网络的气象网络分析[J].青岛大学学报（自然科学版）， 2017，30（4）：47-54.

[4]ROSATO V， ISSACHAROFF I， TIRITICCO F， et al. Modelling interdependent infrastructures using interacting dynamical models[J]. International Journal of Critical Infrastructure， 2008， 4（1-2）： 63-79.

[5]孫雅萍. 对中国南方特大雪灾的成因分析及思考[J]. 国土与自然资源研究，2009（2）： 72-73.

[6]GOH K I， HAHNG B， KIM D， et al. Fluctuation-driven dynamics of the Internet topology[J]. Physical Review Letters， 2002， 88（10）： 108701.

[7]BULDYREV S V， PARSHANI R， PAUL G， et al. Catastrophic cascade of failures in interdependent networks[J]. Nature， 2010， 464（7291）： 1025-1028.

[8]CHEN Z，DU W B，CAO X B，et al. Cascading failure of inter-dependent networks with different coupling preference under targetedattack[J].Chaos，Solitons and Fractals，2015，80（11） ： 7-12.

[9]李甍娜，郭进利.负荷作用下的相依网络鲁棒性研究[J].计算机应用研究， 2019， 36（8）：2388-2391.

[10] 陈世明，吕辉，徐青刚. 基于度的正/负相关相依网络模型及其鲁棒性研究[J].物理学报，2015，64 （4）：363-373.

[11] 杨程成，杨春.相互作用网络耦合关系对其鲁棒性的影响[J].西南大学学报，2015，37（9）：145-149.

[12] 陈世明，戴亚明，程运洪.提高相依网络鲁棒性的加边策略研究[J].电子科技大学学报，2019，48（1）：103-109.

[13] HUANGX Q， GAO J X， BULDYREV S V， et al. Robustness of interdependent networks under targeted attack[J].Physical Review E，2011，83（6）：778-804.

[14] LIU R R， JIA C X， ZHANG J I， et al. Robustness of interdependent networks under several intentional attack strategies[J]. Journal of University of Shanghai for Science and Technology， 2012， 34（3）： 235-239.

[15] 刘文静，靳岚，张金刚.负载作用下相互依存网络的鲁棒性分析[J].甘肃科学学报，2018，30（4）：115-118.

[16] 郭伟奇， 朱瑞晨， 孙璇. 考虑节点负载容量的相依网络鲁棒性研究[J]. 信息化研究， 2019， 285（4）：35-39.

[17] 张一帆， 顾仁涛. 基于节点和流关联的双层耦合网络鲁棒性分析[D].北京：北京邮电大学.2019.

[18] 张文萍. 基于耦合网络的级联失效研究[D].杭州：浙江大学. 2015.

[19] 徐红兵， 张维. 基于耦合策略的相依网络级联故障研究[J]. 井冈山大学学报（自然科学版）， 2018，39（5）：57-61.

[20] SHAO J， BULDYREV S V， HAVLIN S， et al. Cascade of failures in coupled network systems with multiple support-dependence relations [J]. Physical Review E， 2011， 83（3）： 036116.

[21] FU G H， DAWSON R， KHOURY M， et al. Interdependent networks： Vulnerability analysis and strategies to limit cascading failure[J]. European Physical Journal B， 2014， 87（7）： 148

[22] 陈世明，邹小群，吕辉，等.面向级联失效的相依网络鲁棒性研究[J].物理学报，2014，63（2）： 432-441.

[23] 彭兴钊，姚宏，杜军，等.负荷作用下相依网络中的级联故障[J].物理学报，2015，64（4）：355-362.

[24] ZHANG L， FU B B， LI S B， et al. Cascading failures coupled model of interdependent double layered public transit network[J]. International Journal of Modern Physics C， 2016，27（2）：1650145.

[25] JIA N， SUN G， CHEN C C， et al. Research on robustness of coupling networks based on multi-subnet composite complex network model[C]// 2nd IEEE Eurasia Conference on Biomedical Engineering， Healthcare and Sustainability （ECBIOS）. Tainan， 2020.

[26] 隋毅.多子网复合复杂网络模型及其相关性质和研究[D].青岛：青岛大学，2012.