基于多关系网络的边转移扩容策略

高峰 孙更新 宾晟

摘要：为缓解网络拥塞、提高网络容量，利用真实网络中节点间存在多种关系的特性，基于多子网复合复杂网络模型提出了一种适用于多关系网络的边转移扩容策略。通过改变网络的拓扑结构，删除高介数节点之间的边，同时，在最短路径较长的节点对之间添加边以此来达到扩大网络容量的目的。研究结果表明，边转移策略降低了网络中节点介数的最大值，有效地缩短了网络平均最短路径，均衡了节点之间的信息负载，最大化的提高了网络容量。

关键词：复杂网络;多子网复合复杂网络模型;扩容;网络容量;介数

中图分类号：TP393.0

文献标志码：A

文章編号：1006-1037（2021）03-0038-05

现实世界中的网络往往具有小世界[1]、无标度[2]等特征，研究人员基于上述特征建立复杂网络模型，通过对复杂网络模型上的信息传播特征及其本质属性的研究，为解决真实问题提供参考。近年来，随着交通网、互联网等网络规模的扩大，网络拥塞问题愈发严重，如何有效的缓解网络拥塞以及提高网络的传输性能成为研究热点。目前，针对上述问题的研究大致分为两种：研究网络动力学过程[3-5]，通过高效的信息传输策略来缓解网络的拥塞程度，典型的有最短路径策略[6-7]、动态路由策略[8]、度和最小路由策略等[9];研究网络的拓扑结构[10-12]，通过优化网络拓扑结构扩大网络的拓扑容量，延缓网络拥塞的发生，从而提高网络的传输性能。考虑到添加边的成本，学者们提出了删边扩容策略。比如，Liu等[13]提出了一种高度优先策略，关闭了部分大度节点之间的链路，从而提高网络容量。基于上述研究，Huang等[14]对删边扩容策略进行了优化，提出一种更有效的删边策略，删除部分与高介数节点相连的边，从而均衡各节点之间的负载。随着研究的深入，学者们发现在网络中适当加边的扩容效果更好，Huang等[15]提出一种基于最长最短路径添加边的策略。赵焱鑫等[16]考虑到介数对网络容量的影响，对上述加边策略进行了优化。上述研究都在传统网络中进行，真实网络中，节点之间大多存在多种关系，以交通网为例，两地之间存在着飞机、火车、轮船、汽车等多种运输方式。现实世界中，类似于交通网，个体之间存在着多种关系的网络可以描述为多关系网络[17]。已有研究与真实网络中的信息传输存在着较大的差异。本文针对真实网络中个体间存在多种关系的特点，基于多子网复合复杂网络模型，结合网络拓扑容量与节点最大介数成反比的结论，提出适用于多关系网络的边转移扩容策略。

1 网络模型

本文基于多子网复合复杂网络模型（简称复合网），定义了复合网上的网络流量模型。

1.1 多子网复合复杂网络模型

多子网复合复杂网络模型是一种能够描述个体间多种关系的新型网络模型[18]，该模型将复杂系统中个体间的相互关系映射为向量空间中的多维向量，定义了向量复合网，将组网运算转化为向量空间的基变化。为复杂系统的描述及其研究提供了新方法。

该模型将多子网复合复杂网络定义为一个四元组G=（V，E，R，F）：V={v1，v2，…，vm}，表示节点的集合，m=V是集合V的阶;E=<vh，vl>|vh，vl∈V，1≤h，l≤mV×V，表示节点间连边的集合;R=R1×…×Ri×…×Rn=（r1，…，ri，…，rn）|ri∈Ri，1≤i≤n，Ri表示节点间一种相互作用的集合，n是节点间相互作用关系的总数，R可以为空集;映射F：E→R。

1.2 流量模型

在复合网中，假设所有节点都可以产生、接受和传输信息，每个节点都有一个信息等待队列，用以保存等待处理的信息，容量为C，任意两节点之间存在多种关系，信息随机选择任意关系进行传输，不同关系的信息处理能力不同，例如，节点间的某关系ri的处理能力为p，即在每个时间步内，节点vh（vh∈V）通过关系ri最多向其邻居节点传输p条信息。节点可以同时通过多种关系向其邻居节点传输信息。在每个时间步内，系统中产生R条信息，信息的源节点和目的节点在复合网中随机选择，并且，源节点与目的节点不重合。当信息到达其目的节点后从系统中删除。

2 边转移扩容算法

不同于传统网络，复合网节点间存在多种关系，因此，对于任意源节点s与目的节点t之间的传输路径l定义为

其中，sri表示信息通过关系ri将信息传输给其邻居节点，vm是此路径上的第m个中间节点。

根据复合网中的传输路径，复合网中节点在最短路径策略下介数为

其中，σst表示节点s和t之间的最短路径条数，σst（v） 表示其中经过节点v的最短路径数目，经过相同节点，但是传输所用的关系不同，则其路径不同。σst（v）越大，则有更多的最短路径经过节点v，所以节点v发生拥塞的概率越大。

由于每一个时间步复合网络中都会产生R个信息，此时规模为N的网络中的某个节点v需要处理信息的平均数量约为

从〈θ〉可知，网络中介数最大的节点最早发生拥塞。将网络中节点的最大介数数表示为g，则

网络中负载系数最大的节点信息数量超出其信息容量C时，网络发生拥塞。所以网络发生拥塞的临界值为

即为当前复合网的网络容量Rc。

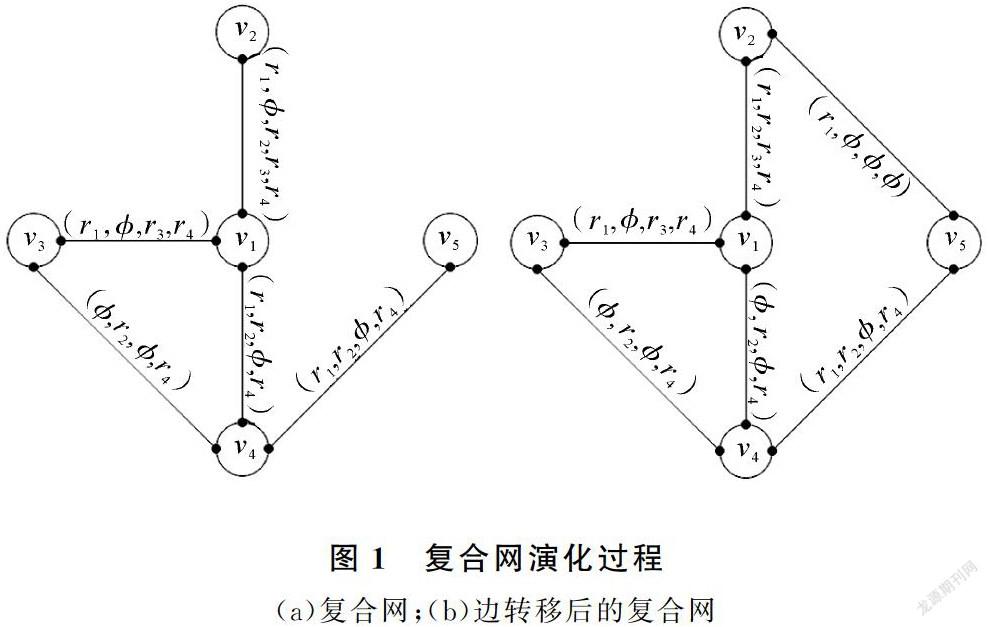
从复合网网络容量的定义中不难得出，网络容量Rc与节点的介数呈反比，即降低网络的最大介数，即可增大网络容量。由此得出网络演化过程，如图1所示。

对于网络图1 （a），不难得出节点v1介数最大，则其网络容量取决于v1，gv1的值越大，网络容量越小。在v1的邻居节点中v4的介数较大，删除v1和v4之间信息处理能力最小的关系r1，对节点v1和v4的影响最小，但gv1的值变小，网络容量得到提高。在最短路径最长的节点对v2和v5之间添加ri关系，得到网络图1 （b）。此时，缩短了网络中的平均路径长度，相比网络图1 （a），网络图1 （b）的信息处理能力更优秀。

基于上述演化過程，提出边转移扩容策略。首先，删除与高介数节点与其邻居节点中介数最大的节点之间的信息处理能力最小的关系ri;其次，将删除的关系添加到最短路径最长的两节点之间（该算法默认所有节点可达）。具体步骤如下：

Step 1 计算网络中所有节点的介数存于矩阵Q，计算网络中任意未直接相连的两节点之间的最短路径，存于矩阵P;

Step 2 在矩阵Q中寻找介数最大的节点，并寻找其邻居节点中介数最大的节点，删除两节点之间信息处理能力最小的边ri，若该节点对之间只存在一种关系，则删除其他符合条件的关系。在矩阵P中寻找最长的最短路径，并将其节点对存入集合E;

Step 3 在E中寻找介数最小的节点对（u，v），并在（u，v）之间添加ri;

Step 4 重复上述过程，直到转移边的数目达到f。

在该算法中，计算最短路径时用到了Dijkstra算法。该算法的实质是删除大介数节点之间的连边，使得最大介数减小，从而使网络容量增大。同时，将删除的边加入到最短路径最长的节点对之间，从而降低了平均传输路径，提升了整个网络的信息处理能力。通过边的转移，在不增加整体网络资源的情况下，最大化地提高网络容量。

3 实验结果及分析

在实验中，针对网络容量Rc、平均最短路径Lav和节点的介数3个指标，将本文策略（记为TS）和最低度添加边策略（LS）与最长最短路径添加边策略（DS）进行比较。复合网规模设置为N=1 000，节点间最大关系数为4，关系的信息处理能力分别为1、2、3、4（即每个时间步内，节点v只能通过某关系i向其邻居节点传输1、2、3、4条信息），节点的信息容量C=10。在最短路径传输策略下，对3种扩容策略进行10次实验，取其平均值。

图2是3种策略对平均路径长度Lav的影响，可知，TS和DS对减少节点间路径长度的效果比LS好，并且在改变边的数量f（TS策略中转移边的数量，DS、LS策略中添加边的数量）较少时，TS与DS的效果相差不多，在改变边的数量较多时，DS的效果更加显著。图3是网络的拓扑容量与f之间的关系，随着f的增加，上述3种策略都可以提高网络容量。相比之下，TS策略对于网络性能的提升更加显著。DS策略虽然在减小平均路径上的表现比TS更好，但是随着f的增加，网络中各节点的介数也在不断的增大。但是TS策略，在减小平均路径的同时，网络中节点的介数也在降低，由此可以体现TS策略的优越性。

对比3张图可以发现，相比于TS，DS和LS策略下网络中节点的介数相差较大，这使得信息在网络中传输的时候网络中各节点之间的信息负载不均衡，低介数节点的利用率不高，高介数节点较早的出现拥塞现象。而TS策略下，网络中节点的介数相差较小，网络中各节点之间的信息负载比较均衡，低介数节点的利用率较高，延缓了拥塞现象发生的时间，从而提高了整个网络的信息处理能力。

通过上述仿真实验可以发现，虽然在改变边数量较大时，在缩短最短路径长度的效果上，本文策略不如最长最短路径添加边策略，但是边转移策略与最低度添加边策略和最长最短路径添加边策略相比，在网络整体的性能提升上的表现更加优秀。边转移策略不仅能够有效地缩短最短路径，并且可以均衡各节点之间的信息负载，较大程度地提高网络容量。

4 结论

本文提出了一种基于多关系网络的边转移扩容策略，删除高介数节点对之间的边，同时在最短路径较长的节点的节点对之间添加边，以此来降低网络中节点的介数，同时缩短最短路径长度。并在多子网复合复杂网络模型上进行仿真实验，对网络中节点的介数、平均最短路径长度和网络容量进行了分析，与其他扩容策略相比，本文提出的策略能够更好地提高网络性能，对提高真实网络的网络性能提供了参考。

参考文献

[1]WATTS D， STROGATZ S. Collective dynamics of 'small-world networks[J]. Nature，1998，393（6684）：440-442.

[2]BARABASI A， BONABEAU E. Scale-free networks[J]. Scientific American. 2003， 288（5）：60-69.

[3]ZAGER L， VERGHESE G. Epidemic thresholds for infection in uncertain networks[J]. Complexity， 2009， 14（4）：12-25.

[4]TNJES R， MASUDA N， KORI H. Synchronization transition of identical phase oscillators in a directed small-world network[J]. Chaos. 2010， 20（3）：033108. doi： 10.1063/1.3476316. PMID： 20887048.

[5]LEYVA I， NAVAS A， SENDIA-NADAL I， et al. Synchronization waves in geometric networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics， 2011， 84（6 Pt 2）：065101.

[6]GOH K I， KAHNG B， KIM D. Universal behavior of load distribution in scale-free networks[J]. PhRvL， 2001， 87（27）：278701.

[7]ZHAO L， LAI Y C， PARK K， et al. Onset of traffic congestion in complex networks[J]. Physical Review E， 2005， 71（2）：026125.

[8]万琳， 范秋灵， 胡海荣. 复杂网络路由策略优化设计[J]. 兵器装备工程学报， 2013， 34（11）：103-105.

[9]TANG M， ZHOU T. Efficient routing strategies in scale-free networks with limited bandwidth[J]. Physical Review E， 2011， 84（2）：026116.

[10] WU J， BARAHONA M， TAN Y J， et al. Natural connectivity of complex networks[J]. Chinese Physics Letters， 2010， 27（7）：078902.

[11] 邵志刚. 人体心律动力学的网络分析[J]. 应用物理学快报，2010，96（7）：4972.

[12] TODA A A. Income dynamics with a stationary double pareto distribution[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics， 2011， 83（4）：046122.

[13] LIU Z， HU M B， JIANG R， et al. Method to enhance traffic capacity for scale-free networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics， 2007， 76（3）：037101.

[14] HUANG W， CHOW T W S. An efficient strategy for enhancing traffic capacity by removing links in scale-free networks[J]. Journal of Statistical Mechanics Theory and Experiment， 2010， 2010（1）：P01016.

[15] HUANG W， CHOW T W S. Effective strategy of adding nodes and links for maximizing the traffic capacity of scale-free network[J]. Chaos An Interdisciplinary Journal of Nonlinear Science， 2010， 20（3）：509.

[16] 赵焱鑫， 李黎， 王小明. 复杂网络加边扩容策略研究[J]. 计算机应用研究， 2015， 32（6）：1839-1841.

[17] BERLINGERIO M， COSCIA M， GIANNOTTI F， et al. Multidimensional networks： foundations of structural analysis[J]. World Wide Web-internet & Web Information Systems， 2013， 16（5-6）：567-593.

[18] 隋毅. 多子網复合复杂网络模型及其相关性质的研究[D]. 青岛：青岛大学， 2012.