考虑夹头与刀具过渡段的主轴系统精确建模

朱坚民,石园园,田丰庆,黄扬辉,孟 聪,陈 琳

(上海理工大学 机械工程学院，上海 200093)

0 引言

主轴系统刀尖点频响函数是评价铣床加工系统动态特性的主要依据，也是优选铣削工艺参数的重要指标[1-2],主轴系统动力学模型的准确性直接关系到机床刀尖点频响函数的预测精度，其因包含较多的组成部件和结合面而在很大程度上增加了动力学建模和分析的难度，因此建立能够确切地模拟机械结构动力特性的动力学模型并准确辨识结合面动力学参数具有重要的意义[3]。

目前，响应耦合子结构法(Receptance Coupling Substructure Analysis, RCSA)以原理简单、实验便捷的特点，已经成为主轴系统建模的主要方法[4-5]，对该方法的研究主要集中在主轴—刀柄系统精确建模与刀具精确建模两方面。SCHMITZ等[6-7]和MOVAHHEDY等[8]将机床的主轴系统分为主轴刀柄和刀具两个子结构，模型中只考虑刀柄—刀具结合面，其他结合面视为固接,分别采用最小二乘法和遗传算法(Genetic Algorithm, GA)辨识刀柄—刀具结合面参数；王二化等[9]兼顾主轴—刀柄、刀柄—刀具两个结合面，针对主轴系统的影响建立主轴系统模型，并采用粒子群算法辨识了结合面参数；朱坚民等[10]考虑机床主轴—刀柄、刀柄—部分刀具、部分刀具—剩余刀具3个结合面的影响，采用GA辨识结合面参数，进一步提升了刀尖点频响函数(Frequency Response Function,FRF)的预测精度。以上文献均考虑结合面因素建立了主轴系统等效动力学模型，不同程度地提升了建模精度，文献[11-12]还表明主轴—刀柄结合面的刚度参数通常高于其他结合面两个数量级，对刀尖点FRF的影响更大，而且实验数据的真实性受外部因素影响大，因此本文将主轴—刀柄结合面视为固结。然而，以上文献均未考虑刀柄中弹性夹头对刀尖点FRF的影响，弹性夹头是刀柄中的弹性部件，对刀具装夹至关重要，其自身的动态性能对主轴系统是动态特性影响较大，不可忽视[13]。

刀具精确建模方面的难点是刀齿部分外形复杂，等效直径难求。最初的模型没有考虑刀齿的影响，直接将刀齿最外端的包络圆直径作为刀具的等效直径[14-15]，因此计算误差较大，预测精度较低；KOPS等[16]和MANCISIDOR等[17]分别采用等刚度法和改进的等惯性矩法计算了3齿和4齿铣刀刀齿的等效直径，提升了刀具的建模精度；朱坚民等[18]采用GA，通过寻优确定刀齿的等效直径，该方法精度较高但过程相对繁琐，而且每次更换刀具需要重新实验、重新优化；ZHANG等[19]采用等平均惯性矩法计算了刀齿的等效直径，该方法的计算结果精度达到2.7%，而且方法相对简单；朱坚民等[10]等采用解析法建模将铣刀分成十多段进行精确建模，结果表明刀柄—刀齿过渡段不能简单地等同为刀齿，需要单独考虑，该方法的计算过程比较复杂，不利于实际应用。

针对上述问题，本文以VMC850E型立式加工中心主轴系统为研究对象，提出考虑主轴刀柄—夹头、夹头—刀具两个结合面，基于RCSA法建立主轴系统精确动力学模型，采用布谷鸟搜索(Cuckoo Search, CS)优化算法对结合面进行参数辨识，并利用等平均惯性矩法对铣刀刀齿和过渡段进行精确建模，以获得较高的预测精度。

1 主轴系统的精确建模

机床主轴系统主要包括主轴、刀柄、刀具夹头和刀具等，刀尖点的频响函数可以准确反映机床加工系统在刀尖点位置的动态特性，为准确预测刀尖点频响函数，避免机床处于共振频率区域而产生切削振颤，本文对现有机床主轴系统模型的建立方法进行改进，考虑到刀柄锥部为标准尺寸，其在加工过程中会受到较大的夹紧力，可以将刀柄锥部与机床主轴视为一体，因此本文以VMC850E立式加工中心为例，将机床主轴系统划分为机床—主轴—刀柄、刀具夹头、刀具3个子结构，在各自结构之间建立弹簧阻尼单元，各子结构的划分情况及坐标点定义如图1所示。

图1中，刀具为子结构Ⅰ，刀具夹头为子结构Ⅱ，机床—主轴—刀柄为子结构Ⅲ；a1，a2表示刀具两端的坐标，b1，b2表示刀具夹头两端的坐标，c表示刀柄末端坐标点。可用K1，K2分别表示刀具—夹头结合面的复刚度矩阵与主轴刀柄—夹头结合面的复刚度矩阵，

(1)

式中：k1，c1分别表示刀具夹头—刀具结合面受力载荷作用的平动刚度和平动阻尼；k2，c2分别表示刀具夹头—刀具结合面受力矩作用的平动刚度和平动阻尼；k3，c3分别表示刀柄—刀具夹头结合面受力载荷作用的平动刚度和平动阻尼；k4，c4分别表示刀柄—刀具夹头结合面受力矩作用的平动刚度和平动阻尼；w为角频率。

子结构Ⅰ和子结构Ⅱ的频响函数与位移及外力的关系分别为：

(2)

(3)

式中：x为结构的位移矢量；F为力矢量；H为频响函数。假设夹头—刀具结合面处的受力幅值相同，方向相反，则由频响函数的定义可知，夹头—刀具结合面由内力产生的位移如式(5)所示，其中pi为结合面的刚度阻尼矩阵，i为虚数单位。

(4)

(5)

由式(2)～式(5)可得子结构Ⅰ和子结构Ⅱ的频响函数与位移及外力的关系为：

(6)

(7)

因此夹头—刀具整体结构的位移和外力之间的关系可表示为

(8)

同理，将子结构Ⅰ与子结构Ⅱ耦合后的结构作为一个新的子结构Ⅰ-Ⅱ，将子结构Ⅲ与Ⅰ-Ⅱ耦合可得刀尖点的原点频响函数矩阵。刀柄末端频响函数与位移及外力的关系为

(9)

根据力平衡与位移协调方程，刀柄—夹头—刀具整体结构的位移和外力之间的关系可表示为

(10)

(11)

(12)

2 各子结构频响函数矩阵计算

2.1 主轴刀柄末端频响函数计算

刀柄部分结构复杂且处于非自由状态，难以用理论方法直接计算其端点频响函数矩阵Scc，Scc可表示为

(13)

式中：hcc为刀柄末端频响函数矩阵中的位移频响函数，可以利用模态锤击实验直接获得；主轴刀柄部分的端点频响函数矩阵lcc，ncc，pcc中包含转动频响函数，很难通过模态锤击实验直接获得。

目前求解处于非自由状态下的子结构转动频响方法主要为有限差分法、多段EB(Euler-Bernoulli)梁优化法和方程求解法等。有限差分法是一种理论与实验相结合的方法，其计算简单，实验方便，精度高，因此本文采用有限差分法获得主轴—刀柄末端频响函数。在主轴系统中，为保证加工的可靠性及加工精度，刀柄会受到螺母夹紧力的作用，因此实验时可将刀柄与螺母视为一体，所建立的模型如图2所示。

图中，在A，B两处安装加速度传感器，对其分别施加激振力，获得A点的原点位移频响函数hAA和A点到B点处的跨点位移频响函数hAB。由频响函数的互易性原理可知，nAA=lAA，根据式(14)和式(15)可得主轴刀柄端点处的转动频响函数nAA和pAA，式(16)为刀柄末端频响函数矩阵。

(14)

(15)

(16)

式中g为两个传感器之间的距离，由式(14)可知转动频响函数nAA的计算精度取决于实验获得的主轴刀柄端点A处的移频响函数hAA与A，B两点跨点位移频响函数hAB之间的差值，因此A，B两点之间的距离g应尽可能地大。本文根据刀柄的实际结构，在模态锤击实验中令g=8 cm，为进一步保证所得实验数据的精度，多次测量hAA，hAB取其平均值，以降低实验误差，提高计算精度。

2.2 刀具夹头的精确建模及频响函数计算

刀具夹头体积较小且结构复杂，模态锤击实验因其局限性不易获得夹头两端的频响函数，而难以建立精确的动力学模型，本文根据夹头的结构特点对夹头模型进行适当简化，将其等效为多段等直径阶梯圆柱梁模型(如图3)，各段等直径圆柱梁两端的频响函数矩阵可由Timoshenko梁理论计算得到，然后采用RCSA法对刀具夹头等效模型中的各小段进行刚性耦合，计算得到夹头整体的频响函数矩阵。

转动惯量是反映刚体转动特性的一个重要物理量，为确定刀具夹头两端圆锥台的等效直径，本文采用等转动惯量法对夹头进行等效。均质圆柱对母线的转动惯量

(17)

式中：R1为圆柱的半径，m1为质量。均质圆锥对母线的转动惯量

(18)

式中：R2为圆锥的底面半径；h2为高；m2为质量。

圆台可以看作为同一顶点大小圆锥之差，若圆台高为h，质量为m，上底面半径为r，下底面半径为R，总高为H(如图4)，则圆台的转动惯量。

(19)

由转动惯量相等可知，圆锥的等效直径

(20)

为验证该等效模型的正确性，本文将有限元分析的夹头固有频率与RCSA分析出的夹头固有频率进行对比，结果如表1所示。可见，本文所建夹头等效模型是可行、正确的。

表1 自由状态下刀具夹头的固有频率

2.3 铣刀的精确建模及频响函数的计算

整体式立铣刀一般由刀齿和刀杆两部分构成，其中刀齿过渡段是区分不同铣刀的重要部分，也是影响实际加工的重要因素，由于刀齿结构模型复杂，目前众多学者根据不同的等效原则将铣刀的刀齿段等效为均匀等直径圆柱梁，忽略了铣刀刀齿和刀柄间存在过渡段的事实。表2所示为不同刃数立铣刀各段的截面形状，通过分析可知，不同刃数铣刀的截面形状不一样，将刀齿直接等效为均匀等直径圆柱梁不符合实际情况，因此本文根据2刃、3刃、4刃铣刀截面的实际形状建立铣刀截面数学模型。

表2 立铣刀刀齿截面形状

等平均惯性矩法将直齿圆柱齿轮等效为均匀等截面圆柱梁时所得的固有频率误差最小[20]，因此本文采用该方法对铣刀模型进行等效。首先将整体式立铣刀划分为刀杆、刀齿与刀杆的过渡段、刀齿3个子结构，分别对应子结构Ⅰ、子结构Ⅱ和子结构Ⅲ，如图5所示。各子结构等直径圆柱梁两端的频响函数矩阵由Timoshenko梁理论计算得到，采用RCSA法对刀具等效模型中的各小段进行刚性耦合，计算得到刀具频响函数矩阵。

2.3.1 铣刀刀齿截面惯性矩的计算

由表2可知，铣刀各子结构的截面形状均可由三角形、扇形、半圆等基本图形构成，因此可以先分别计算截面中单个三角形区域和扇形区域对x轴的惯性矩和对y轴的惯性矩，再根据平行轴定理和转轴定理得到剩余部分三角形区域和扇形区域的截面惯性矩，将各部分叠加得到2刃、3刃、4刃铣刀过渡段截面对x轴的总惯性矩和对y轴的总惯性矩。将1/2的2刃铣刀截面划分为2个区域(如图6)，可以看出该截面由半圆i(i=1，2)组成，分别计算i区域对xi轴和yi轴的惯性矩，通过平行移轴定理叠加计算得该截面对x轴和y轴的惯性矩。因此2刃铣刀刀齿截面对x轴和y轴的总惯性矩为：

(21)

(22)

将3刃铣刀的1/3截面划分为4个区域(如图7)，可以看出该截面由半圆、扇形和三角形构成，分别对i(i=1，2，3，4)区域建立坐标xi，yi，计算i区域对xi轴和yi轴的惯性矩，根据平行移轴和转轴定理，通过各区域叠加计算出该截面对x轴和y轴的惯性矩

(23)

式中：

(24)

(25)

(26)

(27)

(28)

将4刃铣刀的1/4截面划分为4个区域(如图8)，可以看出该截面由半圆、扇形和三角形构成，分别对i(i=1，2，3，4)区域建立坐标xi，yi，计算i区域对xi轴和yi轴的惯性矩，根据平行移轴定理，通过各区域叠加计算出该截面对x轴和y轴的惯性矩

(29)

式中：

(30)

(31)

(32)

(33)

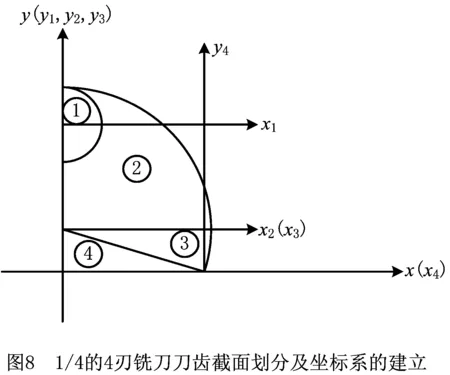
由式(29)～式(33)可得4刃铣刀刀齿截面对x轴和y轴的总惯性矩：

(34)

(35)

2.3.2 铣刀过渡段截面平均惯性矩的计算

2刃铣刀过渡段截面对x轴和y轴的总惯性矩为:

(36)

3刃铣刀过渡段截面对x轴和y轴的总惯性矩为：

(37)

4刃铣刀过渡段截面对x轴和y轴的总惯性矩为：

(38)

2.3.3 铣刀刀杆截面惯性矩的计算

铣刀刀柄部分截面为圆形，因此该截面对x轴和y轴的惯性矩为

(39)

由式(21)～式(39)可得不同刃数铣刀的截面惯性矩，再由式(40)得到2刃、3刃、4刃不同型号铣刀各子结构的等效直径

(40)

为验证该等效模型的正确性，本文将模态锤击实验所得的刀具第三阶固有频率实验值与RCSA分析出的刀具固有频率理论值进行对比，结果如表3所示。其中刀具1～6为2刃铣刀，刀具7～9为3刃铣刀，刀具10～14为4刃铣刀。由表3可知，本文所建刀具等效模型是可行、正确的。

表3 自由状态下刀具的固有频率

3 结合面参数辨识

3.1 结合面动力学参数的灵敏度分析

理论上，通过计算式(10)可准确辨识出刀柄—夹头—刀具之间两个结合面的等效频响函数矩阵，但由于模态锤击试验所获得的测量数据中不可避免地包含噪声信号，该信号在理论运算过程中被放大，使辨识结果出现不适定问题。为了避免不适定问题，使辨识结果能够真实反映刀柄—夹头、夹头—刀具两个结合面的动态特性，本文提出采用灵敏度的方法选取对结合面参数变化特别灵敏的频响函数所对应的固有频率来辨识两个结合面的动力学参数。

首先设定各等效参数的初始范围，采用分层抽样的方法确定n组刚度阻尼参数样本点，使其在采样空间均匀分布。通过这些样本点确定不同结合面等效刚度及等效阻尼参数，可获得不同参数下的刀尖点频响函数和模态振型；采用灵敏度分析方法选取对结合面参数变化特别灵敏的频响函数所对应的固有频率来辨识刀柄—夹头、夹头—刀具两个结合面的动力学参数；获得归一化频率与刀柄—夹头、夹头—刀具两个结合面的接触刚度和接触阻尼的关系，从而确定两个结合面各等效刚度与等效阻尼参数的灵敏区间。

3.2 结合面动力学参数的辨识方法

本文采用CS优化算法对结合面参数进行辨识。CS算法是杨新社等[20]于2009年提出的一种启发式智能优化算法，而且通过标准测试函数和随机测试函数进行大量对比实验表明，该算法获取的最优解远优于粒子群优化算法和GA。CS算法具有简单易理解，在解决特殊问题时无需重新匹配大量参数等优点，其寻优过程分为两个阶段：①粗搜索，利用混沌变量的遍历性进行粗搜索，具体是采用Logistic方程产生混沌序列，确定次优化值；②细搜索，以次优化值为中心，将高斯分布作为此处附加的微小扰动进行小幅度变化来确定最优解。通过分析各结合面刚度阻尼参数的灵敏度获得各等效参数的灵敏范围，以刀尖点频响函数实验值SHTa1a1s与理论值SHTa1a1的误差值最小为目标函数，即

(41)

结合面的刚度和阻尼参数为寻优变量，通过CS算法迭代循环确定刀柄—夹头、夹头—刀具两个结合面的动力学参数，结合面等效参数辨识流程如图9所示。

CS寻优的初始参数设置为：粗搜索搜索次数为100，混沌序列长度为400，收敛值为0.000 051，细搜索次数为6，细搜索收敛值为0.000 053。

4 实验研究

4.1 刀柄末端频响函数实验

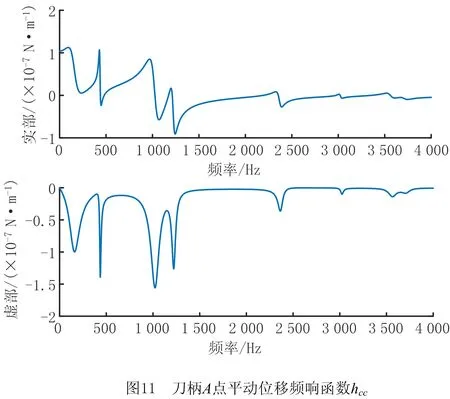
本文以VMC850E立式加工中心主轴系统为研究对象，如图10所示，在A，B两点安装BK 4525B型三向加速度传感器，用中型激振力锤在这两点的对立面施加激振力，通过LMS SCACAS Mobile205数据采集系统采集数据，采用LMS Test.Lab分析软件确定各刀柄末端位移频响函数的实测值。为了保证实验精度，进行5组实验，每组采集5次数据，由此获得刀柄A，B原点位移频响函数hAA和跨点位移频响函数hAB，如图11所示。同时采用有限差分法(即式(9))获得刀柄末端的转动频响函数，如图12和图13所示，由Maxwell的互异性可知nAA=lAA。

4.2 刀尖点频响函数实验

以2刃整体式立式铣刀为研究对象，将其安装在VMC850E立式加工中心上，将BK 4525B型三向加速度传感器安装在刀具末端，如图14所示，用激振力锤在C点的对立面施加激振力，通过LMS SCACAS Mobile205数据采集系统采集数据，采用LMS Test.Lab分析软件确定各铣刀刀尖点频响函数的实测值SHTa1a1s，经过分析得到各阶固有频率。

4.3 结合面参数辨识结果

通过实验分析刀尖点频响函数的第三阶固有频率对结合面参数的变化最敏感，故对主轴刀柄—夹头—刀具结合面的等效参数与刀尖点频响函数的第三阶固有频率进行灵敏度分析，可得归一化频率与刀柄—夹头—刀具结合面等效刚度和等效阻尼的关系，k1的辨识结果在5×105～1.0×107N/m之间，c1的辨识结果在150～350 N·s/m之间，k2的辨识结果在5.0×103～5.0×104N/m之间，c2的辨识结果在50～100 N·s/m之间，k3的辨识结果在1.0×106～1.0×108N/m之间，c3的辨识结果在80～180 N·s/m之间，k4的辨识结果在1.0×104～5.0×106N/m之间，c4的辨识结果在35～350 N·s/m之间。

通过第3章的结合面参数辨识原理可得2刃铣刀对应的刀柄—夹头—刀具结合面的等效刚度与阻尼参数，为验证本文辨识方法的可行性和可信度，通过对比GA和CS算法辨识结合面的效果(如图15)，可知CS算法的收敛性能优于GA。通过GA算法和CS算法预测的刀尖点频响函数理论值与实测值的对比如图16所示。CS算法对刀柄—夹头—刀具结合面等效参数的辨识结果如表4所示，对刀尖点频响函数前三阶固有频率实测值与预测理论值的对比结果如表5所示。

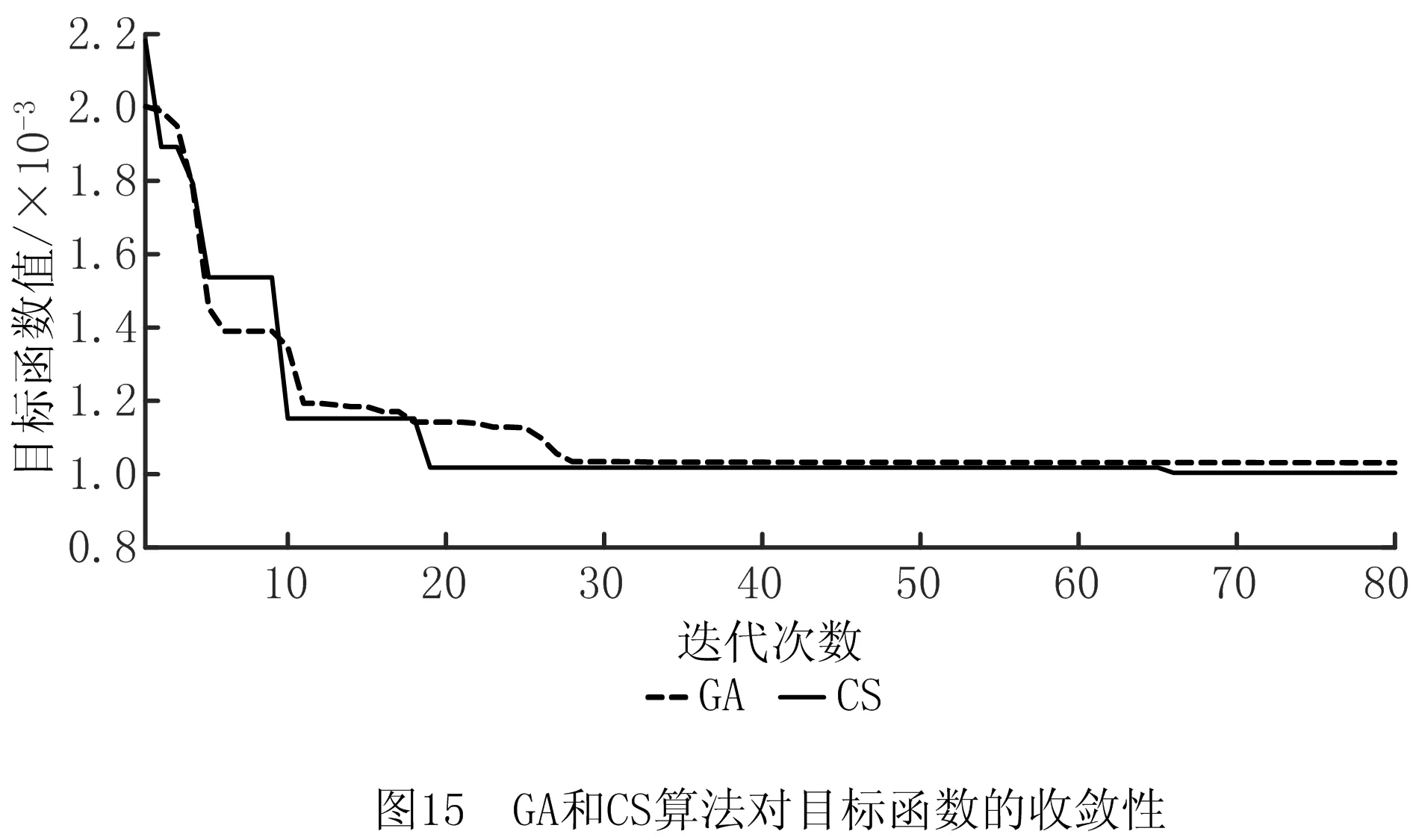
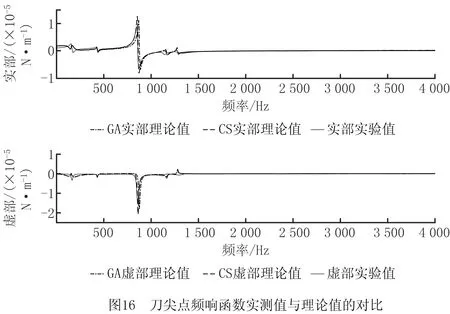
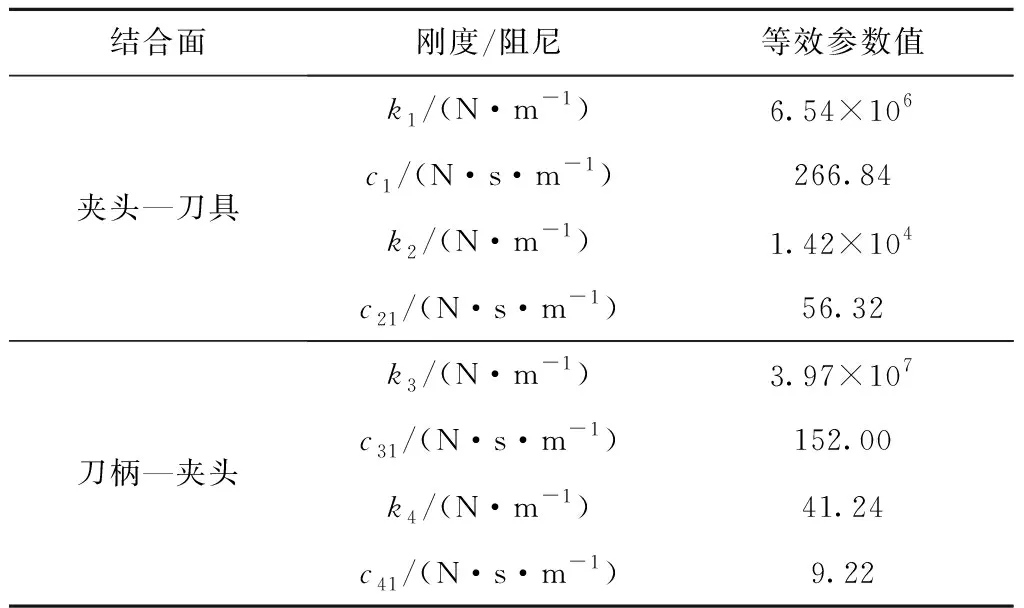
表4 刀柄—夹头—刀具结合面的等效刚度与阻尼参数

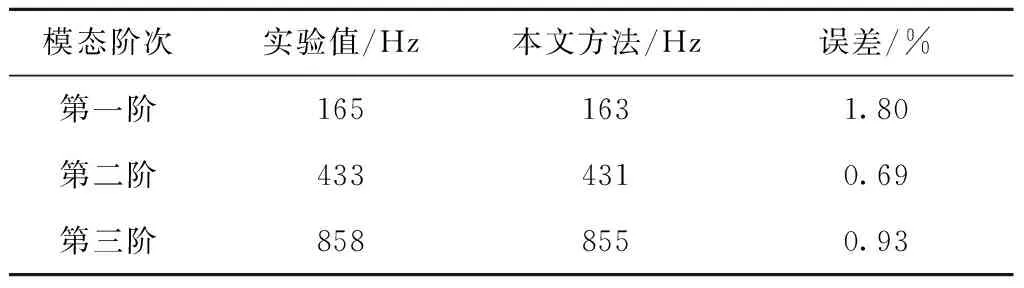
表5 刀尖点频响函数前三阶固有频率实测值与理论值的对比

由表5可知，通过本文方法对主轴刀柄—夹头—刀具结合面的刚度、组尼参数进行辨识，并根据辨识出的结合面等效参数预测刀尖点频响函数的前三阶固有频率，第三阶预测值与实测值之间的误差为0.93%，可见本文结合面参数辨识方法精度较高，具有可行性与正确性。

5 结束语

本文采用等转动惯量法对夹头进行精确建模，采用等平均惯性矩法对铣刀刀齿和过渡段的直径进行模型等效，然后基于RCSA法建立了主轴系统刀柄—夹头—刀具结合面等效模型，以刀尖点频响函数实验值与理论值误差最小为目标函数，采用CS算法辨识各结合面等效参数，并根据该参数预测出刀尖点频响函数的固有频率。由预测结果可知，第三阶固有频率的理论值与实测值之间的误差为0.93%，表明本文结合面参数辨识方法的精度较高，而且主轴系统结合面等效模型具有可行性和有效性。