双深度多层穿梭车仓储系统并行作业及建模分析
2021-09-13占翔南徐立云李爱平
占翔南,徐立云+,宓 宏,李爱平
(1.同济大学 机械与能源工程学院,上海 201804;2.浙江衢州联州致冷剂有限公司,浙江 衢州 324004)
0 引言
双深度多层穿梭车系统是近年来出现的一种新型智能立体仓库,依靠穿梭车完成水平作业,借助提升机完成垂直作业,从而实现货物的出入库作业,弥补了多层穿梭车系统中每个巷道只能由独立的穿梭车进行服务以及存储能力不足等缺点。然而,该系统也存在倒货作业和系统响应时间长等现象,如何提高双深度多层穿梭系统的作业效率是亟待解决的问题。
目前,国内外学者对立体仓库的研究多以多层穿梭车系统为研究对象,主要研究方法包括确定性模型分析法和排队模型分析法。确定性模型分析法可以根据作业顺序准确计算单次任务的作业时间,MALMBORG[1]首次对多层穿梭车系统展开研究,采用连续Markov链的方法来计算系统的水平作业和垂直作业时间,以评估系统的响应时间;WANG等[2]针对自动小车存取系统(Autonomous Vehicle Storage/Retrieval System,AVS/RS)建立了作业时间序列优化模型,并将系统的调度问题转化为装配线并行作业问题,通过优化任务队列减少穿梭车和提升机的等待时间来提高系统运行效率;杨玮等[3]针对双载式多层穿梭车仓储系统复合作业路径优化问题建立了作业时序数学模型,并采用混合植物繁殖算法进行求解与分析。排队模型分析法考虑了排队对系统性能的影响,可以更加准确地分析系统的性能指标,KUO等[4]将穿梭车服务流程和提升机服务流程分别建模为M/G/V队列和G/G/L队列,用于研究系统中的随机存储策略和结束点停留策略;ROY等[5]通过建立多层排队网络模型,并采用基于嵌入式Markov链的方法分析系统响应时间和资源利用率;CAI等[6]建立了多级半开环排队网络模型,并采用矩阵几何法分析了AVS/RS系统的利用率和输出效率,说明虚拟同步策略比物理同步策略更优。
然而,上述文献在建模过程中均采用了顺序作业方式,由于顺序作业方式下穿梭车和提升机之间的等待时间会增加系统响应时间,为进一步减小系统响应时间,HU等[7]首次对并行作业方式进行研究,并采用确定性模型对分体式自动存储系统(Split-Platform Autonomous Storage/Retrieval System, SP-AS/RS)的性能进行了分析,结果表明并行作业方式可以减小垂直平台和水平平台之间的等待时间;ZOU等[8]采用并行作业方式对AVS/RS系统进行分析,针对单个巷道建立了fork-join排队网络模型,比较了AVS/RS系统在并行作业方式和顺序作业方式下的系统性能。以上研究表明,并行作业方式可以减小系统响应时间,提高作业效率。对于双深度多层穿梭车系统,XU等[9]在顺序作业方式下对双深度多巷道存取系统建立了行程时间模型,分析了货位占用率对系统输出的影响,并给出了存在最佳货位占用率的条件;LERHER[10]在顺序作业方式下,对双深度多层穿梭车系统在单命令周期和双命令周期下进行了行程时间建模,但迄今为止,对双深度多层穿梭车系统并行作业及建模分析尚未进行研究。
综上所述,已有学者从多层穿梭车仓储系统及其相关问题出发,对仓储系统进行建模研究,并应用于工程优化问题,如仓储系统作业效率优化问题、作业任务调度问题等,但仍存在以下不足:①作业效率优化问题中多以顺序作业方式为研究基础,缺乏对并行作业方式的研究和优化,从而影响仓储系统的柔性;②针对单个巷道进行建模分析,并根据单个巷道的结果对仓储系统整体进行评估,缺乏对仓储系统整体的分析,若系统中出现跨巷道取货作业,该方法则不能准确评估系统性能指标;③缺乏对倒货作业的考虑,影响评估结果;④作业效率优化问题中,直接根据系统模型建立仿真模型进行验证,需要的时间较长且缺乏理论基础。
针对以上问题,本文以双深度多层穿梭车仓储系统为对象,考虑并行作业方式对作业效率的影响,先建立分离—聚合排队网络模型,然后考虑倒货作业时间和取货时间服从一般分布的特点,设计基于Coxian分布的近似分解算法进行求解。与根据单一巷道评估系统整体的方法相比,对仓储系统整体进行建模分析能够更准确地评估系统性能指标;另外,与仿真验证相比,该方法能够更快地评估系统性能指标且具有理论可行性。
1 问题描述
仓储系统建模是根据仓储系统配置和设备运行特点构建仓储逻辑系统来描述真实仓储系统[11]。仓储系统建模问题的关键在于:①如何根据系统配置和运行特点准确地描述仓储系统;②如何确定评价指标以保证模型的准确性和可靠性;③如何高效快速地对模型进行求解。同时,仓储系统建模是研究作业效率优化问题的基础,能够进一步为仓储系统作业调度和路径规划等问题提供指导。
目前,仓储系统的评价指标主要包括地面面积利用率、系统吞吐能力、系统响应时间和设备利用率等,而双深度多层穿梭车仓储系统因具备空间利用率高、系统吞吐能力强、设备利用率高等优点而受到众多企业的青睐。本文研究并行作业方式对双深度多层穿梭车仓储系统作业效率的影响,将系统响应时间、穿梭车和提升机利用率、平均等待时间和平均等待队长作为性能评价指标。系统响应时间指单个取货任务的完成时间,能够评估系统在不同配置和取货任务到达率下的吞吐量;穿梭车和提升机利用率用于评估系统设备的使用率,并可以据此找出系统瓶颈;平均等待时间和平均等待队长用来评估取货任务在系统外部的等待情况,可以据此确定系统的取货任务到达率。
双深度多层穿梭车仓储系统主要由双深度高密度存储货架、提升机、穿梭车、轨道和控制系统构成。其中,每层配置一台穿梭车,用于货物的水平运输;系统配置若干个电梯且位于货架的同一侧,用于货物的垂直运输;当穿梭车处于空载状态时可以在巷道和货架内任意移动,当穿梭车处于满装状态时只能在巷道内移动;在仓库中央设置了货物进出的缓存区,用于暂时存放货物;穿梭车将货物放置在缓存区,提升机将货物从缓存区取走,提升机和穿梭车每次只能运输一件货物。双深度多层穿梭车系统的示意图如图1所示。

双深度多层穿梭车系统的并行作业方式指穿梭车与提升机可以同时朝目标层的缓存区移动,然后进行货物交接,最后由穿梭车完成存货任务或由提升机完成取货任务。
在并行作业方式下,存货任务操作流程如下:
(1)提升机先从停留点移动至系统的I/O位置,然后将货物运送到目标层。当提升机到达目标层后,将货物放至缓存区。在提升机运行的过程中,穿梭车也从其停留点移动至缓存区。
(2)如果提升机和穿梭车都已到达缓存区,则穿梭车装载货物;如果一方未到达缓存区,则先到者需要等待另一方。穿梭车装载货物后,将其运送至指定货位,存货任务结束。
取货任务的操作流程如下:
(1)穿梭车从停留点移动至取货货位,然后运送货物至缓存区。在穿梭车运行过程中,提升机将从其停留点移动至目标层。
(2)如果穿梭车和提升机均已到达缓存区,则提升机装载货物;如果一方未到达缓存区,则先到者需要等待另一方。提升机装载货物后,将其运送至系统I/O位置。
在以上描述中,将存取任务的操作(1)中穿梭车的作业称为水平作业,提升机的作业称为垂直作业,将操作(2)称为剩余作业。在并行作业方式下,穿梭车执行水平作业的同时提升机执行垂直作业。最后由穿梭车执行存货任务的剩余作业,由提升机执行取货任务的剩余作业。本文假设穿梭车的可用状态由缓存区的状态决定,当缓存区被占用时,穿梭车不可执行取货任务。取货任务流程如图2所示。

当系统完成存取作业任务分配后,如何使穿梭车和提升机配合高效完成作业任务,是双深度多层穿梭车仓储系统作业效率优化的目的。因此,需要对穿梭车和提升机并行作业方式进行建模和求解,而建立合理的穿梭车和提升机并行作业模型是作业效率优化的关键。
2 系统建模
为建立合理正确的穿梭车和提升机并行作业模型,需要对模型的主要假设条件和参数符号进行说明。考虑单元负载式双深度多层穿梭车仓储系统,以托盘为存取单元,货物从同一出口进出,I/O位置位于货架的正下方,每个货位只能单独存放一种货物,货位的尺寸相同。同时,为了研究方便且不失一般性,进行如下假设:
(1)穿梭车和提升机服从先到先服务(First Come First Service, FCFS)原则。
(2)本文只考虑取货任务,该假设基于如下两点:①取货任务是仓储系统中关键的操作,它决定了仓储系统的服务水平;②存货任务和取货任务的操作步骤相同,如果本文模型可以较好地模拟取货任务,则也适用于存货任务。
(3)采用随机存储策略,在该策略下,每个空货位对货物存储具有相同的概率。
(4)提升机和穿梭车均服从结束点(Point of Service Completion, POSC)停留策略,即它们会停在任务结束的地方。本文以取货作业为例,提升机总停留在系统的I/O点,穿梭车总停留在缓存区旁。
本文涉及的符号参数如表1所示。

表1 主要符号参数

续表1
2.1 分离—聚合排队网络模型
定义位于第t层的取货任务为第t(t=1,2,…,T)类顾客,根据假设(3)可知,取货货物位于第t层的概率P(t)=1/T,第t层的顾客到达率λrt=λr/T。将存储货位编号为Mac(a=1,2,…,A,c=1,2,…,C),例如货位编号M25表示该货位位于第2巷道第5列,Mac的概率分布为P(Mac)=1/(A·C)。根据本文假设的POSC停留策略,穿梭车空闲时一直停在缓存区,为获得Mac处的货物,穿梭车的行走距离
(1)
式中:x1为穿梭车行走距离;a为巷道编号;c为货架列编号。
如前所述,双深度存储货架存在倒货作业现象,如图3所示,当穿梭车需要取走位于第2列的目标货物,而第1列货位被占用时,需要先将第1列货物取出并放置在倒货货位,再将目标货物取出,在此过程中,穿梭车移动的距离称为倒货距离。根据文献[10]可知,若系统中的货位占用率为α,则出现倒货作业的概率为(2α-1),穿梭车倒货距离
(2)

根据上述分析可知,水平作业的服务时间
Ts(Mac)=x1/Vs+(2α-1)·x2/Vs+εs。
(3)
因为提升机在空闲状态时位于系统I/O位置,提升机完成垂直作业需要行走的垂直距离为(t-1)H,所以垂直作业的服务时间
Tl1(t)=(t-1)H/Vl。
(4)
提升机服从POSC停留策略,剩余作业的服务时间
Tl2(t)=Tl1(t)+2εl。
(5)
基于模型假设,并行作业方式下双深度多层穿梭车仓储系统的运行过程可以等效为一个分离—聚合排队网络模型,如图4所示。
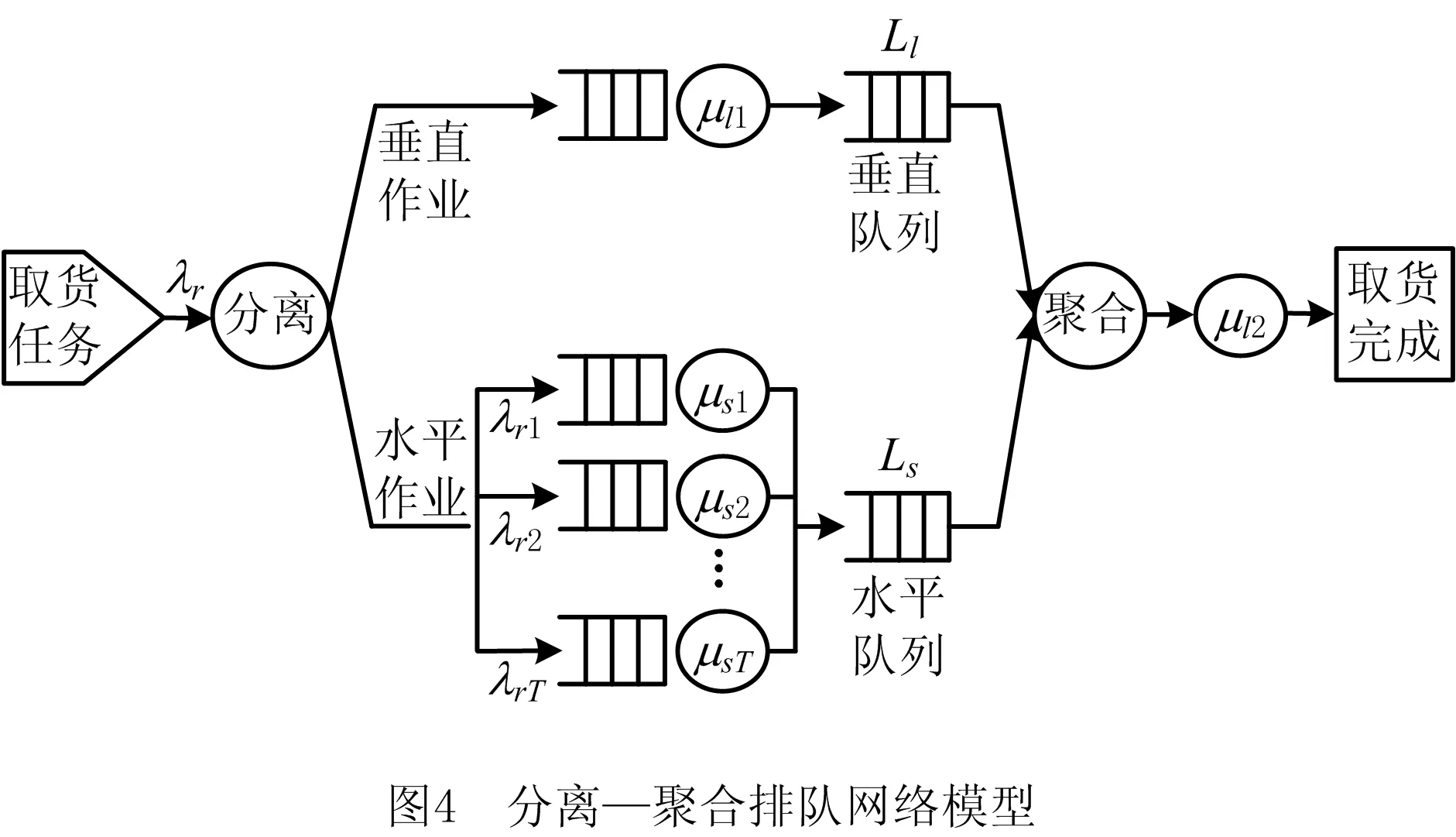
在该分离—聚合排队网络模型中,取货任务服从泊松分布,取货任务的到达率为λr。根据目标货物的所在层将取货任务分为T类,对应的到达率分别为λr1,λr2,…,λrT,μs1,μs2,…,μsT分别表示各层穿梭车的水平作业服务速率,μl1,μl2分别表示提升机在原始位置和聚合点的垂直作业服务速率。在分离点处,取货任务同时对提升机和穿梭车发出指令,然后将一个取货任务分为水平作业和垂直作业。水平作业由第t层穿梭车完成,完成后穿梭车在水平队列等待;垂直作业由提升机完成,完成后提升机在垂直队列等待。当水平作业和垂直作业都完成后,它们离开各自的队列,在聚合点处重新聚合成一个取货任务,然后移动到μl2服务点,提升机在该点进行剩余作业,即装载货物并运送至系统I/O位置。因为完成剩余作业不需要等待提升机,所以可以将μl2模拟为拥有无限服务能力。
穿梭车和提升机的作业时间均服从一般分布[12],因此该排队网络模型属于非模块形式(non-product form)排队网络,无法直接求解。本文设计了基于Coxian分布的近似分解算法来求解该排队网络模型,算法分两步:
(1)计算分离—聚合点的服务速率 构建一个包含分离—聚合点的闭环排队网络模型,将该模型中的服务点用Coxian分布近似替代,计算分离—聚合点的吞吐率,从而得到该点的服务速率。
(2)计算分离—聚合排队网络模型的系统运行性能指标 构建一个开环排队网络,将分离—聚合点用单个服务点替代,运用最大熵值法(Maximum Entropy Method, MEM)对开环排队网络模型求解,最终得到分离—聚合排队网络模型的系统响应时间、穿梭车利用率和平均等待队长等性能指标。
2.2 分离—聚合点的闭环排队网络
构建如图5所示的闭环排队网络模型,假设该模型中有Z个取货任务,每个取货任务在第t层执行的概率为1/T。令Ls为水平作业中排队等待的顾客数,Ll为垂直作业中排队等待的顾客数,则该闭环排队网络的状态变量
sk=(Ls,Ll),k=Ll(m+1)+Ls,
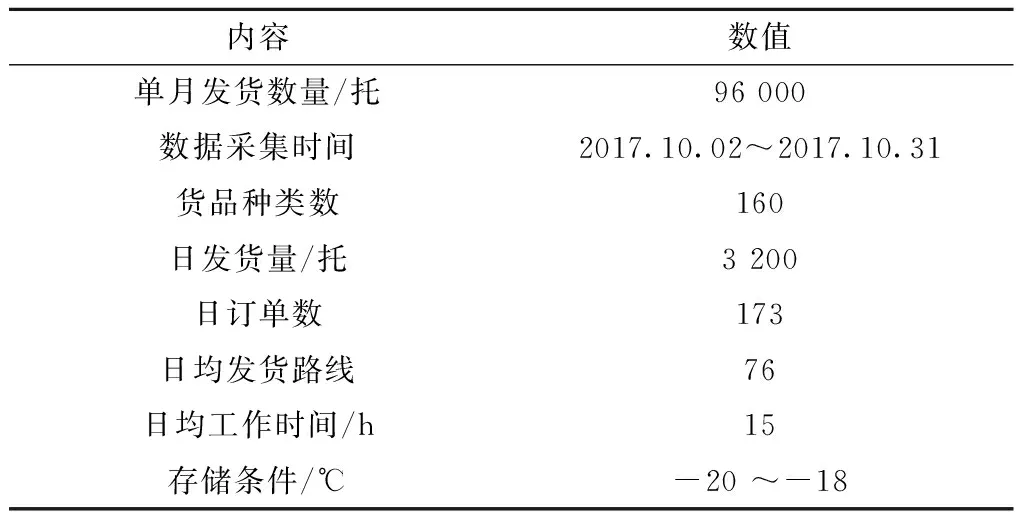
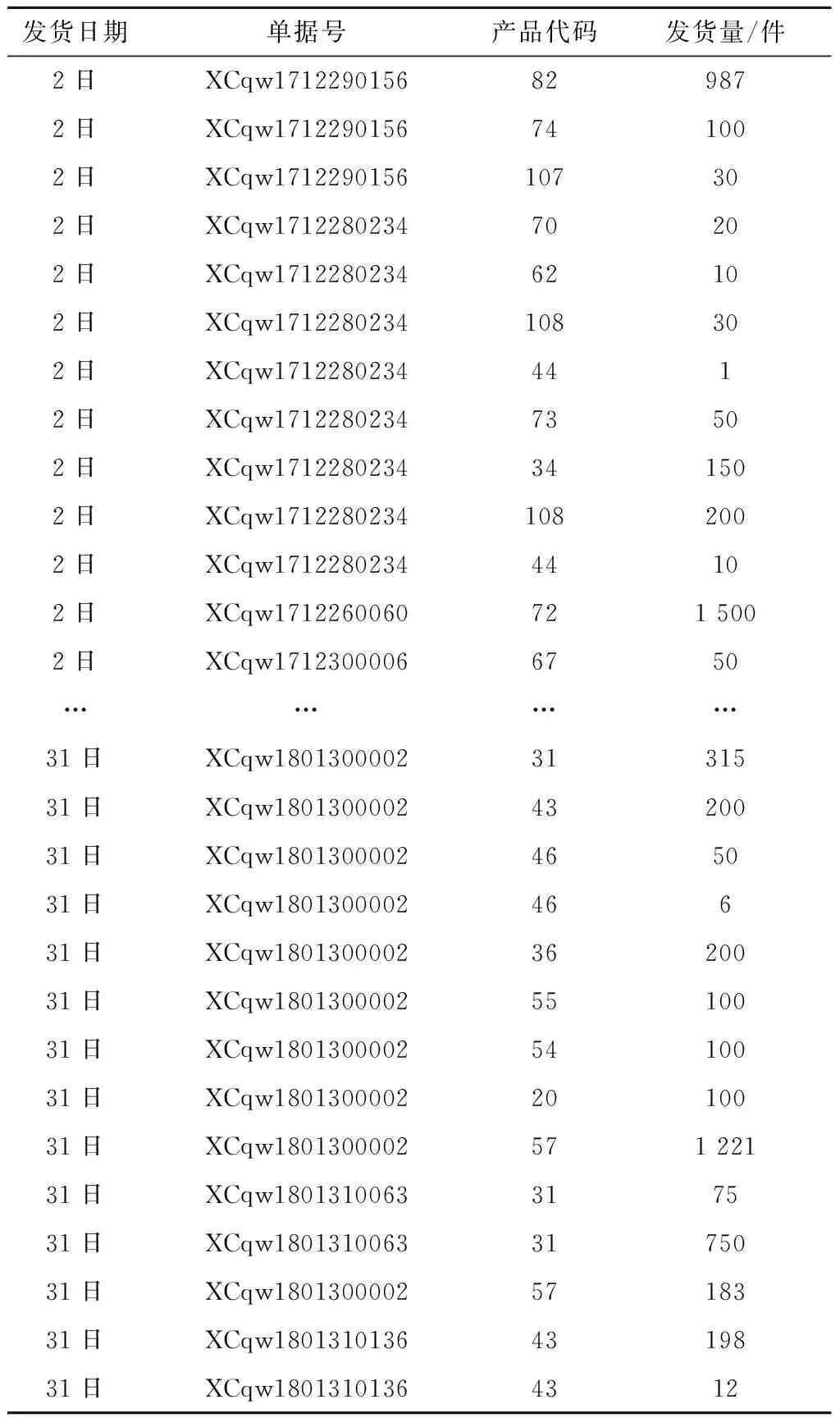
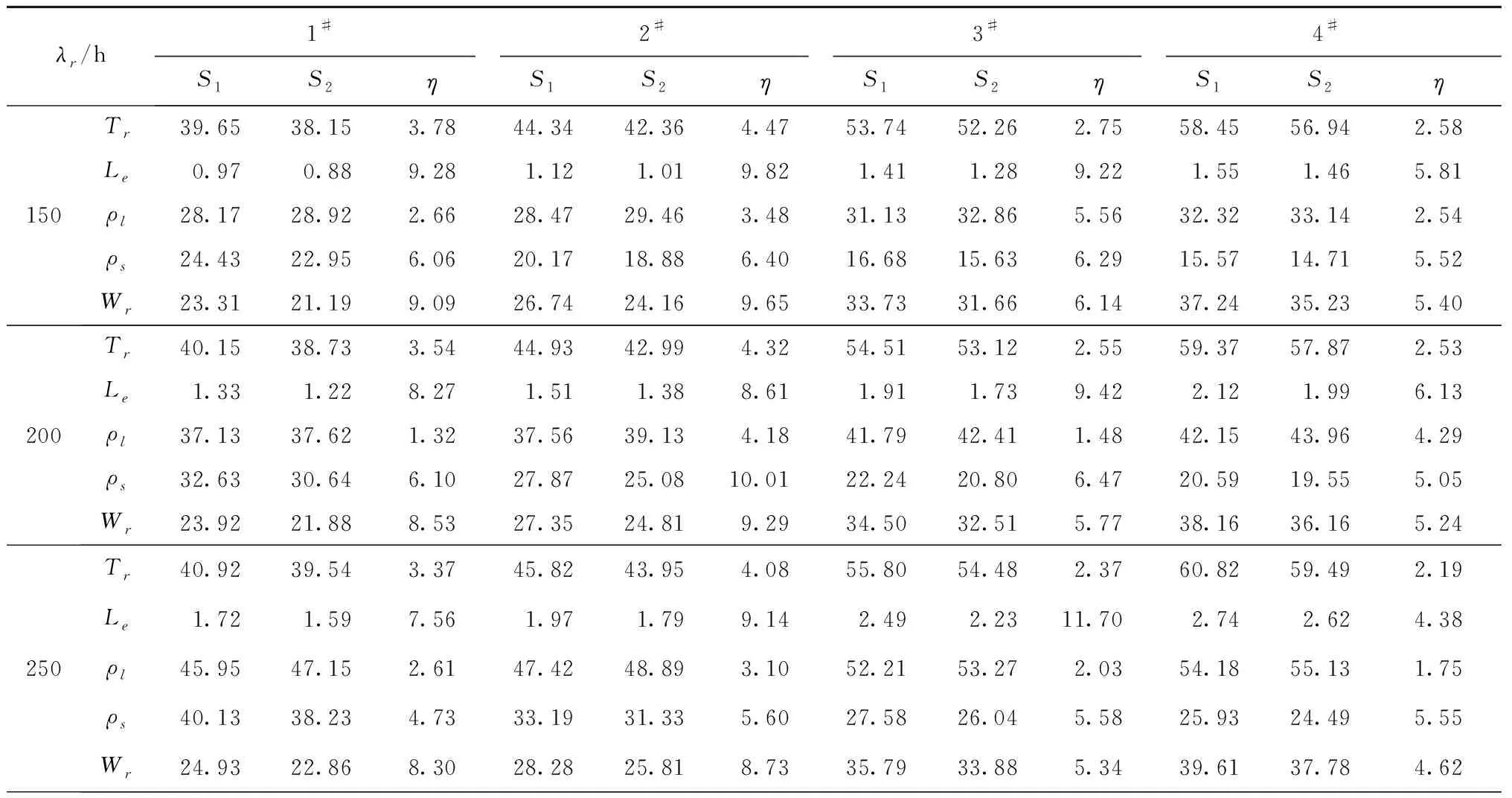
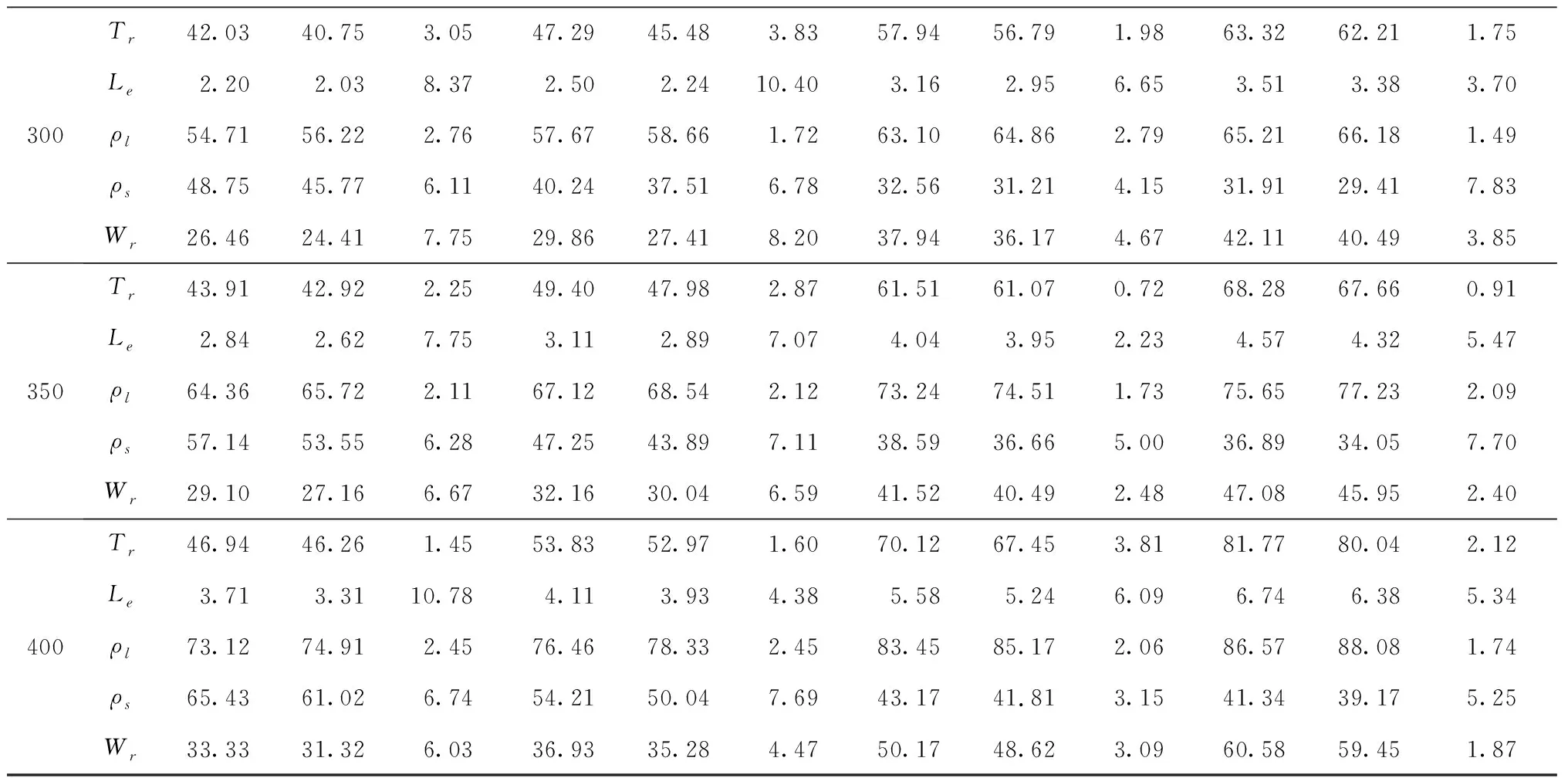
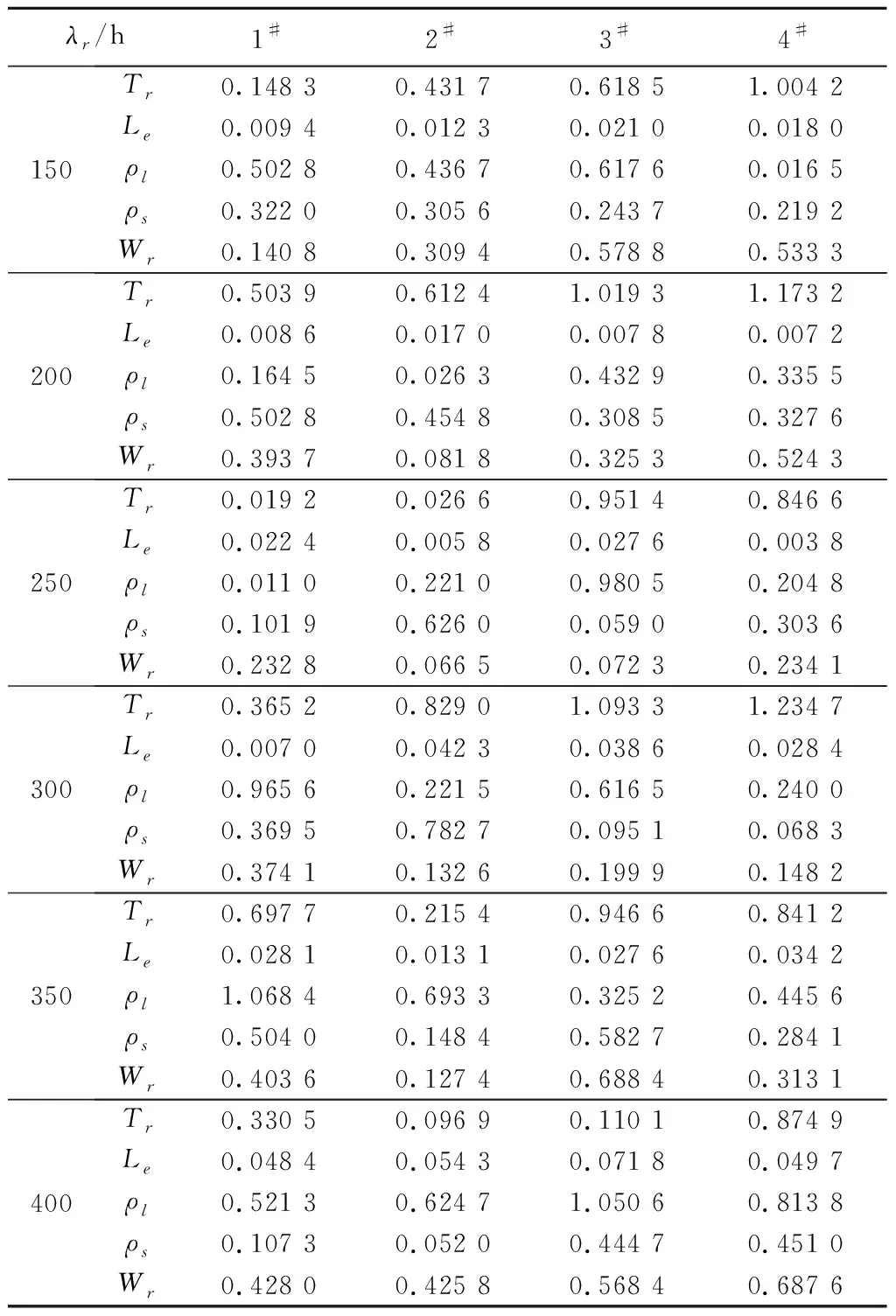
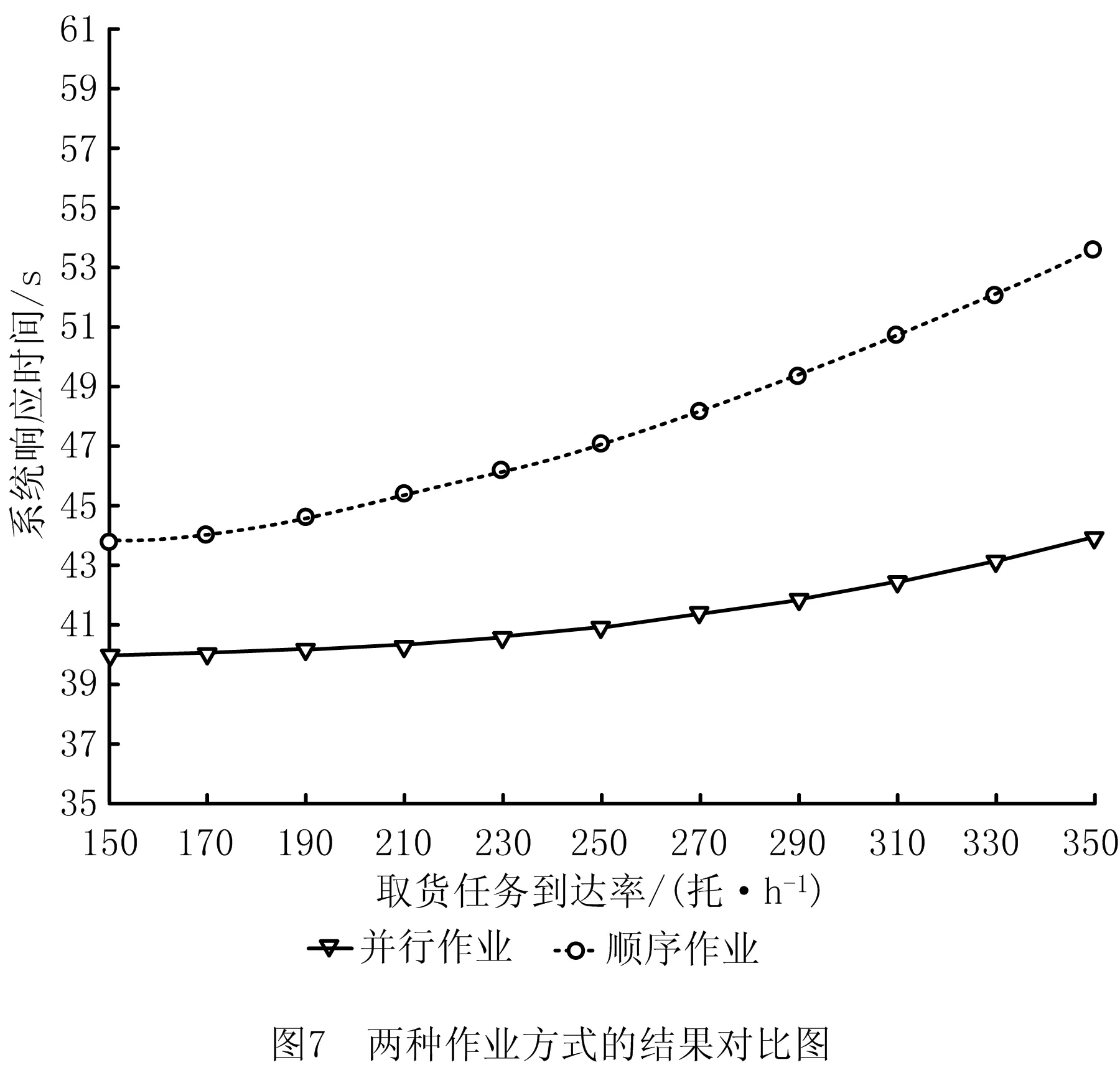
其状态空间为Ll+Ls 水平作业和垂直作业聚合包括两种情况:①当Ls>1时,完成一个垂直作业,即提升机到达目标层,该过程的服务速率为μl1;②当Ll>1时,完成一个水平作业,穿梭车到达缓存区,该过程的服务速率为μs。基于以上两种情况,分离—聚合点模型闭环排队网络的吞吐率 (6) 式中π(sk)表示sk的状态概率。 (7) (8) (9) 在该排队网络模型中,用μst表示第t层穿梭车的水平作业服务速率,根据假设(3)可知 根据式(6)计算λf(Z)需要计算闭环排队网络的状态概率π(sk)。首先,将μv服务点和μl1服务点分别用(α,T)和(β,S)的Coxian分布替换,其中α=[1 0 … 0]1×p,β=[1 0 … 0]1×q,p,q分别表示μv和μl1的Coxian分布阶数。状态转移矩阵T和S与吸收矩阵T0和S0的详细推导过程参见文献[11]。将闭环排队网络的状态变量转化为(sk,i,j),i,j(i=0,1,…,p,j=0,1,…,q)分别为穿梭车和提升机在服务过程中所处的状态。 定义稳态概率分布π(t)=[π0,π1,π2,…],Ql=0的所有状态概率向量π0=[π(s0),π(s1),…,π(sm)],Ql=1的所有状态概率向量π1=[π(sm+1),π(sm+2),…,π(s2m)],状态变量sk的转移矩阵表示为 (10) 式中:B0表示π0状态转移至π0状态的转移矩阵, (11) IT为p×p的单位矩阵,IS为q×q的单位矩阵,⊕表示克罗内克和,⊗表示克罗内克积, C0表示π0状态转移至π1状态的转移矩阵, C0= (12) A0表示π1状态转移至π0状态的转移矩阵, A0= (13) B表示π1状态转移至π1状态的转移矩阵, B= (14) C表示π1状态转移至π2状态的转移矩阵, C= (15) A表示π2状态转移至π1状态的转移矩阵, A= (16) 在稳定状态下,该排队网络满足 π(t)Q=0, (17) 由归一化条件可知 π(t)e=1。 (18) 式中e为单位向量。 根据文献[6],状态概率向量πi满足 πi+1=πiR,i≥1。 (19) 式中R为速率矩阵。联立式(17)~式(19)得到状态转移概率π(sk),将π(sk)代入式(6),得到分离—聚合点的吞吐率λf(Z)。 通过式(6)求得分离—聚合点的吞吐率,将其用单个服务点代替,并定义μFES=λf(Z),得到如图6所示的开环排队网络模型。 图中服务点1的服务速率μFES=λf(Z)。由于μFES与任务数Z相关,且服务点2的服务速率服从一般分布,根据模型判别条件可得该开环排队网络模型是一个非模块形式(non-product-form),可采用最大熵值法对该开环排队网络进行求解[13]。首先状态概率 π(k1,k2)=π(k1)×π(k2)。 (20) 式中:k1,k2分别表示服务点1和服务点2顾客的数量;π(k1),π(k2)表示服务点1和服务点2的边际状态概率。 服务点1的边际状态概率为: (21) (22) 服务点2的边际状态概率为 (23) (24) (25) (26) (27) 在求得服务点1和服务点2的边际状态概率后,由式(20)计算开环排队网络的状态概率。由此可得,服务点1的平均服务速率 (28) 服务点1和服务点2的平均顾客数分别为 (29) (30) 因此系统响应时间 (31) 取货任务在外部队列的平均等待时间 (32) 外部等待队列长度 Le=λrWr; (33) 穿梭车利用率和提升机利用率分别为 (34) ρl=1-π1(0)×π2(0)。 (35) 系统响应时间Tr、外部队列的平均等待队长Le、提升机利用率ρl、穿梭车利用率ρs和外部队列的平均等待时间Wr为表征作业效率的性能指标,用于评价双深度多层穿梭车仓储系统的作业效率。 为验证分离—聚合排队网络模型的有效性,选取郑州千味央厨的双深度多层穿梭车仓储系统一个月的发货数据进行分析。统计数据可知,该仓储系统货品种类为160种,2017年10月的发货总量为96 000托,日均发货量为3 200托,日均订单数量为173个,日均工作时间为15 h,其余数据如表2所示。郑州千味央厨仓储系统在2017年10月份发货数据如表3所示,发货周期为30 d,发货单据号为5 190个,发货总量为2 054 596件。 表2 千味央厨单月发货数据信息 表3 千味央厨10月份发货数据 本文采用4种不同配置的双深度多层穿梭车仓储系统进一步验证分离—聚合排队网络模型的合理性。如表4所示,编号分别为1#,2#,3#,4#,其中前两种代表小型仓储系统,后两种代表大型仓储系统,每层配置1台穿梭车,巷道数均为6条,提升机均为2台,其余仓储系统的主要输入参数设置如表5所示。对每种不同的系统配置,采用6种不同的输入,即取货任务到达率λr(单位:托/h)分别为150,200,250,300,350,400。 表4 4种不同的仓储系统配置方案 表5 仓储系统主要输入参数设置 通过表2和表3的原始数据计算可得,该仓储系统原来的取货任务到达率约为214托/h,采用本文方法后该仓储系统的最大取货任务到达率约为350托/h,提升系统作业效率约63.5%,证明了该方法的有效性。 为了消除初始偏差,仿真模型从第100以后取值,每个仿真方案重复运行100次,每次仿真时间为1 000 h,以达到在95%的置信水平,仿真结果的分布半长小于其均值的2%,其结果如表6所示。对Tr,Le,ρl,ρs,Wr5个系统评价指标进行分析比较,仿真结果、理论结果和误差分别用S1,S2,η表示,如表7所示,其中 (36) 表7 仿真结果与理论结果 续表7 表6 仿真结果的分布半长 由表7得到如下结论: (1)在不同系统配置和不同取货任务到达率下,系统响应时间的误差为0.72%~4.47%,平均等待队长的误差为4.38%~11.7%,提升机利用率的误差为1.32%~5.56%,穿梭车利用率的误差为3.15%~10.01%,平均等待时间的误差为1.87%~9.65%。结果表明,分离—聚合排队网络模型可以准确、有效地计算双深度多层穿梭车仓储系统并行作业下的性能指标。 (2)在取货任务到达率相同的条件下,随着系统层数的增加,平均等待时间、平均等待队长、系统响应时间、提升机利用率和穿梭车利用率均增加,这是由于系统层数增加,相应的水平作业和垂直作业时间变长,平均等待时间、平均等待队长和系统的响应时间随之变长。 (3)在同种系统配置下,随着取货任务到达率的增加,平均等待时间、平均等待队长、系统响应时间、提升机利用率和穿梭车利用率均增加。 为进一步验证双深度多层穿梭车仓储系统并行作业方式的合理性,选取郑州千味央厨的3#双深度多层穿梭车仓储系统进行分析。取货任务到达率λr从150托/h以步长为20增加至350托/h,系统响应时间的对比结果如图7所示。 根据图7结果可知,在不同的取货任务到达率下,双深度多层穿梭车仓储系统并行作业均优于顺序作业方式;随着取货任务到达率的增加,系统响应时间逐渐增大,并列作业方式的优势逐渐明显。当取货任务到达率λr=150托/h时,并行作业方式相对顺序作业方式的系统响应时间提升了9.48%;当取货任务到达率λr=350托/h时,并行作业方式相对顺序作业方式的系统响应时间提升了21.95%,从而证明该系统下采用并行作业方式能够更好地减小系统响应时间,提升系统作业效率。 并行作业方式下的系统运行总时间是提升机和穿梭车运行时间的最大值,顺序作业方式下的系统运行总时间是提升机和穿梭车运行时间的总和。采用并行作业方式虽然增加了提升机的作业负担,以及作业任务对提升机的等待时间,但是提升机能力充足,所减少的总运行时间大于所增加的等待时间,因此并行作业方式可以减小系统响应时间,提升系统作业效率。 上述研究结果表明,分离—聚合排队网络模型能够快速、有效地分析系统运行性能指标;并行作业方式能够减小系统响应时间,提高系统柔性。另外,仓储系统可根据性能指标调整穿梭车和提升机的数量,从而节约系统运行成本,该方法可以为并行作业方式下的作业任务调度和路径优化提供理论依据。 本文针对双深度多层穿梭车仓储系统并行作业流程提出分离—聚合排队网络模型,并通过分离—聚合点的闭环排队网络模型和基于分离—聚合点的开环排队网络模型分别对分离—聚合点的服务速率和系统运行指标进行求解。最后,对4种不同配置的仓储系统进行分析,结果表明,分离—聚合排队网络模型可以准确、有效地反映双深度多层穿梭车仓储系统并行作业下的各项性能指标,与传统顺序作业方式相比并行作业可以减小系统响应时间9.48%~21.95%,从而较大幅度地提高系统作业效率。为进一步提高仓储系统吞吐能力,未来将对货物分类存储策略和基于周转率存储策略进行研究。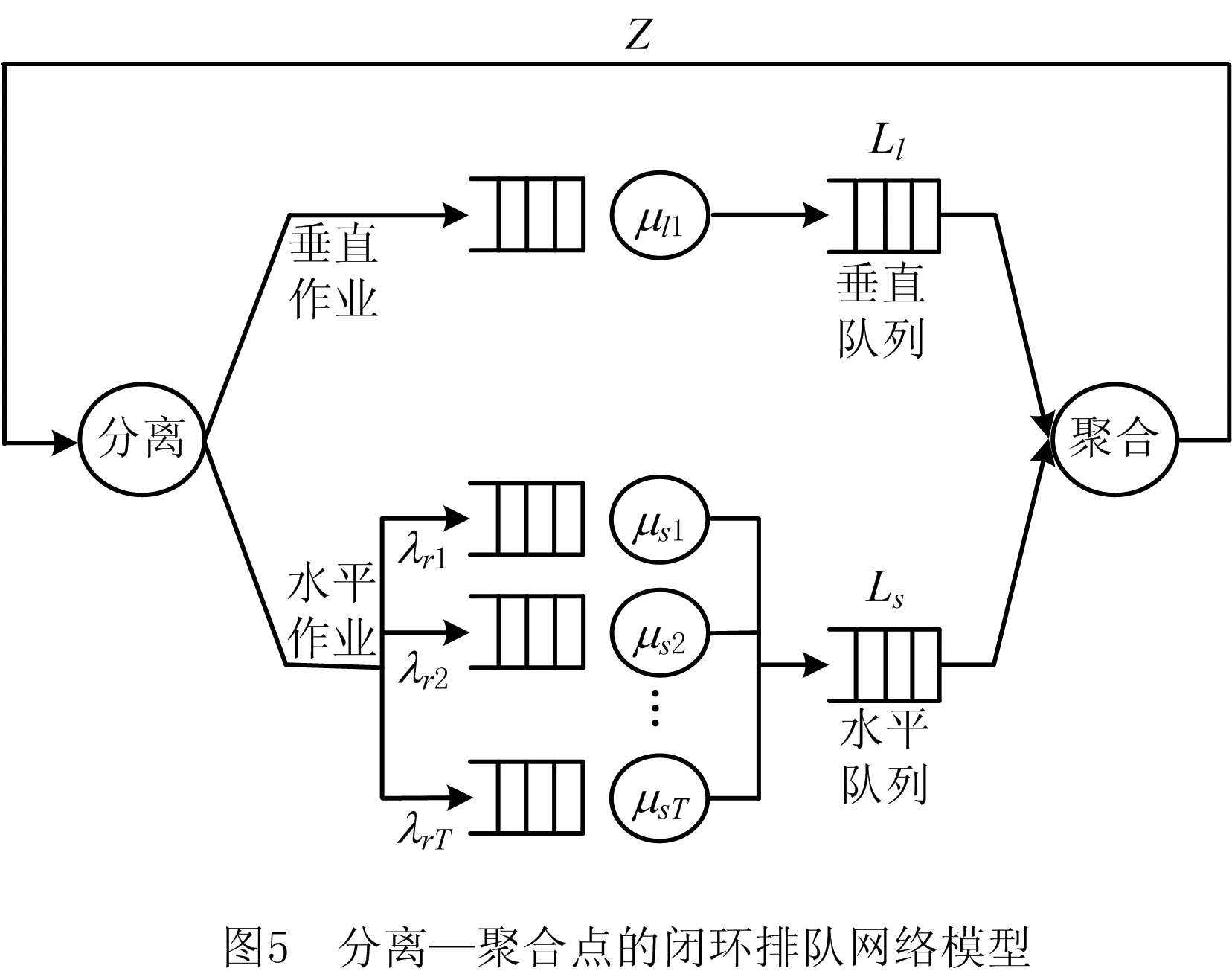
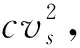
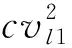
2.3 基于分离—聚合点的开环排队网络模型

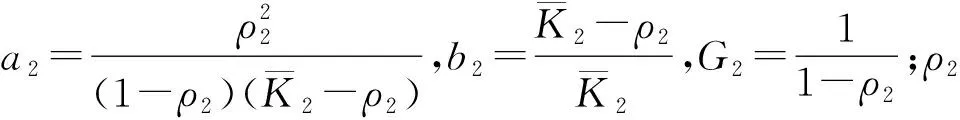
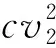

3 案例分析
3.1 案例验证


3.2 作业方式对比
4 结束语
