基于极半径曲面矩和HMM的三维模型分类与检索算法

王洪申，刘 敏，强会英

（1.兰州理工大学机电工程学院，甘肃兰州730050；2.兰州交通大学数理与软件学院，甘肃兰州730070）

随着计算机辅助设计（computer aided design，CAD）技术的发展和应用，企业积累了大量工程数据。工程数据中蕴含着丰富的专业知识，如何处理和分析这些工程数据并从中提炼出可重用的信息是一个亟待解决的问题。三维CAD 模型作为机械设计的产物，其数量巨大，这些三维CAD 模型中蕴含着大量可重用的设计信息。为了能有效地利用这些信息，须对三维CAD模型的分类与检索方法进行研究，且提高检索的准确率和效率是关键。

不变矩是分类问题中重要而有效的特征量［1］，利用不变矩来提取三维模型的特征既简单又快速。但是，在目前关于不变矩的研究中，大多采用Hu 不变矩［2］、Zernike 矩［3］和仿射不变矩［4-5］等图像不变矩来提取三维模型的特征，使用时必须先将三维模型转化为二维图像，再利用图像不变矩来提取特征，这可能会导致三维模型的特征信息丢失并引入新的干扰信息。例如：曹茂永等［6］采用极半径不变矩对二维图像的形状进行识别；李宗民等［7-8］提出了极半径曲面矩，通过实验验证了其平移、缩放和旋转不变性，并利用极半径曲面矩评价了三维模型的相似性。研究表明，极半径曲面矩能有效提取三维模型的几何特征，避免了三维向二维的转换过程，基于极半径曲面矩的分类与检索方法可稳定、可靠地识别并区分三维模型的形状差异，从而保证三维模型分类与检索的准确性。

隐马尔可夫模型（hidden Markov model，HMM）［9］是一种可用于标注问题的统计分析模型，具有很强的学习能力和模式分类能力。HMM 描述的是一个含有隐含未知参数的马尔可夫过程，其状态不能直接被观察到，但可通过观测随机序列观察到，其中每个观测序列是由1个具有相应概率密度分布的状态序列产生的。HMM 可被视为一个具有双重随机过程的有限状态自动机，其每个状态都代表一个可观察的事件，状态之间的转换都可以用一定的概率来表示［10］。目前，HMM 已成功应用于语音识别、行为识别、文字识别以及故障诊断等［11］。三维模型分类的目标是将未标注的三维模型划分到某个预设的模型类别中［12］。但对于数量庞大的三维模型来说，利用人工标注来分类是不可取的，而HMM 可有效解决该问题。

基于此，笔者拟采用极半径曲面矩和HMM 来实现机械零件三维模型的分类与检索。首先，通过计算极半径曲面矩来提取三维模型的特征，并将排序编码后的特征向量作为HMM 的观测序列；然后，选取部分人工标注过的三维模型作为训练样本，采用添加比例因子的多观测序列B-W（Baum-Welch）算法对HMM 进行训练；最后，利用训练好的HMM对三维模型进行分类与检索。

1 基于极半径曲面矩与HMM 的三维模型分类与检索算法的原理

1.1 三维模型的特征提取

极半径曲面矩是一种具有平移、缩放和旋转不变性的不变量，其既可作为由连续区域构成的三维模型的特征量，也可作为由分离区域组成的三维模型的特征量［8］。极半径曲面矩的形式简洁，可直接通过读取三维模型表面的网格数据来计算，而不用对三维模型进行体素化处理。

对于由三角面片构成的三维模型，用D表示其表面区域，A表示其表面积，(xc，yc，zc)表示其形心的坐标，r表示三角面片上的点到形心的距离，r=，则该三维模型的第p阶极半径曲面矩mp和极半径曲面中心矩mcp为：

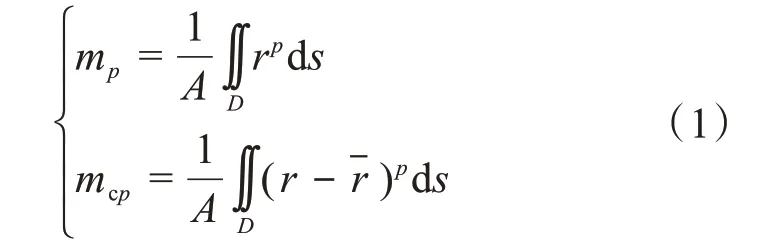
式中：ds为积分区域的微元；为极半径平均值，。

归一化后第p阶极半径曲面矩和极半径曲面中心矩为：

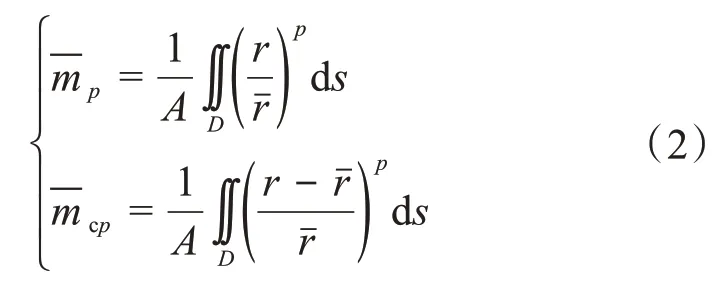
用离散形式表示归一化后的第p阶极半径曲面矩和极半径曲面中心矩，为：

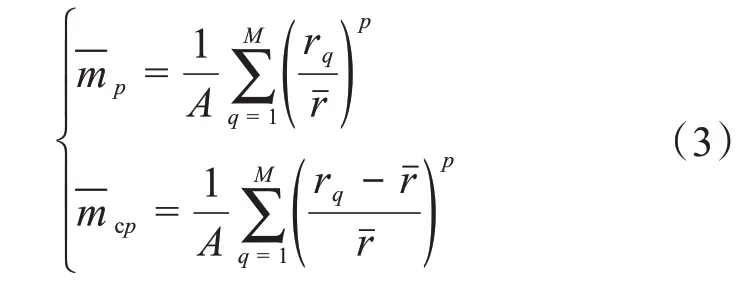
以STL（stereolithography，立体光刻）格式的三维模型文件为例，基于遍历获取的三维模型表面网格数据，通过计算得到由极半径曲面矩和极半径曲面中心矩组成的组合不变矩，并将其作为模型的特征向量。通过试验发现，偶数阶的极半径曲面矩的区分度较好，同时为了减小计算量，选取第4，6，8，10 和12 阶极半径曲面矩以及第2，4，6，8 和10 阶极半径曲面中心矩组成十维组合不变矩(m4，m6，…，m12，mc2，mc4，…，mc10)。

提取了三维模型的特征后，采用排序编码的方式将组合不变矩转换为HMM 的输入观测序列。具体方法如下：假定有L个三维模型，预设分类为K类，每个模型均用十维组合不变矩表示，首先将模型的每一维特征值按从小到大的顺序排列，然后将同一维排列好的L个特征值按大小排序后再平均分为K份，第1 份特征值全编为0，第2 份特征值全编为1……第K份特征值全编为K-1，从而获得排序编码后的十维特征向量。

1.2 基于B-W算法的HMM训练

将排序编码后的特征向量作为HMM 的输入观测序列，并采用添加比例因子的多观测序列B-W 算法［1，13］对HMM进行训练（B-W算法可有效减少HMM训练所需的样本数量），以获得优化的HMM。

设添加比例因子的HMM 为λ，训练好的HMM为。t时刻下HMM 的观测序列O对应的前向概率和后向概率分别为［14］：

式中：N为HMM 中状态的数量，分别为用于计算前向概率和后向概率的中间变量；ct是添加的比例因子；aij(aji)为状态i(j)向状态j(i)转移的概率；bi(Ot)、bj(Ot+1)分别为观测序列O在时刻t下对应状态i和时刻t+1下对应状态j的观测概率。

对于HMM中第l（1≤l≤L）个观测序列Ol，其在t时刻的隐状态为Si的概率为：

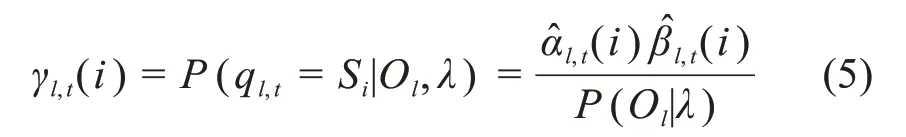
HMM 中第l个观测序列Ol在t时刻的隐状态为Si且在t+1时刻的隐状态为Sj的概率为：

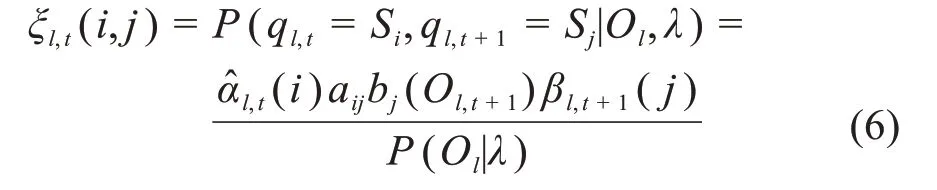
由此可得，HMM参数的重估公式为：

式中：Tl为观测序列Ol的训练时序；cl，t为观测序列Ol的比例因子；k为观测序列的观测值。

利用参数重估公式对HMM进行训练，得到优化的HMM，具体流程如图1所示。

图1 基于B-M算法的HMM训练流程Fig.1 Training process of HMM based on B-M algorithm

2 基于极半径曲面矩与HMM 的三维模型分类与检索算法的实现与检验

2.1 算例设计

在普渡大学工程标准模型库［15］中选取5 类零件的三维模型，每类模型均有10个相似模型。计算各个三维模型的极半径曲面矩和极半径曲面中心矩，组成十维组合不变矩，再用排序编码的方式将其转化为HMM的观测序列。取每类零件中的5个三维模型用于HMM的训练，最终得到对应于不同零件的5个优化的HMM。HMM的状态数量为5，状态转移概率矩阵A与观测概率矩阵B随机生成，初始状态矩阵π=[0.2 0.2 0.2 0.2 0.2]。所选取的5类零件的代表模型及其组合不变矩如表1所示。

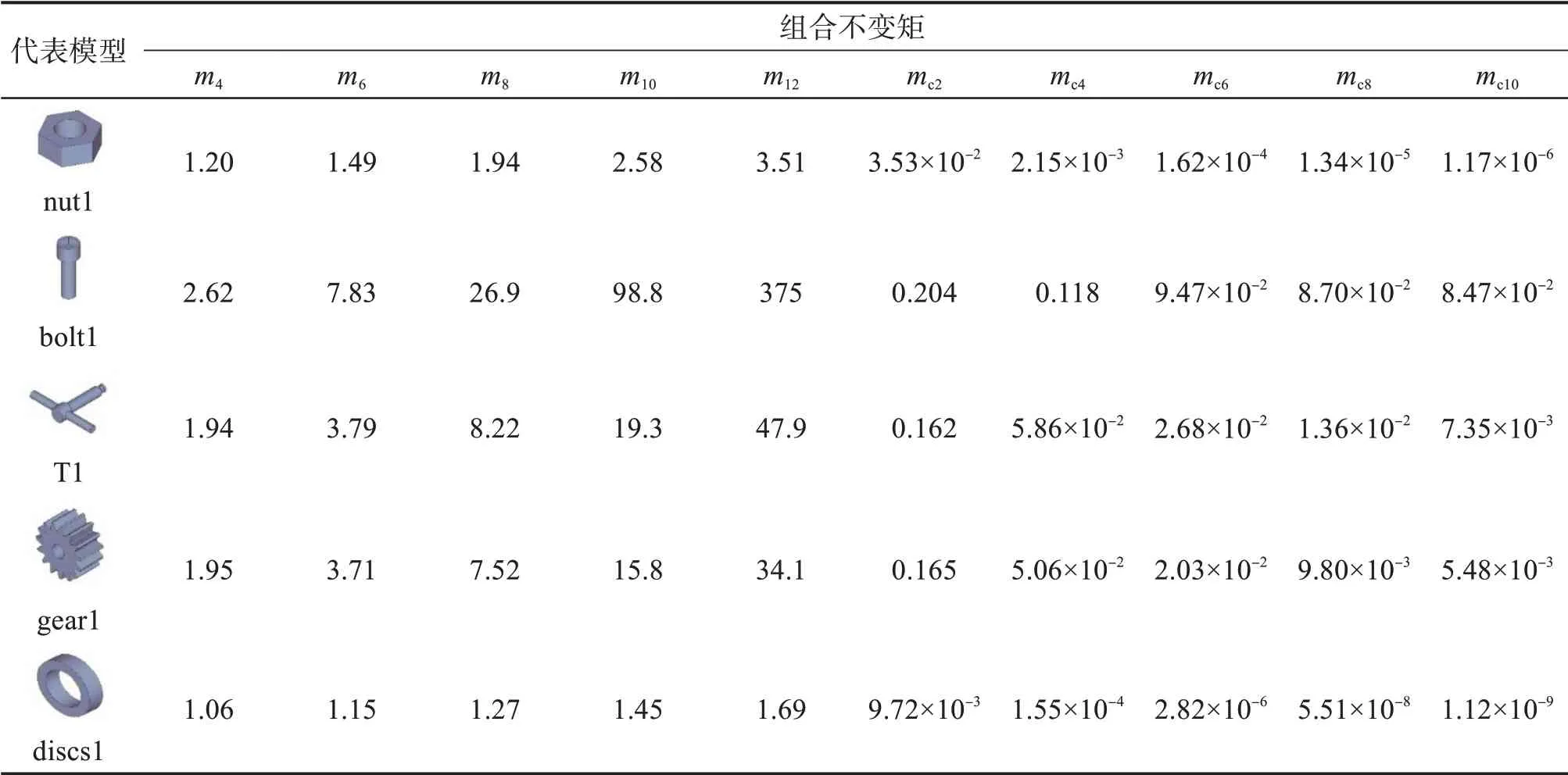
表1 5类零件的代表模型及其组合不变矩Table 1 Representative models of five types of parts and their combined moment invariants

模型分类：将排序编码后的50个三维模型的特征向量分别输入训练好的5个HMM中，计算它们在5个HMM中的观测序列出现概率，将其标注为概率最大的HMM所对应的零件类别。

模型的检索：用极半径曲面矩+一阶Minkowski相对距离（即闵式相对距离）作为相似性判断指标，即计算得到的一阶闵式相对距离越小，三维模型的相似性越高。在模型分类完成后，当查找某个特定模型时，先在相似的类中用一阶闵式相对距离直接检索，以加快检索效率，必要时可以直接利用极半径曲面矩+一阶闵式相对距离对所有模型进行检索，以找出所有相似模型。一阶闵式相对距离d的计算式为：

式中：xh、yh为要计算相对距离的2个极半径曲面矩。

2.2 算法的性能比较

将基于极半径曲面矩和HMM 的分类与检索算法记为算法A；基于极半径曲面矩和一阶闵式相对距离的分类与检索算法［7］记为算法B；基于Hu不变矩、仿射不变矩和HMM的分类与检索算法［1］记为算法C（使用canny算子，阈值为0.3）。表2所示为基于不同算法的5类零件的三维模型分类结果，表3至表5所示为是基于不同算法的nut类、bolt类和T shape类零件三维模型的检索结果（由于篇幅限制，只列出3类零件的检索结果）。图2所示为基于不同算法的nut类、bolt 类和T shape 类零件三维模型的检索效率曲线。表6所示为3 种算法的平均精度（mean average precision，mAP）。根据上述结果，对比算法A和算法C可得，利用极半径曲面矩能够更好地提取三维模型的特征；对比算法A 和算法B 可得，用HMM 作为分类器能够得到更好的分类效果。

表6 3种算法的平均精度对比Table 6 Comparison of average accuracy of three algorithms

图2 基于不同算法的3类零件的三维模型检索效率对比Fig.2 Comparison of retrieval efficiency of three-dimensional models of three types of parts based on different algorithms

表2 基于不同算法的5类零件的三维模型分类结果Table 2 Classification results of three-dimensional models of five types of parts based on different algorithms

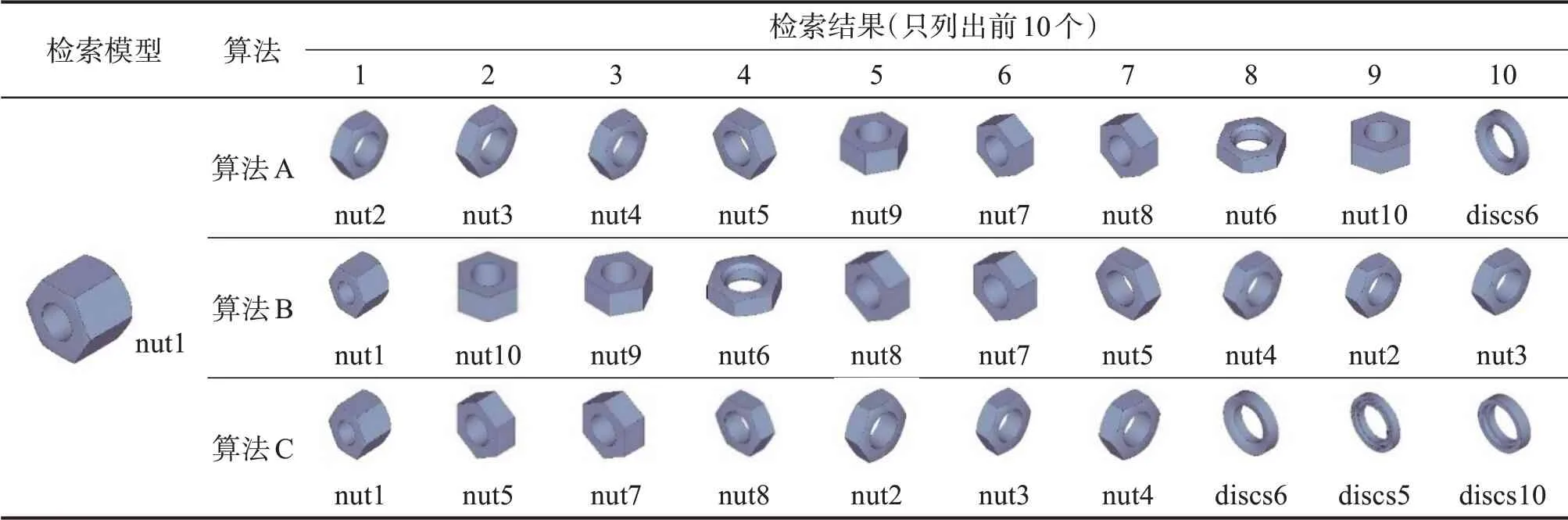
表3 基于不同算法的nut类零件三维模型的检索结果Table 3 Retrieval results of three-dimensional models of nut type parts based on different algorithms

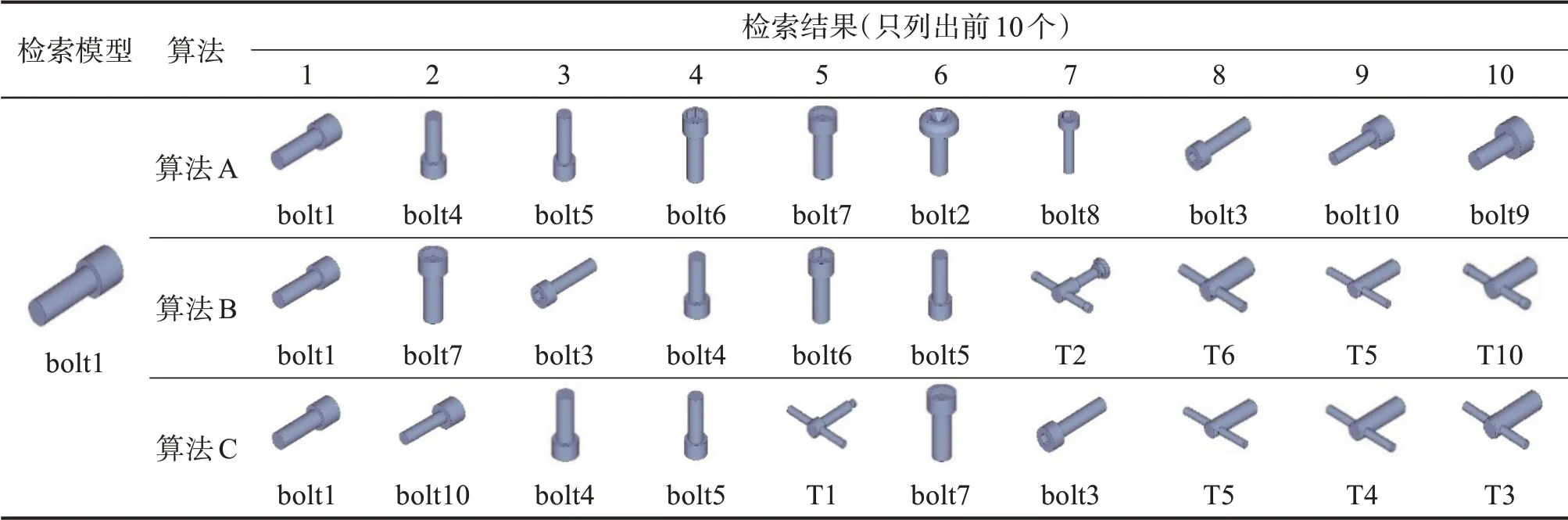
表4 基于不同算法的bolt类零件三维模型的检索结果Table 4 Retrieval results of three-dimensional models of bolt type parts based on different algorithms

表5 基于3种算法的T shape类零件三维模型的检索结果Table 5 Retrieval results of three-dimensional models of T shape type parts based on different algorithms

为进一步验证本文算法的可靠性，扩大试验样本，从PTC（parametric technology corporation，参数技术公司）的标准件库［16］中选取3类零件（flanges类、nut 类、screw 类），每类零件有100 个相似模型，每个模型均符合相应类的国标，且尺寸都不相同，保证差异性，部分代表模型如表7所示。HMM 的状态数设为3，状态转移概率矩阵A与观测概率矩阵B随机生成，初始状态矩阵π=[0.3 0.3 0.4]。基于算法A、B、C 的3 类零件的三维模型分类结果如表8所示（HMM 的训练样本数量为40个）。在不同数量训练样本下基于本文算法的3类零件的三维模型分类结果如表9所示。

表7 部分所选零件的代表模型及其对应国标Table 7 Representative models of some selected parts and their corresponding national standards

结合表2和表8可以看出，基于Hu不变矩、仿射不变矩和HMM 的分类与检索算法的分类准确率最低，主要原因是该算法用二维图像矩作为三维模型的特征描述子，而三维模型转化为二维图像时损失了大部分特征，且用图像矩提取二维图像特征时存在噪声干扰，若调高边缘检测算法中canny 算子的阈值，则会丢失细节，从而导致分类的准确性降低。在对nut类零件的三维模型进行分类时，算法C误判了大量的异形螺母，比如六角锁紧螺母、盖型螺母和开槽螺母，由此说明基于Hu不变矩、仿射不变矩的算法易被复杂特征干扰，提取特征时的鲁棒性不高。利用本文基于极半径曲面矩和HMM 的分类与检索算法得到的分类结果的准确率较高，这是因为利用极半径曲面矩提取三维模型特征时的稳定性好，且HMM具有较强的抗干扰能力，采用添加比例因子的多观测序列B-W 算法能训练出泛化能力更强的HMM。从表9中可以看出，基于极半径曲面矩和HMM的检索与分类算法的分类准确率随着训练样本数量的增加而提高，由此说明该算法具有自我进化的能力，可随着训练次数的增加而不断提高性能。

表8 基于不同算法的3类零件的三维模型分类结果Table 8 Classification results of three-dimensional models of three types of parts based on different algorithms

表9 不同数量训练样本下基于本文算法的3类零件的三维模型分类结果Table 9 Classification results of three-dimensional models of three types of parts based on algorithm in this paper under different numbers of training samples

3 结论

本文使用极半径曲面矩提取三维模型的特征并构成组合不变矩，再将其排序编码以作为HMM的观测序列；运用人工标记的三维模型和添加比例因子的多观测序列B-W 算法来训练HMM，再用训练好的HMM 对未标记的三维模型进行分类与检索。本文算法以提取的三维模型的极半径曲面矩为特征描述，可以避免对三维模型的体素化处理，提高了检索效率，与使用二维图像矩提取三维模型特征的方法相比，减少了信息的丢失和新噪声的混入；本文算法引入了HMM，在实际应用中可以用已正确分类的三维模型来训练HMM，提高了分类与检索的准确率。将本文算法与基于极半径曲面矩和一阶闵式相对距离的分类与检索方法以及基于Hu不变矩、仿射不变矩和HMM的分类与检索方法进行了对比。结果显示，本文算法对三维模型的分类与检索效果更好，具有一定的实用价值。