双论域多粒度模糊粗糙集近似的并交关系

陈 江， 张贤勇， 莫智文

（四川师范大学 数学科学学院 智能信息与量子信息研究所，四川 成都610066）

模糊集与粗糙集是2种基本的不确定性模型，两者结合的模糊粗糙集与粗糙模糊集能够系统探寻不确定性［1］，其中模糊粗糙集将经典粗糙集中的等价关系推广到模糊关系，成为一种强健的不确定性处理模型［2-4］，其深入拓展能够更好获取适用性与优效性，相关构建主要涉及“多粒度深化”与“双论域推广”.

多粒度深化技术聚焦一族等价关系，集成构建概念的悲观近似与乐观近似，从而建立多种多粒度粗糙集模型［5-6］，具有拓展研究与实际应用价值［7-8］.此外，双论域推广是拓展经典粗糙集的又一方向，双论域粗糙集具有诸多研究［9-10］，并产生了双论域模糊粗糙集［11-12］.在此基础上，模糊粗糙集已经拓展到多粒度模糊粗糙集［13-14］、双论域模糊粗糙集［11-12］、双论域多粒度模糊粗糙集［15-16］，而双论域多粒度模糊粗糙集最终成为一类重要模型.

双论域多粒度模糊粗糙集能够有效处理多粒度与双论域问题，具有研究意义.对此模型，文献［16］研究双论域上基于多粒度模糊概念的粗糙逼近问题；文献［17］研究上下近似的包含条件，并给出一种标准化方法.上下近似关于并交运算的系统性质是近似逼近与逻辑融合的基础，它们基本存在于经典粗糙集模型，但尚未涉及到双论域多粒度模糊粗糙集.本文主要探讨双论域多粒度模糊粗糙集近似的并交关系，并对比分析关于经典粗糙集模型的异同性，从而揭示相关的扩张特性.

1 双论域多粒度模糊粗糙集

这里简要回顾双论域多粒度模糊粗糙集，为后续并交系统分析奠定基础.

定义1［18］论域U、V为2个非空有限集合，R={R1，R2，…，Rm}是从U到V的二元模糊关系簇，其中Rt∈F（U×V）（t=1，2，…，m）.有序三元组（U，V，R）称为双论域多粒度模糊近似空间.

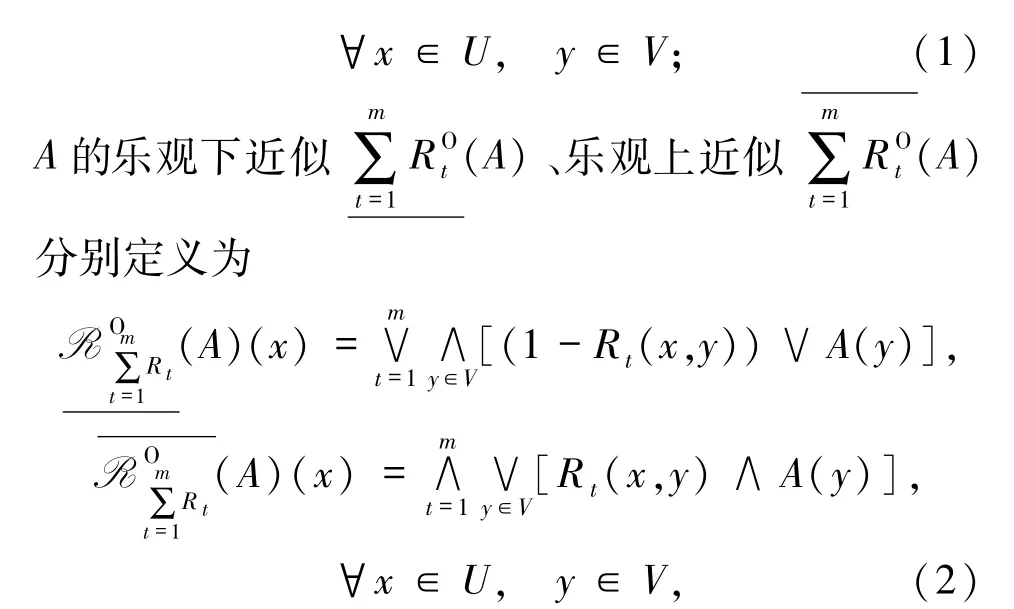
其中，∧、∨分别为取小、取大运算.

下面提供一个实例来说明双论域多粒度模糊粗糙集，主要说明其中的悲观、乐观双近似性质.

例1在医疗诊断中，设疾病集U=｛病毒性发热，痢疾，伤寒｝=｛x1，x2，x3｝，症状集V=｛发烧，头痛，胃痛｝=｛y1，y2，y3｝，Rt（t=1，2，3）∈F（U×V）是3个专家分别给出的U到V关系，其中

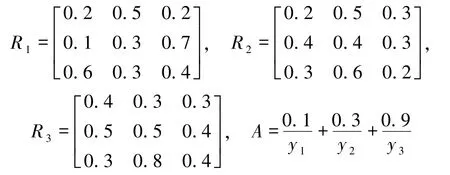
为病人对自己病情的描述.

令R=｛R1，R2，R3｝，则对于疾病x1、x2、x3，利用（1）式考虑悲观情况，此时专家判断病人A患有疾病x1的双近似估计为

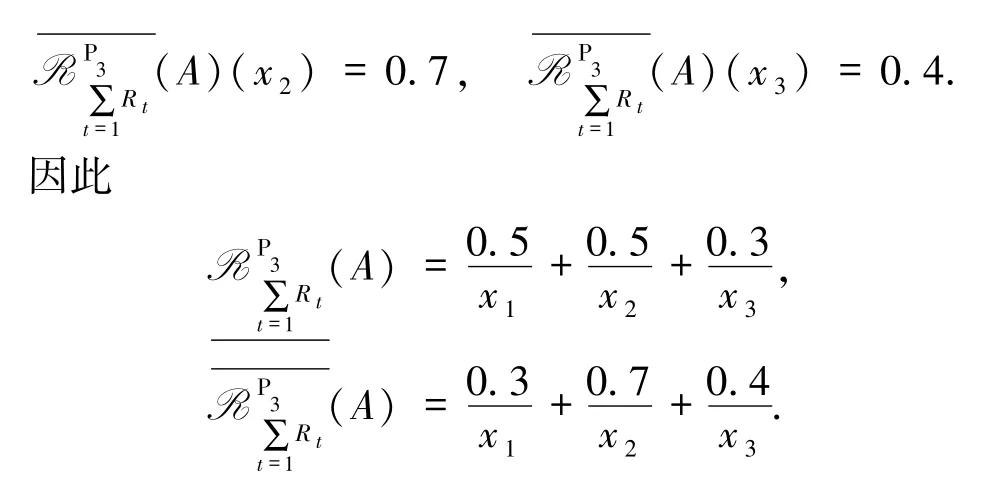
再考虑乐观模型，利用（2）式可以进行类似悲观模型的计算方法，结果为

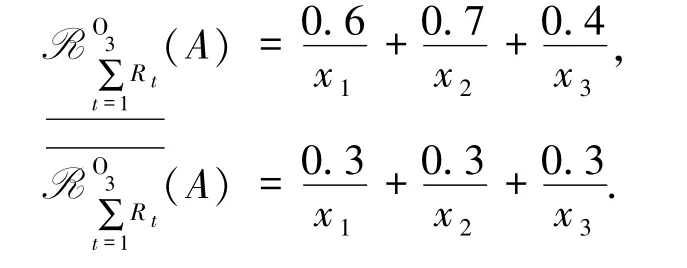
2 双论域多粒度模糊粗糙集的双近似并交性质

双论域多粒度模糊粗糙集的类似情形值得探讨，本节分悲观与乐观2种情形来研究相关的双近似并交系统性质.在双论域多粒度模糊近似空间（U，V，R）中，下设模糊集A，B∈F（V）.

2.1 悲观情况下的双近似并交性质

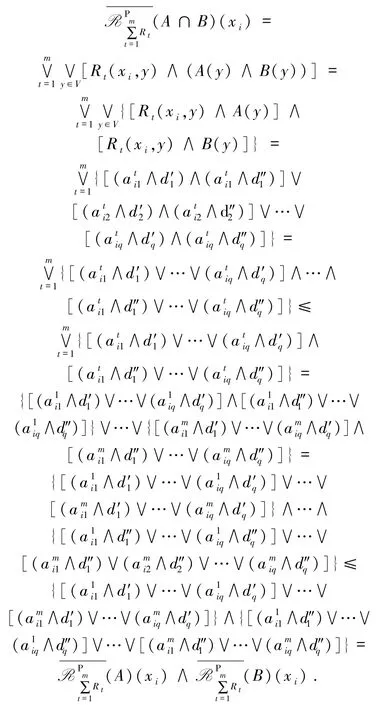
针对悲观情况，性质1～性质4提供了双论域多粒度模糊粗糙集的双近似并交性质，其与经典粗糙集模型的结果（（3）式）完全一致，这表明了模型扩张的正常性.

2.2 乐观情况下的双近似并交性质上面提供了悲观情况下的双近似并交性质，下面转向对称的乐观情况，得出更一般的子集关系或超集关系.相关证明可以类似进行，下面采用近似算子的单调性这一新策略.

引理1若A′⊆A″，则

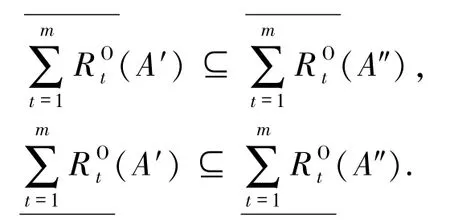
证明由（2）式有

引理1表明乐观上下近似算子均具有关于集合包含的单调性.由此，可以直接得到下述乐观上下近似的并交性质，其中涉及到基本关系：A∩B⊆A⊆A∪B，A∩B⊆B⊆A∪B.

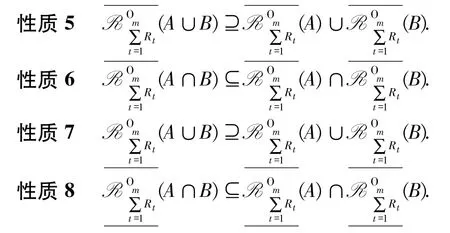
针对乐观情况，性质5～性质8提供了双论域多粒度模糊粗糙集的双近似并交性质.对比经典粗糙集模型的结果（（3）式），性质5、性质8呈现微观差异性，性质6、性质7具有完全一致性，这表明了模型扩张的特异性.

分析悲观与乐观上下近似算子的运算机制（参见（1）（2）式），悲观上下近似算子对粒度的集成运算与对论域V中单元的集成运算一致，而乐观上下近似算子相反.同时结合∨、∧运算性质中的分配律与结合律，对比经典粗糙集模型的结果，悲观上下近似算子并交运算的相等关系得以保持，而乐观上下近似算子并交运算的相等关系不再成立.下面主要分析差异性来源.具体地，在乐观情况中，对∀x∈U，有

等号不成立，故性质5只能得到包含关系的一般结论.

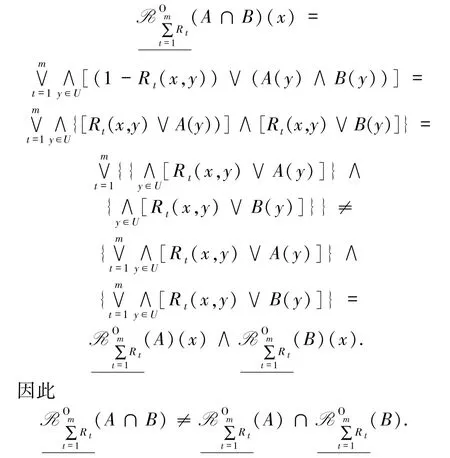
等号不成立，故性质8只能得到子集关系的一般结论.

通过上述分析，乐观上下近似算子对于粒度的集成运算和对论域中单元集成运算的不一致性，是导致不同于经典粗糙集结果的原因，也是导致悲观近似算子与乐观近似算子性质的差异性的原因.乐观近似算子性质（主要是性质5、性质8）具有拓展性而非保持性，在多粒度环境下，能否一定达到保持条件或者在什么条件下可以达到保持条件成为一个问题.考虑到多粒度具有向单粒度的退化性，下面通过条件m=1自然得到一种基本的等号保持性关系.

3 实例分析

本节提供实例分析，具体说明双论域多粒度模糊粗糙集的并交关系，即上述性质1～性质8.

例2这里采用例1的数据与结果，其中A的双论域多粒度模糊粗糙集双近似如下：

从而性质5～8的并交关系成立.

4 结束语

对比经典粗糙集的近似并交性质，本文研究了双论域多粒度模糊粗糙集的近似并交性质并给予实例验证，得到了后者在模型扩张时产生的系统性与特异性.根据性质1～性质8，在双论域多粒度模糊粗糙集的乐观情况下，并的上下近似总是包含上下近似的并；而交的上下近似总是包含于上下近似的交，性质5、性质8与经典模型的传统相等结果（（3）式）有所差异，其他结果则是完全一致的.进而，模型满足什么条件时，性质5、性质8可能达到等号（即乐观近似算子具有对比经典情况的保持性）成为一个问题.考虑到经典粗糙集具有关于平凡集、子集、并交补运算、幂作用的系统性质，因而双论域多粒度模糊粗糙集也值得进行类似的系统研究.对此，文献［17］讨论了子集关系，本文讨论了并交关系，剩余的情形还需要深入研究.