一种基于K-shell影响力最大化的路径择优计算迁移算法

乐光学 陈光鲁 卢 敏 杨晓慧 刘建华 黄淳岚 杨忠明

1(嘉兴学院信息科学与工程学院 浙江嘉兴 314001) 2(国网冀北电力有限公司大城县供电分公司 河北廊坊 065000) 3(江西理工大学理学院 江西赣州 341000)

随着通信技术与智能终端设备的快速发展和应用普及，流式服务已成为移动网络承载的重要业务之一，对智能终端设备性能提出了更高的要求.受计算能力、存储容量、电池能耗、设计美观等限制，移动智能设备(mobile smart device,MSD)无法完成资源需求大、计算任务重的密集型任务.为解决该问题，资源丰富的云计算模型作为有效方案之一应运而生，并由此已演化出雾计算、边缘计算等先进的计算模式.5G技术的日渐成熟和应用推广，使得无线移动网络承载数据和业务量将以线性增长，流式多元化网络业务和服务的快速增长必将导致网络拥塞、数据丢失等问题，传统的云计算已无法满足终端对高带宽、低时延和实时性的需求[1].

为了解决云计算的不足，新出现的网络计算模式在终端用户附近提供计算资源，并根据应用需求将数据就近处理[2]，如透明计算、cloudlet[3]、边缘计算、雾计算[4]和移动边缘计算等.cloudlet和雾计算的计算能力未集成到移动网络中，导致服务质量降低.移动边缘计算较其他计算模式更侧重于无线接入网络[5]，具有低时延、低能耗等优点.为了降低传输延迟，2014年欧洲电信标准协会提出移动边缘计算(mobile edge computing,MEC)，将延迟敏感的应用程序迁移到距离较近的边缘服务器(edge server,ES)进行计算与存储，并在2016年把MEC的概念扩展为“多接入边缘计算”(multi-access edge computing,MEC)，将MEC从电信蜂窝网络进一步延伸至其他无线接入网络(如WiFi).计算迁移是MEC研究的关键问题之一.终端根据实际应用场景指定不同的卸载策略时需考虑何时迁移、在何处迁移、如何迁移、迁移哪部分等，最终达到能耗与系统性能的平衡，提升用户的服务质量和体验质量.

目前，计算迁移算法性能优化目标主要集中在能耗、时延以及两者的联合优化.

1)以能耗为优化目标.文献[6]研究了基于非正交多址(non-orthogonal multiple access,NOMA)的节能多任务多址MEC，对任务计算卸载、本地计算资源分配和NOMA传输持续时间进行联合优化，以最小化终端完成所有任务的总能耗为目标.文献[7]研究了移动边缘计算迁移面临的可扩展性问题，提出一个轻量级的请求和准入框架解决可伸缩性问题，设计选择性迁移方案，最小化设备能耗.此外，文献[8-11]考虑不同的应用场景和约束，构建相应的优化模型，实现最小化能耗.

2)以时延为优化目标.文献[12]基于无人机群的三维分布构建了一个联合通信与计算优化模型，利用随机几何和排队论，实现了最优响应时延.文献[13]提出了一种低延迟的安全移动边缘计算系统，该系统优化用户的传输功率、计算容量分配和用户关联，在保证安全的资源约束条件下最小化用户计算和传输延迟.

3)以联合优化能耗和延迟为目标.文献[14]研究了物联网边缘云计算系统中的工作负载分配问题，基于时延和能耗约束设计智能算法，实现本地、边缘和云计算服务器的负载均衡.文献[15]定义能耗和时延之间折中的代价函数，提出了一种MEC辅助的计算和中继方案，获得移动设备和中继节点的最佳传输和压缩策略.另外，文献[16-20]针对不同场景下任务迁移的能耗与时延构建系统模型，平衡两者间关系，提升用户体验质量(quality of experience,QoE).文献[21]利用低秩矩阵理论与边缘计算去中心化的计算能力来处理大量交通数据，以实现精确和实时的恢复.

若将密集型任务迁移到一个ES时，当前ES由于达到负载阈值而无法完成，产生新的等待时延.根据分布式计算模式的特点，可将无法完成的任务迁移到相邻空闲的ES上进行计算，通过多个ES协作完成.因此，选择ES路径问题是关键.由于该问题为非凸优化问题，即NP难问题，与影响力最大化问题本质为同一问题.因此，可将ES路径择优问题转化为社会网络中影响力最大化问题.

针对社会网络影响力最大化问题，Kempe等人[22]首次提出运用贪心算法求解.随后，基于贪心策略改进的算法被大量提出.例如，利用影响力函数子模性的CELF(cost-effective lazy-forward)算法[23]、优化CELF算法后的CELF++算法[24]、将社会网络图缩小化后的NewGreedy算法[25]等.但贪心算法时间复杂度较高，无法适应于大型网络.因此，大量启发式算法被提出，最早的启发式算法是依据节点中心度来判断节点影响力大小[26].随后，基于度中心方法优化的DegreeDiscount算法[25]、利用K-shell算法的核覆盖算法(core covering algorithm,CCA)[27]、考虑邻居节点距离远近损耗的PageRank算法[28]、利用反向排名信息和邻居节点影响的逆向节点排名(reversed node ranking,RNR)算法[29]等相继被提出，有效解决了贪心算法时间开销较大等问题.其中，文献[27]提出的CCA算法充分考虑选取种子节点影响范围的重叠情况，基于K-shell分解求解出每个节点的核数，然后根据核数分布的层次性，引入节点的影响半径参数，最后综合核数和度数2个属性找出影响力节点集合.但启发式算法精准度较低，故有些研究者将2类算法相结合进行求解.例如，Chen等人[30]用最大影响力路径来估算影响力的传播，并提出了最大化影响力树状(maximum influence arborescence,MIA)算法进行求解该问题；Kim等人[31]结合贪心算法的精确度和启发式算法的高效率提出了独立路径算法(independent path algorithm,IPA)，通过设置阈值，将传播路径的概率近似为影响函数，缩短了运行时间.

本文将MEC计算迁移路径最优化转化为社会网络影响力最大化问题，充分考虑网络拓扑结构中ES的位置及属性，构建计算迁移路径优化选择算法，对不同ES通过K-shell算法进行分等级处理，有效减少ES路径搜索消耗成本.其核心思想是将ES类比为社会网络节点，通过K-shell算法定义ES路径影响力，提出K-shell影响力最大化计算迁移(K-shell influence maximization computation off-loading,Ks-IMCO)算法，有效降低能耗与时延，提高用户体验质量.

1 计算迁移系统建模与策略研究

假设由1个基站、n个边缘服务器和m个智能终端组成的移动边缘计算场景.n个ES共同构成网络G(P,E)，其中，P为边缘服务器构成的集合，P={pi|i=1,2,…,n}，E为边缘服务器连接矩阵.m个终端集合形式表示为D={dk|k=1,2,…,m}.终端dk的计算任务Rdk包括本地计算任务Rloc,dk和迁移计算任务Rtran,dk.如图1所示，终端与基站关联的ES通过正交频分复用(OFDMA)进行通信.

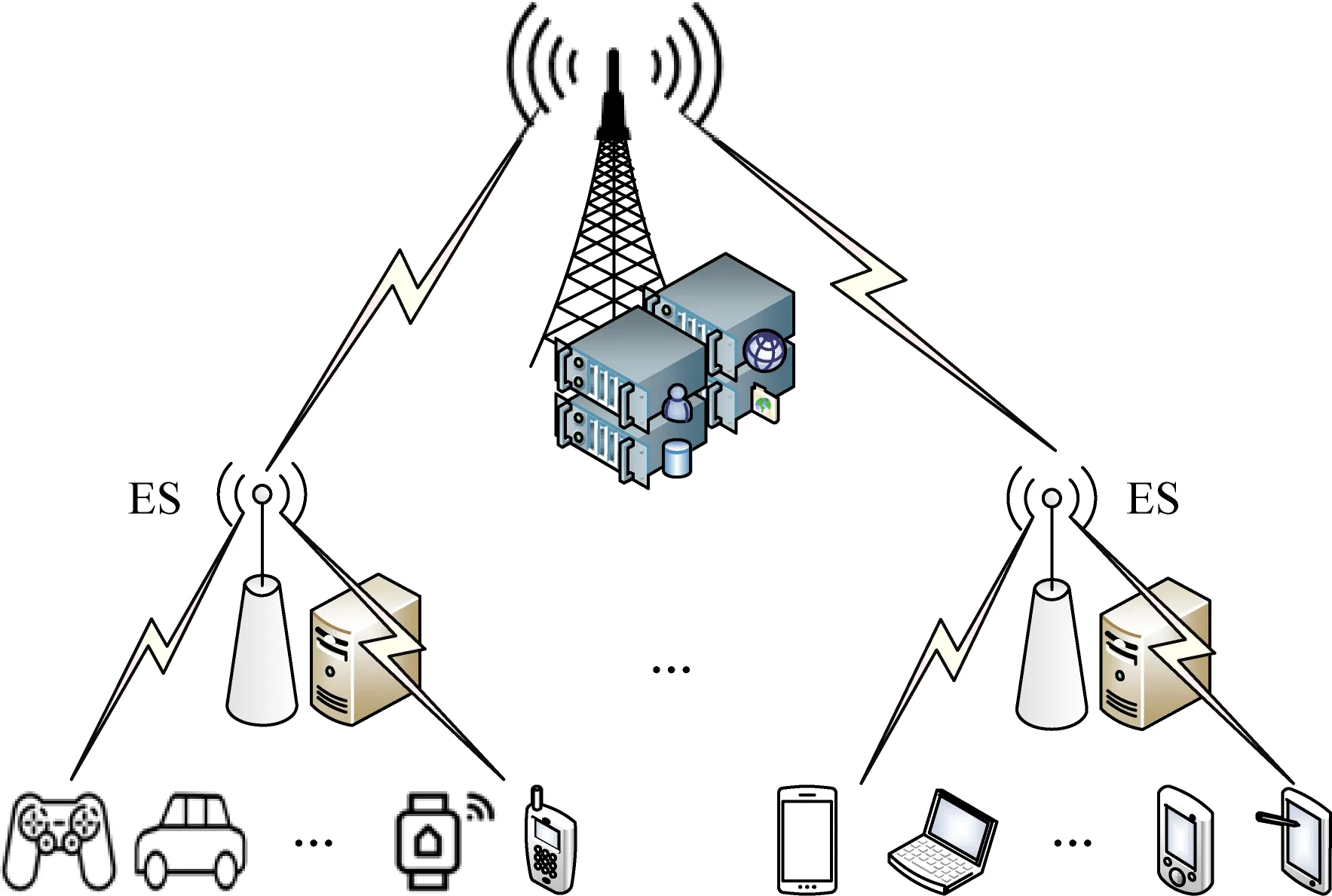
Fig.1 Multi-user mobile edge computing scenario图1 多用户移动边缘计算应用场景

考虑到终端计算能力受限，根据计算复杂度δk分割任务，dk在本地执行复杂度较低的任务，将复杂度高的任务迁移到ES执行.因此，使用二元变量δk∈{0,1}表示终端的决策，δk=0表示本地执行；δk=1表示迁移到ES执行，并将结果返回终端.计算迁移决策流程图如图2所示.

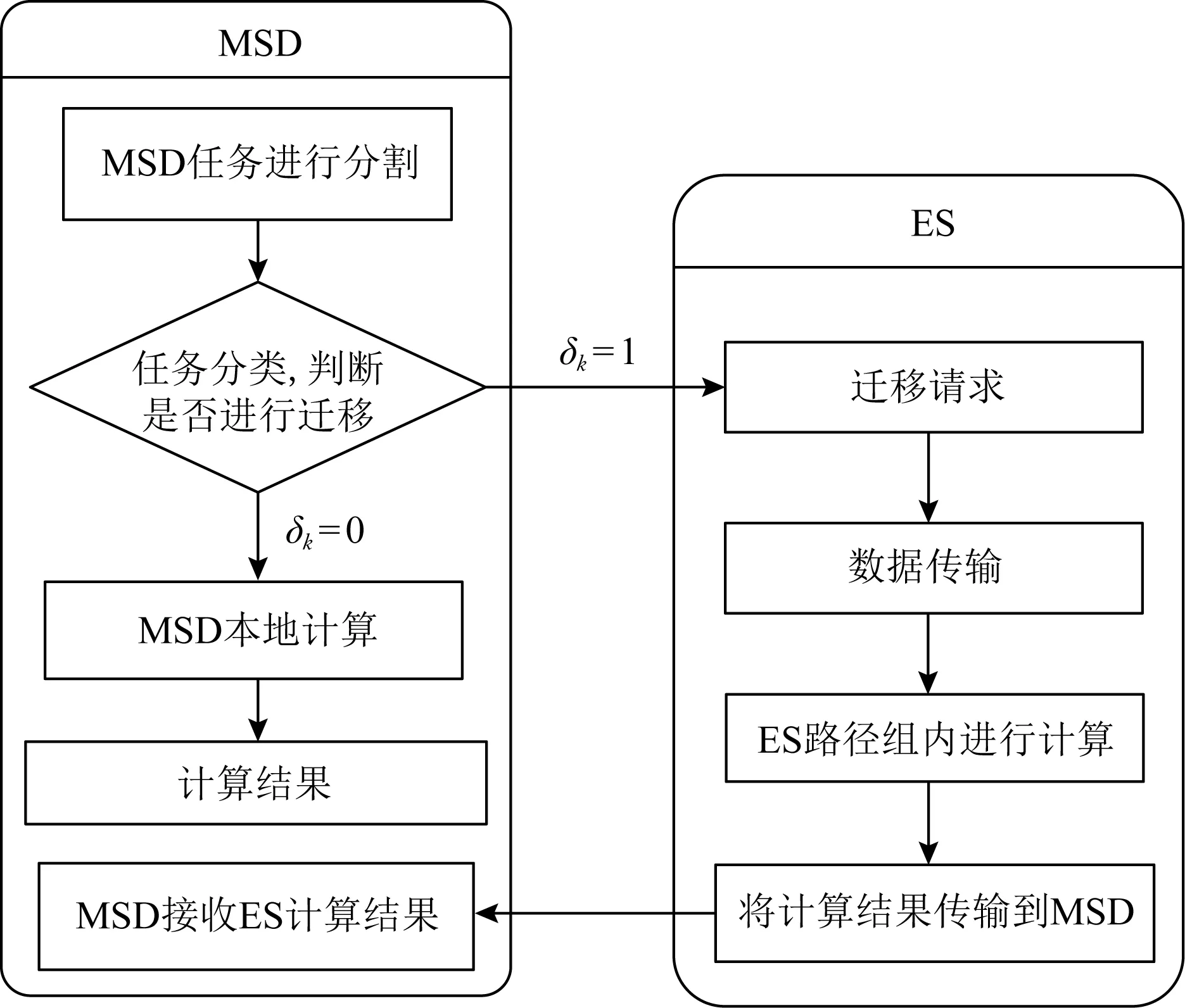
Fig.2 Computation offloading process[32]图2 计算迁移流程图[32]

1.1 任务本地计算建模与分析

在本地计算时，设终端dk分配的任务Rloc,dk运行功率为Ploc,dk，CPU频率为floc,dk，则本地计算所需时延Tloc,dk与能耗Eloc,dk可采用文献[33]中系统模型的构建思想表示为

(1)

(2)

由式(1)(2)得到本地服务质量公式Qloc,dk：

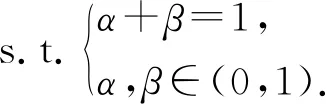
(3)

1.2 基于路径择优的计算迁移策略建模

为解决ES资源受限引起的多用户并发访问，导致网络堵塞.密集型任务模拟选择ES进行迁移，获得最佳迁移路线，即ES路径L′={p1,p2,…,pl}，其中l≤n.

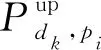
(4)

当前ES因资源受限无法完成终端dk迁移到边缘的任务Rtran,dk时，综合考虑计算任务在传输、计算过程中的时延与能耗，将部分任务迁移到相邻ES.其中计算任务的传输包括上行传输、边缘网络内传输和下行传输3部分.

迁移请求发起后，上行传输时延Tloc,mec、ES路径内传输时延Tmec,mec、下行传输时延Tmec,loc可分别表示为[13]：

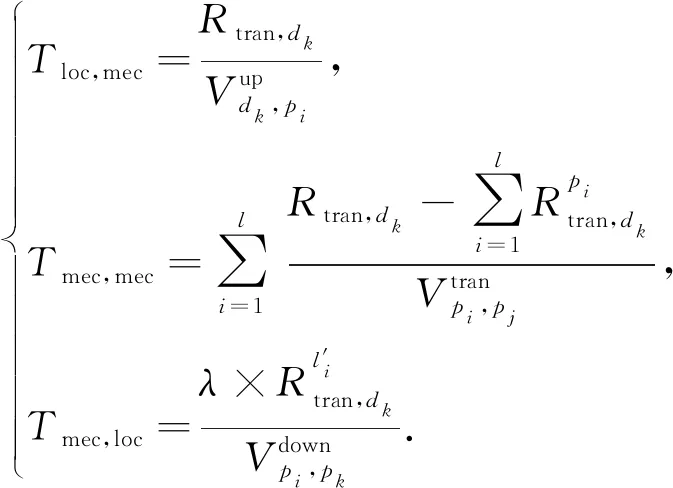
(5)

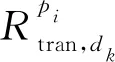
上行传输能耗Eloc,mec、ES路径内能耗Emec,mec、下行传输能耗Emec,loc分别为[15]：

(6)

根据式(5)(6)得到传输时延Ttran、传输能耗Etran分别为

Ttran=Tloc,mec+Tmec,mec+Tmec,loc，

(7)

Etran=Eloc,mec+Emec,mec+Emec,loc.

(8)

任务计算时，分别构建任务计算时延Tmec与计算能耗Emec模型[15]：

(9)

(10)

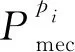
根据任务传输和计算开销，得到任务迁移计算所需要的时延Tcount,dk与能耗Ecount,dk分别为

Tcount,dk=Ttran+Tmec,

(11)

Ecount,dk=Etran+Emec.

(12)

由式(11)(12)得到迁移计算服务质量公式Qcount,dk：

Qcount,dk=αTcount,dk+βEcount,dk,

(13)

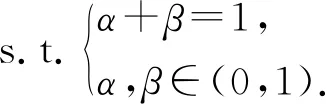
综上所述，任务迁移需要的总时延Ttotal,dk与总能耗Etotal,dk分别表示为

Ttotal,dk=Tloc,dk+Tcount,dk,

(14)

Etotal,dk=Eloc,dk+Ecount,dk.

(15)

由式(14)(15)得到任务迁移服务质量公式Qtotal,dk：

Qtotal,dk=αTtotal,dk+βEtotal,dk,

(16)

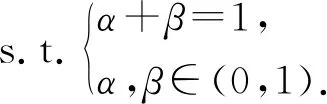
2 计算迁移路径选择优化策略

2.1 基于K-shell算法边缘服务器划分与计算迁移优化策略

在研究网络拓扑结构中，节点重要性度量方法常用指标有度中心性[34]、介数中心性[35]、紧密中心性[36]等.度中心性只关注了节点周围邻居数量，而介数中心性与紧密中心性需计算最短入境从而导致时间复杂度较高.文献[37]提出了节点重要程度依赖于所处网络中位置的思想，图论中经典的K-shell算法[38]充分利用了这一思想，能够准确有效地识别节点在网络中的影响力.

K-shell算法是通过层层剥离的方式对网络中节点进行分类.本文将网络中ES类比为节点，采用K-shell算法进行等级划分，通过网络拓扑结构区分ES在网络中的不同位置.假设网络内包含节点为a，b，…，q，r，如图3所示.具体分类过程为：

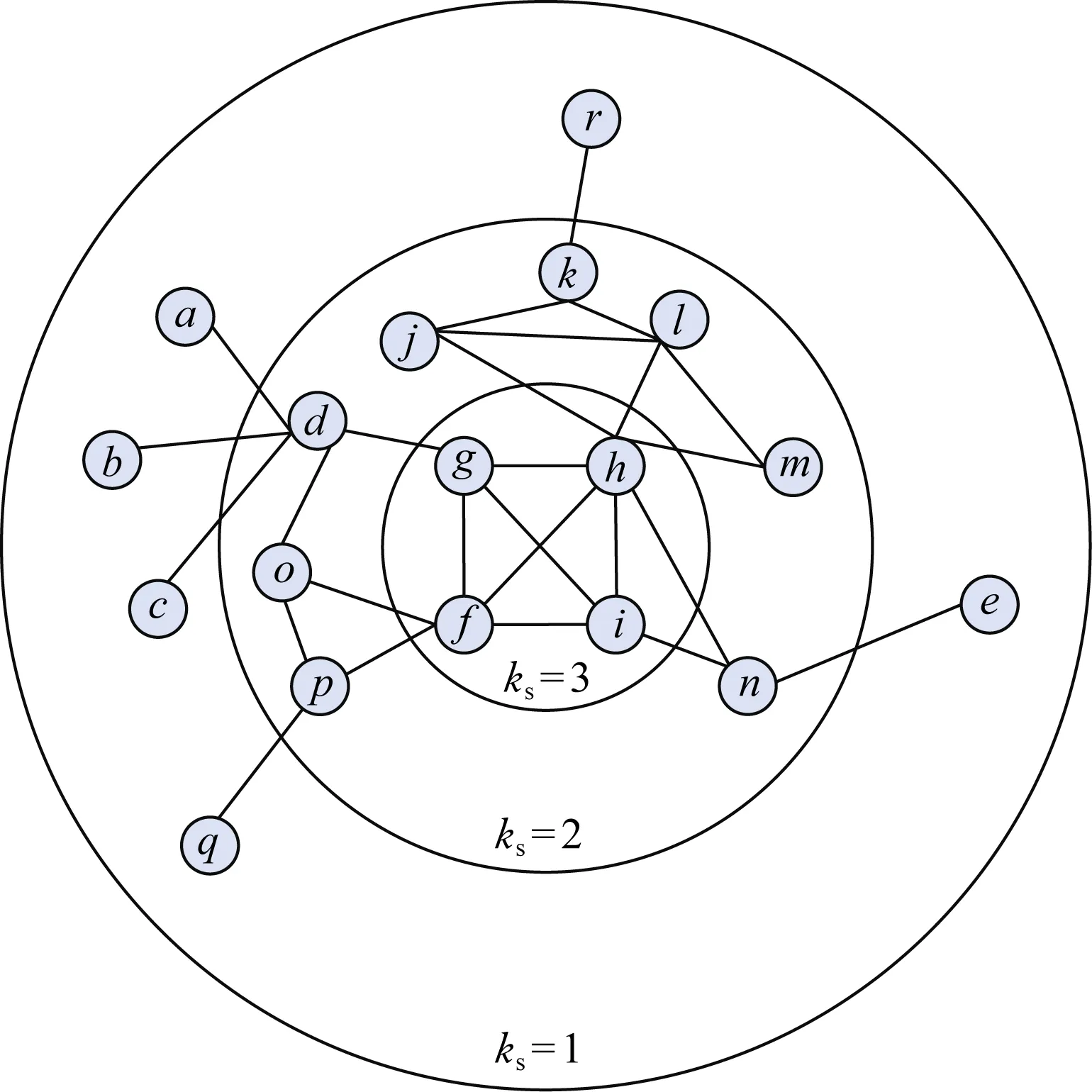
Fig.3 K-shell algorithm schematic[39]图3 K-shell算法示意图[39]

首先去除网络内度数最低(度数为1)的节点，即a，b，c，e，q，r标记ks=1；剩余的节点又会组成新的网络，此时度数最少的节点为d,o,p,n，m，l，k，j，这些节点的ks=2；以此类推，直到网络中所有的节点都具有ks值.

针对CCA算法[27]中所考虑种子节点间的覆盖范围重合的问题，结合本文研究问题，考虑任务传输过程中的路径重叠问题.由于该问题会导致边缘服务器负载过重，故构建路径重叠(path overlap,PO)算法.

算法1.路径重叠算法.

输入:ES网络G(P,E);

输出:路径集合S(L).

① for 每个ES

② 根据路径生成规则，查找所有迁移路径Lall；

③ end for

④ for 每个Lall

⑤ 搜索重叠路径；

⑥ end for

考虑ES计算能力、基站带宽资源、任务迁移时延与能耗因素，以用户体验质量(QoE)作为多终端迁移策略联合优化目标，构建近于实际应用环境的密集型任务系统模型minQ[11]：

(17)

式(17)为非凸优化问题，是一个NP难问题.针对NP难问题，以通信质量、ES交互频度等为约束，将其转化为影响力最大化问题用Ks-IMCO算法进行求解.

2.2 ES路径影响力选择模型

考虑到ES的计算、传输能力的差异性，构建ES路径对计算任务的评判标准：ES路径影响力.

ES路径影响力由其自身影响力与潜在影响力所构成.其中，ES自身影响力受ES在网络中所处位置与自身属性影响；潜在影响力主要考虑任务迁移时延、能耗和传输通信质量等.ES路径影响力选择模型过程如图4所示.

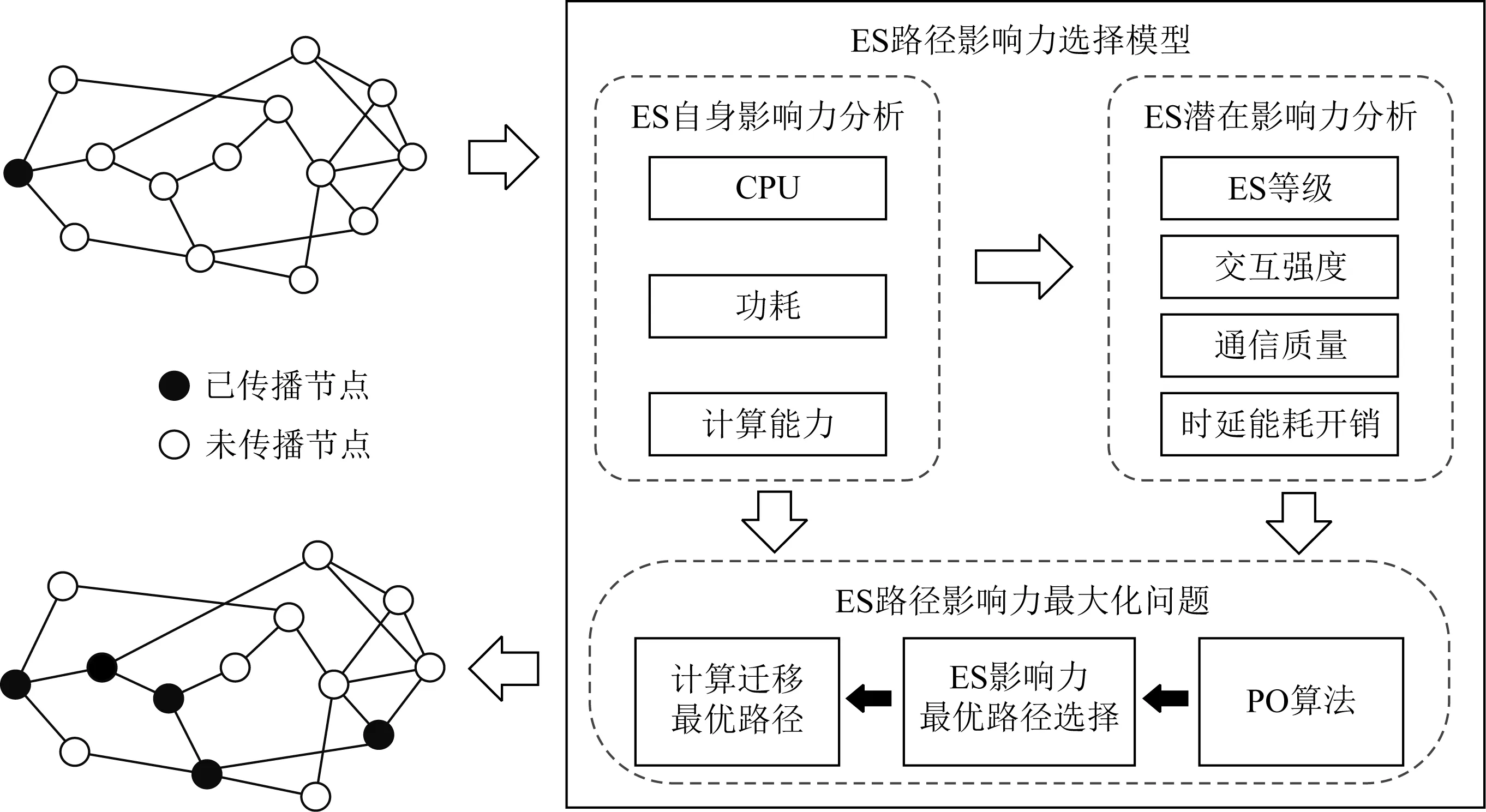
Fig.4 ES path influence selection model图4 ES路径影响力选择模型

综合考虑ES在网络拓扑结构所在位置，利用度中心方法度量ES重要性[26]：

(18)

(19)

潜在影响力表示ES路径具有的潜在计算能力，由K-shell方法计算；σ,Cqua分别表示ES之间的交互频度和通信质量；Ttotal,dk，Etotal,dk分别表示任务迁移延迟和能耗.则潜在影响力表达式为

(20)

σ∈(0,20],

其中，D(pi)为邻居节点pj的集合，ks为ES所处等级值，θ为随机分布变量，N0为噪声功率.

综上，ES路径影响力计算表示为

(21)

为了描述一致，将用户体验质量作为计算迁移策略优化目标转化为ES路径影响力最大化问题求解.则有：

(22)

证明.

由式(17)可得：

由式(22)可得：

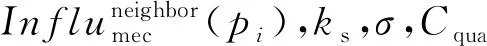
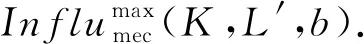
证毕.

2.3 Ks-IMCO路径寻优算法

根据ES所处ks等级，将备选迁移路径进行排队，迁移路径选择约束条件初始ES只能向同级或低级延伸.算法描述为：

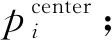
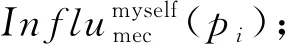
步骤3.计算ES的ks；

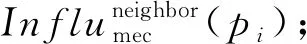
步骤6.运行PO算法，对路径重叠部分选择其影响力最大路径进行计算迁移；

步骤7.得到最终计算迁移路径.

算法2.K-shell影响力最大化计算迁移算法.

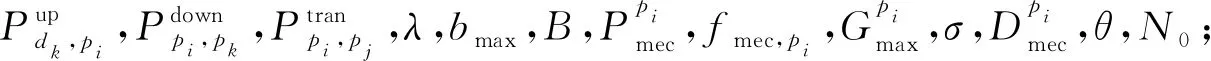
输出:路径集合S(L′).

① for 每个ES

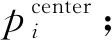
④ 计算pi(ks)；

⑤ 根据路径生成规则，查找所有迁移路径

⑥ end for

⑦ for 每个MSD任务Rdk

⑧ ifδk=0

⑨Rloc,dk执行本地计算；

⑩ else ifδk=1

Eloc,dk；

与能耗Ecount,dk；

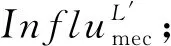
3 仿真实验与分析

3.1 仿真实验设计

一个社区由多个MSD与ES构成，每个MSD与ES通过正交频分复用(OFDMA)信道相连，各个信道之间相互独立.在同一时刻，每个MSD将计算不同大小的任务，按照计算复杂度策略将任务进行分割，对于密集型任务通过信道进行计算迁移，完成多用户多服务器的边缘计算.具体仿真参数如表1所示：

Table 1 Simulation Parameter表1 仿真参数

3.2 算法仿真与性能分析

实验1.本地计算与Ks-IMCO算法迁移计算能耗对比分析.

本地计算迁移策略与Ks-IMCO算法迁移计算进行对比分析，实验过程中，将每个MSD任务随机设为10～100 GB，在500个ES组成的数据集进行仿真，观察MSD数目由0～500过程中能耗所发生的变化.Ks-IMCO算法迁移计算能耗仅计算MSD分割后任务的本地计算能耗与上传能耗，实验结果如图5、图6所示:

Fig.5 Comparison of energy consumption betweenKs-IMCO offloading calculation and local calculation图5 Ks-IMCO迁移计算与本地计算的能耗对比

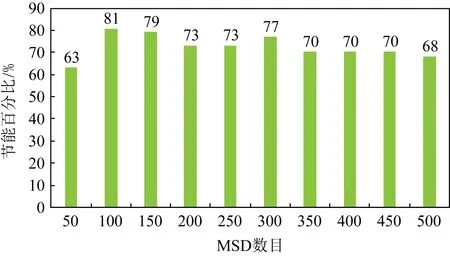
Fig.6 The percentage of MSD energy saving calculated by Ks-IMCO algorithm offloading图6 Ks-IMCO算法迁移计算的MSD节能百分比

从图5、图6可以看出，当系统MSD数目在100时，Ks-IMCO迁移计算能耗降低80%以上；系统MSD数目在100～450时，Ks-IMCO迁移计算能耗降低70%以上；当系统MSD数目在350～450时，Ks-IMCO算法迁移计算节能效果趋于稳定，维持在70%左右.Ks-IMCO算法迁移计算能耗明显小于本地计算.

实验2.不同算法能耗与时延对比分析.

将Ks-IMCO算法分别与随机分配(random allocation,RA)、路径选择切换(path selection with handovers,PSwH)算法[20]对比分析其有效性.

设Rdk为MSD计算任务量.不同数量级的任务量代表不同格式文件，具体划分如表2所示：

Table 2 Task Volume Division表2 任务量划分

针对Ks-IMCO算法与RA算法、PSwH算法分别在不同场景下进行时延与能耗对比实验，实验过程中逐渐增加MSD数目观察时延与能耗性能.为了提高实验的准确性，针对ES网络规模，分别以500，1 000，2 000，5 000的数据集进行实验.

纯文本文件实验结果如图7～10所示:

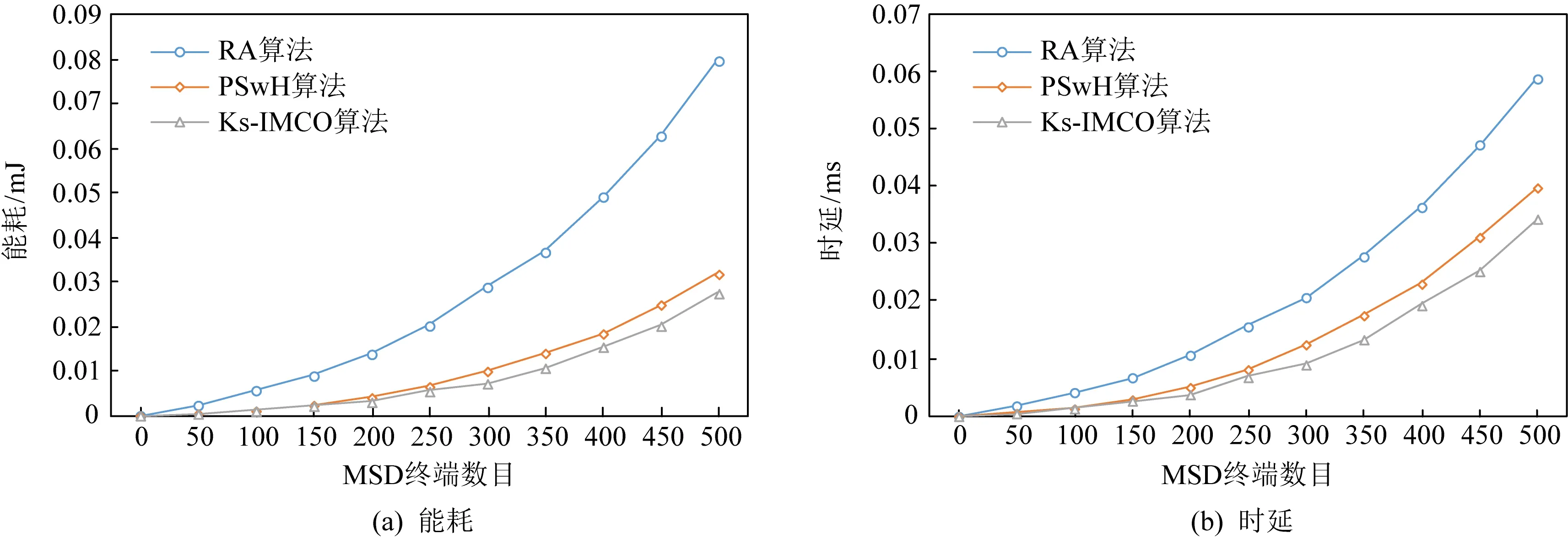
Fig.7 A network of 500 ES terminals for text files task图7 500个ES终端组成的网络完成纯文本任务

Fig.8 A network of 1 000 ES terminals for text files task图8 1 000个ES终端组成的网络完成纯文本任务

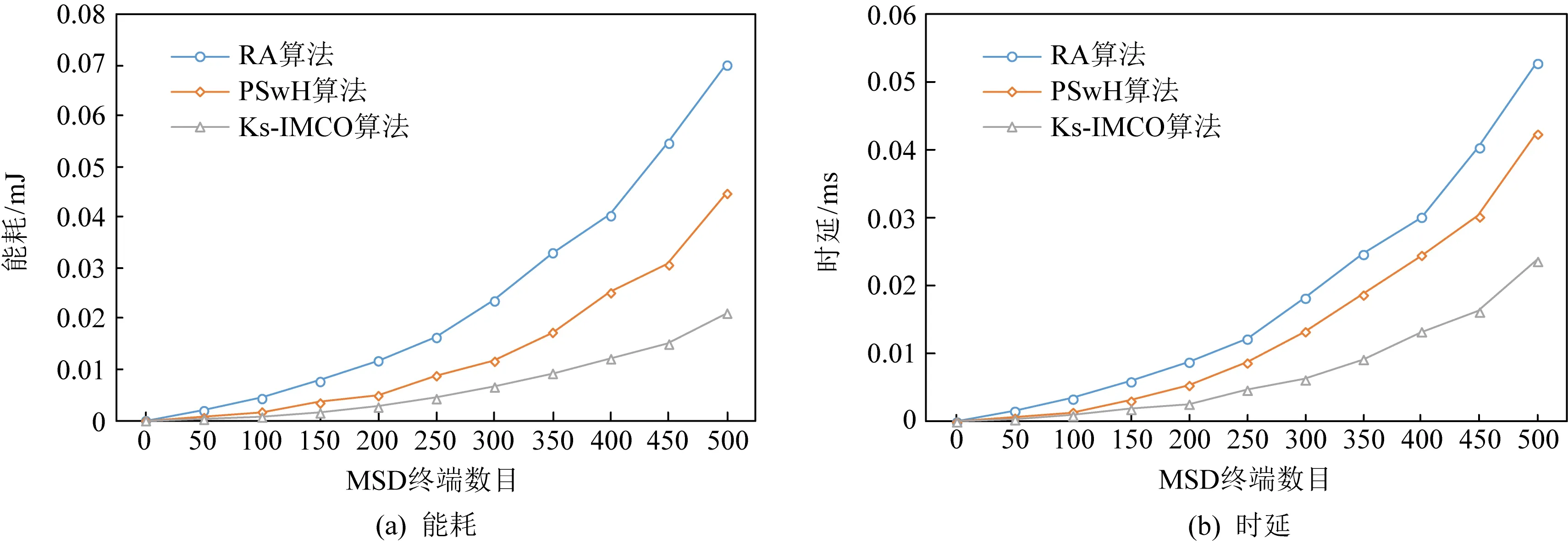
Fig.9 A network of 2 000 ES terminals for text files task图9 2 000个ES终端组成的网络完成纯文本任务

Fig.10 A network of 5 000 ES terminals for text files task图10 5 000个ES终端组成的网络完成纯文本任务

图片文件实验结果如图11～14所示.

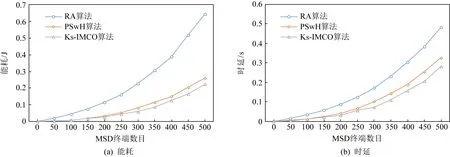
Fig.11 A network of 500 ES terminals for picture files task图11 500个ES终端组成的网络完成图片文件任务

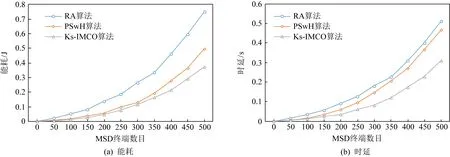
Fig.12 A network of 1 000 ES terminals for picture files task图12 1 000个ES终端组成的网络完成图片文件任务

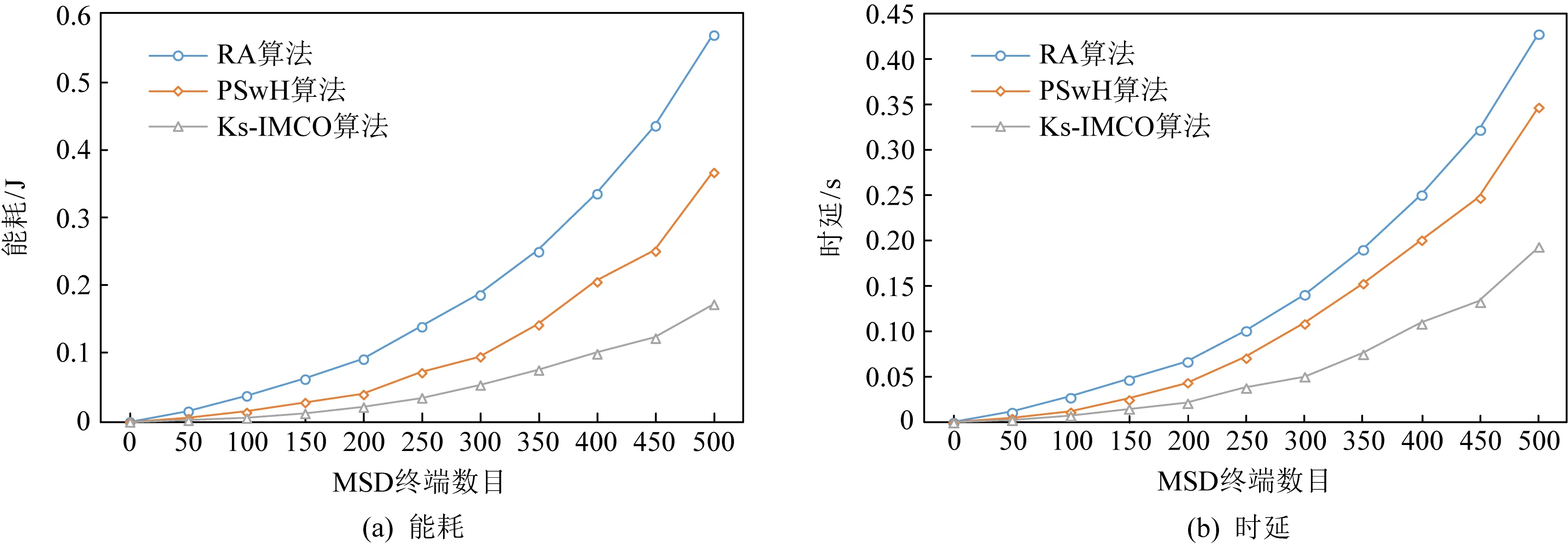
Fig.13 A network of 2 000 ES terminals for picture files task图13 2 000个ES终端组成的网络完成图片文件任务

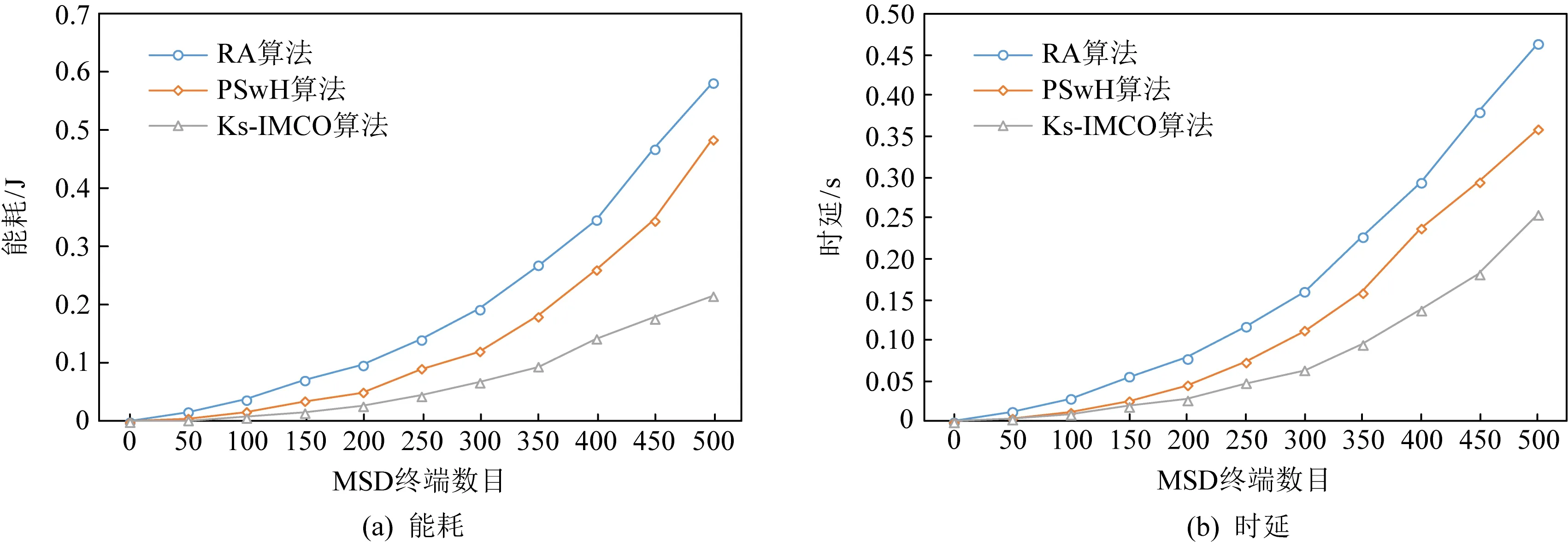
Fig.14 A network of 5 000 ES terminals for picture files task图14 5 000个ES终端组成的网络完成图片文件任务

流式文件实验结果如图15～18所示.

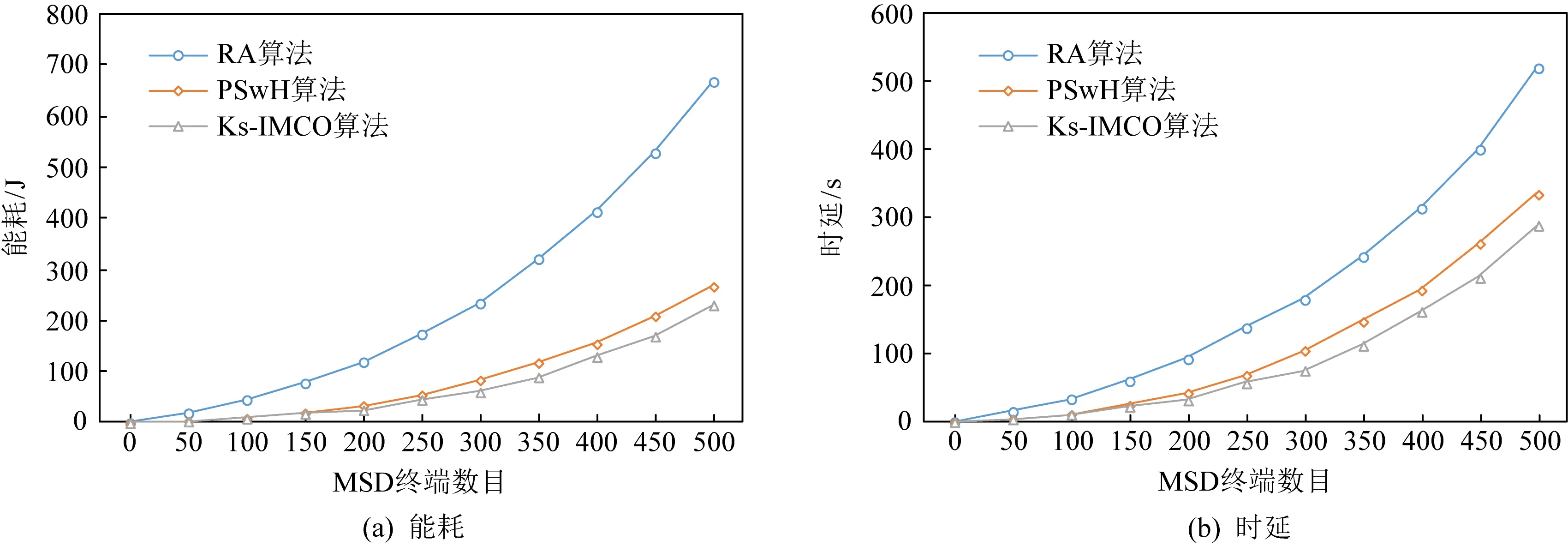
Fig.15 A network of 500 ES terminals for streaming files task图15 500个ES终端组成的网络完成流式文件任务

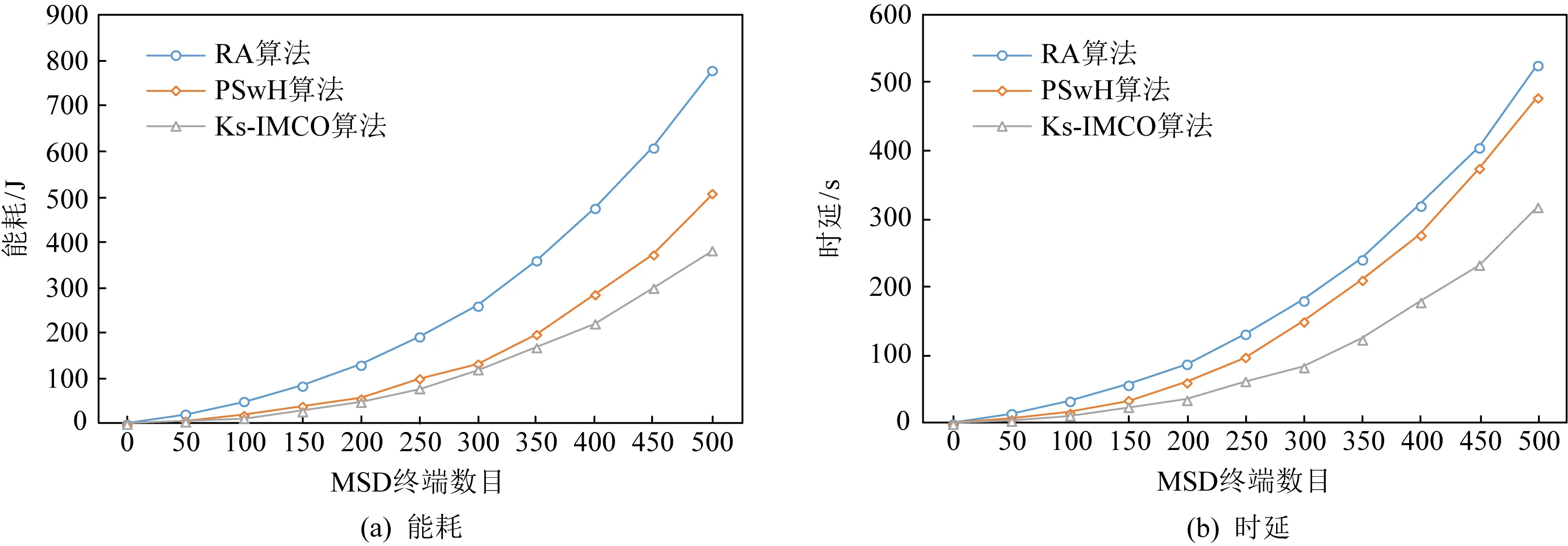
Fig.16 A network of 1 000 ES terminals for streaming files task图16 1 000个ES终端组成的网络完成流式文件任务

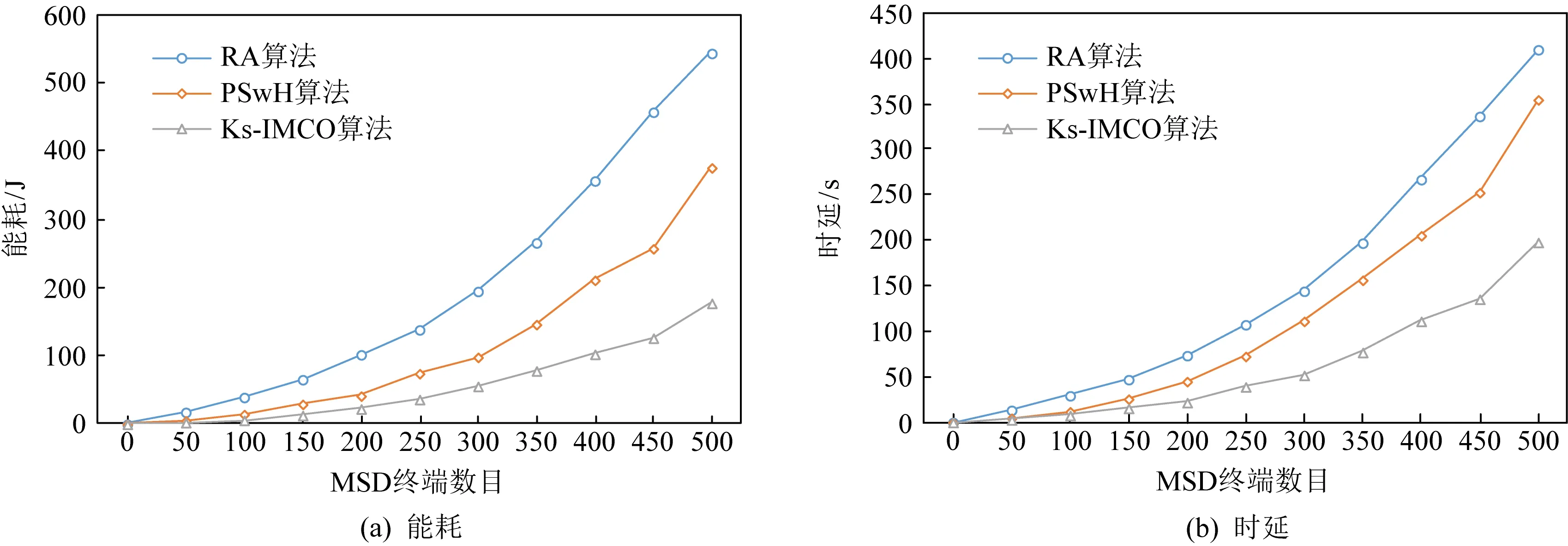
Fig.17 A network of 2 000 ES terminals for streaming files task图17 2 000个ES终端组成的网络完成流式文件任务

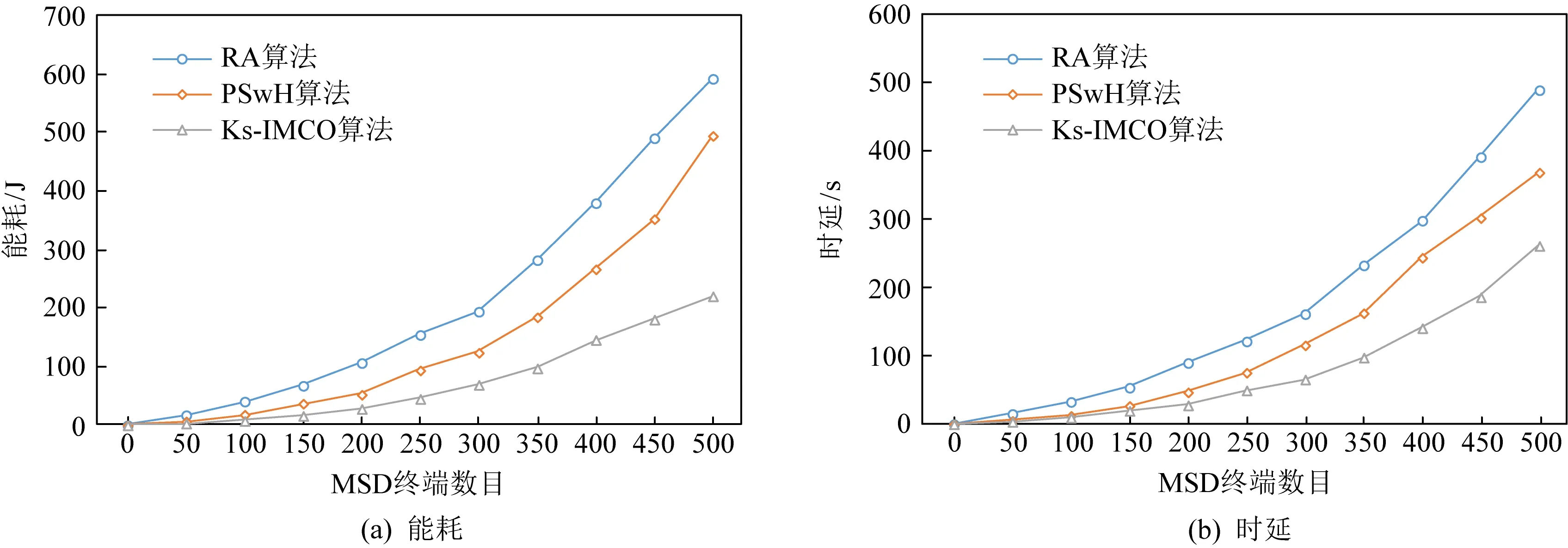
Fig.18 A network of 5 000 ES terminals for streaming files task图18 5 000个ES终端组成的网络完成流式文件任务

大规模数据流式文件实验如图19～22所示.

Fig.19 A network of 500 ES terminals for large-scale data streaming files task图19 500个ES终端组成的网络完成大规模数据流式文件任务

Fig.20 A network of 1 000 ES terminals for large-scale data streaming files task图20 1 000个ES终端组成的网络完成大规模数据流式文件任务

Fig.21 A network of 2 000 ES terminals for large-scale data streaming files task图21 2 000个ES终端组成的网络完成大规模数据流式文件任务

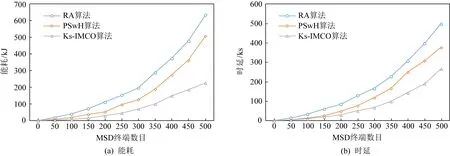
Fig.22 A network of 5 000 ES terminals for large-scale data streaming files task图22 5 000个ES终端组成的网络完成大规模数据流式文件任务

从表3可以看出，对于不同形式的任务Rdk，当ES规模为500且MSD数目为500时，Ks-IMCO算法较RA算法节能60%～70%，时延缩短41%～48%，较PSwH算法节能13%～15%，时延缩短12%～15%；当ES规模为500且MSD数目为1 000时，Ks-IMCO算法较RA算法节能45%～55%，时延缩短35%～40%，较PSwH算法节能24%～26%，时延缩短30%～36%；当ES规模为500且MSD数目为2 000时，Ks-IMCO算法较RA算法节能65%～70%，时延缩短43%～55%，较PSwH算法节能40%～55%，时延缩短38%～47%；当ES规模为5 000，MSD数目为500时，Ks-IMCO算法较RA算法节能60%～65%，时延缩短45%～50%，较PSwH算法节能55%～57%，时延缩短24%～38%.随着ES规模逐渐增大，Ks-IMCO算法对比RA算法节能总体维持在60%左右，对比PSwH算法节能逐渐增高；Ks-IMCO算法对比RA，PSwH算法具有较短时延.因此，从能耗与时延方面看，Ks-IMCO算法能有效提高用户服务质量.

Table 3 Algorithm Comparison when Task is Streaming File and ES Number is 500表3 任务为流式文件、ES数目为500的算法对比

4 讨论问题与未来工作

对于边缘计算中能耗与时延优化问题影响因素不仅在于路径的选择问题，其中也包含在路径选择前的任务分配、ES路径分布重叠稀疏度问题.

1)任务分配对路径选择以及能耗和时延的影响.由于本文中对于任务分配进行主动划分，故在进行计算迁移时，任务进行迁移或在本地计算时可能对路径选择以及能耗和时延产生影响.为此，我们进行随机实验对比分析，为使实验效果最为明显，选取MSD任务为10～100 GB范围内进行实验.实验结果如图23所示，从图23(a)中可看出主动划分时延小于随机划分，图23(b)中可看出主动划分能耗小于随机划分.在今后的工作中，将研究如何进行任务智能划分，对不同终端发布任务根据任务量以及可迁移路线进行智能划分，进一步优化迁移计算能耗与时延.

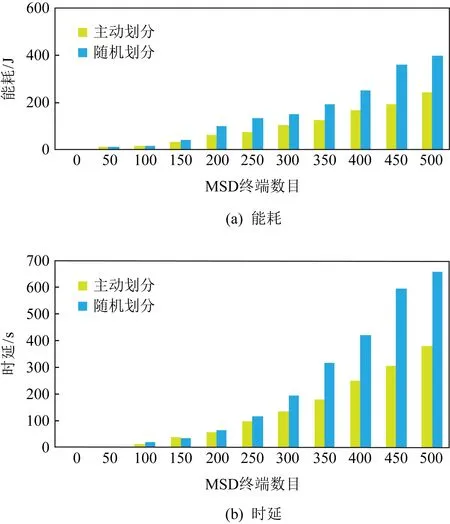
Fig.23 The influence of task assignment on energy consumption and delay图23 任务分配对能耗和时延的影响

2)ES路径分布重叠稀疏度对路径选择以及能耗和时延的影响.通过选取不同稀疏的ES路径分布进行实验结果如图24所示.从图24(a)中可以看出对于稀疏度高的ES路径分布图能耗与稀疏度低的ES路径分布图相差无几,图24(b)中可以看出对于稀疏度高的ES路径分布图时延小于稀疏度低的ES路径分布图.

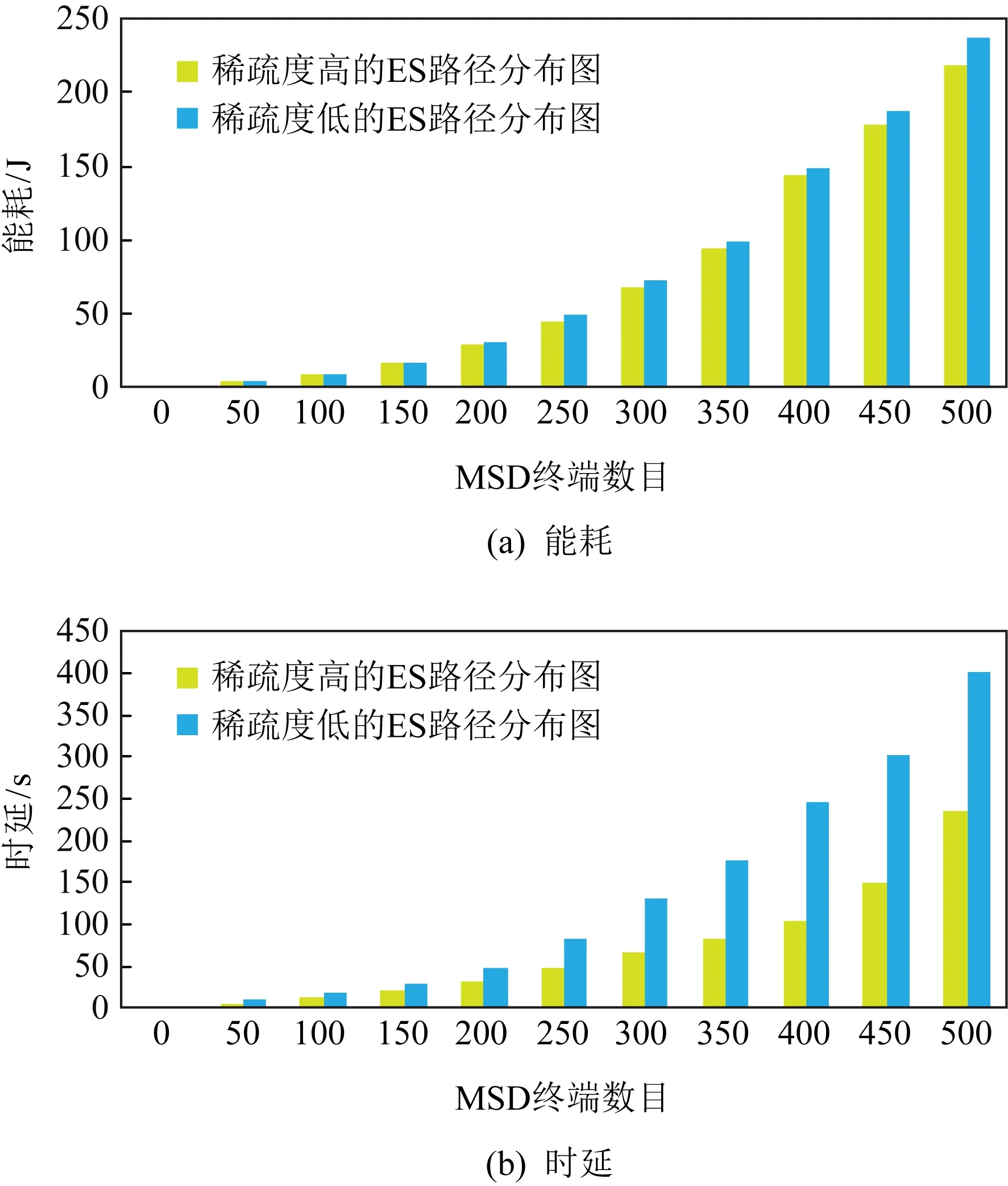
Fig.24 The influence of ES path distribution overlap and sparsity on energy consumption and delay图24 ES路径分布重叠稀疏度对能耗和时延的影响

5 总 结

本文将边缘计算中计算迁移路径选择问题转化为社会网络影响力最大化问题，为计算迁移路径择优问题提供了新思路，将问题转换可以有效利用网络拓扑结构进行边缘服务器分层，节约路径搜寻时间，依据社会网络影响力最大化问题中的K-shell算法进行路径影响力定义，提出了Ks-IMCO算法求解该问题.实验结果表明：Ks-IMCO算法迁移计算较本地计算能耗有效节能在70%左右；对于不同形式的任务，Ks-IMCO算法在能耗与时延方面都优于RA，PSwH算法.