量子优化算法综述

何键浩 李绿周

(中山大学计算机学院 广州 510006)

优化(optimization)是计算机科学与数学领域十分重要的基础研究之一，同时也是机器学习的核心工具[1].相关理论与方法广泛应用于各类工业生产[2]、工程设计与管理[3-5]、交通运输[6]、经济决策[7]、市场管理[8]等关乎国计民生的重要领域.一个具体的优化问题由3个基本要素组成：1)目标函数(或损失函数)，即决策者需要优化的指标，如总消耗、总收益等，数学形式表现为由优化变量到指标的函数/映射.2)优化变量，即决策者可以调整且会影响到目标函数的变量，如产品工艺、资金分配等.3)约束条件，即在决策过程中必须遵守的限制，如安全标准、资源储备总量等.优化过程就是在约束条件的限制下，寻找能最小化或最大化目标函数的优化变量的赋值.优化有时候也被称为数学规划，下文中优化与规划意义等价，具体使用的词汇将根据该细分方向的用词习惯决定.

根据优化问题的变量是否连续，优化技术可以分为离散变量优化(也称为组合优化)和连续变量优化两大类.其中，根据目标函数是否是凸的，连续变量优化又可分为凸优化和非凸优化.凸优化主要研究的是目标函数为凸函数且优化变量可行域为凸集的优化问题，由于凸集凸函数有许多优秀的性质(例如极小值即最小值)，使得凸优化问题有很多高效的解法，在应用迭代方法求解时也能获得良好的收敛速度.因此，凸优化技术方面已有成体系的方法且有广泛的应用.相对而言，非凸优化还有很大的发展空间.另外，许多非凸优化问题，目前有效的办法仍然是转化为凸优化问题求解.

与此同时，自从Shor快速整数分解量子算法[9]、Grover量子搜索算法[10]以及HHL量子解线性方程算法[11]的提出，量子计算就因其与生俱来的并行性而受到广泛关注，近年来量子计算理论方面的研究进展可参考文献[12-13].因此，如何利用量子计算技术来加速优化问题的求解、提高优化效果成为受关注的问题，逐渐形成了量子优化这一研究方向.量子优化算法的研究从时间上大致分为1996—2015年和2015—2021年这2个阶段.

1)1996—2015年.此阶段的量子优化算法主要是针对离散变量优化问题而设计，且有较多的启发式算法.此阶段的量子算法主要得益于当时3类基础离散量子技术：

① Grover算法以及量子随机游走.这2个基础算法后续还有不少改进与扩展，多被用于加速搜索过程.

② 量子退火法.量子退火法无需使用纠缠态，实现较简单，因此已经有了D-Wave这样的大型专用量子计算机可供实验研究.

③ 量子近似优化技术.量子近似优化算法虽然还没有关于理论优势的严格分析，但被认为适合近期的含噪中等规模量子(noisy intermediate-scale quantum,NISQ)计算设备，因此得到不少关注.

2)2015—2021年.此阶段的量子优化算法主要针对连续变量优化问题而设计.连续变量优化问题的解法以迭代算法为主，迭代开销以及收敛速度是影响算法效率的主要因素.此阶段的量子算法主要得益于4类量子技术的发展：

① 解线性方程量子算法的设计思想.此类方法可用于加速与矩阵操作相关问题的求解.

② 哈密顿模拟技术.此类方法的发展为量子态演化提供了高效的实现方案.

③ 量子随机存储器.借助量子随机存储技术对数据进行预处理，可以使算法的效率得到提升，不过量子随机存储的搭建仍然需要进一步的优化来保证整体的优势.

④ 量子梯度估计法.计算梯度是许多优化问题的核心步骤，量子梯度估计法的提出为此提供了便利.

连续变量量子优化算法是近年的研究趋势，研究内容涵盖了优化领域中梯度下降、牛顿法、内点法等常用的传统迭代方法，也有针对具体优化问题的持续研究，因此本文将重点介绍连续变量量子优化算法，该方向的研究目前主要集中在量子凸优化方面.

1 基本量子算法简介

本节介绍在量子优化算法中使用频率较高的基本量子算法/技术.关于量子计算的基本知识以及更全面的介绍可参考文献[14-16].本节主要介绍一些相对底层的核心算法/技术，它们最初设计时并不是为了优化算法，可广泛应用于不同的领域，其中当然也包括优化领域.

1.1 Grover算法与量子随机游走(Grover algorithm &quantum random walk)

Grover算法与量子随机游走已经被应用在许多领域，其中就有离散优化领域.Grover算法于1996年被提出[10]，用于无序数据库搜索，其方法是通过迭代利用一个可识别搜索目标的黑盒来提高搜索目标在量子叠加态中的振幅，从而提高测量获得搜索目标的概率.后续有多个相关的改进结果，如由清华大学的Long提出的Grover算法的精确版本[17].原始的Grover算法需要确切知道搜索空间中目标的数量才能确定最优的迭代次数，过少的迭代次数达不到效果，过多的迭代也会降低搜索的成功率，迭代次数增多并不能保证一直趋向搜索目标.该问题在文献[18]中被称为“soufflé problem”.因此，对于搜索空间中目标数量未知的情形，算法需要改进，Grover和Mizel先后对此作过讨论，并给出了随着迭代次数增加能一直增加搜索成功率的改进版本[19-21]，但这几项工作都一定程度上牺牲了算法效率.最终Yoder等人给出了进一步改进[22]，既保留了平方加速，也保证了迭代最终会一直趋向搜索目标.此系列改进工作被称为固定点量子搜索(fixed-point quantum search).若搜索前对答案有一定的先验知识，He等人给出了相应最优算法[23].

量子随机游走于1993年由新墨西哥大学的Aharonov等3名学者提出[24].不同时期量子随机游走的工作梳理可参见文献[25-28].Grover算法可以看作是在一种特殊图上的量子随机游走，因此量子随机游走是一种更一般化的量子搜索技术，已经成为一类重要的量子算法设计模型.

1.2 量子傅里叶变换与量子相位估计算法(quantum Fourier transform &quantum phase estimation algorithm)

作为量子算法里提供加速的最为核心的2个基本工具，量子傅里叶变换最早可追溯到1994年[29]，而量子相位估计算法最早可追溯到1995年[30].利用量子解线性方程思想以及量子梯度估计法的量子优化算法都直接或间接地使用了量子傅里叶变换或量子相位估计算法.读者可以在任一量子计算教材中找到这2个基本工具的详细介绍[14-16].

1.3 量子幅值放大/幅值估计(quantum amplitude amp-lification and amplitude estimation)

2002年，Brassard等4名学者提出了量子振幅放大以及量子振幅估计算法[31].前者通过一系列的反射操作，达到放大所需结果概率的目的;而后者则是在前者的基础上结合量子相位估计算法，从而估计所需结果的概率.在量子优化算法中，不完美的演化产生的垃圾信息，以及算法本身产生的无用信息一般都通过振幅放大过滤掉.该工作与Grover算法[10]以及量子计数[32]有密切联系.Ambainis于2012年提出了量子振幅放大算法的时变版本[33]，并用于求解线性代数问题.量子振幅估计算法近期还有针对非布尔函数的推广[34]以及无需使用量子相位估计算法的变种[35].

1.4 解线性方程量子算法(quantum linear system algorithm)

解线性方程量子算法最早在2009年由Harrow，Hassidim，Lloyd三名学者提出[11]，所以也被称为HHL算法.解线性方程即给定矩阵A与向量b，求满足Ax=b的x.此类算法也可以用来处理矩阵与向量乘积、矩阵求逆等操作，因此也常见于量子优化技术的迭代算法中.需要注意的是，解线性方程量子算法求解的是量子版本的问题，即输入输出均为量子态，无法直接得到解的每一个分量，因此在进一步应用时需要经过巧妙设计，一般在利用方程解的全局信息时才能体现量子算法的加速效果.Ambainis于次年提出了改进版本，减少了算法复杂度对矩阵条件数的依赖[36].2017年，Childs等3名学者用其他思路给出了解线性方程量子算法[37]，减少了计算复杂度中对精度的依赖.2018年，Wossnig等3名学者利用量子奇异值估计算法，去除了计算复杂度中对矩阵稀疏度的依赖[38].关于此系列工作的梳理可以参见文献[39].

1.5 量子随机存取存储(quantum random access memory)

要在经典问题上使用量子算法，经典数据编码成量子态是必不可少的重要步骤，量子随机存取存储(简称QRAM)则是这一过程的主要辅助技术.同为实现数据的存储和提取，QRAM与经典的随机存储器最大的区别是：QRAM可以被量子叠加态地址访问，返回与地址相纠缠的叠加态数据，这为量子优化算法以及量子机器学习的初态制备提供了有力工具.在量子优化中使用得较多的为2008年Lloyd等3名学者提出的Bucket-Brigade结构的QRAM[40-41]，利用此结构在对数时间复杂度内可实现初态制备.值得注意的是搭建QRAM的时间复杂性仍然较高，整体上会抵消掉量子算法带来的加速，QRAM搭建技术仍然需要进一步优化.2018年，Chakraborty等3名学者提出了块编码技术，并证明与Bucket-Brigade结构在矩阵编码上等价[42].

1.6 哈密顿量模拟(Hamiltonian simulation)

哈密顿量是与量子系统总能量有关的运算符，根据薛定谔方程可知，它可用于描述量子系统随时间的演化，通过操作哈密顿量可以实现量子态的演化.在部分量子优化算法中(特别是用到解线性方程量子算法思想的算法)，矩阵被编码成哈密顿量的形式，进而作用到量子态上.哈密顿量模拟就是寻找能高效逼近目标哈密顿演化的酉演化，从而在有效时间内完成演化(亦即实现了量子算法的过程).关于哈密顿量模拟的正式结果最早可追溯到1996年Lloyd发表在《Science》上的文章[43]，并随后被推广到稀疏哈密顿量的模拟上[44-45]，且效率得到逐步提升[46-49].以上的工作针对的都是时间无关哈密顿量，而其后还有针对时间相关哈密顿量的推广工作[50-51].除研究时间复杂度与查询复杂度外，近年也出现了研究哈密顿量模拟采样复杂度的工作[52].

2 离散变量量子优化技术

本节简要介绍离散变量量子优化技术.主要离散变量量子优化技术的提出时间距今较长，因此本节只简单介绍各技术的历史以及给出重要工作的引文供读者进一步了解.

2.1 基于Grover算法与量子随机游走的优化算法(optimization based on Grover algorithm &quantum random walk)

经典离散优化的算法往往离不开搜索，而Grover算法与量子随机游走则正是加速搜索的量子算法，因此十分适合用于加速离散优化问题的求解.用Grover算法解决的离散优化问题有：无序数据最小值寻找[53]、最小生成树与最短路问题[54]、最大整数网络流查找[55]等.作为Grover算法推广的振幅放大算法也有相应的离散优化应用[56].量子随机游走则被用于加速基于Markov链的技术[57]等.近年也有用连续时间量子随机游走解决组合优化问题的工作[58].

2.2 量子退火/量子随机优化(quantum annealing/quantum stochastic optimization)

量子退火法于1989年由比勒费尔德大学的Carvalho等3位学者提出[59]，也称为量子随机优化.如遗传算法、蚁群算法与模拟退火等仿生算法都是非常实用的启发式优化技术，其中模拟退火法是出现得较早的经典技术，研究较深入.1)量子退火法中使用隧道场强度作为经典模拟退火法的温度参数.由于量子隧穿效应的存在，使得量子退火法更容易跳出局部最优解，获得全局最优解，从而体现出超越经典模拟退火的优势.2)量子退火不需要运用量子纠缠，因此易于实现，D-Wave公司生产的专用量子计算机即可运行量子退火算法.关于量子退火的早期工作可参阅文献[60-61]，关于D-Wave计算机与量子退火的综合介绍可参阅文献[62].

2.3 量子近似优化算法(quantum approximate optimization algorithm)

一般我们说的量子近似优化算法，都习惯特指本节所述的求解组合优化问题的量子近似优化算法，关于该算法的入门介绍可参照文献[63-64].

量子近似优化算法(简称QAOA)于2014年由麻省理工学院的Farhi等3位学者提出[65]，最初的设计是用于求解组合优化问题.该工作的量子电路深度依赖于一个与精度有关的参数，最坏情况下电路深度随着该参数与约束条件数量的乘积呈线性增长.该工作给出了使用QAOA解决p-正则图最大割(Max-Cut)问题的例子(p≤3)，而传统做法是把最大割问题转化为圆锥线性优化问题(conic linear optimization problem)解决.相较于经典算法，初期的QAOA并没有显示出明显的优势，直到2016年麻省理工学院的Harrow等2名学者指出QAOA是实现量子霸权(quantum supremacy)的方法之一[66]，热度才有所上升，近年也有理论分析的尝试[67].另一方面，QAOA算法实现时对相干时长要求低，或许是现有的小规模量子计算机理想的实验内容之一，因此受到了量子计算实验研究者的关注，陆续有实验文章出现[68].另外，近年也出现了用QAOA算法解决连续优化问题的研究，见3.5节.

3 连续变量量子优化技术

本节将详细介绍连续变量量子优化技术.连续变量量子优化技术是近5年的研究热点，因此本节将详细给出各工作所针对的具体问题、算法复杂度，以及所采用技术的直观描述.对于与经典模型有关的量子算法，本文还会给出该经典模型的框架介绍以便读者理解.问题和模型都将列在方框内.

3.1 量子梯度估计法(quantum gradient estimation)

在许多优化方法中，特别是迭代方法的梯度下降法与牛顿法，都需要目标函数的梯度信息，因此梯度估计是这类方法的核心技术之一.量子梯度估计法于2005年由麻省理工学院的Jordan提出[69].

梯度估计问题(查询模型)：

给定：函数f:Rd→R的查询黑盒Of(查询返回询问点的函数值)，点x=(x1,x2,…,xd)∈d.

该工作研究的是查询模型，在给定目标函数黑盒的情况下，量子梯度估计算法只需要调用O(1)次查询黑盒，即可近似计算出目标函数在某点的梯度，与优化变量的维度无关.当目标函数估值较困难、优化变量维度较大时，量子梯度估计法有一定的优势.美中不足的是，该算法无法通过递归求解目标函数的高阶导数，求n阶导数需要额外的2n次查询来计算所需要的相位信息，因而失去了量子优势.此工作主要使用了量子相位估计技术.2019年，来自荷兰国家数学与计算机中心与微软研究院的研究人员合作改进了量子梯度估计法[70]，并指出原有的量子梯度估计法采取的黑盒输入模型过强，实际上难以达到所需精度，因此改而研究相位黑盒输入模型与概率输入模型，并给出了这2种输入模型的转化关系.在该输入模型下，改进算法估计平滑函数的梯度时在查询复杂度上有二次(quadratic)加速，并且证明了量子优化产生的大多数目标函数会满足必要的平滑条件.

3.2 量子梯度下降法(quantum gradient descent)

迭代方法在无闭式解的优化问题中有非常广泛的应用，梯度下降法就是其中一种迭代方法.梯度下降法从初始的、未经优化的解开始，每轮根据与目标函数的梯度有关的更新规则迭代更新解.由于梯度方向是函数增长速度最快的方向，梯度的反方向是函数下降速度最快的方向，因此参照梯度信息进行迭代，能更快地获得满足要求的近似最优解.

由于量子计算的特性，运用迭代方法时一旦其中一步失败，输入就损毁了，一切就要重头再来，这使得若要达到迭代τ次的效果，往往需要远多于τ次实现迭代操作的量子演化.

梯度下降法：

猜测初始解θ0；

针对单位范数(unit norm)约束多项式优化(polynomial optimization)的量子梯度下降法于2019年由MIT的Lloyd等学者提出[71].该方法对数据维度较大的情况有优势，且把量子计算技术推进到了非二次优化甚至非凸优化问题上.

多项式优化(带单位范数约束)问题：

给定：N2p个系数Ai1…i2p∈，其中p为正整数.

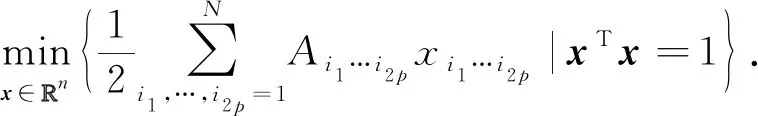
二次优化问题：

给定：A∈n×n,b∈n,c∈.

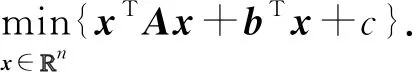
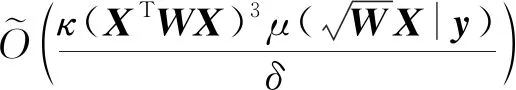
带权最小二乘问题：

给定：样例矩阵X、对应的标签向量y以及权重向量w.

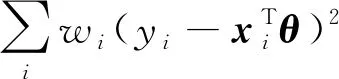
此工作运用的技术为量子奇异值估计算法(包含了量子振幅放大、量子振幅估计以及量子相位估计算法).该工作在原有QRAM的算法设计模型上作了一些改进，使得量子奇异值估计算法的时间复杂度由原来的与待分解矩阵的F范数有关，改进为与最大行范数与F范数两者之间的较小者有关.由于有不少现实问题待分解的矩阵的行范数都是有界的(boundedl1norm)，这一改进是有应用价值的，而且该改进也可以运用在量子解线性方程上.

3.3 量子在线梯度下降(quantum online gradient descent)

在线凸优化是在线学习中的一个重要的框架，是凸优化与博弈论的交叉领域，在决策问题中有非常广泛的应用，如在线路由问题、投资组合问题以及推荐系统等，都可以用在线凸优化的框架建模，并用相关技术解决.

在线凸优化模型：

给定凸集K⊆n，凸函数族F:n→.

决策者依序进行T*轮决策，在第t∈{1,2,…,T*}轮时：

1)在凸集K中做出决策xt;

2)遭受损失ft(xt)，其中ft∈F由对手选取或者由环境生成;

3.4 量子牛顿法(quantum Newton’s method)

牛顿法是一种处理无约束优化问题的迭代方法，相比每次迭代沿着梯度方向移动的梯度下降法，牛顿法把曲率也考虑在内，因此往往能加快收敛速度.梯度下降法与牛顿法之间是迭代复杂度与迭代次数之间的相互转化，每次迭代考虑更多信息的牛顿法自然单次迭代计算复杂度会更高，但由于收敛更快，因此迭代次数相应下降.2种方法不能简单说孰优孰劣，各有不同的适应场景.

牛顿法：

猜测解θ0；

3.5 连续变量量子近似优化算法(quantum app-roximate optimization algorithm for continuous variable)

针对连续优化问题的量子近似优化算法于2019年由滑铁卢大学的Killoran等学者提出[74].该工作参考了离散版本QAOA的思路，并用量子粒子势能动力学(quantum dynamics of particles in energy potentials)的技术编码目标函数.该算法适用于有约束与无约束优化，稍加修改也可以解决离散优化问题.文章作者给出了使用此算法最小化非凸Styblinski-Tang函数的数值模拟实验.

同样地，该工作相对现存经典技术的优势仍待进一步论证，且此版本的实现难度要比离散版本高，超出了目前量子计算机可实验的范围.

3.6 量子内点法(quantum interior point method)

内点法是处理有约束优化问题的迭代方法之一，常用于线性规划与二次规划，实际应用面与著名的单纯形法分庭抗礼，而且相较于非多项式算法的单纯形法，内点法是多项式算法，因此在大规模的线性规划问题中有更大的用武之地.

内点法：

松弛变量，把待优化问题的不等式约束条件转化为线性不等式约束；

目标函数中引入不等式约束条件的屏障函数(barrier function)，构造中央路径(central path)函数；

用牛顿法沿着中央路径寻找最优解.

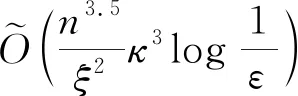
在内点法中，计算牛顿线性系统矩阵(Newton linear system matrix)是非常花时间的，而该文提出了构造牛顿线性系统矩阵块编码的量子技术，加速了这一过程，主要运用的是量子态层析技术.该文作者同时证明了算法的收敛速度与经典方法一致，因此量子内点法所需的迭代次数与经典算法一致.综合每次迭代的加速而言，量子内点法是一个理论突破.

2019年，文献[75]的2名学者与Szilágyi合作先后发表3篇文章，分别把量子内点法扩展到解决二阶锥规划[76]，以及应用到投资组合问题[77]与支持向量机[78]上.

二阶锥规划问题:给定:A(i)∈RRm×ni,ci∈RRni,i∈[r],b∈RRm.求:minx1,…,xr{∑ri=1cTixi∑ri=1A(i)xi=b,xi∈Lni},其中Lni=x=x0;x～ ∈RRni x～≤x0}为洛伦兹锥(Lorentz cones),∀i=[r]. 投资组合问题:投资者需要对m只投资产品的资金分配做T轮决策,每轮结算后根据之前的投资决策进行下一轮的分配计划,最终目的是使得总收益最大化.

3.7 量子半正定规划(quantum semi-definite pro-gramming)

半正定规划是凸优化问题的一个分支，针对的是目标函数为线性函数、优化变量约束在光谱面上(半正定矩阵构成的锥体与仿射空间的交集)的优化问题，存在多项式时间的经典算法.由于半正定规划在现实中应用面广，输入规模大，因此多项式时间仍然不能满足发展需要.2017—2019年，量子半正定规划法经过了多次迭代，并得到了快速发展.

半正定规划问题(原始形式):给定:A1,A2,…,Am,C∈RRn×n,b1,b2,…,bm∈RR.求:max{tr(CX)|∀j∈[m],tr(AjX)≤bj,X≥0}. 半正定规划问题(对偶形式):给定:A1,A2,…,Am,C∈RRn×n,b∈RRm.求:miny∈RRm{bTx|∑k∈[m]ykAk≥C}.

量子半正定规划方法于2017年由加州理工学院的Brandão与微软研究院的Svore提出[79]，该算法比经典算法有着关于矩阵维度的平方级加速，且当矩阵越稀疏，优势越明显.量子吉布斯采样(quantum Gibbs sampling)与乘权法(the multiplicative weight method)是实现该算法的关键技术.

文献[79]的作者还与马里兰大学的研究人员合作，针对设备带误差的情况进一步优化了量子半正定规划算法[80]，使得上界进一步逼近下界.与文献[79]不同的是，该算法使用的是量子态输入模型直接获得纯化的混合态，且采取的是零和游戏框架.该文核心技术是用快速放大算法(fast amplification algorithm)改进了量子OR引理，提高了算法速度.

van Apeldoorn等4名学者提出了对文献[79]的改进[81]，降低了精度对算法上界的影响，并给出了所有线性规划算法的量子查询下界(因此包括了所有的半正定规划算法)，该工作还把他们的改进版本应用在了实现给定哈密顿量平滑函数与函数广义最小值查找算法上.

2018年，van Apeldoorn等2名学者综合以上的几项工作的优点以及Gentle Quantum Search引理，提出了量子半正定规划的改进版本[82].该工作给出了更优的上下界，分别论证了在量子态输入、稀疏矩阵输入以及量子算子输入这3种不同输入模型下的算法效率，并应用到阴影层析问题、量子态区分问题以及E-最优设计上.

这4项工作的复杂度上下界详见表1.

Table 1 Main Results of Quantum Semi-Definite Programming表1 主要量子半正定规划结果

需要注意的是，精度等参数对于量子半正定规划计算复杂度的影响仍然较大，因此要在实际问题上超越经典算法依然需要进一步的研究.

3.8 量子线性规划(quantum linear programming)

线性规划是半正定规划的一个特殊形式，从实用的角度比更一般的半正定规划应用更为广泛.除了3.6节提到的可用于解线性规划问题的内点法外，还有2项针对线性规划问题的量子工作.

线性规划问题(原始形式):给定:A∈RRn×m,b∈RRn,c∈RRm.求:minx∈RRm{cTx|Ax≥b,x≥0}. 线性规划问题(对偶形式):给定:A∈RRn×m,b∈RRn,c∈RRm.求:maxy∈RRn{bTy|ATy≤c,y≥0}.

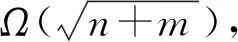
3.9 一般凸优化的量子算法(quantum algorithm for general convex optimization)

针对一般的无约束凸优化问题，马里兰大学的Childs团队[85]与荷兰国家数学与计算机中心de Wolf团队[86]于2020年分别独立地提出了相应的量子算法.

一般凸优化问题(查询模型)：

给定：凸集K⊆n的成员黑盒OK(查询返回询问点是否在集合内)，凸函数f:K→的估值黑盒Of(查询返回询问点的函数值).

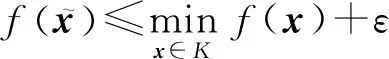
文献[85-86]的2项工作结论一致，研究的均为黑盒查询模型，思路大致类似.在给定成员黑盒(用于查询优化变量给定取值是否在可行域中)与估值黑盒(用于计算目标函数在给定点的值)情况下，2项工作的结果由表2说明.我们可以从表中看到，在时间复杂度相同的情况下，量子算法的查询上界达到了经典算法的下界，这意味着该量子算法在理论上达到了经典算法潜在的最好情况.另外，量子算法上下界仍然未紧，这意味着量子算法仍然有提升空间.由于2项工作结论一致，以下主要介绍文献[85]的技术.

Table 2 Comparison of Quantum and Classical General Convex Optimization Algorithms表2 量子与经典一般凸优化算法的对比

针对一般凸优化问题的量子算法使用的主要是量子梯度估计技术，从估值黑盒出发通过量子梯度估计求得分离超平面，经由分离超平面再得出最小化线性函数的方法，最后得出一般凸优化问题的算法，这过程中综合运用工程中常见的误差缩小技术与函数缓和技术处理边界不光滑等会影响算法性能与误差的问题.

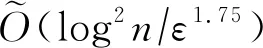
4 总 结

优化问题在生产生活中无处不在，经典计算领域把优化作为一个正式的学科分支进行研究已经有一百多年的历史，而最优化方法的起源甚至可以追溯到三四百年前费马、拉格朗日、牛顿以及高斯的微积分时代.随后经历了高度依赖一阶、高阶导数的分析算法阶段、用准确度交换速度的启发式算法阶段，以及高度依赖数据的代理模型阶段.如今在工程实践中，各类方法高度融合，产生着巨大的经济社会效益.

但纵使已经研究了数百年，在优化领域还一直有许多难题尚未得到有效的解决，有如大部分的非凸优化问题、组合优化里的NP问题，以及许多规模极大的P问题，都还处于探索阶段.而量子计算的兴起为这些难题带来了新的希望和探索方向.量子算法已经在不少问题上相对于经典算法带来了加速优势，但由于中等规模量子计算机目前依然昂贵，大型的通用量子计算机难见踪迹，因此量子优化算法的设计目前依然处于理论分析难、实验成本高的阶段，学术界与工业界都迫切盼望量子计算能在基础理论与软硬件技术上有进一步的突破.

本文通过对量子优化算法研究方面的梳理观察得出4方面：

1)从时间上看，连续变量的量子优化算法是近年的趋势，也将会是未来短期内的研究热点.这并非说组合优化不重要，而是组合优化问题有很大一部分是NP问题，要找到高效的量子算法具有挑战性.已有的针对组合优化问题的量子算法要么是采用Grover算法，在某个子过程达到根号级别加速，要么就是采用无法在理论上分析复杂度的启发式算法，而目前的量子计算机规模还不足以验证启发式量子算法的应用价值.连续变量优化问题似乎更有希望获得更多的量子加速，而且其应用面也因人工智能的发展而日益广泛.

2)量子优化使用的基本量子技术的核心思想大多都是1995—2008年提出的，HHL算法以及Jordan量子梯度估计法均为1995年相位估计算法框架的延展，幅值放大技术为1996年Grover算法的延展，而哈密顿量模拟算法以及量子随机存储技术也已有10～20年的历史.若需要寻找新的方向，还需要在最为底层的算法上有突破.

3)除启发式算法外，主要的量子优化算法相对于经典算法都在理论上体现了一定的加速，既有体现在时间复杂度的加速，也有体现在查询复杂度上的加速.一般来说，问题的计算复杂度下界往往很难证明，但查询复杂度的下界证明有如对手法[89]等较成体系的方法.纵观现有工作，在一般凸优化问题的查询模型上[85-86]寻找量子优势是很有希望的，因为其量子上界已经达到经典下界，且量子上下界还未紧，还有改进空间.

4)目前获得量子加速的优化问题十分有限，优化领域依然存在许多值得量子计算科学家探索的问题，如优化领域的难题：非凸优化.对凸优化研究的深入是经典优化领域的一个分水岭[90]，因为凸函数具有极小值即最小值等良好特性，使得凸优化问题大多都有可行、高效的算法，因此凸优化问题与能转化成凸优化问题的优化问题被认为是较易解决的.相对地，解决非凸优化则比较困难.现在的量子优化算法中，针对的线性规划、二次规划、半正定规划问题都是常见的特殊凸优化问题，都属于经典优化领域认为较易解决的部分，针对非凸优化的量子算法还很少.再者还有更多贴近实际应用的优化问题，如引入更多约束条件的约束优化、目标函数不单一的多目标规划、带有不确定性的不确定规划、问题随时间而变的动态规划、部分变量要求为整数的混合整数规划等.经典优化对于这些优化问题均有系统的研究，而量子计算目前依然缺席，均可进行探索.