量子谱回归算法
2021-09-13潘世杰万林春秦素娟温巧燕
潘世杰 高 飞 万林春 秦素娟 温巧燕
1(网络与交换技术国家重点实验室(北京邮电大学) 北京 100876) 2(密码科学技术国家重点实验室 北京 100878)
量子计算展示了其相对经典计算的强大优势[1-2].在处理特定的问题时,如大数质因数分解[3]、无结构数据搜索[4]、稀疏线性方程组求解[5]和低秩矩阵主成分分析[6],采用量子计算的方式具有比经典计算方式低得多的复杂度.近年来,一些研究人员将量子强大的计算能力用在处理经典计算机上具有较高复杂度的机器学习问题,取得了一系列成果,包括量子回归算法[7]、量子支持向量机[8]、量子生成对抗网络[9-10]、量子神经网络和量子数据挖掘[11]等.
子空间学习是机器学习的重要部分.现实世界的数据大多数是以高维的形式出现,而决定计算任务——例如分类和回归——结果的有效维度往往很低.由于直接处理高维数据不仅需要消耗大量计算资源,还会导致维数灾难(the curse of dimensionality)问题,因此子空间学习被提出,用来把数据集从高维降到低维,同时保持数据潜在的结构.人脸识别的结果表明,通过子空间学习进行降维,可以显著地提高算法的性能[12].尽管子空间学习可以部分解决高维数据的学习问题,但子空间学习本身通常也需要很高的复杂度,因此如何降低子空间学习的复杂度是一个很有实际意义的问题.一个自然而然的想法是将量子计算应用于子空间学习,以达到更低的算法复杂度.
常用的子空间学习算法包括主成分分析(principal components analysis,PCA)[13]、线性判别分析(linear discriminant analysis,LDA)[14]、局部保持投影(locality preserving projections,LPP)[12]和邻域保持嵌入(neighborhood preserving embedding,NPE)[15]等.子空间学习算法如LDA,LPP和NPE,通常需要进行稠密矩阵的特征分解,这往往需要消耗较高的计算资源.为了降低计算资源,2007年Cai等人[16]提出了谱回归降维框架,该框架包含了很多现有的子空间学习算法,如LDA,LPP和NPE.在同一篇文章中,针对结合标签信息来构造对应图的子空间学习,Cai等人提出了高效谱回归.Cai等人提出可利用权重矩阵的特殊结构,结合格拉姆-施密特正交化来得到稠密矩阵的特征向量,而不需要对稠密矩阵进行特征分解,从而把复杂度从维数的立方降低为维数的一次方.另外,因为引入了线性回归,所以谱回归中也可以很自然地加入正则化参数,使得算法可用于数据矩阵是病态矩阵的情况.
在量子领域,Lloyd等人[6]率先提出了量子主成分分析算法(quantum principal component analysis algorithm,QPCA),算法相对经典算法具有指数加速效果.需要指出的是,尽管该算法被称为QPCA算法,但实际上如果要维持量子算法的加速效果,该算法只能用来得到低秩(或者近似低秩)矩阵的较大的特征值,以及以量子态形式得到对应的特征向量;另外,如果矩阵有重特征值,那么我们无法通过量子主成分分析得到重特征值对应的一组特征向量,而只能得到特征向量的叠加态.随后,Yu等人基于量子PCA算法,提出了量子PCA降维算法,当降维后数据的维数为训练数据维数的对数时,他们的量子算法相对经典算法实现了指数级的加速[17].Cong等人实现了量子LDA算法,与经典算法相比有指数级的加速效果[18].Meng等人基于谱回归降维框架[16],首次提出了正则化子空间学习的量子谱回归算法(MYXZ算法,以作者姓名首字母命名),并在降维数据的项数m和数据的特征数n满足m=O(lbn)时,算法具有多项式加速效果[19].尽管如此,MYXZ算法仍然存在有待改进的地方.首先,MYXZ算法在算法的第一步,即求一般特征值问题时用了稀疏哈密顿量模拟,当处理的矩阵是稀疏矩阵时,算法具有良好的加速效果,但实际应用中存在很多矩阵不稀疏的例子,例如LDA,此时用稀疏哈密顿量模拟没有加速效果.其次,如果算法第一步的解中有相同的特征值,也会导致MYXZ算法无法得到相应的特征向量(只能得到特征向量的叠加态)而导致后续步骤出错.最后,MYXZ算法的加速基于假设m=O(lbn),其中m为数据的项数,n为数据的特征数.因为谱回归的原始文献[16]的重点在于把算法复杂度中的因子m3降至m,而对于m=O(lbn)的情况,谱回归本身只有很小的加速效果,因此我们认为m=O(n)是更符合实际情况的假设.
本文首先对MYXZ算法进行了细致分析,并指出了算法的局限性.然后,我们提出了一个改进算法,该算法采用了量子奇异值估计技术(quantum singular value estimation,QSVE)[20],而不是稀疏量子主成分分析来求解一般特征值问题,在处理稠密矩阵特征值问题时,QSVE具有更低的复杂度.当m=O(n)时,我们的改进算法相对经典算法有多项式加速效果;当算法的第1步涉及的矩阵是稠密矩阵时,我们的改进算法相对MYXZ算法有多项式加速效果.其次,针对结合标签信息来构造对应图的子空间学习算法,例如LDA和带标签的LPP,NPE,我们提出了相应的量子算法.我们把文献[16]中提出的高效算法中复杂度较高的岭回归部分设计成量子算法,并行得到多个岭回归结果;而复杂度较低的部分(即格拉姆施密特正交化)仍然采用原算法实现.这样做的好处在于既规避了稠密矩阵特征分解的问题,也利用了量子的加速效果.另外,为了算法的完整性,我们给出了对新输入数据进行降维的实现方式.当m=O(n)时,我们的算法相对经典的高效谱回归算法具有多项式加速效果.
1 正则化子空间学习的谱回归
在本节中,我们将对正则化子空间学习的谱回归进行回顾,并介绍其复杂度.
1.1 谱回归
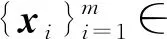
令G表示由m个顶点构成的图,每个顶点对应一张人脸图像即xi,W为一个m×m的权重矩阵,其元素表示图G中顶点i和顶点j之间的权重.谱回归是一个降维算法的框架,通过W矩阵的不同选取方式,能得到不同的降维算法,如线性判别分析、局部保持投影和邻域保持嵌入.谱回归的提出是为了避免降维算法中复杂度较高的稠密矩阵特征分解.
谱回归主要包含3个步骤:
1)求解最大特征向量问题
Wy=λDy,
(1)

2)求解c-1个最小二乘问题
(2)
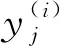
3)对新数据x进行降维,令A=(a1,a2,…,ac),则降维后的坐标为
yx=ATx.
当样本数m小于特征数n时,优化问题(2)是病态的,一种常见的做法是采用岭回归的方式,引入正则化参数α,即求解优化问题:
此时ai的解析解为
ai=(XXT+αI)-1Xy(i).
引入正则化参数的谱回归被称为正则化子空间学习的谱回归.
在文献[16]中,作者提出一种高效的谱回归求解方法.对于结合标签信息来构造对应图的降维算法,如LDA以及有监督的LPP和NPE,其最大特征向量问题(即式(1))的求解是平凡的.不妨假设数据是按标签信息排列的,则
其中W(t)是mt×mt的矩阵,mt为第t个类别的样本数,此时可以直接给出式(1)的最大特征值1对应的c个特征向量,即
另外,显然全1向量1=(1,1,…,1)T也是式(1)中最大特征值1对应的特征向量.因为对所有的W,1都是式(1)中特征值1对应的特征向量,因此1并不包含关于问题的任何信息.为了去除和1相关的冗余信息,文献[16]中提出的方法是取1为第1个正交向量,其余c-1个特征向量由y(i)通过格拉姆-施密特正交化得到.最后去掉1,就得到了我们想要的c-1个相互正交的特征向量,也即式(1)的解.
1.2 谱回归的复杂度
2 正则化子空间学习的量子谱回归
本节将对正则化子空间学习的量子谱回归进行回顾,并对算法进行分析,给出算法复杂度.
2.1 量子谱回归
2019年,Meng等人提出了正则化子空间学习的量子谱回归算法[19](MYXZ算法).该算法没有利用文献[16]中的核心思想,即对于结合标签信息来构造对应图的降维算法,其最大特征向量问题的求解(式(1))是平凡的,而是直接用量子主成分分析[6]的方式来对矩阵进行特征分解.
MYXZ算法主要包含2个步骤:
1)用稀疏矩阵量子主成分分析和量子矩阵向量乘法来求式(1)的解y(1),y(2),…,y(c-1).


2)用量子算法求
ai=(XXT+αI)-1Xy(i).
MYXZ算法假设矩阵X事先存储在一个树状的QRAM中,基于量子稠密线性方程组求解技术[16],设计出量子稠密矩阵岭回归技术,可直接用于求ai.
MYXZ算法没有考虑算法的第3步,也即针对一个新输入的数据x,输出其降维后坐标yx=Ax.
2.2 算法分析
本节将结合文献[19]中的假设,对算法及其复杂度进行分析.

3 改进的量子谱回归
在实际应用中,往往样本数量m和提取的特征个数n的规模是相差不大的,另外,在谱回归的原始论文中[16],谱回归算法的优势在于降低了复杂度中参数m的次数.如果m≪n,谱回归的加速效果并不明显.因此在改进的算法中,在其他参数假设不变的前提下,我们希望在m=O(n)时,量子算法相对经典算法有显著加速效果.
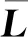
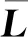


4 高效谱回归的量子算法
在文献[16]中,Cai等人针对结合标签信息来构造对应图的降维算法,如有监督的局部保持投影和邻域保持嵌入,提出了一个高效的实现方式.对于这类降维算法,式(1)的最大特征值1是c重特征值,因而MYXZ算法无法进行处理.我们提出了这类子空间学习问题的量子谱回归算法.我们的算法中也用到了MYXZ中的部分过程.
4.1 算法过程
考虑到量子主成分分析的局限性,我们直接采用经典的方式来求式(1)的解.我们的算法步骤为:
1)令第1个特征向量为全1向量(1,1,…,1)T,通过对
进行格拉姆-施密特正交化,得到c-1正交的特征向量,作为式(1)的解,记为y(1),y(2),…,y(c-1).
2)把y(1),y(2),…,y(c-1)存储到QRAM中,制备量子态
3)对第2量子寄存器,执行稠密矩阵岭回归量子算法,得
4)针对新输入的量子态|x〉,用量子低秩矩阵向量乘法,来求其降维后量子态|y〉.
我们算法的第4步即对新输入的数据进行降维,这正是子空间学习的目的.MYXZ算法没有给出算法的降维过程,为了算法的完整性,我们将给出降维过程以及其复杂度分析.
4.2 算法分析

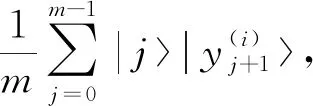
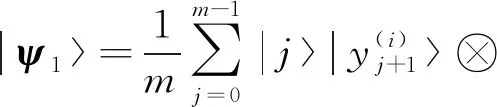
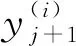

为了方便对4.1节所述的步骤4的分析,我们定义对数据的量子访问[21]:
定义1[21].如果存在以下变换可以在复杂度T内实现,那么称我们可以通过量子访问矩阵A∈n×m:

其中,i∈{1,2,…,n},Ai表示矩阵A的第i列构成的向量.


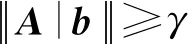
综上,算法的总复杂度为

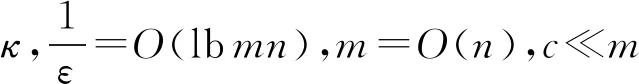
相关算法的复杂度对比和适用条件如表1所示.需要注意的是,我们没有把降维过程(即4.1节中的算法步骤4)的复杂度列在表中,因此表中量子高效谱回归的总复杂度比上面算出来的复杂度稍低,但并不影响对比结果.

Table 1 Comparison of Complexity and Applicable Conditions of Classical and Quantum Spectral Regression Algorithms表1 经典和量子谱回归算法的复杂度和适用条件对比
5 结 论