深埋隧道拱部围岩潜在塌落破坏上限有限元分析

胡昌文，韦彬，戴智颖，杨峰，赵炼恒

(1. 深圳市综合交通设计研究院有限公司，广东 深圳518003；2. 中南大学 土木工程学院，湖南 长沙410075)

隧道开挖后围岩受到扰动而应力重新分布[1]，形成局部落石[2]、剪切破坏[3]等危害隧道施工安全的破坏形式，且多以拱部岩体塌落形式发生[4−5]。隧道拱部塌落和围岩压力研究常用理论分析、数值模拟和现场监测等方法。如普罗托奇雅阔诺夫推出平衡拱理论；太沙基建立松散介质理论以确定衬砌垂直压力公式和滑动面[6]。目前，岩土极限分析成为解决隧道围岩稳定性与破坏模式问题的有力手段。如王永甫等[7]建立了圆形隧洞塌落破坏模式滑移线方程。武军等[8]以颗粒流椭球体理论改进太沙基松动压力公式。SAHOO 等[9]采用上限有限元分析多参数条件下圆形隧道围岩压力。LI等[10]运用Hoek-Brown 破坏准则及上限定理，明确了多圆弧截面深埋隧道坍塌机理。FRALDI 等[11]用变分法极限分析建立了矩形隧道塌落力学模型。HUANG 等[12]获得了孔隙水压力下隧道塌落数值解。刘俊等[13]采用强度折减法分析了浅埋隧道塌落破坏。白维仕等[14]以滑移线方式评价了黄土隧道坍塌拱及承载性能。孙雁军等[15]运用运动单元上限有限元揭示了隧道工作面滑移线网塌落形态。耿永旺[16]采用离散元分析了黄土隧道塌落拱形态特征。现有文献多倾向于研究浅埋隧道，如YANG等[17]对不同跨度影响下的浅埋隧道破坏进行了系列分析。通常隧道跨度增加时，围岩扰动范围更广，当隧道埋深较大时，拱部易形成潜在的塌落和松动范围，这种现象对于深埋土质隧道更为显著。本文应用运动单元上限有限元法，研究极限状态下不同跨度深埋隧道拱部的潜在塌落与松动范围，分析隧道稳定性系数和破坏规律，为施工技术方案和风险防范措施制定提供一定的参考和借鉴。

1 问题描述与假设条件

图1为本文建立的隧道拱部潜在塌落破坏分析模型图。假设模型满足如下条件：

1) 隧道围岩为均质各向同性材料，破坏服从摩尔-库伦屈服准则，容重为γ，内摩擦角为ϕ，剪胀角为ѱ，黏聚力为c；

2) 隧道处于未支护毛洞状态，且只考虑高度为h，宽度为B(半宽为b)的上台阶，隧道轮廓简化为椭圆形；

3) 隧道埋深足够大，荷载仅考虑围岩自重，模型依对称性取右侧一半。

如图1 所示，以b/h表示无量纲跨度参数，其中h不 变，b/h依 次 取1.00，1.25，1.50，1.75，2.00。围岩内摩擦角ϕ取35°～50°(按1°递增)。以ѱ/ϕ表示剪胀角的影响，取0.0，0.2，0.4，0.6，0.8，1.0共6组值。

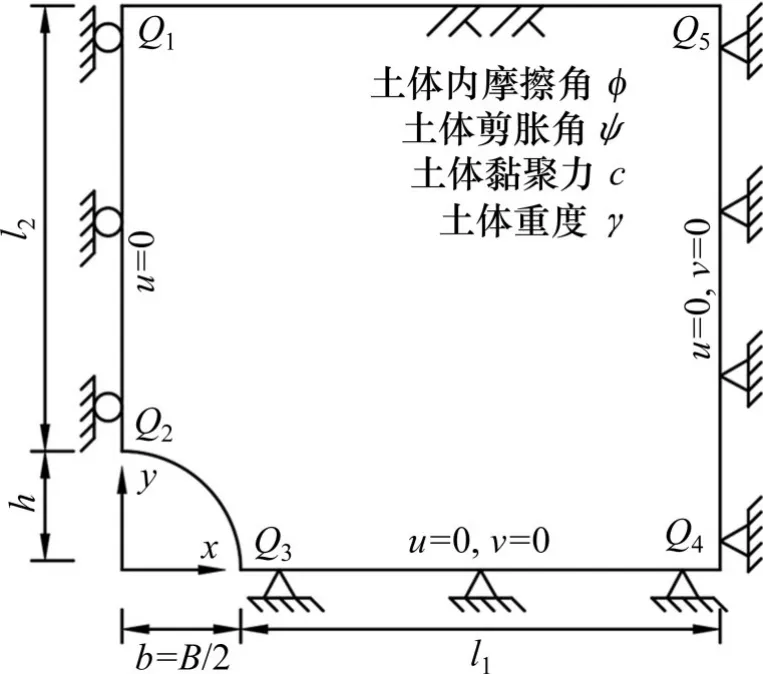
图1 隧道拱顶潜在塌落破坏分析模型Fig.1 Analysis model diagram of potential collapse failure of tunnel vault

图1中l2为隧道埋深，设置l2/h大于20。l1表示模型水平方向范围，可取l1=l2。模型左侧边界Q1Q2水平速度为0(u=0)，下部边界Q3Q4和右侧边界Q4Q5水平、竖向速度均为0(u=0，v=0)，隧道轮廓Q2Q3为自由边界。

考虑隧道拱部潜在塌落破坏由围岩自重引起，故选用无量纲量容重系数γh/c作为评价指标。于是，极限状态下对应于临界容重γcr，容重系数γcrh/c与隧道跨高比b/h，内摩擦角ϕ和剪胀参数ѱ/ϕ关联，即：

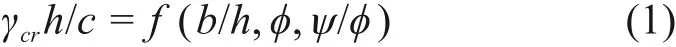
2 上限有限元模型建立

上限有限元模型划分为刚性单元，单元间设置速度间断线[18]。每个单元具有水平和竖向2 个自由度，极限状态下仅速度间断线上发生能量耗散。每个节点位置为变量，计算过程可实现间断线的优化调整，进一步通过多次网格更新形成由有效间断线网组成的近似滑移线网破坏模式。

对于隧道拱部潜在塌落破坏分析，可将围岩临界容重γcr作为目标函数，由上限定理其非线性规划目标函数表达式为：

式中：Pd,i为第i条间断线上的耗散能，nd为速度间断线的总数。

非线性规划的约束条件如式3(a)～3(h)所示：

式(3(a))为速度间断线非线性约束，而ξ′i，ξ″i为间断线上的过程变量。式(3(b))～(3(f))分别为Q1Q5和Q2Q3上的几何边界条件，式中ng1～ng5对应于各个边界上的节点数目。式(3(g))约束单元面积为正值，其中ne为单元总数；式(3(h))表示求解临界容重γcr时需施加的体力约束。Q1Q2，Q3Q4和Q4Q5上的速度边界条件见上节。

应用能量等效屈服面将最初的土体强度参数ϕ和c按剪胀角ѱ的不同转化为等效参数ϕ*和c*[19]，如式(4)和式(5)所示：

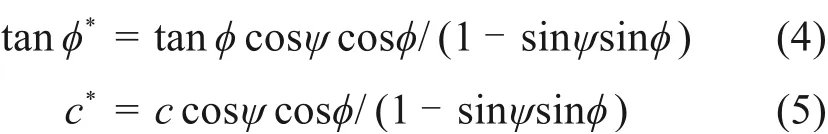
3 临界容重系数γcrh/c计算结果

3.1 计算结果对比

当隧道断面为圆形时，临界容重γcr已有相关研究，对应于本文b/h=1的情况，以下均以γcrh/c进行对比分析。取ϕ=30°，ѱ=30°，对应的数据如表1。

表1 临界容重系数γcrh/c计算结果对比Table 1 Comparison of calculation results of critical bulkdensity coefficient γcrh/c

可看出，本文γcrh/c上限解处于SAHOO 和ZHANG Jian 计算结果之间，与SAHOO, ZHANG Jian ,YANG Feng 和BANERGEE 的计算结果差距分别为26.0%，4.6%，6.0%和22.0%。比较而言，本文数值偏大，这源于隧道按上台阶半断面的情况考虑，即半圆形状对应的潜在塌落破坏，故得出γcrh/c计算数值稍大，论证运动单元上限有限元解答可靠。

3.2 临界容重系数γcrh/c规律分析

利用运动单元上限有限元对隧道塌落破坏时的临界地层容重进行分析，按上述不同b/h，ϕ和ѱ/ϕ对应获得临界容重系数γcrh/c关系曲线见图2。

图2(a)为ѱ/ϕ=0 时，γcrh/c上限解与内摩擦角ϕ以及b/h的关系曲线。由图可知，γcrh/c上限解随内摩擦角ϕ的变化较小，呈现出先增长后缓慢下降的趋势，而γcrh/c上限解随隧道跨度的增加而减小。

图2(f)为ψ/ϕ= 1时，γcrh/c上限解与内摩擦角ϕ以及b/h的关系曲线。分析可知，隧道跨度增大将显著降低破坏时的临界容重γcr，如内摩擦角45°时，b/h=2 对应的临界容重系数γcrh/c仅为b/h=1 时的39.5%，说明隧道跨度增加地层稳定性显著下降。此外，不同于图2(a)ψ/ϕ= 0 情况，ψ/ϕ= 1 时随内摩擦角ϕ增长，γcrh/c增长近似于线性增长关系。当隧道跨度大时，γcrh/c随内摩擦角ϕ增长的斜率变小。

通常，ψ/ϕ介于0～1 之间，其值越接近于1 则剪胀效应越显著。对比图2(a)～2(f)可看出，γcrh/c上限解随剪胀参数ψ/ϕ增大而增大；在这个过程中，γcrh/c上限解曲线逐渐上扬，其数值与内摩擦角的关联度变大；反之，剪胀参数ψ/ϕ较小时，γcrh/c与ϕ关系曲线转变为一略微上凸的抛物线。

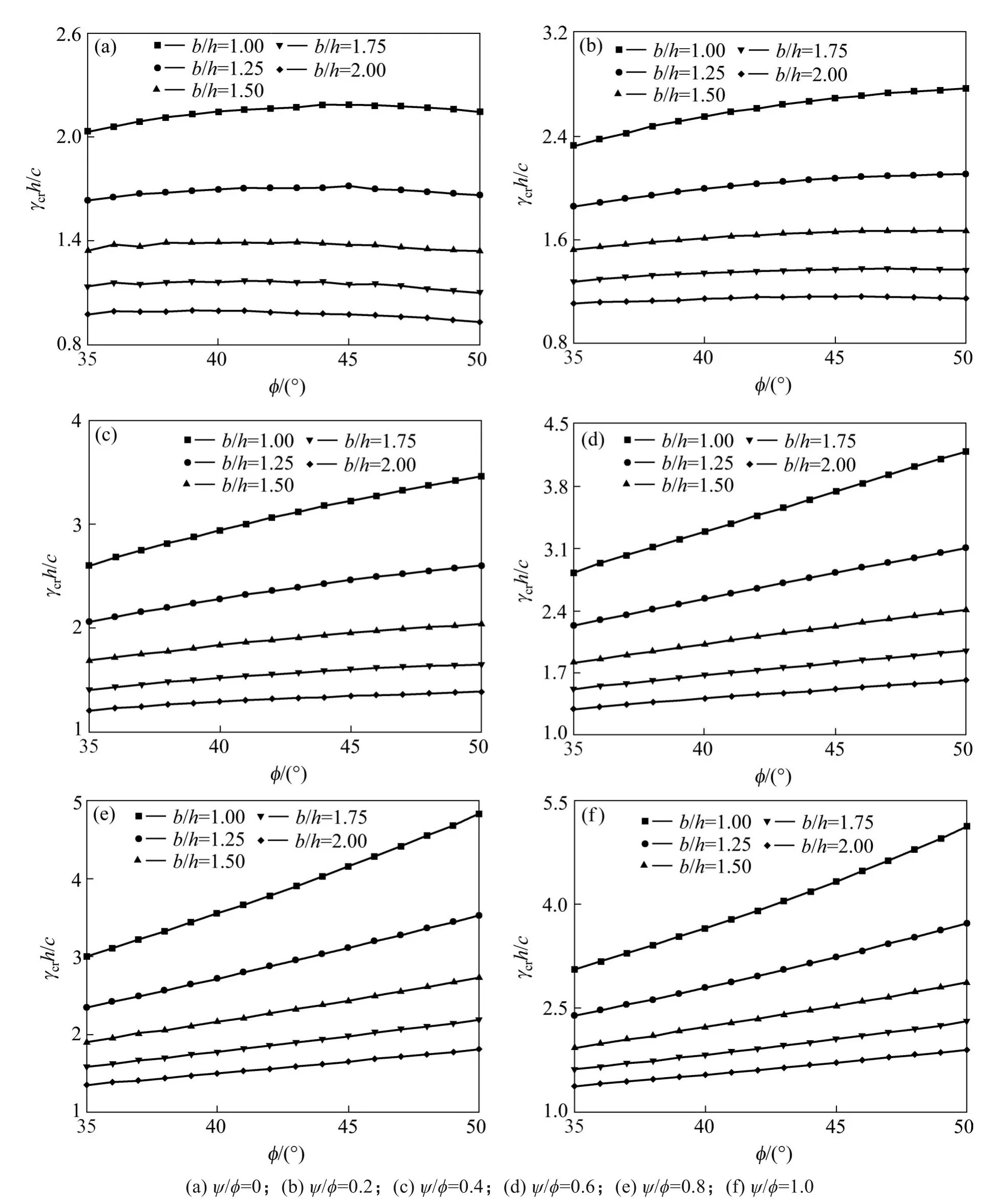
图2 临界容重系数γcrh/c与影响因素关系Fig.2 Relationship between critical bulk density coefficient γcrh/c and influencing factors

4 围岩潜在塌落破坏模式

4.1 围岩潜在塌落破坏模式对比

运动单元上限有限元程序可得到隧道拱部围岩潜在塌落破坏模式。选取ϕ=35°，ψ/ϕ= 0 和1 对应的破坏模式绘制如图3。

图3展示了速度值分布云图，该值经过归一化处理，取值范围处于0～1 之间。图3 中还叠加有效速度间断线组成的滑移线网，并以虚线表示按太沙基围岩压力理论绘制的破坏面。

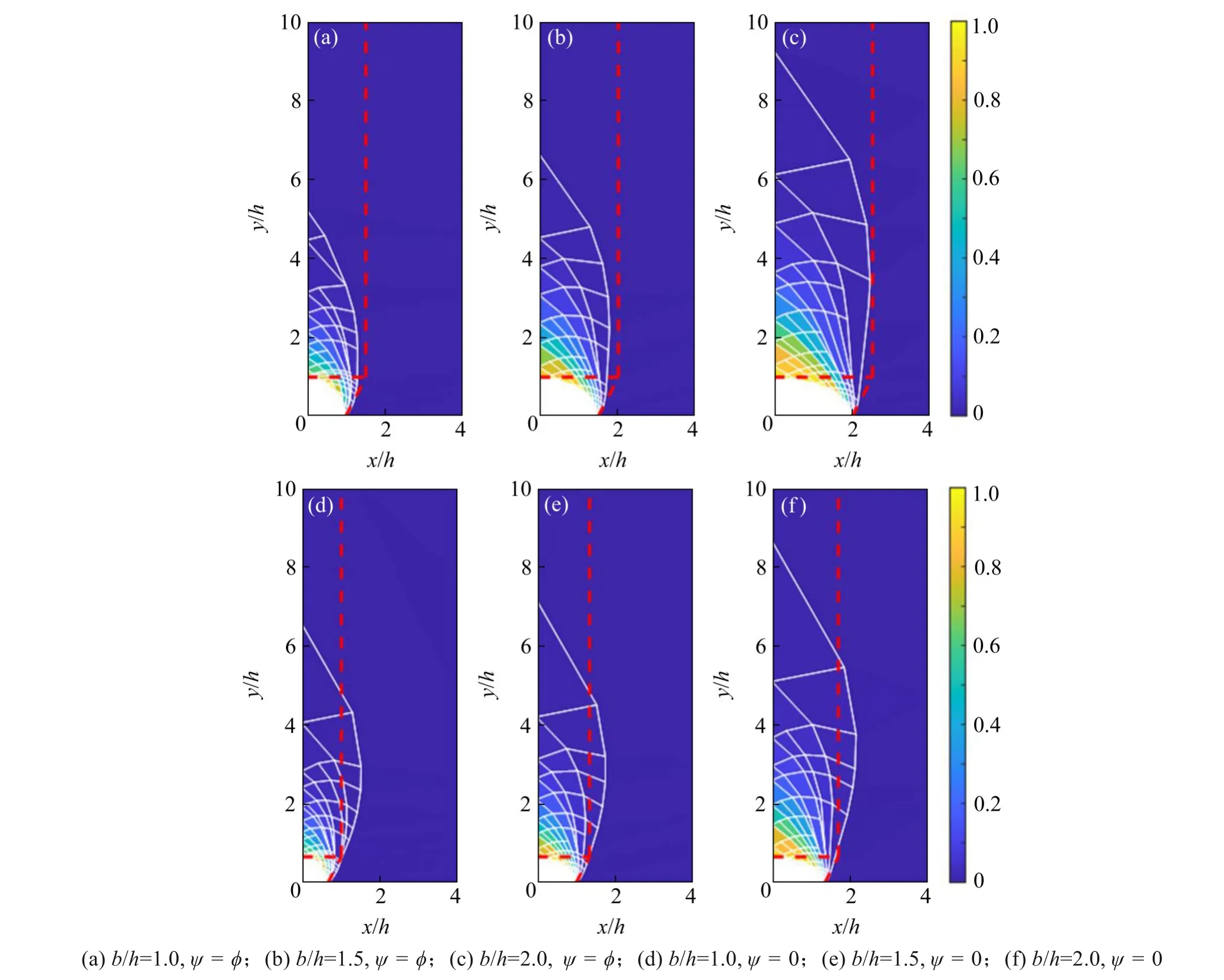
图3 围岩潜在塌落破坏模式的相对速度矢量值云图(ϕ=35°)Fig.3 Relative velocity vector nephogram of potential collapse failure of surrounding rock in tunnel arch(ϕ=35°)

由滑移线网看出，本文得到的破坏模式与太沙基理论的破坏面大致吻合。但本文破坏范围限制于一定高度范围内，这符合深埋隧道潜在塌落破坏限于局部的共识。由速度云图可知，可见耗散能占比前80%的块体单元集中于隧道拱部较小区域，该处可认为围岩潜在塌落范围，这与含平衡拱在内诸多理论相符[12,22−23]。在滑移线范围内还存在速度很小块体，此时间断线上耗散能很小，用上限原理仅能论证处于极限状态，与发生潜在塌落破坏还存在一些差异。

4.2 围岩潜在塌落破坏模式的参数影响分析

为揭示不同参数取值条件下隧道拱部围岩潜在塌落破坏几何形态的演变规律，绘制系列滑移线网破坏模式如图4所示。

1) 内摩擦角ϕ的影响

图4(a)～4(d)为圆形隧道ψ/ϕ= 0 和1，ϕ=35～50°时计算得到滑移线网破坏模式。可看出，当ϕ减小时，临界容重系数γcrh/c随之减小，隧道上方破坏范围快速增加。例如，ψ/ϕ= 1 时，当内摩擦角ϕ从40°降低到35°时，潜在塌落高度增长了59%，临界容重系数减少了19%。通常，内摩擦角降低围岩更易发生剪切破坏，引起更大范围塌落和松动趋势。

图4(e)展示了ϕ=35°～50°时，隧道拱部破坏范围外轮廓图，可看出塌落范围增长关联了内摩擦角减小，破坏模式顶端滑动面的倾角等于围岩内摩擦角。

2) 隧道跨度和高度比b/h的影响

图4(f)～4(i)列出了ψ/ϕ= 0 和1，ϕ=45°，b/h=1.25～2.0 对应滑移线网破坏模式。由图可知，当b/h增大，即隧道跨度增大时，上方潜在塌落土体范围不仅在横向上增长，在竖向范围也有较大增长，这也是临界容重系数随隧道跨度增长而快速下降的原因。

图4(j)展示了b/h=1.0～2.0 对应的隧道拱部破坏范围外轮廓图。对比图4(e)可知，潜在塌落破坏范围受内摩擦角和隧道跨度两方面的影响，内摩擦角的改变引起塌落体形状，而不同跨度隧道对应的潜在塌落范围虽有改变，但外侧轮廓差异并不大。

3) 剪胀参数ѱ/ϕ的影响

图4(g)和图4(k)～4(n)为ϕ=45°，b/h=1.5，ψ/ϕ=0～1时的滑移线网破坏模式，可以看出随着剪胀参数增大，剪胀效应使得外侧围岩受到剪胀变形土体所产生的压力，使围岩塌落破坏范围减小，上限解增大。如ψ/ϕ从0 增至1 时，塌落范围减小56%，上限解增长83%。

图4(o)展示了ϕ=45°，b/h=1.5 时不同ψ/ϕ对应的外轮廓，可知塌落范围随ψ/ϕ增大而减小趋势，随ψ/ϕ增大而放缓，如ψ/ϕ从0 到0.2，塌落面积下降32.1%，而ψ/ϕ从0.8 到1，塌 落 面 积 仅 下 降2.9%。

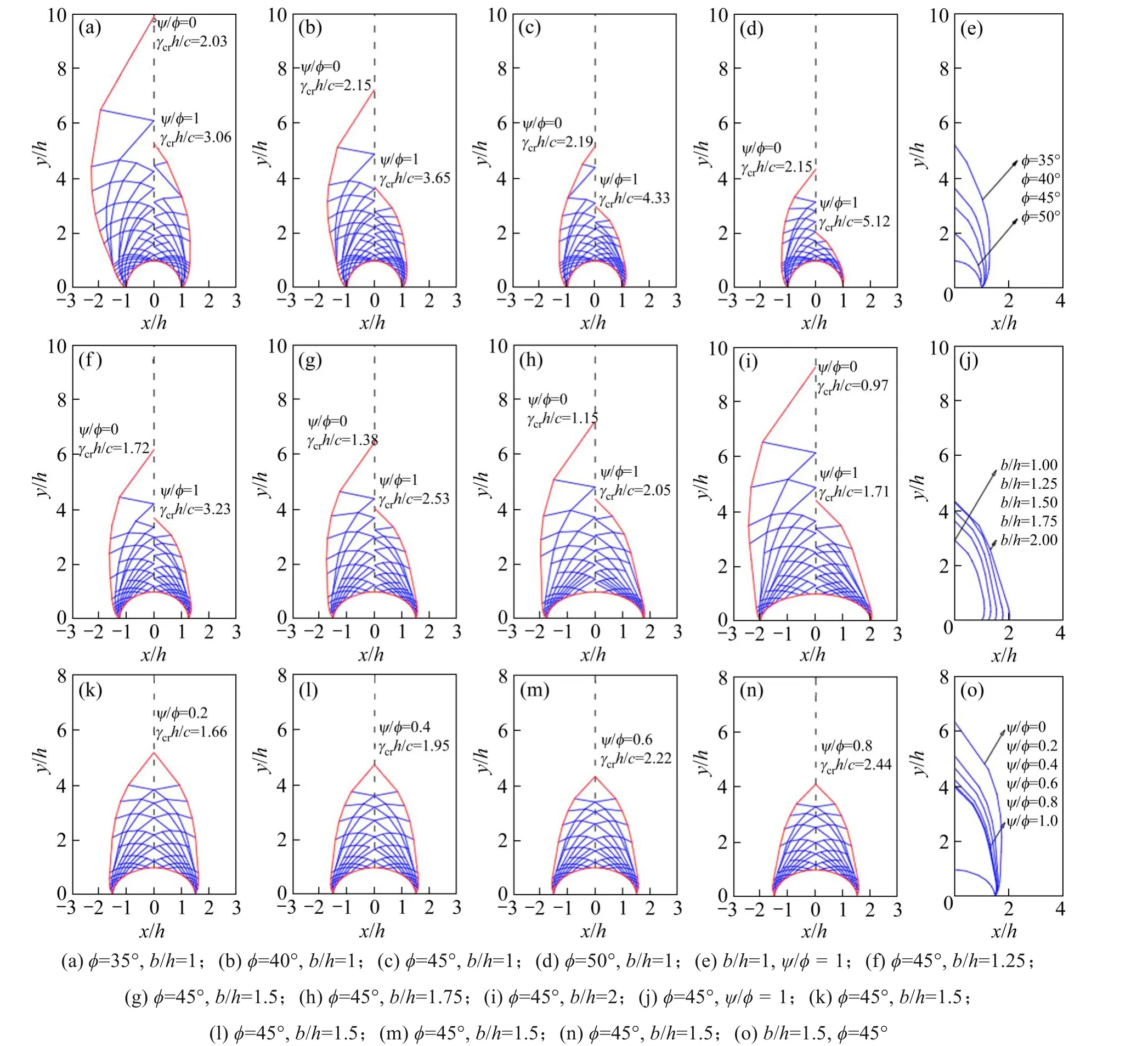
图4 隧道拱部围岩潜在破坏模式演变规律Fig.4 Evolution law of potential failure mode of surrounding rock at tunnel arch

5 结论

1)当ψ/ϕ= 1 时，临界容重系数γcrh/c随ϕ的增长而线性增长，随b/h的增长而快速降低；当ψ/ϕ=0 时，γcrh/c随ϕ增长的变化不显著，而与b/h呈反比例关系。

2)内摩擦角ϕ增长时，隧道拱顶围岩潜在塌落范围增长迅速，且塌落形状有所变化；b/h增长时塌落范围增长放缓，且塌落拱外轮廓保持不变。

3)当ϕ增长时，围岩破坏范围离拱顶稍远区域相对速度变得很小，b/h增长使得拱顶上方速度集中区域范围增长，同时γcrh/c迅速减小。