顾客感知价值和回收质量不确定下的闭环供应链定价决策
2021-09-11董景峰高贵晨杨若怡
董景峰 ,高 珊+,高贵晨,杨若怡
(1.东北林业大学 工程技术学院,黑龙江 哈尔滨 150040;2.中国科学院 深圳先进技术研究院,广东 深圳 518055)
0 引言
随着可持续发展计划的提出,在经济不断发展的前提下,社会、企业、个体的环境保护意识不断增强,越来越多的国家对能够循环使用的产品制定了相关的法律政策,并给与相关企业一定补贴;同时,消费者对社会可持续发展的关注以及环境意识的提高,也促进了相关企业对废旧产品的回收与再制造。
闭环供应链设计与管理的难度高于传统供应链,其中“经济效益”是促进企业自发进行产品生产的主要原因,随着社会环保意识的增强和国家法律政策的实施,能够进行产品回收再制造的企业不得不改变供应链设计原则,增加对废旧产品的回收与再制造。而产品的回收再制造成本低于新产品制造成本,再加上政府对废旧产品的回收再利用给予一定补贴,使制造商进行产品再制造有利可图,从而提高制造商进行回收再利用的积极性,有利于环境良好发展的可持续性。
闭环供应链存在更多不确定因素,如何在不确定因素的影响下提高整个闭环供应链的总利润是一个难点。本文在阅读国内外相关文献后,总结不确定性因素主要体现在市场需求的不确定性、废旧产品回收率的不确定性、废旧产品回收质量的不确定性。在上述不确定环境因素下,如何对再制造产品进行定价决策,使以制造商为主的闭环供应链实现整体效益最大化,是本文的研究目的。
近年来,越来越多学者对闭环供应链进行了分析和研究。在闭环供应链模型设计方面,景熠等[1]建立三级协同模型;张桂涛等[2]构建了多层闭环供应链模型;MA等[3]分析了不同的合作模型、联盟结构等。针对模型设计研究的某一方面,霍良安等[4]构建了随机需求下的闭环供应链系统;陈宇科等[5]构建了均值-CVaR度量模型;李凌雁等[6]、计国军等[7]分别基于专利保护和回收条例约束构建模型;邓乾旺等[8]给出4种不同情形下的决策模型,得出在回收质量影响下,存在最佳回收质量系数,使制造商总利润和回收率最高;HUANG等[9]构建了3种混合再制造模型,讨论了再制造能力与再制造过程中节约单位成本的作用。
在闭环供应链回收渠道的选择上,除陈军等[10]探讨的直接与间接回收渠道外,ZHAO等[11]、MAITI[12]、LIU等[13]分别探讨了回收渠道选择对决策的影响。基于回收产品的质量,周雄伟等[14]分别对不同回收渠道进行分析;谢家平等[15]探讨了销售和回收渠道比例分配问题;郑本荣等[16]实现了双渠道闭环供应链的协调;李辉等[17]、李新然等[18]、赵敬华等[19]探讨了在政府干预下的闭环供应链决策。
另外,定价是企业对其产品或服务向顾客收取费用的过程,是闭环供应链管理的关键,新产品与再制造产品定价影响着顾客的消费期望,从而决定产品的市场需求量。因此,阳成虎等[20]重构新产品与再制造产品的需求函数;于艳娜等[21]分析了需求和成本扰动对集中式和分散式信息产品供应链在定价、市场需求和最优利润方面的影响;刘广东等[22]分析了生产成本扰动下,集中供应链和分散供应链在零售价格、直销价格和销售量方面的稳健性,同时对比分析了两种类型供应链在生产成本扰动和风险规避存在差异时的定价差异性;许民利等[23]以模糊需求表征市场需求,以CVaR为风险度量工具,分析了成员风险规避的供应链在集中和分散决策条件下,风险规避系数和模糊需求参数对最优定价的影响,进而设计了收益共享契约对供应链进行协调;周维浪等[24]从消费者是否购买新产品和再制造产品出发,对闭环供应链集中决策和分散决策进行了博弈分析,并针对不同模型设计了收益共享契约和两部收费契约对供应链进行协调;林志炳[25]考虑制造商和零售商的风险意识,分析了参照价格敏感系数和风险厌恶系数等变量对定价决策和渠道效率的影响;雷倩等[26]基于Stackelberg博弈对双周期渠道供应链定价问题进行研究,分析了订货提前期、顾客对直销渠道的认可度和顾客耐心程度对制造商和零售商利润的影响;姚锋敏等[27]对零售商的行为进行了探讨;HE[28]探讨了分散和集中式决策模型下的最优决策。另外,刘盼等[29]、ZHENG等[30]、GAO等[31]从不同的方面给出了协调策略;GAN等[32]讨论了比例因子对供应链成员定价决策的影响。
闭环供应链决策复杂性主要源于上下游企业间的合作模式、顾客的感知价值和环境的不确定性等因素,上述研究分别从不同角度对闭环供应链定价问题进行了研究,其侧重于单一不确定性因素和契约协调机制,考虑顾客感知价值的文献较少,而顾客感知价值将会影响顾客对再制造品的购买意愿。顾客在购买再制造产品时会对所买产品,尤其是再制造产品进行评估,顾客的感知价值将影响顾客对再制造品的购买心理,提升再制造品的顾客感知价值有可能会对新产品形成一定竞食作用。因此,本文增加了顾客感知价值的影响,将其纳入相应模型,分析顾客感知价值对原始制造商和回收商决策变量的影响,并对其敏感性进行评估。本文以一个原始制造商和一个第三方回收商构成的闭环供应链为研究对象,基于顾客感知价值和回收质量的不确定性,分析了制造与再制造过程中制造商垄断、Stackelberg竞争博弈和Cournot双寡头竞争博弈3种情况下的定价决策、市场需求和利润分配,并给出了严格的理论证明和数值仿真。其中,本文在进行两阶段模型构建时,第二阶段中废旧产品的回收总量与第一阶段新产品的市场需求量相同,因此原始制造商对产品有主导权。
1 基本假设及变量定义
本文基于单一制造商与单一第三方回收商对闭环供应链定价决策模型进行研究,考虑市场需求、顾客感知价值和产品回收质量的不确定性,分别建立制造商、第三方回收商的利润函数,根据所得结果进行理论分析,给出闭环供应链在不确定情况下的最优决策。其中,废旧产品的回收总量等于制造商在第一阶段所生产新产品的总量。
本文的基本假设如下:
(1)假设顾客对新产品的感知价值为μ,且服从[0,1]区间上的均匀分布;由于顾客对再制造产品的感知价值相对较弱,设其为δμ,δ∈(0,1)。
(2)假设顾客对新产品的感知价值受再制造者影响,当制造商进行产品的回收与再制造时,相对于第三方回收商进行的再制造,顾客对制造商进行废旧回收产品再制造的产品有更高的认可度,其更容易接受再制造产品,从而促使再制造产品竞食制造商新产品的市场需求,表现为顾客对新产品的感知价值起抑制作用,影响因子为ω1(ω1∈(0,1));当第三方回收商对产品进行回收和再制造时,由于第三方回收商并非原始制造商,顾客对再制造产品的认可度较低,其更容易接受制造商的新产品,使再制造产品很难竞食制造商新产品的市场需求,表现为对新产品的感知价值起促进作用,影响因子为ω2(ω2∈(0,1))。
(3)假设制造商与第三方回收商都具有产品回收再制造的能力。
(4)考虑废旧产品回收质量的不确定性,由于制造商生产新产品,其对产品的了解强于第三方回收商。假设制造商进行产品回收再制造时,φ1为单位再制造产品成本降低率,φ1∈(0,1);由第三方回收商进行废旧产品回收再制造时,单位再制造产品的制造成本相对较高,φ2为单位再制造产品成本提高率,φ2∈(0,1)。
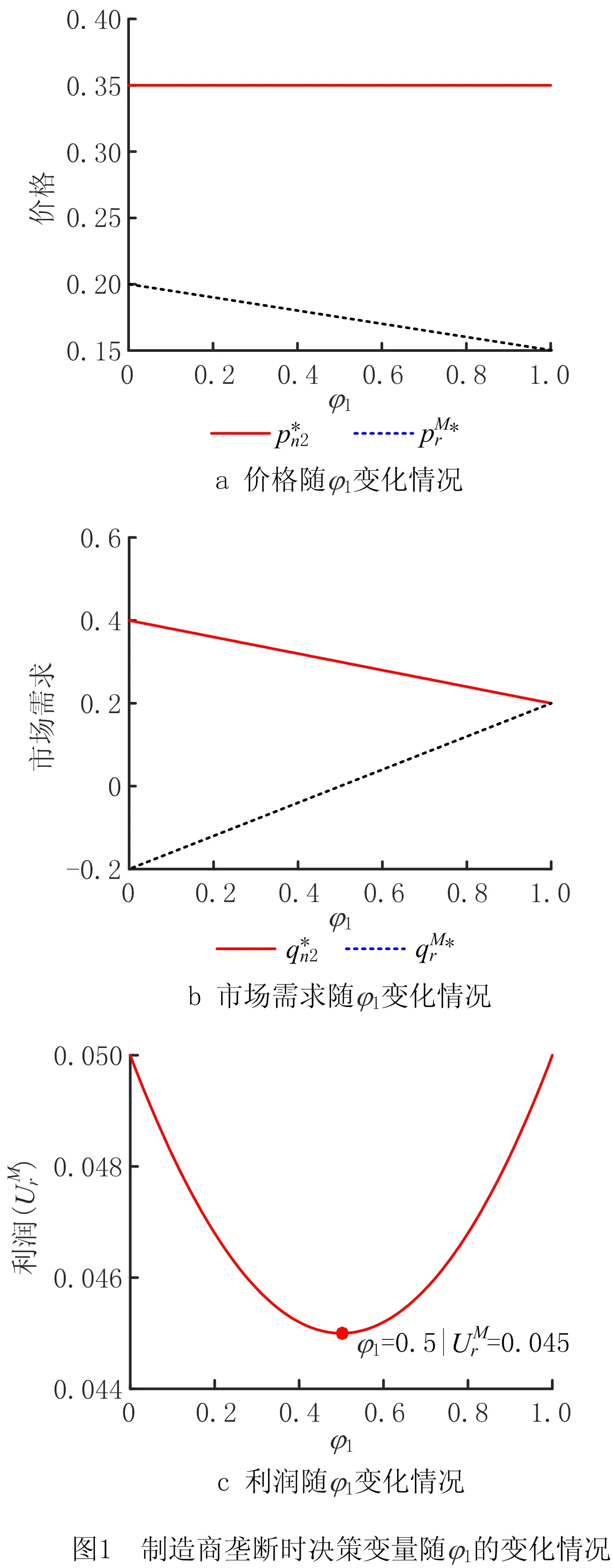
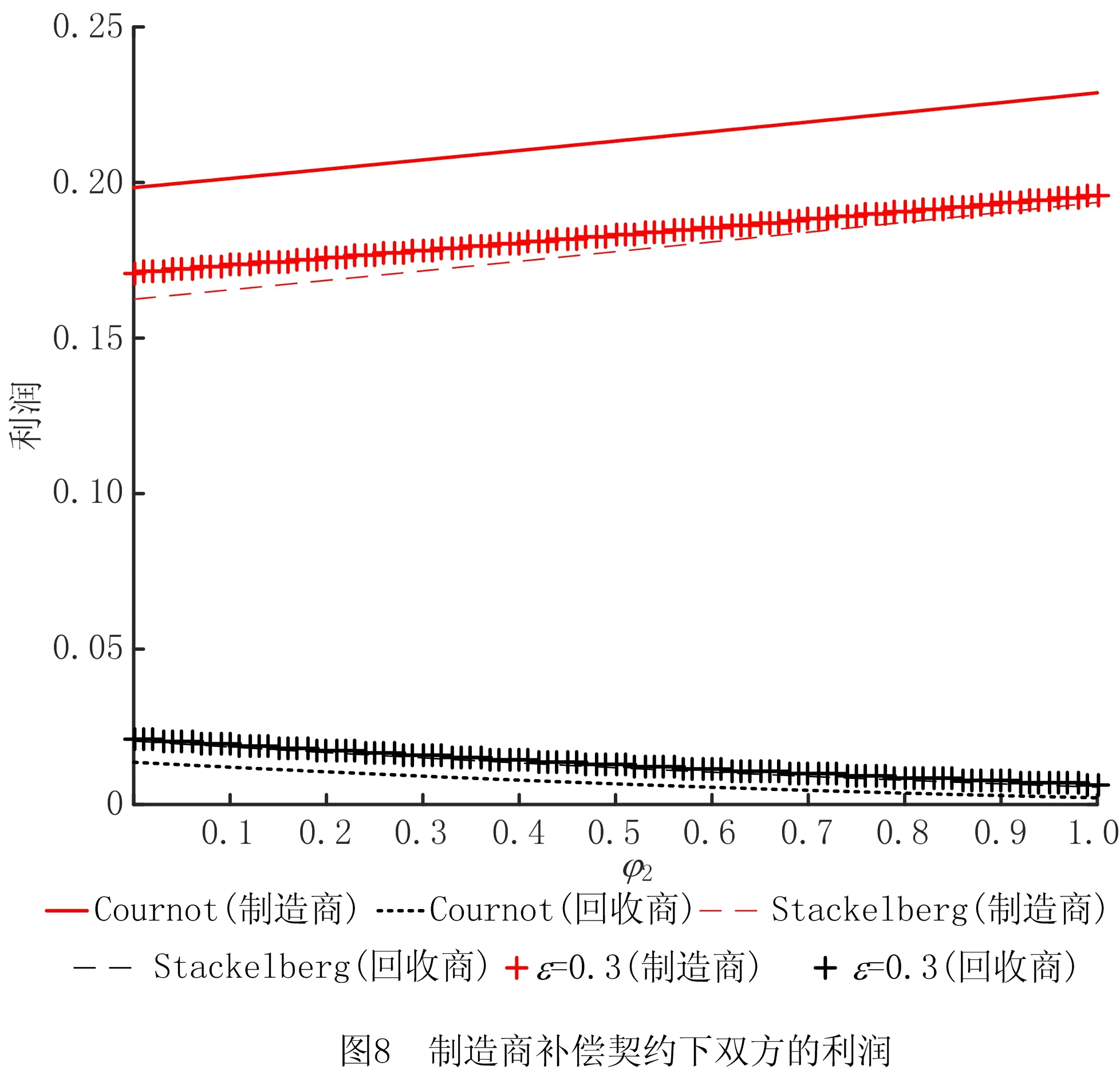
(5)假设每单位产品的生产成本、再制造成本和回收成本满足0 基本变量定义如表1所示。 表1 基本变量定义 续表1 制造商进行生产制造决策时可有多种选择,本文主要对第二阶段制造商的生产定价决策进行讨论和分析。在可回收再制造产品中,制造商对废旧回收产品具有完全控制权。当制造商选择独自进行产品生产与回收再制造时,市场上就无回收商,形成制造商独自进行产品生产与再制造的垄断局势;当制造商将产品回收再制造的权利转让给第三方回收商时,制造商与第三方回收商成为竞争关系,形成Cournot博弈局面;当制造商将回收产品销售给第三方回收商时,第三方回收商进行产品定价决策时必须考虑制造商的定价,形成制造商与第三方回收商的Stackelberg博弈局面。基于上述分析,本章进行模型构建、求解与分析。 一般而言,市场需求量与产品定价呈负相关,产品定价越高,产品的市场需求量越低。顾客消费产品时对产品本身存在一个期望价值,当顾客对产品的期望价值与产品定价的差值较大时,会表现出较强的购买欲望,否则购买欲望就会变弱。因此,本节就提高厂商的生产利润进行产品定价讨论。基于上述假设,对产品定价与产品市场需求量之间关系的分析如下: (1)第一阶段:只有制造商生产新产品 (2)第二阶段:存在新产品生产和回收产品再制造 对①情况进行分类讨论: 对①情况进行分类讨论: 在产品生产的第一阶段,只有制造商生产和销售新产品,制造商的利润函数表示为单位新产品的利润和销售量的乘积,即 命题1新产品的最优定价、市场需求量和最大利润分别为: 相对市场需求不确定下的模型构建,本节模型考虑回收质量的不确定性,将制造商与第三方回收商进行废旧产品回收时的质量不确定性表现在再制造产品制造成本的差异上,增添影响因子φ1,φ2。其中,产品的定价、市场需求量和利润值与ω1,ω2的关系与只考虑市场需求量时的情况一样,在这里仅讨论φ1,φ2与产品的定价、市场需求量和利润值的关系。 2.3.1 制造商垄断 制造商独自进行产品回收与再制造的目标函数: (1) 模型的求解与分析如下: 命题2新产品与再制造产品的最优定价、市场需求量和最大利润为: A:如果老想着要把文化带出去,让别人接受自己的文化,反而说明自己没有自信。中国文化就是世界的,我们坚持自己就足够了。每个国家都有自己独特的文化,大家互相包容,互相共融就可以了。 解得奇数阶主子式、偶数阶主子式分别为: (2) (3) 2.3.2 非制造商垄断 (1)制造商与第三方回收商形成Cournot双寡头竞争博弈模型 1)目标函数 制造商利润函数 (4) 第三方回收商利润函数 (5) 2)模型求解与分析 命题5新产品与再制造产品的最优定价、市场需求量和最大利润为: 证毕。 (2)制造商与第三方回收商形成Stackelberg竞争博弈模型 1)目标函数 制造商利润函数 (6) 第三方回收商利润函数 (7) 2)模型求解与分析 命题7新产品与再制造产品的最优定价、市场需求量和最大利润为: 证毕。 命题9当1+φ2>[2δ(1-δ)(1+ω2)-δ(2-δ)cn-(4-3δ)d]/[(4-3δ)cr]时,第三方回收商将不再进行再制造产品的生产。 2.3.3 需求和回收质量不确定下各变量变化的情况 本文基于市场需求、产品回收质量和顾客感知价值的不确定性,建立了制造商垄断和非制造商垄断(Cournot博弈和Stackelberg博弈)情况下的利润模型,并根据凹函数存在最大值的性质以及KKT(Karush-Kuhn-Tucker)条件对模型进行了求解。在模型求解与分析过程中,本文给出严格的理论证明,得到3种不确定情况下的最优产品定价、市场需求和目标函数值,并基于所得结果给出产品定价、市场需求、目标函数随影响因子变化的理论分析与证明,具体结果如表2所示。 表2 需求和回收质量不确定情况下各变量随影响因子变化的情况 从表2可以看出: (1)制造商垄断和Stackelberg博弈下,会出现制造商新产品生产停滞或回收产品再制造停滞的可能,这主要取决于制造商新产品生产的成本、顾客的感知价值和回收成本,这在命题4和命题9中进行了相应证明。 (2)对于制造商垄断的情况,很显然随着新产品成本的降低,其市场需求和利润都会随之增长,但同时也会抑制再制造产品的市场需求,这主要由于新产品对再制造品的竞食使再制造品的市场竞争力下降,再制造品所能带来的利润有限。此时,若希望制造商积极从事回收再制造,从而提升资源的循环利用,需要对制造商进行额外的激励措施。 (3)对于非制造商垄断的情况,无论制造商和回收商采用何种合作模式,再制造成本的增加都会促使再制造品的定价增加,市场减少,从而减少回收商的利润。同时,在没有再制造产品竞食新产品市场需求的情况下,新产品市场需求将增加,制造商靠生产新产品就可以增加利润,这样将抑制制造商进行回收再制造的积极性。此时,若希望制造商或回收商积极从事回收再制造,则需要制造商和回收商之间建立有效的协调机制。 以上分别研究了制造商垄断与非制造商垄断下,制造商与第三方回收商在定价、市场需求和利润方面的最优解,并对最优解进行了理论分析。本节通过算例仿真对这些命题和推论进行仿真,并进行进一步分析。假设某家电产品的有关参数为:Cn=0.2,Cr=0.1,δ=0.5,ω1=ω2=0.5,d=0.05。将数值带入制造商与第三方回收商的决策目标函数,可以得到以下规律: 图2所示为制造商垄断时,制造商决策变量随φ1和ω1变化的情况。可见,制造商再制造成本的降低对制造商利润的影响相对平缓。当再制造成本保持不变时,再制造产品的市场需求增加抑制了新产品的市场需求,使制造商利润降低,抑制了制造商进行再制造产品回收制造的积极性,此时政府政策对产品回收再利用的奖惩措施将有效保证制造商利润,从而有效驱动制造商参与产品的回收再利用。 在非制造商垄断下,当制造商与第三方回收商形成Cournot双寡头竞争博弈时,各决策变量随φ1变化的情况如图3所示,该图也验证了命题6的结论。新产品与再制造产品均存在市场需求,新产品的市场需求量随单位再制造成本提高率φ2的增大而增大,再制造产品的市场需求随φ2的增大而减小,即随着回收质量的降低,第三方回收商再制造成本增加,从而使市场需求逐渐降低。此时,第三方回收商为了获取更多利润,将会提高再制造产品的价格;而且相较于制造商进行再制造,顾客对第三方回 收商再制造产品的认可度较低。较高的再制造产品价格和更低的顾客认可度使顾客更加倾向于购买制造商生产的新产品,进一步抑制了第三方回收商再制造产品的市场需求,使第三方回收商的利润逐渐降低,制造商的利润则随新产品市场需求的提高有所提升。对于第三方回收商,通过提高再制造产品价格显然很难提升利润,其可以通过一定的营销活动积极引导顾客对原有品牌的认可度,维持并培养原品牌顾客的忠诚度,提升顾客对再制造产品的感知价值,进而提升再制造产品的市场需求并提高其利润。 图4所示为Cournot双寡头竞争博弈时,原始制造商和第三方回收商决策变量随ω2变化的情况。 显然,该策略有利于原始制造商,由于没有回收处理的负担,其利润始终处于增长的状态。尤其是第三方回收商并非原始制造商,顾客对再制造产品的认可度较低,表现为对新产品的感知价值具有促进作用,使得随着ω2的增加,原始制造商的利润呈现较大幅度的增长,因为在Cournot双寡头竞争博弈下,原始制造商和第三方回收商双方均以个人利益最大化为主要目标,第三方回收商作为独立运营主体也会极力促进利润的增长,所以由图4可见,随着ω2的增加,第三方回收商的利润和市场需求仍随之增长,其为第三方回收商的发展策略提供了参考。 制造商与第三方回收商在Stackelberg竞争下,各方决策变量随φ2变化的情况如图5所示,也验证了命题8的结论。可见,在Stackelberg竞争下,新产品与再制造产品均存在市场需求,新产品的市场需求量随φ2的增大而增大,再制造产品的市场需求量随φ2的增大而减小,而且当φ2≥0.9时,第三方回收商将不再进行再制造产品的生产。制造商与第三方回收商的利润变化与Cournot双寡头竞争博弈相似,但对于第三方回收商,在相同的φ2下会得到更多的利润。 图6所示为Stackelberg竞争博弈时,第三方回收商和制造商决策变量随φ2和ω2变化的情况。可见,新产品与再制造产品的定价随ω2的增大而增大,双方的市场需求也随ω2增大而增大,而再制造产品的市场需求增加得更快。随着ω2的增加,第三方回收商的利润和市场需求随之增长,这与φ2引起的变化不同,因此在φ2和ω2的交替影响下,第三方回收商利润和市场需求变化较缓。而ω2却会引起制造商决策变量有较大的变化,随着顾客对新产品认可度的增加,制造商利润会有较大幅度的增长。 不同竞争模式下,制造商和第三方回收商的利润随φ2(φ1)变化的情况如图7所示。制造商更愿意在Cournot博弈下生产新产品,其可以专注于新产品生产而无需进行回收,从而获得更高的利润;第三方回收商更愿意在Stackelberg博弈下进行产品回收再制造。因此,制造商和第三方回收商之间存在博弈,在市场驱动下,很难达到均衡状态。 为了达到均衡状态,可以考虑制造商补偿契约。当双方采用Cournot双寡头竞争博弈时,由原始制造商对第三方回收商极限回收补偿。制造商回收补偿契约的方式为:第三方回收商回收产品并进行再制造,当再制造产品的销量为Q时,原始制造商以价格εP对第三方回收商进行补偿,其中P为再制造产品的销售价格,ε为补偿因子。由此,式(4)和式(5)可写为如下形式: 制造商利润函数 (8) 第三方回收商利润函数 (9) 按2.3.2节中的方法对其进行求解,此时双方利润如图8所示。 由图8可见,当补偿因子ε=0.3时,在Cournot双寡头博弈下,第三方回收商利润将高于其在Stackelberg竞争博弈下的利润;同时,原始制造商此时的利润仍高于Stackelberg竞争博弈下的利润,这可以成为一组均衡解,即双方都会选择Cournot双寡头博弈进行产品的回收和再制造。当然,采用该契约需要的前提是原始制造商有意愿进行让利,以补偿第三方回收商利润的不足,而在实践中这种前提是可以出现的,例如当政府根据产品回收率对原始制造商实行奖惩机制时。 本文从闭环供应链的经济效益出发,考虑单一原始制造商与单一第三方回收商在经济利益的驱使下,在市场需求和回收质量不确定的情况下,针对制造商垄断、Cournot双寡头竞争博弈和Stackelberg博弈3种模式进行闭环供应链决策,使闭环供应链和以原始制造商为主的利润最优。本文研究未考虑政府的干预措施,旨在分析无政府干预时原始制造商与第三方回收商之间的利益博弈并进行效益分析。为了分析该问题,本文构建了市场需求及产品回收质量不确定下的3种利润模型,并根据凹函数存在最大值的性质及KKT条件对模型进行求解。在模型求解与分析过程中,给出了严格的理论证明,得到3种模式下的最优产品定价、市场需求和目标函数值,并基于所得结果给出产品定价、市场需求、目标函数随再制造成本降低率(提高率)和顾客感知价值变化的理论分析与证明。其中,本文在构建两阶段模型时,第二阶段中废旧产品的回收总量与第一阶段新产品的市场需求量相同,因此原始制造商对产品具有主导权。总体研究结果如下: (1)进行产品回收再制造将有助于提高原始供应商的利益。 (2)无论原始制造商与第三方回收商采用哪种竞争模式,回收质量的改善,即回收成本的降低,都将促进再制造品的市场需求,有利于改善第三方回收商的利益,但同时也会抑制制造商的市场需求和利润。 (3)新产品感知价值的提升将有助于改善制造商的市场需求和利润,反之也会抑制第三方回收商的市场需求和利润。 (4)从数值分析结果来看,必要的政府政策支持和引导,将有助于促进制造商和第三方回收商从事回收再制造的积极性,同时原始制造商补偿契约将有助于双方得到均衡解,能更好地实现双赢。 在后续的工作中,探讨多种不确定性因素的影响,并对闭环供应链的定价和协同机制进行研究将是十分有意义的工作。

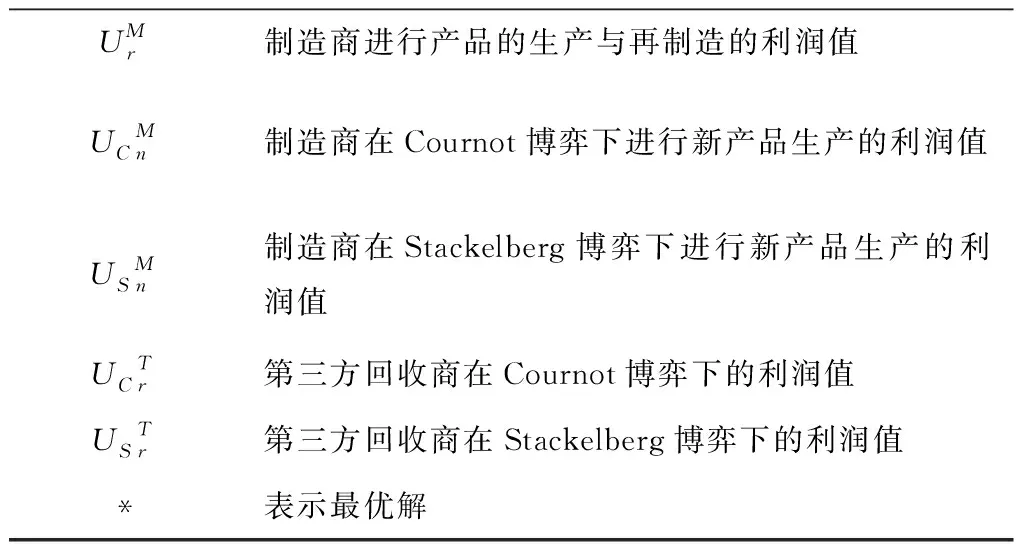
2 制造商与第三方回收商定价模型构建与分析
2.1 产品定价与需求量




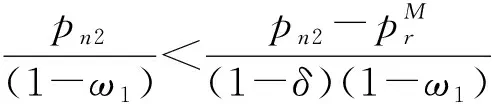





2.2 第一阶段定价模型


2.3 第二阶段需求及回收质量不确定下的定价模型
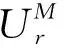









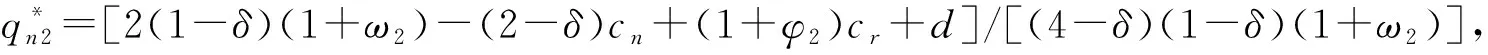
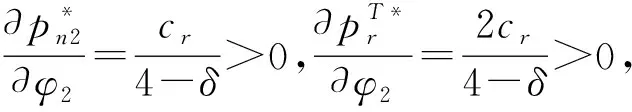


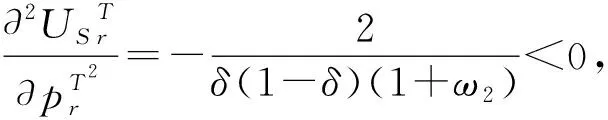




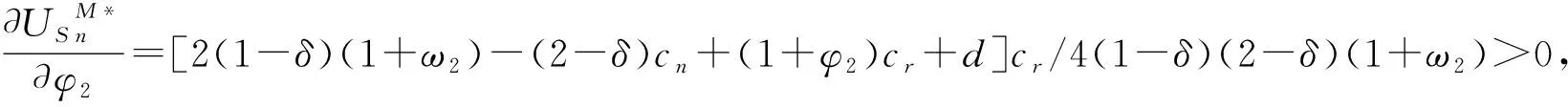


3 数值算例与分析
3.1 不同定价模型数值分析

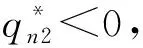







3.2 制造商补偿契约协调

4 结束语
