百叶轮抛光航空发动机叶片残余应力建模

鲜 超，史耀耀，蔺小军，刘 德

(西北工业大学 航空发动机高性能制造实验室，陕西 西安 710072)

0 引言

磨削过程中形成的残余应力对零件的抗疲劳和耐磨性能有重要影响，一般认为加工表面的残余应力是机械应力和热应力共同作用的结果，残余应力有拉应力和压应力两种状态。表面残余压应力可以延缓疲劳裂纹的产生和扩展，提高疲劳强度。因为残余拉应力容易引起零件表面沿晶损伤，从而产生表面裂纹，降低零件的疲劳强度，所以零件的加工表面和次表面更希望产生残余压应力，而不是残余拉应力。迄今为止，许多学者提出了许多研究残余应力的方法，主要有实验法、数学物理建模法和有限元模拟法3种。

残余应力的研究始于切削加工，20世纪80年代以后，学者们开始研究磨削残余应力。MITTAL等[1]在不同工艺条件下，用铝轮磨削淬火轴承钢EN31，结果表明在100 μm的磨削深度下，经过细磨后，粗磨产生的残余拉应力完全消除，而且产生了残余压应力；NEAILEY[2]研究了磨削液对磨削DIN 100Cr6钢时残余应力的影响，结果表明，纯油磨削液产生的残余应力分布优于水基磨削液，能更好地提高工件的疲劳寿命；GRUM[3]指出，考虑到工件材料的物理力学性能，选择合适的砂轮和磨削工艺参数可以获得良好的残余应力分布；FREDJ等[4]研究了磨料对AISI304工件表面残余应力的影响；YAO等[5]用树脂结合剂白铝砂轮和立方氮化硼砂轮研究了100合金钢研磨后的残余应力和影响层，分别测量了磨削力、磨削温度和残余应力的影响层，对比了两种砂轮磨削工件后的表面残余应力分布以及热—机械耦合影响层；ZOEI等[6]研究了切削速度、进给量、切削深度等磨削参数对涂层耐磨性和残余应力的影响，结果表明磨削后WC-10CO-4Cr涂层的耐磨性和残余压应力均有所提高，而且随着切削深度和进给速度的增加，切削速度的降低，残余压应力越高，涂层的耐磨性越好；CAPELLO等[7]通过实验研究了外圆磨削工艺参数和残余应力的关系，着重研究了磨削深度和工件周向速度对残余应力的影响，其中周向速度对残余应力的影响取决于磨削条件，工件进给速度对残余应力的影响不大，加工过程中产生的残余应力水平主要受扩散角、砂轮磨损和砂轮修整的影响；BERG等[8]研究了两种不同粒径金刚石砂轮对磨削后氧化镁部分稳定氧化锆(Magnesia partially-stabilized Zirconia)性能的影响，指出粗金刚石颗粒产生的残余应力大于细金刚石颗粒，所生成的氧化锆相变层更厚。

TONSHOFF等[9]用数学方法描述了磨削过程中工件表面早期生成的物理过程，通过磨削热计算工件表面的温度分布，预测工件表面的残余应力；BARBER[10]给出在弹性半平面上匀速运动的线热源引起的表面位移和残余应力的解，该解通过对瞬时点源的先前结果进行积分得到，最后的结果用贝塞尔函数表示，并给出了数值的有效级数和渐近表达式。

CHEN等[11]研究了磨削后残余应力产生的原因，探讨了残余压应力与拉应力之间是否存在过渡温度，指出磨削过程中产生的热应力是产生拉伸残余应力的主要原因，并介绍了一种描述拉伸残余应力初始温度的方法，给出了不同钢的临界转变温度；XIAO等[12]提出基于工件温度分布的分析模型，用于预测不同磨削周期下的残余应力；FERGANI等[13]提出一个以初始温度为因素的预测残余应力物理模型，该预测模型基于移动热源法，采用Timoshenko的热应力理论分析和计算热应力，并通过对这些应力施加弹塑性松弛条件求得残余应力；WU等[14]认为应力的变化会导致残余应力，并采用Boussinesq积分方法计算残余应力；SHAO等[15]提出考虑润滑和冷却的微量润滑磨削残余应力物理模型，根据磨削力和工件温度分布计算微量润滑磨削的载荷应力，然后将加载应力耦合到滚动/滑动接触算法中求解残余应力；SALONIRIS[16]提出一种不同工艺参数下残余应力分布的建模和预测方法；TONISSEN等[17]研究了快速点模式下磨削参数对残余应力的影响，指出磨削能量与残余应力有关；KARABELCHTCHIKOVA等[18]提出一个二阶系统模型，主要用于预测D2工具钢在不同热处理工艺和磨削动力学条件下的残余应力分布，其中模型假设的有效性是独立评估和验证的。

MAHDI等[19]通过耦合机械变形、热变形和相变来模拟表面磨削残余应力；NÉLIAS等[20]建立了Arthur Moore的力学模型，首次对磨具与工件接触产生的残余应力和残余应变进行了数值模拟，给出了不同静态下的结果；SALLEM等[21]建立了考虑材料性能随温度变化的外圆磨削加工有限元仿真模型，并利用SysWeld 2010软件进行了二维数值模拟；CHEN等[22]考虑金刚石刀具与工件表面摩擦产生的热机械耦合效应，研究了难加工材料超高速磨削时产生的残余应力，提出一种考虑刀具旋转运动的三维有限元方法，并分析了不同磨削条件(磨削速度和磨削深度)对残余应力场的影响；SHAH等[23]采用商用有限元软件ABAQUS，以ALSI-52100轴承钢为参考材料，开发了各种用户子程序，分析了材料的热冶金和机械性能，结果表明最佳的磨削条件组合能在工件表面产生所需的残余压应力，相变对残余应力预测结果准确性的影响非常明显；HAMDI等[24]建立了磨削过程表面残余应力的有限元力热模型，该模型以工件内的导热能为响应，以砂轮转速、工件转速和切削深度为影响因素，适用于磨削深度小于120 μm的常规磨削，结果表明在这种磨削条件下可以模拟出拉伸残余应力。考虑到百叶轮具有一定的柔性，可以避免叶片欠抛和过抛，淮文博等[25-27]、ZHAO等[28]提出用百叶轮抛光航空发动机叶片的方法。

本文综合考虑机械效应、热效应和力热耦合效应，建立了残余应力的数学模型。文献[9-13]给出了只考虑热效应条件下的残余应力的计算方法，WU等[14]采用Boussinesq积分等式预测了机械效应导致的表层残余应力，SHAO等[15]给出了综合考虑机械效应和热效应的残余应力计算方法，然而这些计算方法大多非常复杂，而且未考虑力热耦合效应。经验回归方法[16-17]虽然建立了残余应力和磨削参数的经验关系式，但是未能反映各个效应对残余应力的贡献。与以前学者提出的模型相比，本文建立的数学模型综合考虑了机械效应、热效应和力热耦合效应，并将这3种效应归结为接触弧长响应，最终得到的残余应力模型仅与接触弧长、进给速度和百叶轮线速度3个因素有关，与以前的学者提出的模型相比，该模型简单有效，且预测准确性较高。

1 试验方案及试验设备

1.1 试验设备和材料

本试验所使用的设备为西北工业大学自行研发的五轴联动数控抛光机床，因为整体叶盘叶片为自由曲面，所以设计机床的五轴联动运动形式，五轴包括X，Y，Z3个直线运动轴和A，C两个旋转轴。

考虑到整体叶盘通道狭窄，为了避免在大曲率区域附近出现欠抛光或过抛光，磨具直径值应小于其他场合，且具有一定柔性，百叶轮柔性抛光原理参考文献[29-30]。因此，磨具选择直径为13.5 mm、宽度为12 mm的百叶轮，百叶轮由砂布层叠和树脂胶粘而成，其磨粒为棕刚玉，主要成分为氧化铝。GH4169具有强度高、热稳定性好、耐腐蚀性强、高温热疲劳性能优异等综合性能，能在高温下长期有效地工作，在航空航天工业中应用广泛。因此，本实验的工件材料为镍基高温合金GH4169，在抛光前用球头铣刀对叶片表面进行了铣削加工。

1.2 符号及单位

本文涉及的符号如表1所示。

表1 符号及单位表

续表1

1.3 试验原理及试验参数

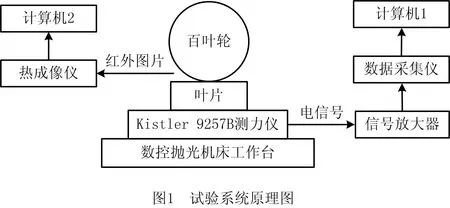
图1所示为试验测量抛光力和抛光温度的原理图。在抛光过程中，百叶轮和叶片接触后产生抛光力，测力仪将力信号转化为电压信号，经过放大和A/D转换后传入计算机，计算机便可以采集到抛光力信号。抛光温度由德国Infratec/vh-480红外热成像检测系统获取，红外图像可直接输入计算机。

实际工件抛光表面的质量形成机制非常复杂，本试验中的主轴转速、压缩量、进给速度和百叶轮粒度容易控制，本文主要考虑其对抛光效果的影响，其余影响因子不易控制，因此保持为常量。为了兼顾抛光效率和抛光表面质量，试验所采取的4个因素水平如表2所示。

表2 试验因素及水平分布

试验中，每组工艺参数在同一表面位置区域沿同一进给方向进行一次抛光，更换工艺参数时，先更换抛光表面位置区域再进行抛光。磨具在同一工艺参数条件下只抛光一次叶片，更换工艺参数后也更换磨具，同时抛光过程中的材料去除量为几十微米，磨具磨损量非常小，因此忽略磨具磨粒磨损对抛光力、抛光温度和残余应力的影响。

考虑到中心复合试验能以最小的试验次数获得最大的试验变量和试验误差信息，中心复合试验设计方法的工艺参数安排如表3所示。表中也给出了相关的测量结果，其中：抛光力数值通过三向测力仪测得，再经过坐标变换后得到，详见第3章；温度值通过红外热成像检测系统测得后经过修正得到，详见第5章；残余应力值采用PROTO LXRD残余应力测试与分析系统测得，详见第6章。

表3 工艺参数以及相关试验结果

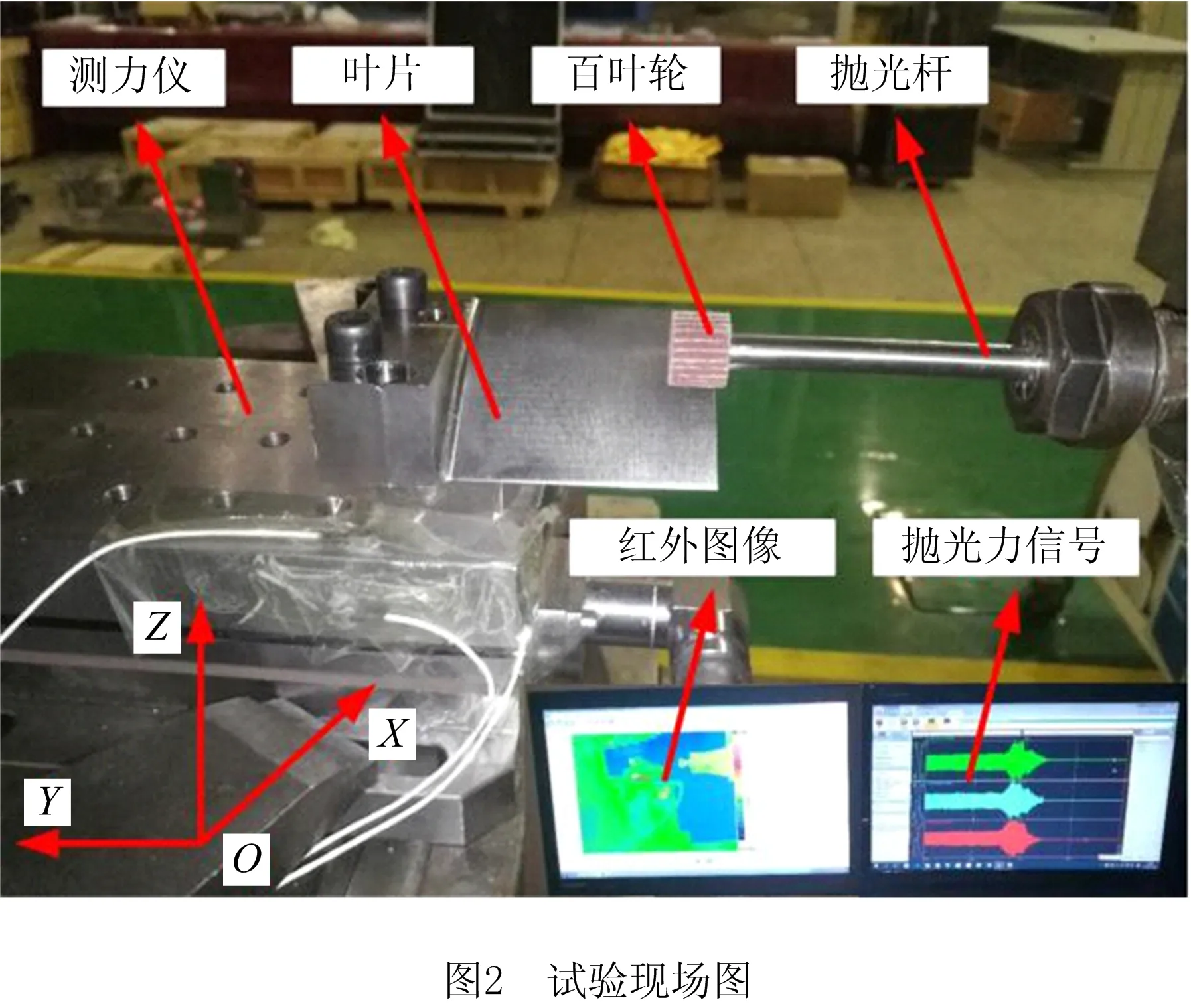
图2所示为试验现场，旋转的百叶轮在工件固定的情况下沿叶片表面的测地曲线横向运动，该抛光过程属于干式抛光。测力仪坐标系如图2左下角所示，图2右下方为计算机获得的抛光力信号和红外成像图片。

2 接触弧长的计算

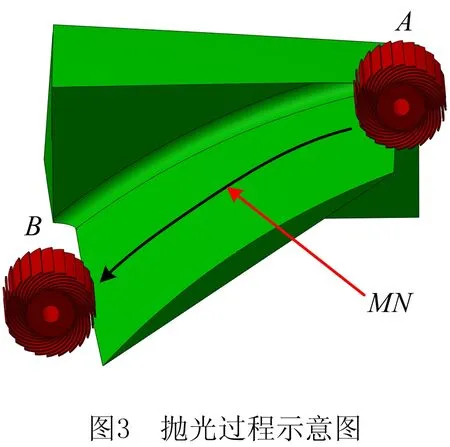
接触弧长的计算方法按文献[29-30]所述，在图3所示的抛光模型图中，叶片背面的曲线段MN为测地曲线，其长度为h。抛光路径为定向曲线段MN，属于横向抛光，垂直于MN的方向为纵向。如图3所示，位置A表示百叶轮刚开始接触叶片，该时刻记为t1，计算机采集软件上的抛光力信号开始变化(t1如图4)；当百叶轮移动到位置B时，标记为t2，表示百叶轮即将和叶片分离，抛光力信号开始返回到初始状态(t2如图4)。从t1～t2，总的抛光接触轨迹为接触弧长和MN长的总和，因此抛光过程中砂轮与叶片的接触弧长

l=vw(t2-t1)-h。

(1)

3 抛光力的坐标变换

以叶片为研究对象，FX和FZ分别表示测力仪测得的X和Z方向力，法向抛光力的方向是叶片表面接触面中心的法向。根据微分几何理论，因为图3中MN为测地线，其法线与曲面的法线重合，所以法向抛光力的方向是MN上抛光接触点的法向，切向抛光力的方向是MN上抛光接触点的切向。图5中的法向抛光力为Fn，切向抛光力为Ft，Ft和FX的夹角为β，根据力的合成与分解，

Ft=FXcosβ-FZsinβ，

(2)

Fn=FXsinβ+FZcosβ。

(3)

叶片曲面是非均匀有理B样条(Non Uniform Rational B-Spline，NURBS)曲面，MN是NURBS曲线。考虑到NURBS曲线在任意点可微，如果以N为原点建立坐标系x1Nz1，则MN的曲线函数表达式为

z1=f(x1)。

(4)

考虑到

tanβ=f′(x1)，

(5)

将式(5)代入式(2)和式(3)，可得：

Ft(x1,z1)=Fx(x1,z1)

(6)

(7)

法向力和切向力由式(6)和式(7)获得，抛光力则随图3中抛光轨迹MN上抛光点的改变而变化。图4中t1表示百叶轮刚切入工件的时刻，t2表示百叶轮切出工件的时刻，由图可知FX和FZ信号在切入和切出过程中波动较大，在MN中点附近波动较小，信号更稳定，因此以MN中点附近的抛光力作为测量结果。采用式(6)和式(7)计算MN中点附近的法向力和切向力，结果如表3所示。

4 抛光力模型的推导

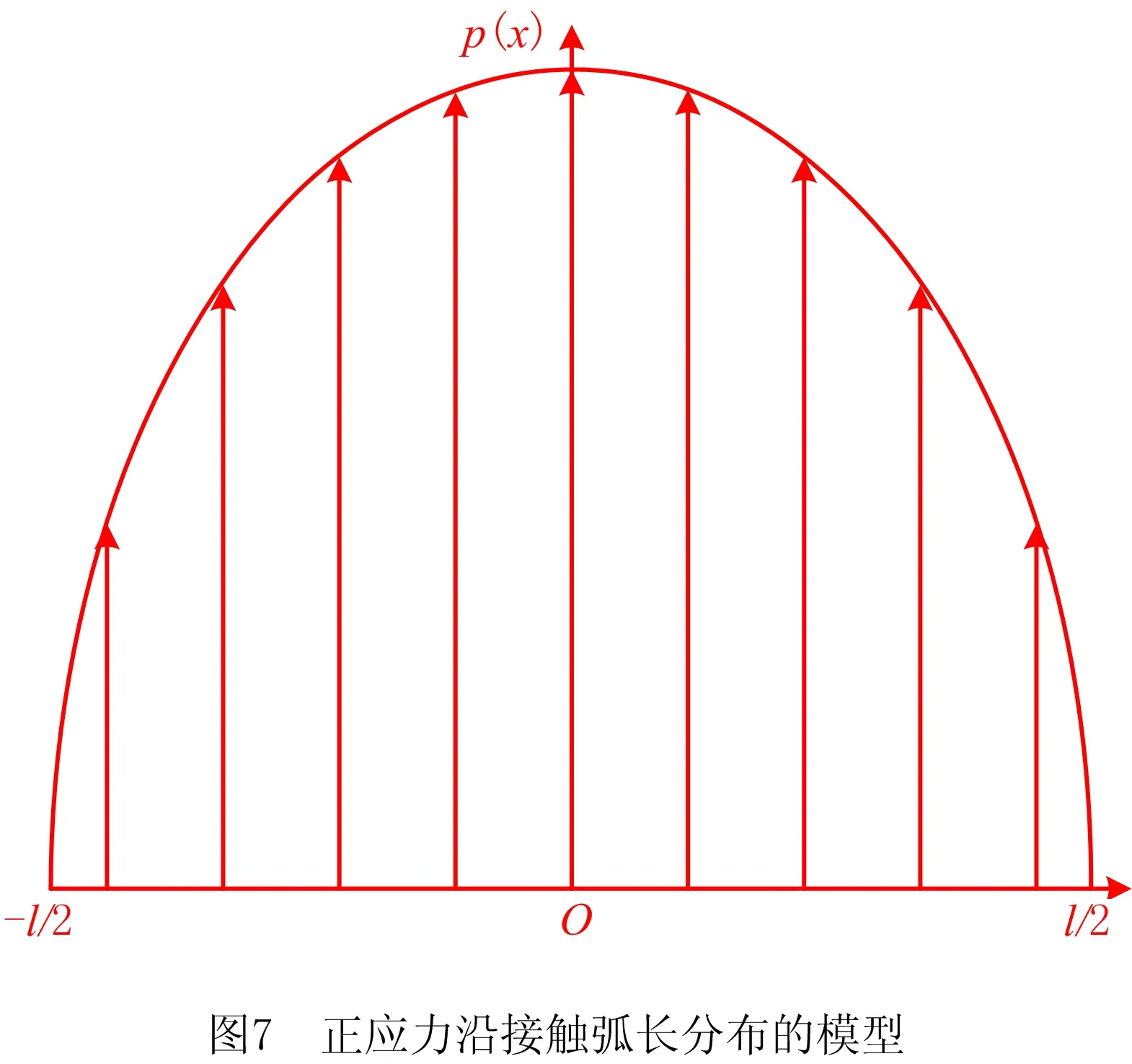
在抛光过程中，砂轮与叶片的接触区域近似为矩形ABCD，建立直角坐标系xoy如图6所示，l表示接触弧长，p(x)为正应力。

假设正应力与接触弧长之间的关系为椭圆函数(如图7)，则正应力

(8)

式中W为系数。

法向抛光力

Fn=p·S。

(9)

式中S为接触区域ABCD的面积。

图6中阴影部分表示微元接触面积，依图可知其表达式为

dS=b·dx。

(10)

式中：b为百叶轮宽度；dS为微元面积；dl为微元接触弧长。则微元法向抛光力可以表示为

dFn=p(x)·dS，

(11)

进而法向抛光力可表示为

(12)

将式(8)和式(10)代入式(12)，可得

(13)

根据定积分计算公式将式(13)化简为

(14)

引入系数k，令

(15)

则式(17)变为

Fn=kl，

(16)

切向抛光力也可以表示为

Ft=ktl。

(17)

式中kt为切向抛光力系数。

将表3的实验结果与模型结合，借助Minitab软件进行模型拟合得到模型系数。本实验中抛光轨迹中点的力模型可解为：

Fn=0.540 089l；

(18)

Ft=0.395 248l。

(19)

5 抛光温度的修正

抛光温度采用红外热成像检测系统进行测量，红外热成像检测系统可直接得到抛光过程中的红外热成像照片，采集频率为每秒50张照片，图8所示为采集到的热成像照片。

图8中砂轮与工件接触面的温度显示为50.76 ℃，因为红外成像仪中叶片的发射率设定为1，而实际物体的发射率小于1，所以该温度不是实际温度。为了获得真实的温度值，需要求解叶片的实际发射率。根据文献[31]，测量发射率的方法如下：

可以认为该红外成像仪为固定的发射率1，一般用其测量目标物的表面温度时，必须对测量显示结果进行修正后，才能较真实地反映被测目标物的实际温度。对于由测温仪固定发射率与被测目标物发射率不同而引起的读数误差，可以近似地用下式进行修正：

(20)

在试件表面的一半面积贴上黑胶带，胶带的发射率已知为0.93，将试件微微加热至大于室内温度，保温一段时间，然后将红外热像仪的发射率设置为0.93，先测量贴黑胶带处的真实温度为36.30 ℃，此时叶片显示的温度为28.54 ℃，由热传递可知，实际上贴黑胶带处的温度和试件温度应该一致，故θt=36.30 ℃，θn=28.54 ℃，εh=0.93，红外热像仪设置的测量波长为λ=(9.93±4) μm，将以上各值带入式(20)，求得叶片的发射率εb=0.89。

根据式(20)求图5中百叶轮与试件接触处的真实温度，此时θn=50.76 ℃，εh=1，求试件发射率为εb=0.89，λ=(9.93±4) μm，将各值带入得θt=59.71 ℃，该温度即为图9中工件和百叶轮接触处的实际温度，也就是图6中AD附近的温度，该温度减去环境温度便为测量点的温度升高值TΔ，如表3所示。

6 表面残余应力模型的建立

采用PROTO LXRD残余应力测试与分析系统对表面残余应力进行测试。为了确保与抛光力和温度测量点相同，残余应力测量点仍然选择为图3中抛光轨迹MN的中点。表面残余应力在平行于抛光轨迹的方向测量一次，在垂直于抛光轨迹的方向测量一次(如图9)，求其平均值如表3中的σ所示。本文的残余应力均指残余正应力(法向应力)，负值表示残余压应力，正值表示残余拉应力。

一般认为，残余应力由加工过程的机械作用、热作用和力热耦合效应共同造成，因此认为残余应力可以表达为这3项影响因素的叠加，即

σ=k1Fn+k2TΔ+k3FnTΔ+c。

(21)

式中：ki(i=1,2,3)为模型系数；c为常数项，因为所去除的表面材料为微米级，所以表达式中存在一个常数项，表示抛光前残余应力对抛光后残余应力的影响；第1项表示机械效应，第2项表示热效应，第3项表示热—机械耦合效应。

根据表3的测量结果，用最小二乘法可以求得表面残余应力模型表达式为

σ=-8.047Fn+4.76TΔ+

0.303FnTΔ-1 285.73。

(22)

式中：抛光力系数为负，说明抛光力会导致工件表面产生残余压应力；抛光温度系数为正，说明抛光温度会导致工件表面产生残余拉应力；第3项系数为正，意味着热—机械耦合效应将导致残余拉应力。这与以前学者的研究结论一致。抛光之前的叶片型面由球头铣刀铣削而成，测量铣削后的表面残余应力为-1 150 MPa左右，故抛光前的初始残余应力为-1 150 MPa，与模型中的常数项相差不大，可以认为常数项表示抛光前的初始残余应力。

根据传热学理论和Jaeger[32]提出的磨削温度场假设，百叶轮抛光叶片的过程可以看作为一个移动热源作用于叶片的过程。在不同时刻，工件的温度场分布不同，这是一个瞬态热传导问题。在解域Ω中，笛卡尔坐标系下的温度场微分方程为

(23)

近几十年来，许多学者对磨削传热问题进行了研究，Jaeger[32]提出的矩形移动热源模型已被广泛应用于解决许多实际问题。在矩形移动热源模型中，假设热源以工件速度vw沿半无限物体表面移动，鉴于抛光去除量为几十微米，忽略磨削深度的影响，认为加工面与未加工面重合，热源表面与其运动方向平行，如图10所示。

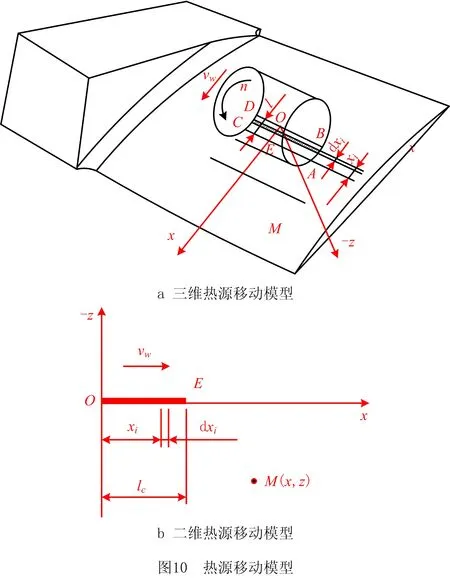
根据该模型可以求解微分方程(23)，得到整个热源对M点的温度升高值为

(24)

式(24)的被积函数很复杂，为了简化计算，本文只研究了沿x轴分布的表面温度(z=0)，因此式(24)可简化为

(25)

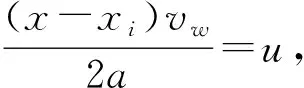
(26)

考虑到α=acρ,式(26)变为

(27)

式(27)中的被积函数是一个特殊函数，其标准形式为

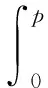
(28)

其函数值可以通过查表获得。

零阶二阶修正贝塞尔函数是一个对称函数，即K0[u]=K0[-u]=K0(|u|)，因此式(27)变为

(29)

当x=0时，图10中O点的温升为

(30)

根据Rowe[33]的热量分配系数模型，模型表达式为

(31)

式中ro为磨料颗粒的有效半径，通常等于表4所示筛孔直径的10%。

表4 不同粒度砂布轮对应的筛径

抛光过程产生的总热流密度

(32)

将式(18)、式(30)～式(32)代入式(22)，表面残余应力模型可表示为

(33)

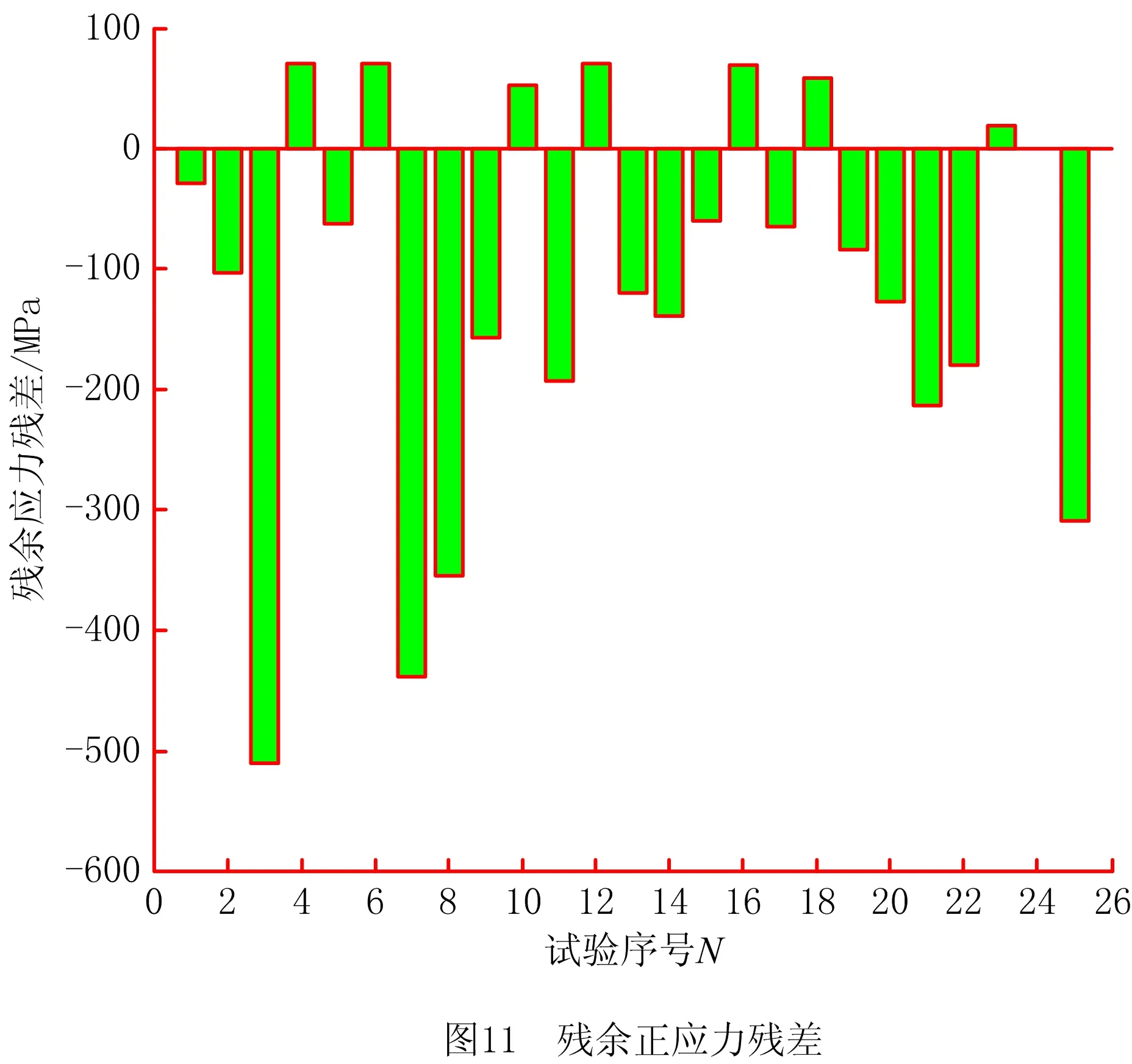
由式(33)得到的残余应力残差如图11所示，可见残余应力残差大多小于300 MPa，第3组和第7组工艺参数加工产生的残余正应力残差的绝对值大于400 MPa，这是由于第3组和第7组的主轴转速为4 000 r/min，压缩量为1.4 mm，该压缩量已经大于百叶轮在该转速下的增量，使抛光过程变为刚性抛光过程，而百叶轮粒度为240#，其磨粒较大，导致抛光力比其他组大得多，抛光温度自然也大得多，因为表面残余应力的主要影响因素为抛光力和抛光温升，所以这2组残差较大。由于残余压应力的基值均大于1 000 MPa，可以认为残余误差较小。

7 试验验证

根据实际抛光经验，选择合适的工艺参数对所建立的式(33)的模型进行验证，结果如表5所示。预测值和实测值的对比如图12所示。

表5 试验验证的测量结果

续表5

由图12可知，残余应力预测值和实测值的最大偏差率为11.09%，偏差值为147.72 MPa，而PROTO LXRD残余应力测试与分析系统测得的残余应力误差值为±50 MPa左右，残余压应力的实际值均在1 000 MPa左右，因此该模型具有较高的预测精度，理论预测结果与实验结果无显著差异，表明模型预测结果与实验结果吻合。

8 结束语

残余应力对零件的强度、硬度和稳定性等物理化学特性有重要影响，其研究对改善零部件性能有非常重要的价值。本文基于残余应力的产生主要源于力效应、热效应和力热耦合效应，建立了残余应力的简单数学模型。由表面残余应力模型(22)可知，力效应将产生残余压应力，热效应和力热耦合效应将产生残余拉应力，经过推导得到的残余应力模型仅与接触弧长、进给速度和百叶轮线速度3个因素有关。与已有模型相比，表面残余应力模型(33)虽然简单有效，预测准确性较高，但是在百叶轮压缩量大于百叶轮半径增量时，抛光过程变为刚性抛光，而且百叶轮粒度较小时的抛光力抛光温度急剧增大，其预测准确性变差。本文实验的抛光力大多小于10 N，叶片回弹效应可以忽略，当抛光力大于10 N时，残余应力模型已不再适用，需要建立新的模型，这将是未来的研究方向。