基于工件特征的曲面生成优化方法

李学兵，胡天亮+，刘忠强，马嵩华

(1.山东大学 机械工程学院，山东 济南 250061；2.高效洁净机械制造教育部重点实验室(山东大学)，山东 济南 250061；3.机械工程国家级实验教学示范中心(山东大学)，山东 济南 250061；4.山东大学 深圳研究院,广东 深圳 518000)

1 问题的提出

随着三维扫描设备的发展，点云获取技术越发成熟，成本越来越低，三维点云在逆向工程及工业测量等领域的应用越来越广泛[1-2]。逆向工程可应用于工件的产品改型设计、质量分析检测等领域以提高生产效率[3]，然而常用的三维点云是散乱三维点的集合，不存在任何拓扑关系，不能很好地表达工件的形状尺寸等信息。为更好表达工件外形特征和尺寸，点云数据需要进行曲面生成来构造出易于逆向和测量的网格模型。

在从点云到生成曲面模型的过程中，法向量估计和基于法向量的曲面重建是最基本的两个环节，国内外对此进行了一系列研究，具体如下：

(1)法向量估计 曲面重建算法依赖法向量估计与调整得到的法向信息，其结果直接关系曲面重建的成败。目前，根据法向量估计方法原理的不同主要分为基于局部表面拟合的方法和基于Delaunay/Voronoi的方法[4]。基于Delaunay/Voronoi的法向量估计方法计算效率低、耗费内存大，且容易受离群噪声点影响导致计算精度差，不适合处理诸如CAD模型等含有尖锐特征区域的点云数据。QUENTIN等[5]提出VCM (Voronoi covariance measure)算法，该算法较为复杂且计算效率较低。在基于局部表面拟合的法向量估计方法方面，HOPPE等[6]通过求取给定点的K邻域来拟合切平面，将该切平面的法向量作为点云表面该点的法向量，该方法虽然在尖锐特征处的估计精度偏低，但是算法效率高、性能稳定，对后续的贪婪投影三角化曲面重建算法影响不大，能够满足需要；CAZALS等[7]提出对K邻域进行Jet拟合的方法，Jet指截断的泰勒展开式，包含法向量、曲率等局部几何特征，相对于主成分分析(Principal Components Analysis, PCA)方法，该方法在高曲率处的计算精度有所提升，但是计算比较复杂。另外，法向量的指向往往不一致，导致法向量估计得到的结果存在二义性，需要进行调整。最小生成树法[8]是目前使用比较广泛的法向量调整算法，该算法调整一个点时需要遍历所有点，因此计算效率较低。针对特征简单的工件，本文提出效率较高的法向量调整算法。

(2)曲面重建 随着点云处理技术的成熟，曲面重建技术得到快速发展[9-10]。曲面重建的早期研究主要集中于显式重建，显式重建将整体点云数据的子集作为顶点，对顶点进行插值生成三角形，然后对点云进行三角剖分得到重建的曲面[11-13]；隐式重建也是三维点云曲面重建的重要内容，泊松重建就是经典的隐式重建算法，KAZHDAN等[14-15]和HOPPE等[16]提出泊松重建算法并不断进行改进，该算法通过对点云进行插值处理得到近似曲面。显式和隐式曲面重建的对比如表1所示。

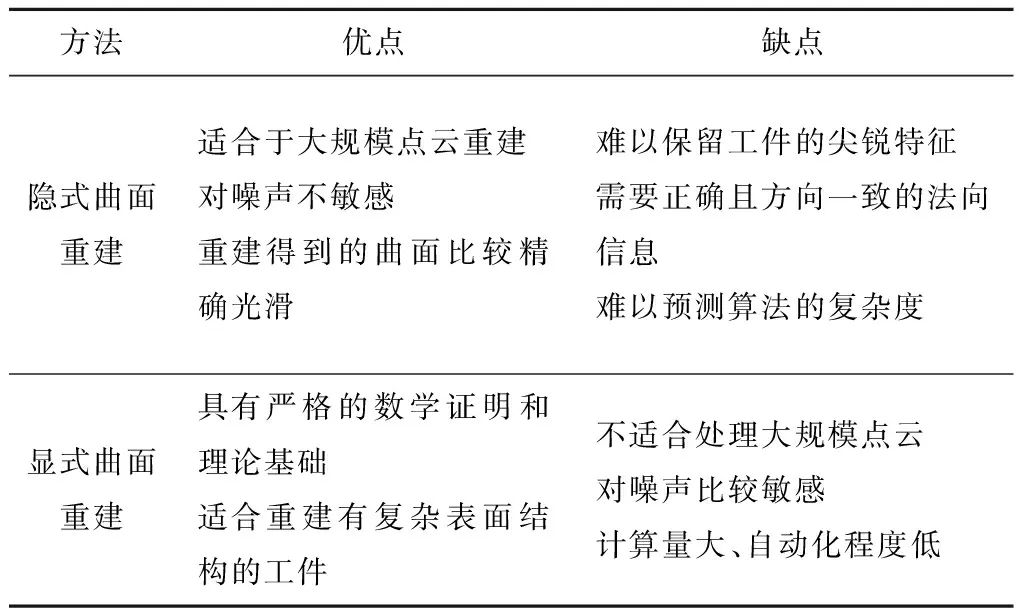
表1 隐式与显式曲面重建对比

针对法向量估计与调整计算效率较低的问题，本文采用PCA方法求取点云的法向量，并提出一种基于广度优先搜索的法向量调整算法，以得到正确的法向信息，为后续的曲面重建算法提供保证。在曲面重建方面，显式曲面重建算法适用于重建尖锐特征，在平缓特征处表现不佳；隐式曲面重建算法适用于重建光滑曲面，但是会使工件的尖锐特征变得光滑。针对这一问题，本文基于工件特征并充分结合显式和隐式曲面重建的优缺点开展研究，以得到更优的曲面重建方法。

2 曲面生成整体思路

综合分析隐式和显式曲面重建的优缺点可知，现有曲面重建方法各有所长，没有一种普适性的通用算法。工业应用中的工件形态千差万别，但是其表面特征却只分为曲面变分较小的平缓特征和曲面变分较大的尖锐特征两种。针对不同的特征，用同一种曲面重建算法必然效果不佳，因此本文结合工件特征提出一种曲面重建优化方法，以提高点云重建的精度。

本文用结构简单的常见工件为研究对象，对所提方法进行论述，其设计图纸如图1a所示。算法流程是首先使用三维扫描设备获取工件的点云数据，然后对点云进行一系列处理，最终得到工件的曲面模型，如图1b所示。

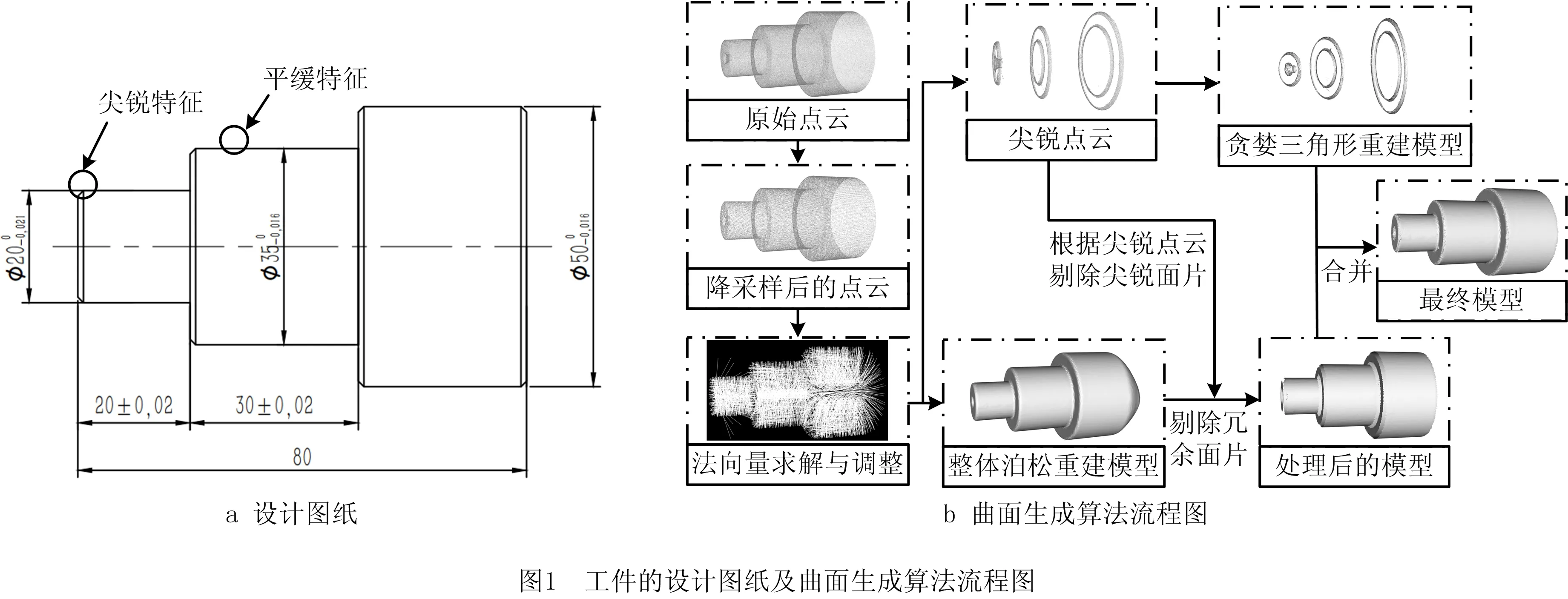
首先通过对点云进行降采样来减少点云数据；然后求取工件表面每个点的法向量，调整法向量的方向指向工件一侧，并根据曲面变分从点云中区分出尖锐部分；接着对尖锐部分的点云进行贪婪投影三角形重建，对整体点云进行泊松重建，并根据整体和尖锐点云剔除冗余和尖锐部分的三角面片；最后将两部分三角面片合并，得到最终的曲面模型。

3 点云数据获取及其预处理

3.1 点云数据获取

点云获取方法主要分为接触式和非接触式两种。接触式采集主要用三坐标机在工件表面采点，其测量精度较高，但是测量时间长、成本高，获得的数据点少，不能满足高精度三维重建的需要；非接触式采集主要包括三维结构光测量、激光测量等，其因测量速度快、成本低且能获得大量数据点而广泛应用于工业界。

本文点云均通过如图2所示的基于双目结构光的三维扫描设备获得，双目相机为大恒DH-HV1351UM，镜头为16 mm焦距，投影仪分辨率为1 920×1 280。

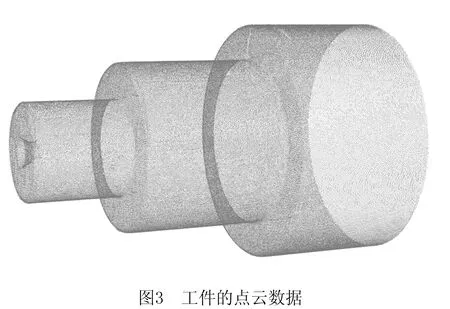
通过三维扫描设备采集的点云数据如图3所示，因为工件底部与工作台表面接触，无法被扫描到，所以得到的是一个非封闭点云数据，本文以该数据为研究对象对所提方法进行论述。

3.2 点云数据降采样

通常点云数据中包含的数据点数高达几十万个，这将会在后续操作中大大降低点云的处理速度，因此需要对原始点云进行降采样以减少数据量，目前比较常用的是基于体素网格的降采样方法[17]。首先将点云数据划分为三维体素网格，然后计算网格内所有点的重心，用于代替网格内的所有点。假设某网格内的所有数据点组成的集合为{Pi},i∈{1,2,…,n}，n为该网格内数据点的个数，则该网格的重心

(1)

该方法充分考虑了点云的空间特征，可以在保证点云所含信息基本不变的情况下，大大减少点云的数据量，提高后续算法操作的效率。

3.3 点云法向量估计与调整

法向量估计是点云处理过程中重要的一步，目前有多种点云法向量估计算法[8,18]，其中PCA适用于处理扫描工件得到的稠密点云。法向量估计与调整方法如图4所示。

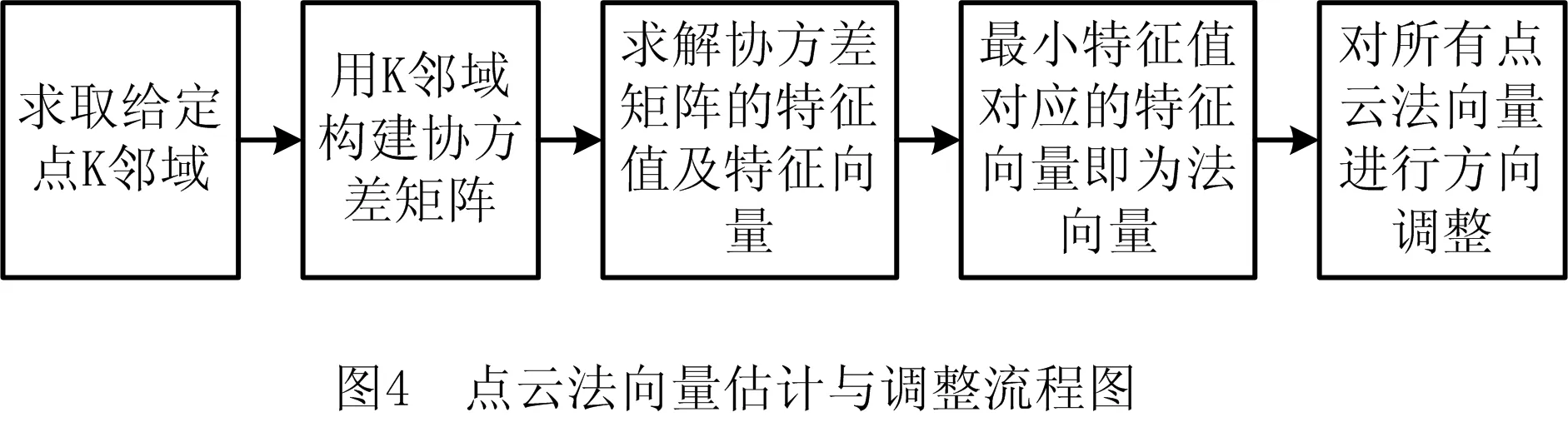
整体思路为求取给定点的K邻域，用K邻域拟合一个平面，将平面的法向量作为该点的法向量[6]。首先从所有数据点中求出距离给定点最近的k个点作为该点的K邻域，k的大小可根据实际数据及不同应用场景进行调整；然后根据这k个点构建协方差矩阵，并求解该矩阵的特征值和特征向量；最后用广度优先的策略遍历所有点，并在遍历过程中调整法向量方向，使其指向一致。

3.3.1K近邻求解

3.3.2 协方差矩阵的构建求解

三维点云共有3个坐标，即有3个随机变量x,y,z，3个随机变量自由组合可得协方差矩阵

Cov(x,y,z)=

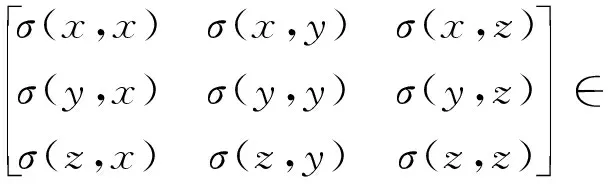
(2)

求得特征根λi和特征向量υi，对特征根进行排序，有λ0<λ1<λ2,λ0对应的法向量υ0为切平面的法向，即该点的法向量。

该点处的曲面变分[19]

(3)

式中λ0,λ1,λ2为给定点沿对应特征法向的偏移量，类似于用曲率描述曲面的微分性质，可用其衡量点云的局部微分性质，即衡量点云的平缓程度。

3.3.3 法向量调整

法向量估计之后，一部分法向量指向工件外侧，一部分指向工件内侧，法向量指向不一致将导致泊松重建失败，因此必须对所有法向量进行调整，使其指向工件一侧。

本文提出一种基于队列的广度优先算法，能够在搜索过程中不断调整法向量，有较高的计算效率，算法流程图如图5所示。算法通过判断向量相乘是否为正来调整法向量，假设给定点的法向量为ni,待调整的点的法向量为nj，若ni·nj>0，则两个法向量共向，不做调整；若ni·nj<0,则两个法向量异向，反转nj。遍历方法则是选取一点作为法向量调整的起始点，从起始点开始采用广度优先策略向整个点云扩展，在扩展过程中完成对法向量的调整。从最终的法向量估计结果来看，该方法能够正确高效地求解点云法向，为后续的曲面重建提供保障。

4 基于工件特征的曲面重建优化

本文重点研究显式重建中的贪婪投影三角形重建算法和隐式重建中的泊松重建算法，分别对工件的平缓和尖锐特征进行重建，最终得到精度较高的曲面模型。

4.1 贪婪投影三角形和泊松重建

贪婪投影三角形算法是一种基于贪婪算法的网格曲面重建算法；泊松重建算法是一种经典的隐式曲面重建算法，其通过将曲面重建转化为泊松方程来求解问题，该算法要求点云的法向量一致且朝向统一指向工件外侧或内侧，如果法向量缺失或指向不统一，则重建效果不好，甚至导致失败。

4.2 算法优化方案

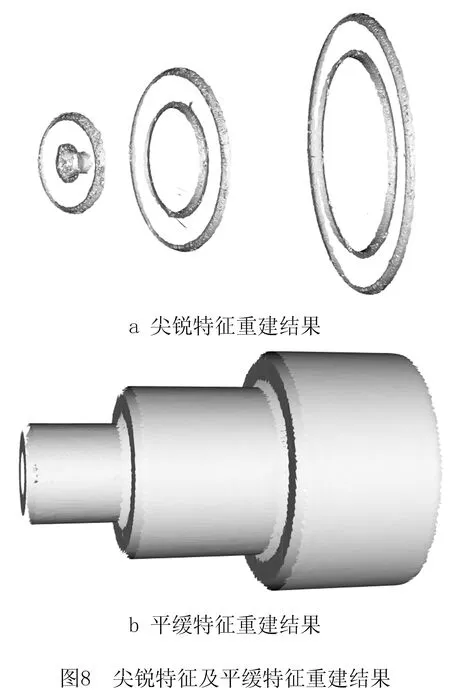
图6所示为采用两种算法重建的结果，其中泊松重建得到曲面模型，重建后的尖锐特征变得比较光滑；通过贪婪投影三角形重建算法得到曲面模型，虽然保留了棱角处的尖锐特征，但是平缓特征没有泊松重建得到的曲面精确光滑。

贪婪投影三角形算法对尖锐和平缓特征的重建效果没有明显区别，而泊松算法在平缓处的重建效果很好，在尖锐处却很差，因此本文对二者各取所长。整体点云采用泊松重建剔除尖锐特征和冗余的三角面片，仅保留平缓处的曲面模型，尖锐特征处的点云采用贪婪投影三角形重建，最后将二者重建的结果合并，得到工件最终的曲面模型。

4.3 尖锐特征处理

工件平缓特征的曲面变分较小，尖锐特征的曲面变分较大，根据第3章法向量估计时得到的曲面变分，可以很容易地区分尖锐特征和平缓特征。

实践发现，用式(4)定义分割阈值能够更精确地定义平缓和尖锐特征。

(4)

式中：m为比例因子，默认为1便可有效区分平缓和尖锐特征，而且通过调整m值可以区分得更精确;n为数据点的个数。

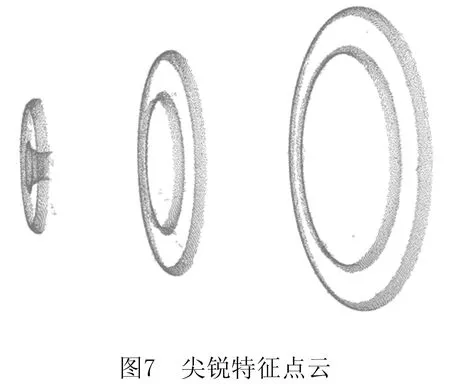
数据点的曲面变分大于T则为尖锐特征，小于T则为平缓特征，最终提取出的尖锐特征如图7所示。

5 实验结果分析

5.1 kd树算法效率分析

由于用点云数据构造kd树可以提高近邻求取等后续算法的效率，现以阶梯轴的点云数据(k=18)为例分别基于数组和kd树测试求取近邻及后续操作所需的时间，结果如表2所示。可见，对于大规模点云，基于数组的算法效率过低，甚至无法满足实际需要，kd树则大大提高了点云处理的效率。

表2 kd树与数组算法效率比较 s

5.2 法向量估计与调整结果分析

不同的法向量估计算法有不同的算法效率和性能，现针对常用工件对引言中提到的的法向量估计算法进行测试，所耗时间如表3所示，估计效果如图10～图12所示。

表3 法向量估计效率比较 s

根据实验结果可知，VCM算法耗费的时间最长，而且由于易受噪声影响导致图12中的阶梯台数据法向估计出现错误。PCA算法和Jet算法均为基于局部拟合的算法，由于工件尖锐处存在倒角，从结果来看二者估计的精度相当，但是PCA算法的效率比Jet算法更高。

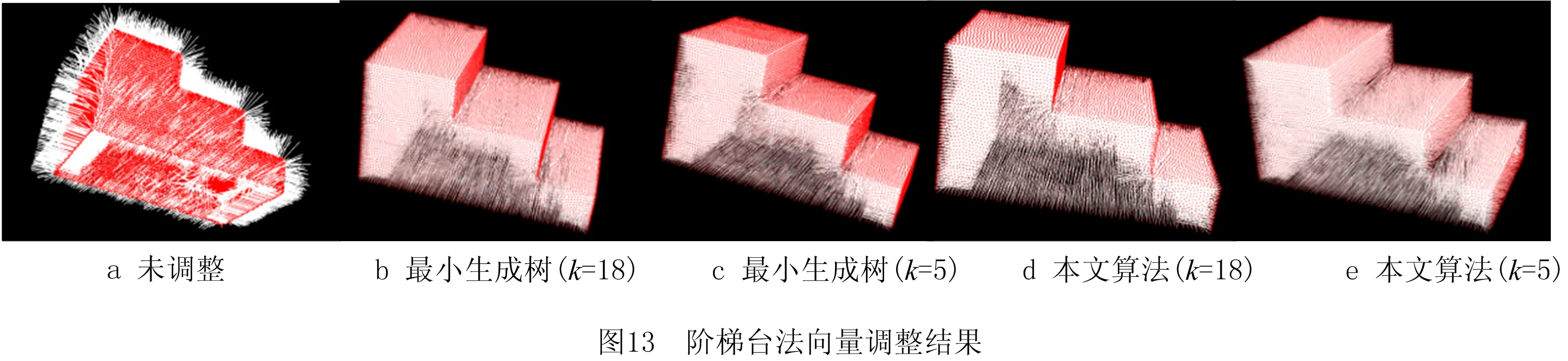
下面对法向调整的最小生成树算法和本文算法进行对比分析，所耗时间如表4所示，估计效果如图13和图14所示。

表4 法向量调整效率比较

从实验结果可以看出，本文算法与最小生成树算法均能正确调整法向。本文算法的效率明显高于最小生成树算法，但是因为本文算法仅针对结构简单的工件，未考虑形状复杂的情况，为提高算法效率进行了折中，所以没有最小生成树算法的应用范围广泛。

5.3 曲面重建结果分析

在逆向工程中，曲面拟合精度体现在原始数据和重建得到的曲面模型之间的偏差，一般采用原始点云到模型表面的距离来衡量。假设Dj表示点Pj到其模型表面的最小距离，则最大值为点云距离曲面模型的最大距离，如式(5)所示；均值为点云距离曲面模型的平均距离，用于表征曲面模型的整体精度，如式(6)所示；标准差为点云距离曲面模型的标准差，用于表征曲面模型精度的稳定性，如式(7)所示。

Dmax=max{Dj},j∈[1,n]；

(5)

(6)

(7)

式中n表示数据点的个数。采用上述标准对3种曲面重建算法得到的模型进行评估，结果如表5所示。

表5 阶梯轴曲面重建精度 mm

根据实验结果，本文算法的Dmax与另两种算法结果相近，表示合并后的模型中某一数据点距离其最近面片的最大距离，是整体数据点的一个极大值，对整体精度影响不大；Dstd较另两种算法有所下降，说明本文算法得到的模型与点云距离的离散程度更小，整体模型的稳定性更好；Dmean小于另两种算法，可知本文算法得到的曲面模型的整体精度最好。本文方法的重建效果如图15所示，相对于图6所示的重建效果也有所提升，然而由于两种曲面重建算法和合并算法本身的局限性，也可能会出现网格空洞和网格拼接错位等模型失真现象，业界针对这一问题已有比较成熟的解决方法，即将结果放到Geomagic Studio中修复。综上所述，本文算法结合工件特征吸取两种重建算法的优点，提高了曲面生成的整体精度。

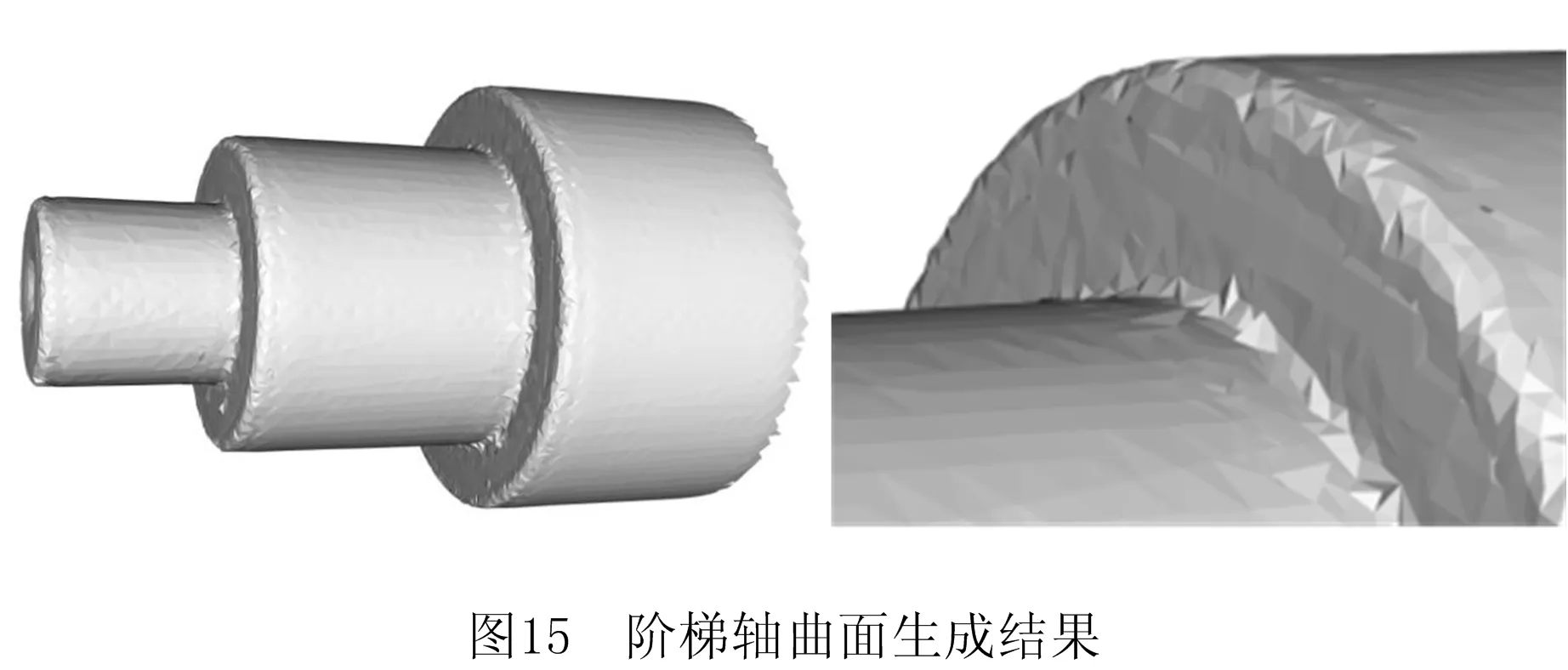
6 结束语

本文基于工件特征提出法向量估计及调整算法，并对曲面重建算法进行了优化。该算法首先通过降采样来降低点云数据的数据量，以提高后续操作的效率；然后采用PCA方法求取法向量，并根据广度优先策略调整方向，为曲面重建奠定了基础；接着通过泊松算法处理工件的平缓特征，通过贪婪投影三角形算法处理工件的尖锐特征，最后将两部分结果合并得到最终的曲面模型。实验表明，相比以上两种算法，本文所提算法在精度上均有所提升，为曲面重建算法在工件的逆向及测量领域的优化提供了借鉴。未来将重点研究网格空洞和网格拼接错位的修复问题，以进一步提高本文算法的鲁棒性和稳定性。