基于用户偏好和麻雀搜索聚类的协同过滤算法

聂晓明 高鹏翔

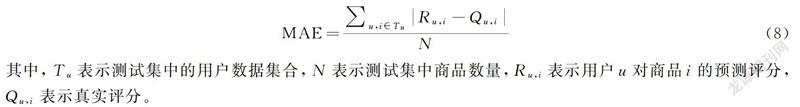
摘要：针对推荐算法数据稀疏及聚类中心点敏感问题，提出了一种基于用户偏好和麻雀搜索聚类的协同过滤推荐算法。首先使用评分偏好模型对原用户项目矩阵进行修正，得到新的用户偏好-项目矩阵。利用麻雀搜索对聚类中心点进行优化，从目标用户所在簇内得到最近邻，提高了算法迭代速度，改善了聚类中心点敏感的问题。使用相似度公式对目标用户未评分项目进行预测，并完成推荐。实验结果表明，相较于其他几种推荐算法，准确度提高了4到6个百分点。

关键词：评分偏好;麻雀搜索;协同过滤;推荐精度

中图分类号：TP391.3

文献标志码：A

文章编号：1006-1037（2021）01-0070-07

基金项目：

山东省自然科学基金（批准号：ZR2019PEE018）资助。

通信作者：高鹏翔，男，教授，主要研究方向为人工智能。E-mail：gappengxiang@qdu.edu.cn

近年来，随着网络信息数据的急剧增长，带来了大数据时代。随之而来的是用户的个性化需求不断提高，如何寻找到用户真正感兴趣的信息已经成为一项棘手的难题。为此，人们开发出了推荐系统[1] （Recommender Systems），根据不同用户的个性化需求，推荐用户最有可能喜欢的条目。推荐系统的技术核心是推荐算法，其中，协同过滤算法是推荐系统中应用最为广泛、最成功的技术之一。协同过滤算法的原理是试图通过对用户过去行为的了解，找出相似用户，分析相似用户喜欢的项目集合完成推荐项目。但是协同过滤算法存在一定的不足，如冷启动、稀疏性以及缺乏定制推荐[2]，仍需要对其不断完善。为了改善算法的推荐准确性，研究人员从不同的方面做了研究，针对矩阵稀疏的问题，Hu等[3]证明了聚类技术如何改进协同过滤算法并有效提高在稀疏矩阵中的推荐效果。Xiong等[4]利用统计学聚类算法，提出一种基于项目的协同过滤推荐系统，有效的解决了数据稀疏的问题。Xia等[5-6]提出了一种利用矩阵填充的协同过滤算法，通过算法模型对缺失的数据进行评分的预测填充，以此来缓解数据稀疏问题，但由于缺省值的设置导致误差的产生，预测的评分依然不够准确。Shi等[7]通过关联规则评估用户之间的相似性来解决这个问题。使用上述算法对相关联项目的权重进行分配和迭代改进，有效地提高了推荐的准确性。针对传统协同过滤推荐技术的冷启动问题，Zhou等[8]将基于人工鱼群聚类应用到基于用户的协同过滤推荐系统中，提高了推荐结果的准确率。赵亚辉等[9]利用用户之间的信任信息，更好地找到兴趣相似的用户集，增强推荐效果。林甲祥等[10]提出的结合社交关系和关联规则的推荐算法可以有效解决冷启动问题，但是算法实现过程较复杂，在实际应用中可能在于系统的吞吐量会受到限制。上述研究都在一定程度上提高了协同推荐算法的准确性，缓解了协同过滤算法中的问题。然而，这些方法都忽略了用户的评分偏好对结相似度计算带来的影响，以及在面临聚类时容易出现中心点敏感问题，导致最近邻居选取不准确，本文提出了一种基于用户偏好和麻雀搜索聚类的协同过滤算法（Collaborative filtering algorithm based on user preference and sparrow search clustering，UPSSCA-CF）。利用用户对评分的偏好属性修正用户—项目矩阵，使用麻雀搜索的聚类算法，对修正后的用户偏好—项目矩阵进行聚类分组，在目标用户的所属类簇中，通过相似度和评分预测公式对矩阵中缺失的项目值进行填充，找出目标用户未评分项目中最高的N个项目，从而完成推荐。通过在MovieLens数据集上进行实验验证。

1 传统的基于聚类协同过滤算法

聚类算法的思想引入推荐系统中，可以很好的找到用户之间的相似关系。聚类问题[11-12]可以定义为：给定的n维用户行为矩阵中对用户进行聚类，计算并比较目标用户与预设定的k个中心点之间的距离，将行为相近的用户点划分到同个簇中，然后从距离最近的k个簇内生成最近邻居集[13]。

（1）产生用户—项目评分矩阵。假设对项目进行评分的用户的id集合为U=ui|i∈1，2，…，n，和项目的id集合为i=it|t∈1，2，…，m。用户对项目的评分矩阵用R=Ri，j|i∈1，2，…，n，j∈1，2，…，m表示，其中元素Ri，j表示ui对项目ij的评分，其范围为1到5之间的整数。

（2）计算用户的相似度。用户相似度计算是协同过滤中的关键环节，需要计算每个用户和其他用户之间的相似度。目前应用最广泛的相似度计算方法有Pearson相似系数、Jaccard相似系数和余弦相似系数[14]等。本文选择用来计算相似度的是Pearson相似系数

其中，simu，v表示用户u和用户v的Pearson相似度，items表示用户u和用户v的共同评分项集合，Ru，i和Rv，i分别表示用户u和用户v对项目i的评分分数，Ru 和Rv 分别表示用户u和用户v平均评分[15]。

（3）评分预测推荐。得出用户之间的相似度后，通常采用KNN推荐模型[16]进行最近邻集合的选取，从而进行评分预测，将需要推荐的项目与用户已购买的项目进行比较，在用户未进行评分的项目中，把预测评分最高的n个项目推荐给目标用户

其中，Ru，i表示用户u对产品i的预测评分，SUser表示用户的最近邻集合。simu，v表示用户u和用户v的相似度，Ru、Rv表示用户u和用户v对其他产品打分的均值[17]。

2 UPSSCA-CF

2.1 用户偏好—项目矩阵

考虑表1中的用户项目评分矩阵用户项目评分矩阵相似性矩阵假设，如果用户u1喜欢某个项目，则会打4分，相反如果不喜欢，则打1分。因此，从表1可以看出，u1喜欢i2，但不喜欢i1。但是如果其他用户u2喜欢i2和u1喜欢i2一样多，会给i2打5分。用户u2不喜欢i2，会将其评为2。因此，u1和u2之间的相似性應该是1，因为他们都喜欢i2不喜欢i1，但显然通过公式求出两者的相似性矩阵中的值却不是1。这种矛盾的发生是因为用户对物品的打分习惯是存在差异的[18]。

为此本文使用用户打分偏好来对用户—项目矩阵进行修正。引入评分偏好模型[19]，假设评分类别集合为P1，…，P5，若Pj<Pi，表示评分类别Pj小于评分类别Pi。用户u对评分类别的偏好得分

计算出所有用户的评分类别偏好后，使用用户评分类别偏好得分代替用户—物品矩阵中的原始得分，得到修正后的用户偏好—项目矩阵，该矩阵元素的值代表用户对物品的偏好，在一定程度上提高推荐准确率。

2.2 麻雀搜索聚类的协同过滤算法

本文对上一节得到的用户偏好—项目矩阵使用麻雀搜索优化K-means算法的中心点的选择，改善了聚类算法中心点选取敏感问题，增强了聚类效果并提高了推荐算法的可扩展性。该矩阵可表示为X=x1，x2，…，xi，…，xn ，其中xi表示用戶ui对所有项目类型的偏好。

2.2.1 麻雀搜索算法 麻雀搜索算法[20]是一种新型的群智能优化算法，受麻雀的觅食行为和反捕食行为的启发，模拟了麻雀群觅食的过程。麻雀中负责寻找食物并为整个麻雀种群提供觅食区域和方向的个体作为发现者，其他麻雀作为跟随者，跟随者则是利用发现者来获取食物。同时还叠加了侦查预警机制，种群中选取一定比例的麻雀进行侦查预警，监视群体中其它麻雀的危险行为，该种群中的攻击者会与高摄取量的同伴争夺食物资源，如果发现危险则放弃食物，以提高自己的捕食率。

发现者通常有高水平的能量储备，并为所有的觅食者提供觅食区域或方向，负责确定可以找到丰富食物来源的地区。能量储备水平取决于对麻雀健康值的评估。一旦麻雀发现了捕食者，就会发出警报信号。当报警值大于安全阈值时，发现者需要将所有麻雀引向安全区域。每代发现者的位置更新

其中，t表示当前迭代，j=1，2，…，d，Xti，j表示种群中第t代中第i个麻雀的第j维位置，itermax是迭代次数最多的常数。α∈（0，1]是一个随机数，R2R2∈[0，1]和STST∈[0.5，1]分别代表报警值和安全阈值，Q为一个标准正态分布随机数。当R2<ST时，说明周围没有捕食者，生产者进入广域搜索模式。如果R2≥ST，说明一些麻雀已经发现了捕食者，所有的麻雀都需要迅速飞到其他安全区域。

对于跟随者，一些跟随者会频繁地监视生产者。一旦发现生产者找到了好的食物，会立即离开现在的位置去竞争食物。如果赢了，可以立即得到生产者的食物，否则，将继续执行跟随能提供最好食物的生产者去寻找食物。跟随者的位置更新公式

其中，Xt+1P是生产者占据的最佳位置;Xtworst表示当前全局最差位置;A表示1×d的矩阵，其中每个元素随机分配1或-1，并且A+=ATAAT-1。当i>n/2时，说明适应值较差的第i个跟随者最有可能饿死。

麻雀觅食的同时部分麻雀负责警戒，当危险靠近时，麻雀会放弃当前的食物，即无论该麻雀是发现者还是跟随者，都将放弃当前的食物而移动到一个新的位置。每代将从种群中随机选择Sn个个体进行预警行为。其位置更新公式

其中，Xtbest是当前的全局最优位置;β是步长控制参数，取值是平均值为0、方差为1的随机数的正态分布;K∈-1，1是一个随机数表示麻雀移动的方向，也是步长控制系数;fi是目前麻雀的适应值，fg和fworst分别是当前的全局最佳适应值和最差适应值，ε是最小常数，以避免零除误差。当fi≠fg表示麻雀位于簇的边缘。Xtbest显示了聚类中心的位置，周围是安全的。fi=fg表明，处于种群中间的麻雀意识到了危险，需要靠近其他麻雀。

2.2.2 麻雀搜索的用户聚类算法 融合麻雀搜索的用户聚类算法（User clustering algorithm for sparrow search，SSCA）的算法思想是先利用麻雀搜索算法查找最优的初始聚类中心，再使用最优的初始聚类中心对用户进行K-means聚类。麻雀搜索算法中的每一只麻雀表示一个聚类中心矩阵C=C1，C2，…，Cc，在麻雀搜索算法中，每只麻雀有一个位置属性，代表找到的食物的位置，在D维解空间内每只麻雀的位置为适应度值，所有麻雀的适应值可以用以下向量表示

其中，D表示麻雀的数量，每代选取种群中位置最好的Pm只麻雀作为发现者，剩余的D-Pm只麻雀作为跟随者。Fx中每行的值表示个体的适应值。在SSCA算法，具有较好适应值的生产者在搜索过程中优先获得食物，见算法1。

2.3 UPSSCA-CF算法流程

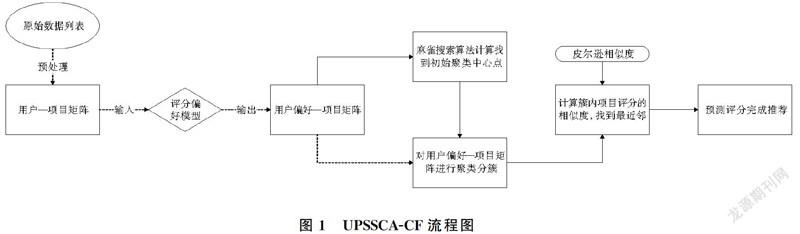
UPSSCA-CF分为以下5步，具体流程如1图所示。

（1） 首先对原始数据列表进行预处理，生成用户—项目矩阵。然后输入到评分偏好模型中，对每个用户的所有评分进行计算，计算得出用户的评分偏好得分，使用评分偏好代替原来矩阵的评分值，构建用户偏好—项目矩阵;

（2） 使用算法1，对用户偏好—项目矩阵中的每一个用户进行搜索，找到最优的位置，作为初始聚类的中心点;

（3） 对用户偏好—项目矩阵进行聚类，根据聚类结果将用户分成不同的簇，并找出目标用户所在的簇;

（4） 在目标用户所在簇中，使用式（1）计算相似度，并且按照降序进行排列，采用KNN推荐模型选取与目标用户最相似的k个用户作为最近邻集合;

（5） 在最近邻集合中，将需要推荐的项目与用户已购买的项目进行比较，将从用户未使用过或未购买过的项目中，使用式（2）对项目评分预测，把预测评分最高的n个项目推荐给用户，完成推荐。

与主流的基于K-means聚类算法 （K-means）对比， UPSSCA-CF算法在聚类分簇之前，使用麻雀搜索算法寻找最优的初始中心点，优化算法，提高了算法应对聚类中心点敏感这一问题。与主流的粒子群优化的协同过滤算法（ParticleSwarmOptimization，PSO-CF）进行对比，UPSSCA-CF算法增加了评分偏好模型，通过用户的打分习惯偏好对矩阵进行修正得到用户偏好—项目矩阵，提高了推荐算法的准确性。

3 实验及结果

3.1 实验环境与数据集

本文的实验环境为一台PC机，机器的配置为intel core i5、1.60GHz、8GB，操作系统为windows10，实验使用Python实现。选取MovieLens数据集[21]测试算法准确性。MovieLens数据集是公认为评估推荐算法最主要的数据集之一，数据集的下载链接为http：//files.grouplens.org/datasets/movielens/。该数据集提供了几种不同数量级的数据，本文选取的是十万量级的数据集，包括近千个用户对1 682部带有标签的电影提供的评分记录，为方便推荐算法的使用，该数据集的评分范围为1～5分，1表示不喜欢，5表示很喜欢。该数据集可以使用的評分只占6.3%，是一种特别稀疏的数据集。本文通过对该数据集进行预处理，提取出用户对项目的评分保存在用户—项目评分矩阵中。

3.2 实验方法与度量标准

本文采用k折交叉验证，将研究数据分为k份，再将k份采用不同比例的分割进行交叉验证。文中k=5，即5折交叉验证。比如取出1份作为测试集，剩下的4份作为训练集。每个实验进行5次试验，最终对5次实验的值取平均值，进行比较分析。

为了验证推荐算法的推荐准确性，采用广泛应用于比较和测量推荐系统的标准，统计平均绝对误差（mean absolute error，MAE）度量标准。MAE是对所有测试用户对测试项目的预测评分和实际评分的平均误差大小的计算

其中，Tu表示测试集中的用户数据集合，N表示测试集中商品数量，Ru，i表示用户u对商品i的预测评分，Qu，i表示真实评分。

3.3 实验结果

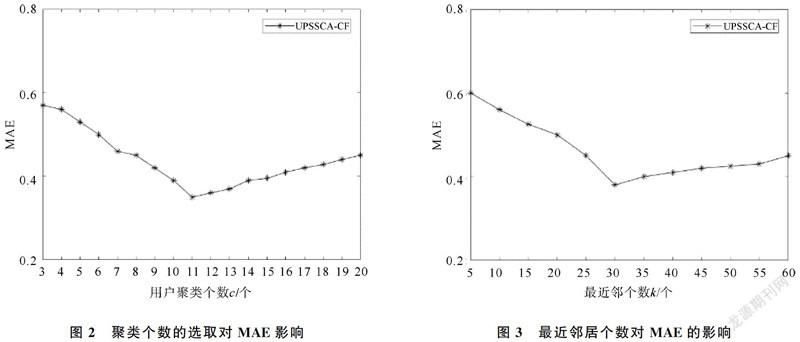
3.3.1 用户最佳聚类个数c的确定 为了确定用户的最佳聚类个数c，实验中c值的取值范围为[3，20]，选取最近邻居数量默认设置为20，其MAE结果如图2所示。可知，用户的聚类个数为11时，MAE值最小。因此，用户的最佳聚类个数为11。

3.3.2 用户的最佳近邻个数k的确定 本文实验中针对最佳邻居个数k值的取值进行限定，取值范围为（5～60），k取值的不同对MAE的影响如图3所示。可知，最近邻居个数k在[5，30]的范围内，MAE随着k的增加而呈现下降趋势，表明推荐效果在该范围内随着最近邻居个数的增加而增加，在k=30时，本文算法的MAE最小。而当最近邻居个数k在[30，60]范围内，随着k的增加，MAE呈现缓慢上升的趋势。因此，在所提算法中最近邻居个数k的最佳值为30。

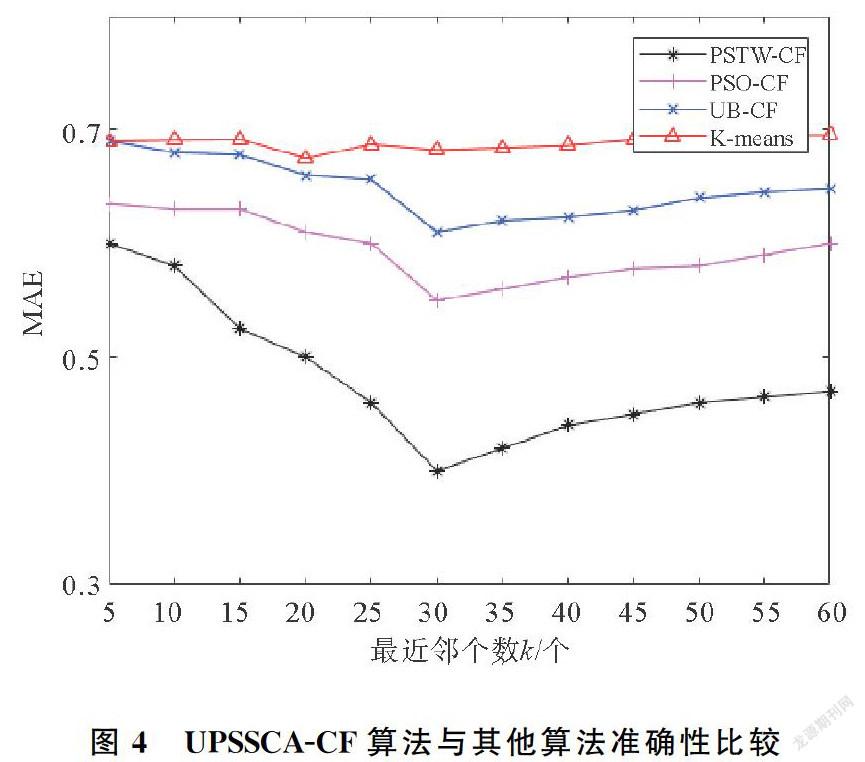
3.3.3 UPSSCA-CF与其他主流协同过滤算法的对比 为了验证本文所提UPSSCA-CF算法推荐结果的准确性，实验中选取了3种主流的推荐算法与其进行对比，包括基于K-means聚类算法 （K-means）、粒子群优化的协同过滤算法（ParticleSwarmOptimization，PSO-CF）和传统的基于用户的协同过滤推荐算法（UBCF）。参数的设置为：聚类的个数为11，最近邻个数的取值范围为（5～60）。实验结果如图4所示。

通过实验对比分析，本文算法与其他三种算法在不同的近邻数n下的实验结果，本文提出的算法取得MAE最小，即推荐结果的准确度最高。几种算法均使用聚类思想，但其余三种仅利用用户—项目评分矩阵，没有充分利用用户潜在信息，造成最近邻居选取不准确，降低了推荐结果的准确性。而本文充分利用用户自身的评分偏好形成用户偏好—项目矩阵，并在此基础上利用麻雀搜索的用户聚类算法进行聚类，增强了聚类效果，大大提高了最近邻选取的准确度。最后，使用用户相似度模型进行评分预测并做出推荐，进一步提高推荐结果准确性。

4 结论

本文提出的基于用户偏好和麻雀搜索聚类的协同过滤算法充分运用用户偏好的潜在信息，在预测阶段，改善了聚类过程初始聚类中心敏感的问题，大大降低算法的计算量，提高了在稀疏矩阵上预测的准确度。在推荐准确率上，UPSSCA-CF优于传统的基于用户的协同过滤算法和传统的基于聚类的协同过滤算法。本文算法虽然在一定程度上缓解了评分数据稀疏性对推荐结果的影响，但由于用户的兴趣爱好存在时间周期性，即同一用户对同一商品的评分在不同时间段是不一样的，下一步在改进算法时考虑用户兴趣随时间的偏移带来的影响，以提高推荐准确率。

参考文献

[1]XU H L， WU X， LI X D， et al. Comparison study of internet recommendation system[J].Journal of Software，2009，20（2）：350-362.

[2]DENG A， ZHU Y Y， SHI B. A collaborative filtering recommendation algorithm based on item rating prediction[J]. Journal of Software，2003，14（9）：1621-1628.

[3]HU X， LU H R， CHEN X， et al. K-means item clustering recommendation algorithm with initial clustering center optimized[J]. Journal of Air Force Radar Academy，2014（3）：203-207.

[4]XIONG Z Y， ZHANG FJ， ZHANG Y F. Item clustering recommendation algorithm based on particle swarm optimization[J]. Computer Engineering，2009，35（23）：178-180.

[5]XIA H. Research on recommendation algorithm of matrix factorization method based on mapReduce[J]. Applied Mechanics & Materials， 2014， 631-632：138-141.

[6]WU B， LOU Z Z， YE Y D. Co-regularized matrix factorization recommendation algorithm[J].Journal of Software，2018，29（9）：2681-2696.

[7]SHI J P， LI J， HE F Z. Diversity recommendation approach based on social relationship and user preference[J].Computer Science，2018，45（Z6）：423-427.

[8]ZHOU Y Q， XIE Z C. Improved artificial fish-school swarm algorithm for solving TSP[J]. Systems Engineering & Electronics， 2009， 31（6）：1458-1461.

[9]赵亚辉， 刘瑞. 基于评论的隐式社交关系在推荐系统中的应用[J]. 计算机应用研究， 2016， 33（6）：1628-1632.

[10] 林甲祥，高敏节，陈崇成，等.个性化旅游景点推荐中考虑约束的关联规则挖掘算法[J].福州大学学报（自然科学版），2019，47（3）：320-326.

[11] 王卫红，曾英杰.基于聚类和用户偏好的协同过滤推荐算法[J].计算机工程与应用， 2020，56（3）： 68-73.

[12] 王兴茂，张兴明，吴毅涛，等.基于启发式聚类模型和类别相似度的协同过滤推荐算法[J].电子学报，2016（7）：1708-1713.

[13] 李改，陈强，李磊.基于评分预测与排序预测的协同过滤推荐算法[J].电子学报，2017（12）：3070-3075.

[14] 吕诚.基于用户相似度的加权项目偏差SlopeOne协同过滤推荐算法[J].南昌大学学报（理科版），2014（4）：342-347.

[15] 郝雅娴，孙艳蕊.K-近邻矩阵分解推荐系统算法[J].小型微型计算机系统，2018，39（4）：755-758.

[16] 黄国言，李有超，高建培，等.基于项目属性的用户聚类协同过滤推荐算法[J].计算机工程与设计，2010，31（5）：1038-1041.

[17] 周超，孙英华，熊化峰，等.基于用户和项目双向聚类的协同过滤推荐算法[J].青岛大学学报（自然科学版），2018，31（1）：55-60.

[18] 孙兰兰.基于用户协同过滤的近邻选择算法[J].青岛大学学报（自然科学版），2018，31（2）：116-120.

[19] REN P.TV recommender system based on confidence user preferencemodel[J].Modern Electronic Technique，2014（16）：30-33.

[20] XUE J， SHEN B. A novel swarm intelligence optimization approach： sparrow search algorithm[J]. Systems ence & Control Engineering An Open Access Journal， 2020， 8（1）：22-34.

[21] 王穎，王欣，唐万梅.融合用户自然最近邻的协同过滤推荐算法[J].计算机工程与应用，2018，54（7）：77-83.